一種基于多光波干涉的高精度光相位量化方法與流程
本發明涉及通信技術領域,尤其涉及一種在光信號處理過程中實現高精度相位量化的方法。該方法主要用于對光信號相位進行量化,并可應于受噪聲影響而產生相位模糊的調相信號的再生,是一種能夠獲得更精確相位量化結果的方法,尤其涉及全光信號處理領域。
背景技術:
隨著社會信息化水平的不斷提高,信息量也在爆炸式增長,光通信系統所承載的傳輸壓力也隨之增大,利用全光的方法對光信號進行處理,可避免光電和電光轉換,滿足高速處理信號的需求。如今,全光信號處理在采樣、復數濾波、傅里葉變換等方面均有較多的研究,在全光模數轉換(ADC)方面的研究也更集中與光信號幅度的量化,而對全光量化光信號相位的量化方面的研究還有所欠缺。光相位量化作為全光模數轉換(ADC)的有力補充,可以彌補現有全光量化研究中相位量化的空白。
信號在傳輸過程中會受到噪聲的影響,對于目前通信系統中廣泛應用的相位調制格式信號,噪聲會帶來相位模糊的現象,進而增大信號誤碼率;同時,放大器(如摻鉺光纖放大器)作為光通信系統中必不可少器件,會引入放大的自發輻射噪聲,在放大信號的過程中將噪聲也一同放大,會對原本就相位模糊的信號帶來更加不利的影響。
針對上述問題,有研究者提出了解決方案。RadanSlavl′k等人研究發現,信號光與強泵浦光注入高非線性光纖中通過四波混頻能夠產生各階相位諧波,通過選擇其中特定階次的相位諧波通過新的四波混頻過程與信號進行干涉,可實現相位量化,但其量化結果的精度還有待提高。由于參與干涉光波之間的功率比對量化精度有一定影響,Radan Slavl′k等人又研究了量化不同階次信號時需要的相位諧波以及諧波與信號的最優功率比。Parmigiani F等人針對相位量化過程中,在原始信號頻率處新產生的信號的強度不易控制,進而在兩者干涉時無法達到最優的相位量化結果的問題(即解決實際中如何實現最優功率比的問題),提出了解決方案。利用正 交的泵浦產生簡并正交的信號閑頻組,再通過偏振控制器調節信號和閑頻在X-Y平面的角度,使其發生干涉,進行相位量化。但是該方法在實現相位量化的時候,由于信號在X-Y平面移動了一定的角度損耗了信號的功率,所以并沒有同時實現信號的相位敏感放大,即犧牲了放大的能力來換取更精確的相位量化結果。
技術實現要素:
本發明提供一種在全光信號處理中,信號高精度相位量化的方法,旨在解決現有光相位量化研究結果中存在的量化結果精確度不高、高次諧波與信號的功率比不易精確控制的問題。新的方法帶來更為精確的量化結果、更為方便的功率比控制,同時可以應用到相位調制信號的再生。
本發明提供一種基于相位敏感放大(phase sensitive amplifier,PSA)的多光波干涉相位量化方法,其主要思想是在現有選擇一個特定相位諧波與信號光進行干涉的基礎上,通過引入一個或多個更高次特定諧波對低次諧波的量化結果進行改善和矯正;同時通過干涉光波產生和疊加分開的實現方式來精確控制干涉光波間的功率比,以實現高量化精度的目標。下面從相位敏感放大原理、相位量化結果主要影響因素、多光波干涉相位量化原理幾個部分介紹。
1)相位敏感放大原理:
光域中單色波可以表達為公式(1)所示的形式:
兩個光波間發生干涉前提是頻率相同,因此將雙光波干涉簡化表達為復振幅(即光波幅度和相位)相加的形式,如公式(2)所示,其中,N是量化的階次
將公式(2)進行擴展,可以得到多光波干涉的公式(3),其中, 為相位,在0-2π間變化。
實現相位量化,基礎是滿足相位敏感放大的條件。相位敏感放大在實 現上可以分為兩步:諧波產生和相干疊加。諧波產生是在非線性介質(如高非線性光纖、SOA、PPLN、硅波導等)中,利用非線性效應(如三波混頻、四波混頻等)產生與輸入信號相位匹配的高次諧波;相干疊加是根據量化階次的需要選擇特定諧波,利用非線性效應將滿足相位匹配條件的兩個波轉換成相同頻率并發生干涉,實現相位量化。
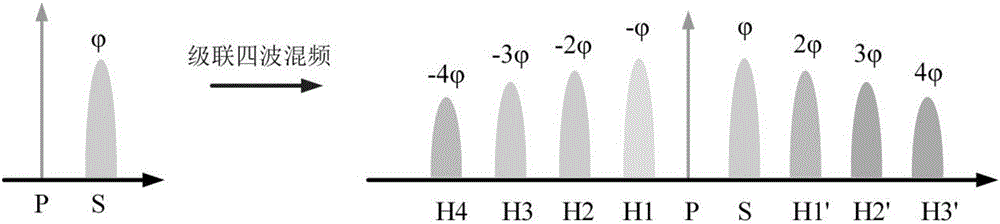
傳統的雙光波干涉相位量化,參與量化的光波分別為信號光和與信號光有固定相位關系的諧波,如果需要量化N階信號,就需要N-1階的諧波與待量化信號干涉。以在光纖中實現相位敏感放大為例,第一步需要在高非線性光纖輸入端同時輸入強泵浦和待量化信號,在光纖中會產生級聯的四波混頻效應。如圖3-2所示,按照四波混頻過程的頻率關系,第一級四波混頻為單泵浦簡并四波混頻過程,產生諧波H1’和H1,頻率關系分別為ωH1'=2ωs-ωP,ωH1=2ωP-ωS,若假定泵浦P相位為0,信號S相位為則第二級四波混頻過程需要有第一級過程產生的新頻率光波作為輸入信號,分為兩種情況,均會產生諧波H2’和H2,一種是簡并四波混頻過程,頻率關系為ωH2'=2ωH1'-ωs,ωH2=2ωH1-ωP,仍假定泵浦P相位為0,信號S相位為則 另一種是非簡并四波混頻,頻率關系ωH2'=ωH1'+ωs-ωP,ωH2=ωH1+ωP-ωS,相位為同理,在泵浦和信號功率足夠強,且高非光纖非線性系數較高時可以發生多級的四波混頻過程,產生高次諧波,且越高級的四波混頻過程越不易發生,故高次諧波的功率在逐漸降低。通過級聯四波混頻過程,會在泵浦光的兩側以泵浦和信號的頻率差為間隔等間隔的產生各級高次諧波,這些高次諧波的相位按照倍數遞增。
若通過級聯的四波混頻過程無法產生需要階次的諧波,則可以通過若干低次諧波間的四波混頻產生該高次諧波。
第二步需要在獲得高次諧波之后,依據量化階次選擇特定諧波進行相干疊加。以信號進行三階量化為例,由Radan Slavl′k等人的研究結果知,需要相位為的信號與待量化信號相干疊加,如圖2所示,首先選擇第一步通過級聯四波混頻生成的相位為諧波H1',通過雙泵浦非簡并四波混頻過程,在信號S的相同頻率處,產生新的諧波S',頻率關系為ωP1+ωP2=ωS'+ωH1',假定泵浦2的相位也為0,則由于新生成的諧波S'與信號波S相同頻率且相位匹配,會在該頻率處發生相干 疊加,將振幅歸一化并用光矢量疊加表示為其中p干涉的量信號功率比,傳統的雙光波干涉一般選擇
2)相位量化結果主要影響因素:
信號的相位量化特性主要受兩方面影響:一是參與干涉的信號的相位關系,二是參與干涉的信號的功率比。相位關系決定量化階次,如圖3(a)星座圖所示,實線為輸入待量化信號,用表示,相位在0-2π間變化,虛線為信號三階量化后結果,用表示,最終的干涉過程表達為 其中為-2次諧波,a的取值為0.5。圖3(b)是相位轉移曲線,信號量化前相位曲線是45度斜向右上的直線;量化后的信號出現了階梯狀的趨勢,但與理想階梯狀量化曲線相比,在與目標相位正交的相位(π/3、π、-π/3)附近,未能實現有效的量化,在相位轉移曲線中表現為“臺階”的邊緣不夠銳化,量化結果還有待提高。
參與干涉信號的功率比影響量化精度。兩信號干涉(即兩個光矢量進行疊加)的結果,受功率比影響可以見圖4,干涉過程表達為: 其中圖4(a)為待量化的信號星座圖,相位在0-2π間變化,幅度為一定值;圖4(b)-4(e)為兩信號干涉后結果,其中功率比a分別為:0.25,0.5,0.75,1。星座圖中曲線圍成的陰影面積,可以表征量化精度的高低,理想的量化陰影面積應該為0。可以看到,隨著功率比的不斷增大,量化結果出現了兩個變化:一是橫線填充的陰影面積逐漸縮小,并且在a=1時為0,即參與疊加的兩光矢量幅度相同,在方向相反的時刻矢量和為0。二是方格填充的陰影部分在a從0變化至0.5時均未出現,超過0.5時在三個量化目標相位(0、2π/3、-2π/3)處同時出現,且在a從0.5變化至1的過程中面積始終增大,并在a=1時達到最大值,方格填充的陰影部分的出現代表相位“過量化”現象。可以發現,隨著a的增大,橫線填充的陰影部分面積與方格填充的陰影部分面積的變化趨勢相反,兩者不可能同時達到最小值。即,無論如何調節功率比a,只能得到該條件下的相對最優解,而無法實現理想的相位量化。
3)多光波干涉相位量化原理:
將信號量化為N階,通常采用-(N-1)次諧波與其干涉,除此之外,(N+1)次相位諧波也可實現信號的N階量化。如圖5(a)所示,原始信號相位在0-2π間變化,與4次相位諧波矢量疊加后星座圖如5(b)所示,數學表 達式為其中a=0.2。可以看到,4次相位諧波與信號發生干涉,對π/3、π、-π/3附近的相位產生向內的壓縮作用,對-2π/3、0、2π/3附近的相位產生向外的拉伸作用,這在一定程度上同樣實了信號的三階量化。圖5(c)所示為信號與-5次相位諧波干涉,數學表達式為 其中a=0.2,量化后的信號出現6個峰值。
總的來說,-(N-1)次相位諧波與信號干涉后的結果是將目標相位附近的相位向外拉伸,將與目標相位正交的相位向里壓縮;(N+1)次相位諧波與信號干涉后的結果是將目標相位附近的相位向內壓縮,將與目標相位正交的相位向外擴展。利用不同階次相位諧波與信號干涉后的不同結果,選擇多個合適諧波的與信號作用,能夠實現更為精確的量化結果。
以信號三階量化為例。可以發現,能夠將信號量化為三階的兩個諧波:-2次諧波和4次諧波,對信號的量化作用恰好是互補的。將4次諧波作為-2次諧波和信號干涉結果的修正,可解決相位“過量化”現象且進一步將目標相位的正交相位向內壓縮。三光波干涉三階量化的數學表達式為 其中a,b<0,若要實現好的量化結果,需要合理選擇三者之間的功率比,即a、b的取值。如圖6所示,圖6(a)、6(b)、6(c)分別為待量化信號、-2次諧波與信號以功率比0.7干涉、4次諧波與信號以功率比0.2干涉。圖6(d)、6(e)、6(f)為三光波量化結果,a、b取值分別為0.7,0.08;0.7,0.12;0.7,0.18。對比6(b)、6(d)、6(e)、6(f)四圖可發現,隨著b的取值不斷增大,橫線填充的陰影部分的面積在逐漸縮小,即目標相位的正交部分得到了進一步壓縮。對于過量化的部分,當b的取值較小時,不能夠進行完全矯正,如圖6(d)所示;當b的取值較大時,會出現過矯正現象,使其遠離目標相位,如圖6(f)所示;當b取合適值時,矯正效果最好,目標相位附近幾乎量化為一條直線。
將三波干涉相位量化推廣到四波乃至更多相位諧波的干涉,使高次諧波作為低次諧波量化結果的微調,合理控制干涉光波間的功率比,可以實現近乎理想的相位量化。如圖7(a)所示,四個光波進行干涉,數學表達式為:其中a=0.8,b=0.29,c=0.125。從星座圖中可以看出相位在0-2π間變化的信號量化后幾乎全部被壓縮到三個目標相位處,實現了近乎理想的相位量化。圖7(b)為待量化信號、雙光波干涉、三光波干涉、四光波干涉以及理想量化的相位轉移曲線。隨著 參與量化的諧波數目的增加,同時合理調節各諧波的功率,相位轉移曲線越來越接近理想量化曲線。星座圖中圓心處壓縮的越好,相位轉移曲線在各量化階次間的躍變越接近階躍函數;星座圖中目標相位徑向上越接近一條直線,相位轉移曲線在同一個量化等級內的變化越小,接近一條水平直線。
附圖說明
圖1級聯四波混頻產生諧波示意圖
圖2四波混頻光波干涉示意圖
圖3雙光波三階相位量化星座圖及相位轉移曲線
圖4雙光波三階相位量化不同功率比星座圖及相位轉移曲線
圖5不同階次相位諧波干涉結果
圖6多光波干涉不同信號功率比結果
圖7四光波干涉星座圖及相位轉移曲線
圖8三光波干涉相位三階量化結構示意圖
圖9三光波干涉相位三階量化結果星座圖
圖10三光波干涉相位三階量化結果相位分布直方圖
具體實施方式
為了使本發明的目的、技術方案及優點更加清楚明白,以下結合附圖及實施例,對本發明進行進一步詳細說明。應當理解,此處所描述的具體實施例僅用以解釋本發明,并不用于限定本發明。
實施例:
本實施例基于如圖8所示的三光波干涉相位三階量化仿真結構示意圖對多光波干涉高精度相位量化進行說明。
第一部分為高次諧波產生。信號和泵浦光1一同輸入高非光纖1中,其中泵浦光的頻率為193.1THz,功率為100mw。信號光的產生由圖8左下信號產生部分示出,信號光源和正弦波共同輸入到相位調制器中,相位調制器的傳輸函數為:其中Ein(t)為輸入的光信號,頻率為193.13THz,功率為1mw;data(t)為輸入電域正弦波,幅值為1,頻率為50M;為相位調制器內部的相位偏移,設置為180°。相位調制器輸出相位在0-2π間變化的信號。高非光纖1的非線性系數為13w-1/km,長度為1km。高非光纖1的輸出為等間隔分布的級聯四波混頻產 生的高次諧波,間隔為泵浦1與信號的頻率差:30GHz。
第二部分為信號同頻相位諧波產生。頻率選擇開關從級聯四波混頻生成的各次諧波中選出需要的兩個諧波和并分別送入上路和下路,上下兩路結構相同,只是參與反應的諧波和泵浦的頻率、相位不同。為保證實現相位量化,每一路參與作用的兩個泵浦必須是相位相干的,即兩者需要有固定的相位差。通過相位調制器可生成光梳,這些不同頻率的光波之間滿足相干關系。上路選擇相位為頻率為193.16THz的諧波H1',由光梳生成的泵浦1、2的頻率分別為193.1THz和193.19THz。三個光波一同輸入到高非光纖2(非線性系數為13w-1/km,長度為500m),發生雙泵浦非簡并四波混頻,根據四波混頻發生的頻率關系ωP1+ωP2=ωH1'+ωS1在與信號相同頻率處產生相位為的光波S1,再通過中心頻率為193.13THz的帶通濾波器濾出S1。下路選擇相位為頻率為192.98THz的諧波H4,由光梳生成的泵浦1、3的頻率分別為193.1THz和193.01THz。三個光波一同輸入到高非光纖3(非線性系數為13w-1/km,長度為500m),發生雙泵浦非簡并四波混頻,根據四波混頻發生的頻率關系ωP1+ωP3=ωH4+ωS2在與信號相同頻率處產生相位為的光波S2,再通過中心頻率為193.13THz的帶通濾波器濾出S2。
第三部分為同頻率信號干涉。相位為的原始信號經過延時器后,與濾波器輸出的光波S1、S2在光耦合器中相遇并發生干涉,由于信號光S與S1、S2經過的路徑與器件不同,在相位匹配上會有一定的偏差,延時器可以起到微調信號相位的目的,實現精確的相位匹配。通過上述三個步驟后輸出的信號即為三階相位量化后的信號。
多光波干涉相位量化的仿真結果如圖9所示,圖9(a)為輸入的待量化原始信號星座圖,相位在0-2π間變化;通過兩次四波混頻過程,最終在與信號相同頻率處產生的相位為的光波與信號單獨發生干涉后的量化結果星座圖如圖9(b)所示,兩者的功率比為0.72:1(的諧波:信號);同樣通過兩次四波混頻過程,在與信號相同頻率處產生的相位為的光波與信號單獨發生干涉后的量化結果星座圖如圖9(c)所示,兩者的功率比為0.12:1(的光波:信號);上述三個光波按照功率比1:0.72:0.12一同發生干涉,量化結果星座圖如圖9(e)所示,與傳統雙光波干涉實現的相位量化結果(圖9(d)所示)相比,信號得到了更好的壓縮,尤其體 現在與量化目標相位正交(90°、210°和330°)的相位部分,幾乎全部被壓縮到的三個目標相位處,星座圖中已經可以明顯看到三條直線。從相位轉移曲線(圖9(f)所示)中可以看出,其中橫坐標為輸入信號相位,縱坐標量化后的輸出信號相位,傳統雙光波干涉結果雖然一定程度上實現了階梯狀輸出,但是在每個“臺階”上,并不是十分平坦,而三光波干涉結果每個臺階幾乎與X軸平行,即對于在一定范圍內變化的輸入信號相位,全部量化至同一相位;觀察每個臺階的轉換處(可稱作過度相位),傳統雙光波干涉曲線的斜率小于三光波干涉結果,且有更多的相位點處在過度位置,而處在過度位置的三波量化后的點點則大大減少,基本變成了一個階躍函數,即有更多的相位被量化至目標相位,量化結果更加精確。
傳統雙光波干涉量化結果與三光波干涉量化結果的相位分布直方圖如圖10所示。圖中,橫坐標為信號量化后的相位,縱坐標為某特定相位對應的相位點數。其中,圖10(a)為雙光波干涉量化結果,可以看到,相位有在三個區間(15度、135度和255度)聚集的趨勢,但是幾乎在(-π,π)的所有范圍內都有相位的分布,并不能集中在被量化到的三個區間,圖中縱坐標的最大值也小于20,即信號沒有得到有效的量化。圖10(b)為三光波干涉三階相位量化的相位分布直方圖,可以看到,相位在三個區間(15度、135度和255度)有較傳統雙光波干涉更為集中的分布,同時更突出的是,信號在其他相位的分布數大大減少,已經可以較為明顯的看到三個不相連的相位聚集區域,圖中縱坐標的最大值已經較圖10(a)有增加,變為22,也證明對于信號的量化更加精確。經計算,傳統雙光波干涉量化結果的相位分布方差為3.3821,本論文提出的三光波干涉量化結果的相位分布方差為2.4434,降低了了27.8個百分點。從另一個角度論證了多光波干涉相位量化較傳統量化方式具有精度更高的優點。
- 還沒有人留言評論。精彩留言會獲得點贊!