本發明涉及檢測技術與信號處理領域，具體涉及一種焊接電流實時測量計算方法，可應用于單相交流電阻點焊機電流測量計算及類似電路的環境。

背景技術：

在單相交流電阻點焊機設備中，流經金屬焊片的電流值是一個重要的控制參數和過程變量。目前大部分的電阻焊機都是以電流值作為控制變量輸入的，也即根據電流值在調整焊接電源的輸入。同時，電流值還可以作為重要的計算參數，用以在線質量估計模型的建立。另外，電流值還可以用以動態電阻值的計算，以用于焊接過程分析以及控制策略設計，焊接安全性操作的在線檢測等。這些應用大部分需要用到實時數據計算，而當前的電阻點焊電流值測量，通常使用均方根值來對每一個采集值進行計算，需要采集的實時數據量很多，計算涉及到的數學算法步驟復雜，計算量大，對于以微處理器系統為主的中央處理系統造成很大的壓力。

在單相交流電阻焊機中，唯一的輸入參數為每一個控制周期的晶閘管觸發角α，主要決定了有多少能量進入焊接系統，當能量進入后即在每一個控制周期內產生了持續一定時間的焊接電流，在傳統的方法中，是根據平方和開方-也即離散點逐次積分的方法求得，具體是對在數據采集的每一個點，均需要做平方運算，然后相加，最后除以總數N(一個周期內采集到的電流值的個數)以及開平方，工作量很大。通常在以微處理器為主要工具的點焊操作中，計算空間非常有限，因此這樣的運算給其他運算以及整體任務的完成造成很大壓力，必須用更加有效快速的方法予以改進。

方云等人通過理論分析，建立了不同功率因數角的電流有效值系數神經網絡計算模型，進而推算出在1/2周期內估計出電流有效值的計算方法，但是這種方法與具體建立模型的焊接過程有關，使用范圍非常有限，而且計算過程也較為復雜。貢亮等人建立了電流過零微分值與電流有效值之間的數學關系，進而同樣利用神經網絡建立了數學模型，但是神經網絡過程過于復雜，且分析過程同樣與單一實驗環境有很大的關系，導致誤差較大，也只能利用在比較簡單的應用中。

由于電阻點焊的應用越來越廣泛，實時計算越來越復雜，對微處理器的計算速度要求也越來越高，亟需發明一種計算更為簡單、計算方面更為通用的電流測量方法。

技術實現要素：

本發明的目的在于克服現有技術的缺點和不足，根據電阻點焊機的電力系統特性，從電流有效值計算的基本原理和方法出發，提供通用性強，計算工作量小的一種焊接電流實時測量計算方法。

本發明的目的通過下述技術方案實現：

(1)以晶閘管觸發角α為單相交流電阻點焊機唯一輸入參數，控制輸入焊接系統能量；

(2)通過模擬-數字采集裝置采集焊接電流i_d；

(3)通過采集到的焊接電流i_d，搜索電流序列最大值所在的采集時間點γ；

(4)計算一個周期內電流的導通角θ；

(5)根據觸發角α，導通角θ與功率因數角之間的數學關系求解功率因數角；

(6)計算依賴模型部分有效值I_RMS1；

(7)利用神經網絡方法計算不依賴模型部分有效值I_RMS2；

(8)計算最終的焊接電流有效值I_RMS。

進一步，步驟(4)中的導通角θ按以下公式計算：

式中N為一個控制周期內電流采集值的總個數，f_s為電流數據采樣頻率，Tc為控制周期，在工頻為50Hz的情況下，一般為10毫秒。

進一步，步驟(5)中的功率因數角按以下公式計算：

式中T_s為電流數據采樣周期，M為到達每一個控制周期內電流峰值時的電流采集值的個數，γ為電流峰值，f為工頻頻率，即50Hz，ω為角頻率。

進一步，步驟(6)中的依賴模型部分有效值I_RMS1按以下公式計算：

式中，U為電壓和Z為系統等效阻抗。

進一步，步驟(7)中的不依賴模型部分有效值I_RMS2計算采用神經網絡方法計算可以大大節省運算時間，神經網絡架構使用2×5×1形式可以取得較好效果。以P＝[α，θ]^T為輸入值，離線訓練獲得神經網絡輸入層與隱層之間的權值W_I，隱層與輸出層之間的權值W_II；輸入層與隱層之間的偏離值B_I和隱層與輸出層之間偏離值B_II，控制系統實時計算過程如下：

T₁＝W_I·P+B_I (4)

I_RMS2＝W_II×T₂+B_II (6)

式中T₁，T₂均為5行1列的矩陣，T_1，i，T_2，i表示矩陣中每一個具體的元素。

進一步，步驟(8)中的最終的焊接電流有效值I_RMS按以下公式計算：

1_RMS＝I_RMS1×I_RMS2 (7)

本發明與現有技術相比，具有如下優點和有益效果：

本發明主要根據單相交流電阻點焊機電路系統的基本原理，結合數學積分運算，推理出每一個焊接控制周期有效值計算的公式，將有效值計算分解為依賴模型部分和不依賴與模型部分，對于依賴模型部分采用峰值直接除法的方式，而對于不依賴模型部分采用神經網絡建模。更為重要的是，不依賴模型部分對于所有的單相交流電阻點焊操作而言都是一樣的，完全可以事先確定好，在具體需要計算的時候再代入計算，增強了本方法的普遍適用性。這樣可以實現從原理上直接求解電流有效值，而且計算過程簡單，計算量小，可以大大改進當前的依賴于均方根計算逐次積分有效值的方法。

附圖說明

圖1.本發明一種焊接電流實時測量計算方法流程圖；

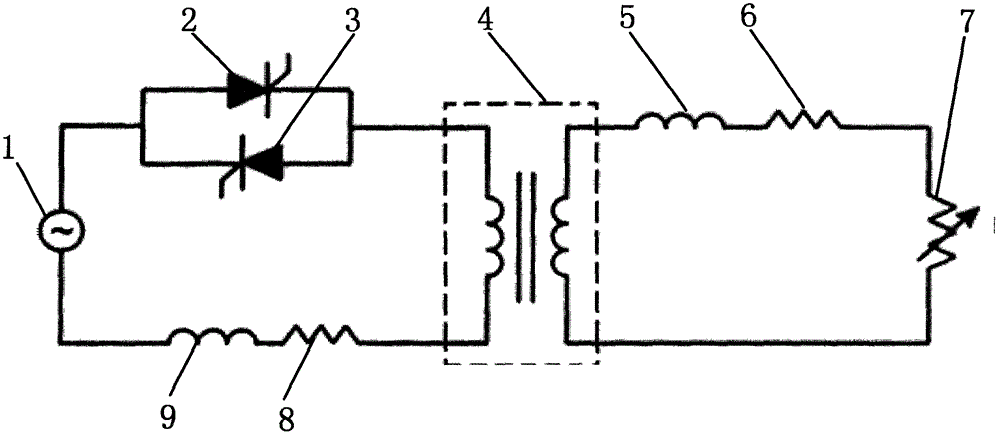
圖2.單相交流電阻點焊機電路系統原理圖；

圖3.本發明實施例觸發角為104.4°時，兩種方法電流有效值曲線對比圖；

圖4.本發明實施例觸發角為104.4°時，電流計算誤差曲線圖；

圖5.本發明實施例觸發角為109.8°時，兩種方法電流有效值曲線對比圖；

圖6.本發明實施例觸發角為109.8°時，電流計算誤差曲線圖；

圖7.本發明實施例觸發角為113.4°時，兩種方法電流有效值曲線對比圖；

圖8.本發明實施例觸發角為113.4°時，電流計算誤差曲線圖；

圖9.本發明實施例觸發角為117°時，兩種方法電流有效值曲線對比圖；

圖10.本發明實施例觸發角為117°時，電流計算誤差曲線圖；

圖11.本發明實施例觸發角為120.6°時，兩種方法電流有效值曲線對比圖；

圖12.本發明實施例觸發角為120.6°時，電流計算誤差曲線圖。

附圖說明：1-焊接電源；2-晶閘管1；3-晶閘管2；4-焊接變壓器；5-次級線圈的等效電感；6-次級線圈的等效電阻；7-負載；8-主線圈的等效電感；9-主線圈的等效電阻。

具體實施方式

下面將結合本發明實施例中的附圖，對本發明實施例中的技術方案進行清楚、完整地描述，顯然，所描述的實施例僅僅是本發明一部分實施例，而不是全部的實施例。基于本發明中的實施例，本領域普通技術人員在沒有做出創造性勞動前提下所獲得的所有其他實施例，都屬于本發明保護的范圍。

請參閱說明書圖1：

圖1為本發明一種焊接電流實時測量計算方法的流程圖，具體包括如下步驟：

(1)以晶閘管觸發角α為單相交流電阻點焊機唯一輸入參數，控制輸入焊接系統能量；

(2)通過模擬-數字采集裝置采集焊接電流i_d；

(3)通過采集到的焊接電流i_d，搜索電流序列最大值所在的采集時間點γ；

(4)計算一個周期內電流的導通角θ；

(5)根據觸發角α，導通角θ與功率因數角之間的數學關系求解功率因數角；

(6)計算依賴模型部分有效值I_RMS1；

(7)利用神經網絡方法計算不依賴模型部分有效值IRMS2；

(8)計算最終的焊接電流有效值I_RMS。

請參閱說明書圖2：

在圖2單相交流電阻點焊機電路系統原理圖中，焊接電源1通過晶閘管2、3的觸發角α為系統輸入參數，控制輸入能量；焊接變壓器4實現降壓，之后提供能量給負載7，焊接電流i_d為流經負載7的電流數字采集值。5為次級線圈電路的等效電感；6為次級線圈電路的等效電阻；8為主線圈電路的等效電感；9為主線圈電路的等效電阻。

本發明以普通單相交流電阻點焊操作為例，實驗平臺包括電阻點焊機，電流測量儀器羅氏線圈，工控機，控制及數據采集電路板等，其中控制及數據采集電路板為自行研制而成，微處理器采用DSP進行設計，以常規的連續逐次積分方法為基準進行計算。電壓為380V的標準電壓，焊接有效控制時間均為20個控制周期(每個控制周期為10毫秒)。

選擇晶閘管觸發角度分別為104.4°，109.8°，113.4°，117°和120.6°這5種情況，分別采用本發明一種焊接電流實時測量計算方法與常規的連續積分方法進行計算，并對計算結果進行對比。每個觸發角度時兩種方法電流有效值對比曲線圖和電流計算誤差曲線圖見說明書圖3至圖12。可以看出兩種方法計算誤差很小，基本在-200A至400A之間振動，平均誤差不超過1.6％，最大誤差不超過3.5％。

表1為不同觸發角情況下兩種方法誤差與CPU處理時間的對比。

表1.不同觸發角情況下兩種方法誤差與CPU處理時間對比

結果可以看出，誤差很小，但是本發明CPU工作完成時間遠遠低于傳統方法CPU工作時間，且傳統處理方法在前三組觸發角情況下，根本無法完成在線計算。

本實施例所述一種焊接電流實時測量計算方法應用過程如下：晶閘管觸發角是單相交流電阻點焊機的唯一一個輸入，每一個控制周期需要一個晶閘管觸發角來決定有多少能量進入焊接系統中，進而熔化固態金屬。當能量進入焊接系統后，產生電流，通過羅氏線圈，根據合適的采集頻率(本實施例中使用的采集頻率為6.4kHz)采集電流數值，即為i_d，當采集完成后，可以相應的得到電流峰值γ，計算功率因數角以及電流作用域范圍導通角θ。根據這幾個數值可以計算依賴模型部分有效值I_RMS1，構建計算非模型依賴部分的神經網絡系統，之后計算不依賴模型部分有效值I_RMS2。由于神經網絡模型是基于不依賴模型部分，因此可以適用于任何相似電路中，也即構建一次之后，以后可以無限次的使用。分別計算出電流有效值的兩個部分I_RMS1和I_RMS2后，最終計算總的電流有效值I_RMS。

盡管已經示出和描述了本發明的實施例，對于本領域的普通技術人員而言，可以理解在不脫離本發明的原理和精神的情況下可以對這些實施例進行多種變化、修改、替換和變型，本發明的范圍由所附權利要求及其等同物限定。