本發明屬于現代振動篩分裝置，涉及一種三機驅動雙質體亞共振自同步概率等厚篩。

背景技術：

在現代篩選機械技術領域內，振動篩是工礦企業普遍應用的篩分機械，用作物料的篩分、分級、洗滌、脫介、脫水之用。篩分技術的水平的高低和質量的優劣，關系到工藝效果的好壞生產效率的高低和能源的節省的程度，從而直接影響企業的經濟效益。一般振動篩篩分效率低、篩分時間長，振動篩機構過于傳統，不能實現設備的大型化，作為現在篩分機械的新理念，振動篩要求要與原有篩分機械在結構上有所創新，打破機體的整體化，和結構的統一化，其次，傳統篩分效率低、物料篩分不徹底、能耗大、結構笨重，這些從較大的方面限制了傳統篩的使用壽命。本發明在解決傳統振動篩的缺點之余，應用三機自同步理論、亞共振的機構、概率等厚篩分方法的應用，使得振動篩的效率成倍的提高。

本發明屬于振動篩分設備中一種新型結構和新技術的整體有機結合，原理和傳統振動篩分機相，同采用的電動機驅動篩分物料，傳統篩分機往往產生許多問題：

1.傳統振動篩一般采用單機驅動或雙機同步驅動所需的電動機功率大，進而能耗增加，電動機本身體積也大，對電動機的技術要求也提高。

2.傳統振動篩通常采用單質體，在實現設備大型化有很大的難度，傳給基礎的動載荷較大，對振動篩本身的強度要求特別高。

3.傳統振動篩一般采用齒輪傳動強迫聯系的激振器，雖然結構緊湊成本低，但是由于振動篩振動次數較高，振幅較大，對齒輪的加工精度和潤滑要求特別高。隨著對振動篩的要求不斷的提高，使得振動篩的機構、性能各方面都有進一步的創新。

技術實現要素：

針對目前傳統振動篩，由于篩分效率低，篩分物料分離不徹底，和結構上過于陳舊，核心理論方法上不創新。本發明在傳統的結構上打破了傳統結構保守的結構模式，并應用新的同步理論和現代篩分技術來實現新的革新，結合三機自同步理論、亞共振機構、概率等厚篩分方法的應用，使得振動篩的效率成倍提高。

本發明是通過以下技術方案來實現的：

一種三機驅動雙質體亞共振自同步概率等厚篩，包括偏心轉子、交流電動機、撓性聯軸器、主振彈簧、導向板、篩箱、三成篩板、減振彈簧、基座、支撐架，分為上質體和下質體：上質體有交流電動機驅動偏心轉子組成激振器構成上質體，篩箱構成下質體；在基座上分別有四組減震彈簧組與箱體通過彈簧組相連接前后左右對稱分布在篩箱兩側，篩箱中部兩側均有一伸出結構作為支撐面，與主振彈簧和導向板互成夾角與上質體連接，上質體有三個偏心轉子和三個交流電動機通過撓性聯軸器共同組成三個激振器組成篩箱，前部為進料端，后部為出料端，與進料端鄰接處裝有三層篩分的篩板，用于概率快速分層物料，電動機支撐架支撐三個驅動電動機，位于篩箱的一側。它采用雙質體亞共振設計理論，運動方式為兩個質體相對運動；具有亞共振系統設備的激振頻率小于振動系統的固有頻率；當振動電動機所帶動的偏心轉子在上質體工作時，所產生的激振力使得上質體振動，激振力通過主振彈簧使得下質體振(箱體)振動；由偏向轉子產生的激振力驅動上質體，上質體的振幅通過主振彈簧加以放大，從而產生下質體所要求的有效振幅，物料從進料端進入，均勻分散在篩板之上快速實現概率分層以防物料堆積，并通過振動而輸送至單層篩網段并實現等厚高效篩分；下質體所產生的振動被減振彈簧有效隔離，從而保證大振動不能傳播到地基，避免造成對周邊環境的影響。

進一步地，主振彈簧與導向板彈簧夾角為90°，且主振彈簧與物料前進方向成45°，也即振動方向角為45°。

上述三機驅動雙質體亞共振自同步概率等厚篩的參數確定方法，包括如下步驟：

步驟1，建立動力學模型和運動微分方程

振動系統的動力學模型，其中主振動體由兩個剛體和三對偏心轉子組成；剛體a通過彈簧和導向板分別連接到基座和剛體b上，而三個偏心轉子安裝在剛體b上；另外，振動彈簧與x軸平行且和導向板垂直；三個偏心轉子分別繞偏心轉子旋轉軸中心o1，o2和o3旋轉，并且旋轉中心o1,o2,o3共線；感應電動機驅動三個偏心轉子以逆時針方向旋轉；分別是三個偏心轉子的旋轉角；由于導向板的限制作用，可以假定整個系統只有沿x方向的一個自由度，用x表示；

基于拉格朗日方程，振動系統的運動微分方程得出如下。

m1＝m1；m2＝m2+m01+m02+m03；m＝m1+m2joi＝m0iri²；r1＝r2＝r；m01＝m02＝m01、兩個剛體在x方向的相對運動微分方程

假設三個偏心轉子的質量:m01＝η1m0；m02＝η2m0；m03＝η3m0(和η1＝1)三個偏心轉子的平均相位為其相位差為2α1，2α2，2α2，且它們的關系如下

當三個偏心轉子同步運行時，它們的同步角速度為然后，在穩態下其位移和角加速度的關系可以如下表示

偏心轉子的角加速度在穩定狀態下接近于零，即將公式(3)插入到(1)的前兩個公式中，且其中f1x可以被忽略(相對于其他參數，f1x非常小)。

在式(4)和(5)，k1x<<k2x，m'2＝m2。

在穩態下，有變換公式(4)和(5)：然后代入公式(2)，得出兩個剛體m1和m2在x方向上的相對運動微分方程。

m是振動系統的誘導質量。

根據公式(6)可以得到兩個剛體的相對運動固有頻率ω0(也稱為主振動系統的固有頻率)。

方程(6)的響應如下

對于具有小阻尼的振動機，在工程上有f2x＝2ξ2xmω0。其中ξ2x是等效的相對阻尼系數，且ξ2x≤0.07。

根據式(8)，當z0＝1(即ωm0＝ω0)，a21的值達到最大。這表明ω0是x方向上兩個剛體之間的反相位運動的固有頻率。

基于求解極值規則，具有反相位相對運動的響應幅值λ21可以表示如下。

λ21的值在工程中非常重要，其將在后面部分中詳細討論。

步驟2，推導同步性條件

考慮式(2)，通過傳遞函數方法求解(1)的前兩個公式，得系統穩態下的響應：

(1)三個偏心轉子的同步判據

從式(1)的前兩個公式中，可以得到x方向上的兩個剛體的耦合矩陣和特征方程。

其中m'是慣性耦合矩陣，k'是剛度耦合矩陣，δ(ω²)是特征值的特征方程。當δ(ω²)＝0時，有

ω⁴m1m2-ω²m1k2-ω²m2k2-ω²m2k1+k1k2＝0(12)

基于式(12)，可以求解兩個剛體在x方向上的兩個固有頻率：

在工程中，隔振系統的剛度k1x遠小于主振動系統的剛度k2x(即k1x<<k2x)。因此，忽略ω′inv中的k1x(即k1x＝0)，我們有ω′inv≈ω0。這表明，ω′inv是兩個剛體在x方向上的反相位相對運動的固有頻率。顯然，ω′sa則是兩個剛體在x方向上同相位相對運動的固有頻率。

當三個偏心轉子同步運行時，它們的同步角速度對式(10)二次微分，然后將結果分別代入式(1)后面的三個公式中，并將它們在上積分。在重排之后，可以獲得三個偏心轉子的平衡微分方程。

其中為電動機i的輸出電磁轉矩。是標準偏心轉子對的動能

在上述積分過程期間，與隨時間t的的變化相比，2α1和2α2的變化小得多，其可以被看作為是慢變參數.因此，故2α1和2α2可以用它們的積分均值和代替。

電動機a和b之間以及電動機b和c之間的輸出電磁轉矩之差如下：

重新整理公式(15)

其中，τc12(α1，α2)，τc23(α1，α2)分別是電動機a和b，b和c的無量綱耦合力矩。其約束函數如下：

因此得到三個偏心轉子的同步判據如下

方程(22)和(23)可以描述為：任意兩個激振器之間的無量綱殘余力矩之差的絕對值小于或等于其無量綱耦合力矩的最大值。

將式(14)中公式相加并重新排列，得到三個電動機的平均無量綱負載力矩。

其約束函數如下

定義ζi,j(i,j＝1，2，3)為偏心轉子a和b，b和c，a和c之間的同步能力的系數，其表達式如下。

同步能力的系數ζ12，ζ23和ζ31越大，振動系統的同步能力越強，振動系統更容易實現同步。

步驟3推導穩定性條件

振動系統的動能(t)和勢能(v)如下

單個周期內振動系統的平均動能和勢能可求得：

振動系統單周期上的hamilton平均作用量：

在同步狀態下，系統的穩定相位差解對應于hamilton的平均作用量的最小值。即i的hesse矩陣應該在穩定同步解的鄰域內正定。

如果i的hesse矩陣是正定的，則有

a>0，ac-b²>0(33)

(1)考慮系統阻尼的情況

將式(32)代入式(33)中，并重新排列，可以獲得同步狀態的穩定性判據。

其中h可以稱為振動系統的同步穩定性系數。

(2)忽略系統阻尼的情況

通常，振動機的系統阻尼小，因此可以忽略。在忽略系統阻尼之后，式(34)可以表示如下。

(3)在一些工程機械振動中

在工程中，如振動輸送機，考慮到機械結構和工程設計要求，三臺電動機的參數相同，工作時其相位差接近零。此外，通常在設計過程中得到一系列系統的固有頻率，且有0<ω′sa<ω1<ω′inv。因此，等式(36)可以大致簡化如下。

方程(35)和方程(37)可以被認為是工程設計中穩定性判據的最簡表達式。在這種條件下，當三個偏心轉子工作在亞諧振狀態或亞臨近諧振狀態時，它們的相位差穩定并接近零。

該新型振動篩采用了雙質體亞共振結構、三機自同步理論，提高了設備的運轉效率，降低了設備的高度、減少了維護量，適合于各種大型、超大型工業應用。

本發明的有益效果：

1)雙質體是振動設備的一類新型結構，采用一個質體驅動另一個質體。激發質體通常有電動機驅動的偏心轉子外殼和篩箱的一組彈簧構成，使用彈簧鏈接另一個質體，這樣就形成了一個敏感的亞共振系統，并不因為裝載量的變化而影響整體機械性能的發揮。與單質體系統相比，雙質體系統用較小的功率就可以達到相同的功效，雙質體驅動系統能夠很好的降低電能消耗，在同樣工作的條件下能節約50％～70％的電能。

2)三機驅動，改變傳統驅動理論的思想，采用三機驅動應用了自同步理論。與傳統的單級和雙級驅動相比增大了驅動的頻率，使得篩分更徹底，進一步提升了工作效率。振動系統具有兩個剛體，三個不相同的耦合激振器具有相同的旋轉方向，實現自同步理論。

3)概率等厚篩分技術的應用，與傳統的單層篩分所不同，不僅能夠實現物料的分層，還能有利于物料篩分更徹底，使物料獲得更精確地篩分。概率等厚篩分法綜合了概率篩分法的單位面積產量大以及設備尺寸小的優點，同時克服了概率篩分法效率低和篩下產品中常含有粗顆粒的缺陷以及等候篩分法篩面長度較大的缺點。因此概率等候篩分法已經成為一種較為完善的篩分方法，具有單位面積產量大、篩分效率高、所需篩面長度較小的優點。

4)篩網，采用若干個小塊拼接來代替傳統的整體式篩網，篩面無螺栓連接，可以保證平緩的無障礙的篩分過程，篩網可以根據損壞程度進行局部更換，方便節約成本。

附圖說明

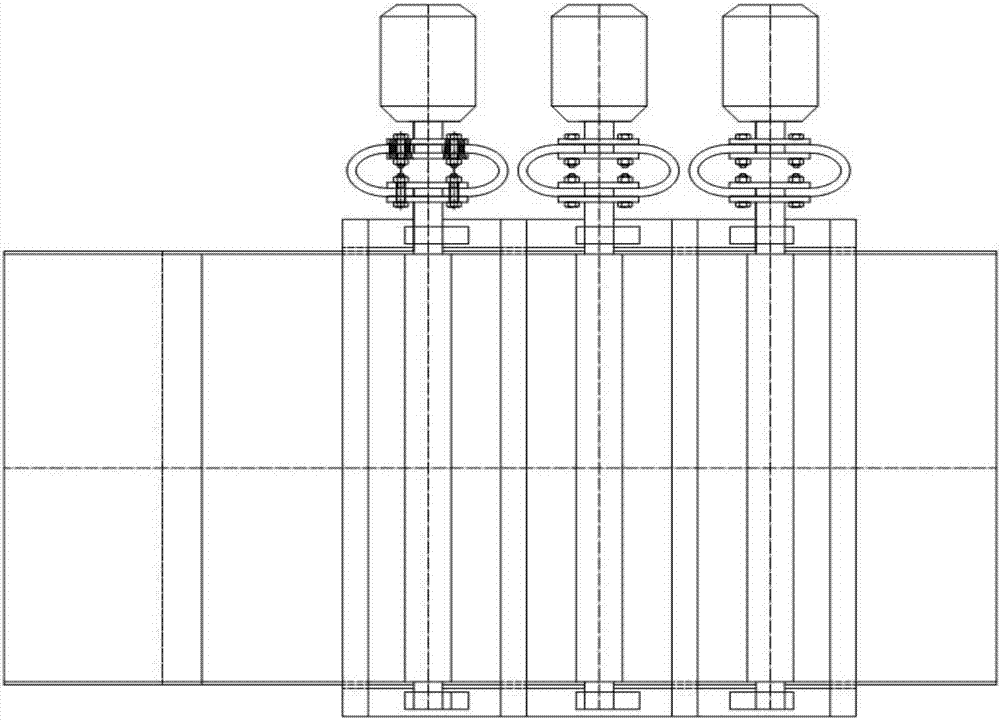
圖1為振動篩結構示意圖主視圖；

圖2為振動篩結構示意圖俯視圖；

圖3為振動篩結構示意圖左視圖；

圖4為振動系統動力學模型圖；

圖5為頻率-振幅曲線圖；

圖6為不同ηi下τcijmax(ij＝1,2,3)隨ωm0的變化圖；

圖7為不同ηi下cgdss隨ω的變化圖：(a)η1＝η2＝η3＝1下曲線；(b)η1＝η2＝1，η3＝0.6下曲線；(c)η1＝1η2＝0.8，η3＝0.6下曲線；

圖8為不同ηi下偏心轉子間的相位差隨ω的變化圖：(a)η1＝η2＝η3＝1；(b)η1＝η2＝1，η3＝0.6；(c)η1＝1，η2＝0.8，η3＝0.6；

圖9為不同ηi下振動系統的同步穩定性系數隨ω的變化圖：(a)η1＝η2＝η3＝1；(b)η1＝η2＝1，η3＝0.6；(c)η1＝1，η2＝0.8，η3＝0.6；

圖10為兩個剛體的相位滯后角隨ω的變化圖；

圖11為η1＝η2＝η3＝1時在亞共振狀態下(z0≈0.24)的仿真結果圖：(a)三個電動機的旋轉速度；(b)偏心轉子a和b之間的相位差、(c)偏心轉子b和c之間的相位差；(d)偏心轉子a和c之間的相位差；(e)剛體a在x方向上的位移；(f)剛體b在x方向上的位移；(g)剛體a和b在x方向上的相對位移；

圖12為η1＝1，η2＝0.8，η3＝0.6時亞諧振狀態下(z0≈0.24)的仿真結果圖：(a)偏心轉子a和b之間的相位差；(b)偏心轉子b和c之間的相位差；(c)偏心轉子a和c之間的相位差；(d)剛體a和b在x方向上的相對位移；

圖13為η1＝η2＝η3＝1時亞共振狀態下(z0≈0.63)的仿真結果圖：(a)三個電動機的轉速；(b)偏心轉子a和b之間的相位差；(c)偏心轉子b和c之間的相位差；(d)偏心轉子a和c之間的相位差；(e)剛體a在x方向上的位移；(f)剛體b在x方向上的位移；(g)剛體a和b在x方向上的相對位移；

圖14為η1＝1，η2＝0.8，η3＝0.6時亞共振狀態下(z0≈0.63)的仿真結果圖：(a)偏心轉子a和b之間的相位差；(b)偏心轉子b和c之間的相位差；(c)偏心轉子a和c之間的相位差；(d)剛體a和b在x方向上的相對位移；

圖15為η1＝η2＝η3＝1時超共振狀態下(z0≈1.26)的仿真結果圖：(a)三個電動機的轉速；(b)偏心轉子a和b之間的相位差；(c)偏心轉子b和c之間的相位差；(d)偏心轉子a和c之間的相位差；(e)剛體a在x方向上的位移；(f)剛體b在x方向上的位移；(g)剛體a和b在x方向上的相對位移；

圖16為η1＝1，η2＝0.8，η3＝0.6時超共振狀態下(z0≈1.26)的仿真結果圖：(a)偏心轉子a和b之間的相位差；(b)偏心轉子b和c之間的相位差；(c)偏心轉子a和c之間的相位差；(d)剛體a和b在x方向上的相對位移；

圖中：1篩板；2進料口；3偏心轉子；4激振器；5主振彈簧；6導向板；9減振彈簧；10支撐面；11隔板；12撓性聯軸器；13電動機。

具體實施方式

如圖4振動系統的動力學模型，其中主振動體由兩個剛體和三個偏心轉子組成。剛體a通過彈簧和導向板分別與基座和剛體b連接，且三個偏心轉子安裝在剛體b上。另外，振動彈簧與x軸平行且和導向板垂直。三個偏心轉子分別繞偏心旋轉軸中心o1，o2和o3旋轉，并且旋轉中心o1，o2，o3共線。感應電動機驅動三個偏心轉子一起逆時針旋轉。在文中，分別是三個偏心轉子的旋轉角。由于導向板的限制作用，可以假定整個系統只有沿x方向的一個自由度，用x表示。

給出了一些數值分析以驗證理論結果。在分析過程中，研究了系統的特點，振動系統的參數為：k1x＝100kn/m，k2x＝8000kn/m，m1＝1500kg，m2＝10kg，m0＝10kg，r＝0.15m，ξ2x＝0.02，ξ1x＝0.07。根據參數，ω0和ω1的值易得，ω0≈134rad/s，ω1≈74rad/s。另外，三個電動機的類型是相同的(三相鼠籠，50hz，380v，6極，0.75kw，額定速度980r/min)，并且電動機的參數：轉子電阻rr＝3.40ω，定子電阻rs＝3.35ω，互感lm＝164mh，轉子電感lr＝170mh，定子電感ls＝170mh，f1＝f2＝f3＝0.05。

1)穩態下的幅頻特性

基于式(8)～(9)，頻率-振幅曲線如圖5所示。從圖5中可以清楚地看出，三條曲線的趨勢是相同的，曲線都可以分為三部分，它們分別表示兩個剛體的三種運動狀態：(i)當偏心轉子運動頻率滿足ω<ω1，剛體a與剛體b之間的相對位移的幅度為零；(ii)當偏心轉子運動頻率滿足ω1<ω<ω0的條件時，剛體b的剛體a之間相對位移的振幅隨著外激頻率的增加而增加；(iii)當偏心轉子運動頻率滿足ω>ω0，兩個剛體的運動關系與在ω<ω1的條件下相同，它們是相對靜態的。在工程中，一般狀態(ii)滿足工作要求。

2)動態特性的討論

在上述分析中，定義了系統的同步能力系數ζij(ij＝12,23,13)，ζij是τcijmax和τamax之間的比值，其中τcijmax是三個偏心轉子的無量綱耦合力矩的最大值，τamax是三個電動機平均無量綱負載力矩。通常,ζij也稱為廣義動態對稱系數(cgds),它取決于振動系統的參數。在分析過程中，cgds越好，振動系統的同步能力越強。

根據式(18)～(24)可以得到如圖4所示的cgds曲線。圖6所示的曲線描述了對于不同的ηi(i＝1，2，3)，τcijmax隨著激勵頻率ω的變化。在圖6中，可以清楚地發現，當ω接近ω1或ω0時，cgds將突然減小。τcijmax的這種變化可以表明當激勵頻率ω等于ω1或ω0時，三個任意偏心轉子對的無量綱耦合力矩最大值達到最小。此外，從圖7中還可以清楚地看到，當ω接近ω1或ω0時同步能力最弱。分析可知，ω1和ω0分別是振動系統的兩個固有頻率，當ω等于ω1或ω0時，系統實現共振，同步能力弱。從圖7中的cgds的變化，容易發現振動系統打的廣義動態對稱性：(a)當η1＝η2＝η3＝1時，三個偏心轉子的質量相同，我們可以認為三個偏心轉子是對稱的，并且同步能力相同，(b)當η1＝η2＝1>η3＝0.6時，偏心轉子a和b的質量是相同的，換句話說，偏心轉子a和b是對稱的，因此cgds滿足(c)當η1＝1>η2＝0.8>η3＝0.6時，三個偏心轉子彼此不同，并且cgds滿足

3)同步狀態下的穩定相位差的討論

在振動系統同步狀態的分析過程中，穩定相位差的研究是必不可少的。當振動系統穩定運行時，三個電動機的輸出電磁轉矩分別相等。換句話說，在振動系統滿足同步判據和穩定性判據的條件下，三個電動機的輸出電磁轉矩的差值為零(即δt012＝δt023＝0)。基于此，考慮公式(15)，通過改變外激頻率ω的值，可以得到穩定的相位差的值，振動系統穩定相位差與外激頻率之間的關系曲線如圖5所示。

在圖8中，隨著ω的增加，穩定相位差值可以分為兩組，i和ii，然而，可以清楚地看到，i和ii的結果是相反的，考慮到動力學模型的對稱性，其可被看作為是一組穩定相位差。從圖8(a)，(b)，(c)可以看出，偏心轉子的穩定相位差值可以分為三個區域：

(i)z0<z1<1(即ω<ω1<ω0)。在該情況下，考慮到當ω非常小時(通常，ω≤25rad/s)振動系統不穩定，因此該區域可以忽略。在ω>25rad/s的情況下，根據圖8所示，當η1＝η2＝η3＝1時，三個偏心轉子相同，穩定相位差值滿足當η1＝η2＝1和η3＝0.6時，偏心轉子a和b是相同且對稱的，偏心轉子1與3，2與3之間的穩定相位差相等·，并且穩定相位差值滿足根據結果，可以得知當三個偏心轉子對不同時，在η1＝1,η2＝0.8和η3＝0.6的情況下有基于不同ηi(i＝1,2,3)下的穩定相位差值，可以發現三個偏心轉子實現了力的平衡。根據結果，可以得出，在這種情況下，兩個剛體隨著時間的推移而趨于靜止。

(ii)z0<1<z1(即ω1<ω<ω0)。在工程中，可以在該區域中選擇工作點。如圖8所示，不同ηi下的穩定相位差值在零附近，并且具有廣義動態對稱性。在η1＝η2＝η3＝1的條件下，三個偏心轉子是對稱的，穩定相位差值都為零，而在η1＝η2＝1和η3＝0.6的條件下，偏心轉子a和b是對稱的，當三個偏心轉子對不同時，穩定相位差值隨著ω變化不在恒為零。

(iii)1<z0<z1(即ω1<ω0<ω)。該情況下振動系統的運動狀態與z0<z1<1時的運動狀態相同。

4)同步狀態穩定性的討論

根據理論分析，三個電動機以ωm0的速度(ωm0等于外激頻率ω)實現同步穩定運轉，對于不同的ω，系統的同步穩定性是不一樣的。基于式(34)和式(35)，定義了h為振動系統的同步穩定性系數，h隨外激頻率的變化趨勢如圖9所示。從圖9中可以看出，對于不同的ηi，系統的同步穩定能力系數近似相等。圖中可以清楚地看到，曲線在點ω0上突變，而在ω1的點上變化緩慢。另外，在z0<z1<1的情況下，h的值小于零并且接近于零，這表示此時振動系統的同步穩定性非常弱。

5)穩態的相位滯后角的討論

為了分析剛體a和b之間的運動關系，將討論兩個剛體相對于偏心轉子的相位滯后角。根據式(10)，ηi對相位滯后角的影響非常小，忽略ηi的影響，在η1＝η2＝η3＝1時，相位滯后角γxi(i＝1，2)和外激頻率ω的關系曲線如圖10所示。從圖10可以看出，γx2-γx1的曲線可以分為兩組：(1)當γxi(i＝1，2)時，有γx2-γx1≈360°，兩個剛體在這種情況下以同相位運行；(2)當ω>ω1，有γx2-γx1≈180°，此時兩個剛體以反相位運行。

仿真模擬實驗

為了進一步分析數值結果，通過runge-kutta法得到三組仿真結果。振動系統和電動機的參數在上面部分已列出。在本節中，為了獲得當ω位于不同區域時系統的運動狀態，頻率比z0和z1可以通過改變彈簧剛度k2x而得到。同時，在每組中給出兩個仿真結果以進行比較。

1)z0<z1<1

圖11和圖12分別展示了在三個偏心轉子相同或不同的條件下系統的響應。從圖11(a)可以看出，同步旋轉速度約為983r/min，并且滿足彈簧剛度k2x＝80000kn/m，則頻率比z0≈0.24，z1≈0.45。通過改變偏心轉子的質量比ηi(i＝1，2，3)，另一組仿真結果也可以得到，如圖12。此外，在兩組仿真的過程中，電動機2在25s時受到π/3的干擾。

從圖11和圖12可以清楚地看到穩定相位差值滿足：η1＝η2＝η3＝1時2α1＝2α2＝120°；η1＝1，η2＝0.8，η3＝0.6時有2α1≈143.2°，2α2≈88.7°。此外，剛體的位移接近于零，換句話說，兩個剛體靜止。在圖11中，16s之后，偏心轉子對以穩定的相位差旋轉。在25s時，π/3的擾動被加到電動機2上，三個偏心轉子之間的相位差在短時間內出現波動，并且2α1，2α2隨時間的推移恢復到120°。此外，在圖12中，相位差的變化規律與圖11中的相同，兩個剛體之間的相對位移在25s時出現短時間的增加，后隨著時間的推移趨于零。在圖11中，還可以注意到，在大約16s之前，運動的狀態是不穩定的，因此這段時間可以被稱為過渡區。此外，對比數值結果，可以發現仿真結果的穩定相位差值對應于圖7(a)，(c)中的和而兩個剛體相對運動振幅對應于圖5中的點a，與數值結果相比，仿真結果有微小的差異。作者認為，導致這種現象的因素是系統的阻尼。

2)z0<1<z1

在仿真過程中，為了獲得相同的頻率比，兩個仿真的彈簧剛度k2x取值不同，η1＝η2＝η3＝1時k2x＝5000kn/m，η1＝1，η2＝0.8，η3＝0.6時k2x＝8000kn/m。根據系統參數和仿真結果，求得頻率比：z0≈0.63，z1≈1.15。圖13和圖14分別顯示了η1＝η2＝η3＝1和η1＝1,η2＝0.8，η3＝0.6時的仿真結果。和上一組仿真一樣，電動機2在15秒時受到π/3的擾動。

如圖13和圖14所示，穩定相位差值滿足：η1＝η2＝η3＝1時2α1＝2α2＝0°；η1＝1，η2＝0.8，η3＝0.6時有2α1≈-5.8°，2α2≈-10.5°。在η1＝η2＝η3＝1的情況下，剛體a的振幅為約7mm，剛體b的振幅為約14mm，同時兩個剛體相對位移的振幅約為21mm。此外，當η1＝1，η2＝0.8，η3＝0.6時，兩個剛體的相對位移的振幅接近15.9mm。

對比圖7(a)，(b)，仿真結果的穩定相位差值對應于圖7(a)，(c)中的和兩個剛體之間的相對位移的振幅分別對應于圖5中的b和d點。將數值結果與仿真結果進行比較，可以發現穩定相位差的仿真結果差異較大。針對這種現象，作者認為，由于阻尼的影響，系統的負載增加，為了平衡系統的負載，感應電動機將通過增加穩定相位差來產生足夠的耦合轉矩。

3)1<z0<z1

改變彈簧剛度k2x＝3000kn/m，在15s時給電動機加π/3的擾動上，此后，在不同質量比下的仿真結果如圖15和圖16所示。相比于z0<z1<1時的仿真結果，當振動系統以穩定相位差運行時，兩種狀態下的穩定相位差和位移是相同的。另外，此時仿真得出的穩定相位差值對應于圖11(a)，(c)中的和兩個剛體之間的相對位移的振幅對應于圖5中的點e。基于力學分析，在z0<z1<1和1<z0<z1的狀態下，三個偏心轉子對實現了力的平衡。

總結

基于以上的數值分析和計算機仿真，得出以下幾點：

通過數值分析，獲得振動系統的同步判據和同步狀態下的穩定性判據，并定義了同步能力系數和穩定性能力系數。根據同步能力系數和穩定性能力系數曲線，振動系統的同步能力和同步狀態下的穩定性能力在共振點ω1和ω0處最弱。通過比較外激頻率和兩個固有頻率的值，振動系統的運動狀態可以分為三個區域：(i)亞共振狀態(即ω<ω1)；(ii)近亞共振狀態(即ω1<ω<ω0)；(iii)超共振狀態(即ω>ω0)。

根據數值分析和計算機仿真結果，當系統穩定運行時，剛體在亞共振和超共振下的運動狀態是類似的，并且此時三個偏心轉子實現力的平衡，因此兩個剛體是靜止的。在近亞共振狀態下，剛體的運動類型為直線往復運動，穩定相位差區域為(-π/2,π/2)，兩個剛體以反相位運行。

實際工程上，在設計振動機的過程中，為了使振動機正常工作并執行其功能，工作點只能選擇在近亞共振狀態下。通常，當偏心轉子相同時，振動機工作效率是最好的。