本發明涉及非平穩信號的時頻分析領域，尤其是一種基于非線性模式分解和自適應最優核的時頻分析方法。

背景技術：

一個好的時頻分析方法在非平穩信號的估計分析中的作用不言而喻。信號本身具有很多屬性，而對于信號估計，頻域特性是很重要的屬性。

目前有很多信號處理和估計的方法，最經典的當然是傅立葉變換，它可以反映信號的頻率特性，傅立葉變換對于平穩信號擁有良好的頻域分辨能力，變換后可以得到信號的頻譜，但是傅立葉變換丟失了時間信息，即各個頻譜出現的時間并不知道，所以傅立葉變換不適合處理非平穩信號。對于實際環境里的非平穩信號，常用的線性時頻表示方法有短時傅里葉變換、小波變換、S變換等，但是它們的時頻精度有待提高；而Wigner-Ville分布、Cohen類時頻分布等雙線性時頻分布雖然具有較高的時頻精度，但卻不可避免地在計算過程中引入了交叉項。

經驗模態分解(Empirical Mode Decomposition，EMD)可將復雜信號分解為一系列本征模函數(Intrinsic Mode Function，IMF)。盡管EMD在抑制多分量信號的交叉項上有著不俗的表現，但是其缺點也很明顯，抗噪性能差，并且會因為不連續信號或者噪聲的存在而帶來模態混疊現象。為了克服EMD的缺點，出現了一種基于噪聲輔助的分析方法，叫做集合經驗模態分解(Ensemble Empirical Mode Decomposition，EEMD)。雖然EEMD在抗噪性能上要比EMD提升了一些，但是仍然達不到期望值。

時頻表示(Time-Frequency Representation，TFR)是一種十分有效的瞬時頻率估計方法，尤其是對于多分量信號。一般的TFR方法只有固定的窗函數或核函數，因此它們只對某一類信號的處理效果比較好。自適應最優核時頻表示(AOK TFR)是一種基于信號的瞬時頻率估計方法，采用可以隨著信號變化而變化的徑向高斯核函數，所以，AOK具有較好時頻聚焦性能和抑制交叉項能力。

EMD+AOK可以在分析多分量信號的時候減小交叉項的影響，但是對噪聲過于敏感。EEMD+AOK可以一定程度上提高抗噪性能，但是還遠遠不夠。

非線性模式分解(Nonlinear Mode Decomposition，NMD)可以將信號分解為一系列的有物理意義的非線性模式分量，具有很強的噪聲魯棒性。它是將時頻分析、數據替代檢驗以及諧波鑒別等多種方法融合起來的一種新型算法。然而，通過NMD分解得到的非線性模式分量并不是像IMF一樣的單分量，需用AOK方法的核函數能自適應隨信號的變化而變化的特點來進行優化。

基于NMD和AOK的新的時頻表示方法，不僅利用了NMD對多分量信號有效的分解性能，同時還繼承了AOK的優秀時頻聚焦性能和有效抑制交叉項的能力，解決了EMD+AOK和EEMD+AOK的抗噪性能差以及仍含有一定量的交叉項的問題。

技術實現要素：

發明目的：為解決上述技術問題，本發明提供一種基于非線性模式分解和自適應最優核的時頻分析方法，采用非線性模式分解(Nonlinear Mode Decomposition，NMD)把待處理信號分解為一系列非線性模式分量，抑制噪聲的干擾；然后將得到的各信號分量經過自適應最優核(AOK)分析方法處理抑制交叉項，由于自適應最優核的分析方法(AOK)能自動跟蹤分析信號的變化，核函數能根據信號的變化而自適應變化，對不同的信號產生的核函數總是最優的，所以其時頻分析性能比較好。

技術方案：為實現上述技術效果，本發明提供的技術方案為：

一種基于非線性模式分解和自適應最優核的時頻分析方法包括步驟：

(1)定義待處理信號為s(t)，s(t)的采樣頻率為f_s、數據長度為N；采用非線性模式分解法將待處理信號s(t)分解為一組非線性模式分量，即：

其中，c_i(t)為s(t)的第i個非線性模式分量，n(t)表示噪聲；

(2)對步驟(1)分解出的各非線性模式分量采用自適應最優核分析方法進行分析，包括步驟：

(2-1)構建徑向高斯核函數

式中，表示用于控制徑向高斯函數在徑向角方向的擴展函數；

(2-2)以得到隨著信號自適應變化的最優核為目標問題，構建優化問題模型為：

設置優化問題模型的約束條件為：

其中，為第i個非線性模式分量c_i(t)在極坐標下的模糊度函數，β為最優核的體積；在直角坐標系中的表達式為：

其中，A_i(t，θ，τ)為在直角坐標系中的映射量，s^*(t)，w^*(u)是s(t)，c_i(t)，w(u)的共軛復數形式；窗函數w(u)為以t的中心，寬度為2T的對稱菱形窗函數，且|u|＞T時，w(u)＝0，變量τ和θ是一般模糊域{τ，u}的參數，|τ|＜2T；

(2-3)根據A_i(t，θ，τ)求解優化問題模型，得到非線性模式分量c_i(t)的最優核函數Φ_(i)opt(t，θ，τ)；

(2-4)計算非線性模式分量c_i(t)的自適應最優核的時頻表示為：

式中，為非線性模式分量c_i(t)在t時刻的能量值；

(3)根據步驟(2)得到的所有非線性模式分量的自適應最優核的時頻表示，計算時頻分析的結果為：

進一步的，所述步驟(1)中采用非線性模式分解法將待處理信號s(t)分解為一組非線性模式分量的方法包括步驟：

(1-1)計算信號s(t)的小波變換表達式W_s(ω，t)：

其中，是s(t)的傅立葉變換，即s⁺(t)是s(t)信號的正頻率部分，是小波函數，與互為傅立葉變換對，且滿足條件ψ^*(t)，分別是ψ(t)，的共軛復數；ω_ψ表示小波峰值頻率，ω_ψ＝1，f₀為分辨率參數，用來權衡在變換過程中時間和頻率的分辨率；

(1-2)判斷步驟(1-1)計算得到的小波變換是否為s(t)的最佳時頻表示；若判斷結果為否，則計算信號s(t)的加窗傅里葉變換表達式G_s(ω，t)：

其中，g(t)是加窗傅里葉變換的窗函數，為g(t)的傅里葉變換，滿足以下條件：

且

(1-3)找出信號s(t)最佳時頻表示的所有的脊曲線，并用脊方法重構諧波分量，其中，第h次諧波分量為：

x^(h)(t)＝A^(h)(t)cosφ^(h)(t)，h∈[1，2，…，N]

式中，A^(h)(t)、φ^(h)(t)分別是第h次諧波分量的幅度和相位；v^(h)(t)是第h次諧波分量的頻率，y^(h)(t)≡φ′^(h)(t)；φ′^(h)(t)為φ^(h)(t)對時間t的導數；N表示諧波分量的最高次數，即數據長度；

(1-4)利用抗噪性替代檢驗方法對提取出的諧波分量的真偽進行鑒別，篩選出所有的真實的諧波分量，

(1-5)將所有的真實的諧波分量相加，得到一個非線性模式分量c₁(t)；

(1-6)從原信號s(t)中減掉非線性模式分解得到的c₁(t)，并且對殘余分量重復步驟1-1到步驟1-6，得到所有的各個非線性模式分量c_i(t)；

最終，原目標信號s(t)可以表示為：

式中，n(t)表示噪聲。

進一步的，所述步驟(1-3)中找出信號s(t)最佳時頻表示的所有的脊曲線的方法為：

在時刻t_i，找出h個極大值點，并將找出的h個極大值點相連，形成時刻t_i的脊曲線為：

上式中i＝1，2，…，N，N為數據長度；H_s(ω，t)是信號s(t)的最佳時頻表示，即為W_s(ω，t)或G_s(ω，t)；H_s(ω，t)中找出的所有時刻的脊點連線，即構成N條脊曲線。

進一步的，所述步驟(1-3)中用脊方法重構h次諧波分量x^(h)(t)＝A^(h)(t)cosφ^(h)(t)包括以下步驟：

若待處理的信號s(t)最佳時頻表示是小波變換，則

若待處理的信號s(t)最佳時頻表示是加窗傅立葉變換，則

式中，和是通過拋物線插值而得到的改進的離散化影響因子。

進一步的，所述步驟(1-4)中篩選真實的諧波分量的方法包括步驟：

(1-4-1)構建辨識統計量D(α_A，α_ν)，用于衡量各個諧波分量的幅值和頻率的有序度；D(α_A，α_v)的表達式為：

式中，和分別表示A^(h)(t)和v^(h)(t)的譜熵；α_A，α_v為權值系數；

(1-4-2)為原信號s(t)創建N_s個傅立葉變換替代數據；其中，第j個傅立葉變換替代數據的表達式為：

(1-4-3)計算每一個傅立葉變換替代數據的最佳時頻表示公式，并分別從其中提取出各次諧波分量，計算出各個傅立葉變換替代數據對應的辨識統計量為：

定義顯著性水平指標式中為滿足D_s＞D₀的替代數據的個數；D₀為原信號的h次諧波的有序度；

設置顯著水平指標為p，當存在x個替代數據滿足D_s＞D₀且x≥p×N_s時，判定對應的諧波分量不是噪聲；否則，判定對應的諧波分量是噪聲；

(1-4-4)計算諧波之間相關度的綜合度量值

其中，

式中，w_A，w_φ，w_v代表的權值，ρ^(h)為幅度和相位一致性分配相等的權值ρ^(h)≡ρ^(h)(1，1，0)；

(1-4-5)定義綜合度量值的閾值

(1-4-6)當一個諧波分量滿足ρ^(h)≥ρ_min且顯著性水平指標p≥95％時，判定此諧波分量通過檢驗，為真實的諧波分量。

進一步的，所述步驟(1-4-3)中判斷一個替代數據是否滿足D_s＞D₀的方法為：

選取任意三組不同值的參數(α_A，α_v)，分別計算三組參數對應的辨識統計量值，若存在任意一個辨識統計量值大于D₀，則判定該替代數據滿足D_s＞D₀。

有益效果：與現有技術相比，本發明具有以下優勢：

NMD方法不僅對于高斯白噪聲具有良好的抑制效果，同時也能夠有效抑制其他類型的噪聲信號，具有很強的噪聲魯棒性和廣泛的適應性；然而，通過NMD分解得到的非線性模式分量并不是像IMF一樣的單分量，需用AOK方法的核函數能自適應隨信號的變化而變化的特點來進行優化，AOK方法能夠有效地、自適應地跟蹤非平穩信號的變化。本發明基于NMD和AOK的新的時頻表示方法，不僅利用了NMD對多分量信號有效的分解性能，同時還繼承了AOK的優秀時頻聚焦性能和有效抑制交叉項的能力，解決了EMD+AOK和EEMD+AOK的抗噪性能差以及仍含有一定量的交叉項的問題。

附圖說明

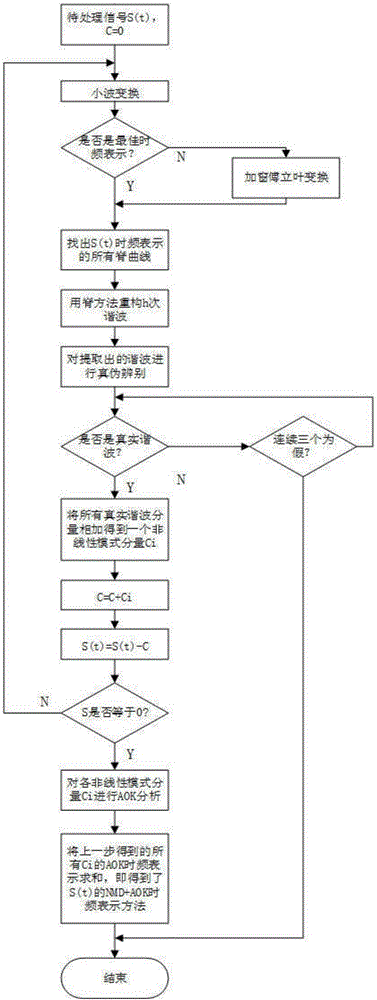
圖1為本發明的流程圖。

具體實施方式

以下以一個多分量非平穩仿真信號為例，詳細說明本發明的實施方式以及優越性。

假設s(t)為一個含有高斯白噪聲的多分量信號：

s(t)＝s_d(t)+n(t)

s_d(t)＝cos(20πt)+sin(200πt)+sin(400πt)+sin(100π(t-0.5)²)

式中，n(t)表示高斯白噪聲；s_d(t)為理想的多分量信號。設置采樣頻率為1kHz，采樣時間1s，數據長度為1000。設置窗長度2T＝128，核函數體積限制為β＝5。

本發明的流程如圖1所示，包括以下步驟：

步驟A：準備待處理的信號s(t)，其采樣頻率為f_s、數據長度為N；

步驟B：對信號s(t)進行NMD分析；

步驟B-1：計算信號s(t)的小波變換(Wavelet Transform，WT)W_s(ω，t)，

其中，是s(t)的傅立葉變換，即s⁺(t)是s(t)信號的正頻率部分，ψ(t)是小波函數，與互為傅立葉變換對，且滿足條件ψ^*(t)，分別是ψ(t)，的共軛復數。表示小波峰值頻率。

ω_ψ＝1

其中，f₀是一個分辨率參數，用來權衡在變換過程中時間和頻率的分辨率(通常情況下默認為1)。時間分辨率高則頻率分辨率降低，反之亦然。

步驟B-2：檢查步驟B-1得到的小波變換W_s(ω，t)是否為信號s(t)的最佳時頻表示，若不是，則采用加窗傅里葉變換(Windowed Fourier Transform，WFT)G_s(ω，t)，WFT定義為：

其中，g(t)是WFT的窗函數，為g(t)的Fourier變換，滿足條件：選擇高斯窗作為WFT的窗函數，其表達式為：

步驟B-3找出信號s(t)最佳時頻表示的所有的脊曲線這里是第h次諧波的脊曲線。所謂的脊曲線就是時頻圖上一些局部極大值點所連接而成的曲線。各個極大值點就叫脊點。

在時刻t_i，利用下式算法，可以找出h個極大值點：

上式中i＝1，2，…，N，N為數據長度。H_s(ω，t)是信號s(t)的最佳時頻表示，即為W_s(ω，t)或G_s(ω，t)。

將H_s(ω，t)中找出的所有時刻的脊點連線，即構成H條脊曲線。

步驟B-4：用脊方法重構第h次諧波分量為x^(h)(t)＝A^(h)(t)cosφ^(h)(t)，其中A^(h)(t)、φ^(h)(t)分別是第h次諧波分量的幅度和相位，ν^(h)(t)是第h次諧波分量的頻率，ν^(h)(t)≡φ′^(h)(t)，φ′^(h)(t)為φ^(h)(t)對時間t的導數。

若待處理的信號s(t)的最佳時頻表示為W_s(ω，t)，那么可以通過以下公式計算得到信號s(t)的第h次諧波分量x^(h)(t)。

若待處理信號s(t)的最佳時頻表示為G_s(ω，t)，那么計算s(t)的h次的諧波相關分量x^(h)(t)為：

式中，和是通過拋物線插值而得到的改進的離散化影響因子。

步驟B-5：利用抗噪性替代檢驗方法對提取出的諧波分量的真偽進行鑒別，篩選出所有的真實的諧波分量，并且當連續三個諧波分量被判斷為假時停止分解過程。包括以下步驟：

(1)從TFR中提取出諧波分量并計算出對應的辨識統計量D(α_A，α_v)；

提取出的每一個諧波分量的幅值A^(h)(t)和頻率ν^(h)(t)的有序度可以用其譜熵和來定量地衡量，辨識統計量D和譜熵Q定義如下：

其中，α_A，α_v是計算D(α_A，α_v)的權值系數。

(2)為原信號s(t)創建N_s個傅立葉變換替代數據；

令的幅值保持不變，相位變為均勻分布在[0，2π)上的N_s個隨機相位這種隨機分布的每個相位對應的傅里葉反變換即為s(t)的一個傅立葉變換替代數據s′_j(t)。

這里j＝1，2，…，N_s。

(3)計算與每一個替代數據相關的TFR，并分別從其中提取出各次諧波分量，從而計算出各個替代數據對應的辨識統計量

定義顯著性水平指標式中是D_s＞D₀的替代數據的個數；D₀為原信號的h次諧波的有序度。

假設創建N_s個替代數據并且顯著水平指標設置為p，即至少有p×N_s個替代數據滿足D_s＞D₀才能認為該分量不是噪聲，從而繼續分解過程。

判斷一個替代數據是否滿足D_s＞D₀的方法為：選取任意三組不同值的參數(α_A，α_v)，分別計算三組參數對應的辨識統計量值，若存在任意一個辨識統計量值大于D₀，則判定該替代數據滿足D_s＞D₀。

(4)計算諧波之間相關度的綜合度量值

其中，

式中，w_A，w_φ，w_v代表的權值，在這里，默認使用ρ^(h)≡ρ^(h)(1，1，0)為幅度和相位一致性分配相等的權值，且對頻率一致性不分配權值。

(5)為了減少對真實諧波分量的錯誤判斷，定義綜合度量值的閾值

(6)當一個諧波分量滿足ρ^(h)≥ρ_min且顯著性水平指標p≥95％時，則認為此諧波分量通過檢驗，為真實的諧波分量。

步驟B-6：將所有的真實的諧波分量相加從而得到一個非線性模式分量c₁(t)。

步驟B-7：從原信號s(t)中減掉非線性模式分解得到的c₁(t)，并且對殘余分量重復步驟B-1到步驟B-6得到所有的各個非線性模式分量c_i(t)。

最終，原目標信號s(t)可以表示為：

式中，n(t)表示噪聲。

步驟C：對NMD方法分解出的各個非線性模式分量c_i(t)進行AOK分析，其過程如下：

步驟C-1：首先選擇徑向高斯核函數，其定義如下：

式中，表示用于控制徑向高斯函數在徑向角方向的擴展函數。

步驟C-2：為了得到隨著信號自適應變化的最優核，應求解以下有約束的優化問題。

約束條件為：

其中，是極坐標下的模糊度函數，為每個非線性模式分量對應的β是最優核的體積。

在直角坐標系中的定義A_i(t；θ，τ)為：

其中，s^*(t)，w^*(u)是s(t)，c_i(t)，w(u)的共軛復數形式；窗函數w(u)為以t的中心，寬度為2T的對稱菱形窗函數，且|u|＞T時，w(u)＝0；變量τ和θ是一般模糊域{τ，u}的參數，且|τ|＜2T。

步驟C-3：把代入步驟C-2中的(4)，(5)式，可以通過求解這個有約束的優化問題得到一個最優核函數它與短時模糊函數一樣會隨著時間變化。

步驟C-4：計算當前時間點(t時刻)某個非線性模式分量c_i(t)的自適應最優核的時頻表示AOK TFR_i：

式中，為信號某一分量c_i(t)在某一個t時刻的能量值。

步驟C-5：重復步驟C-1至步驟C-4，得到所有分解出的非線性模式分量的自適應最優核時頻表示。

步驟D：將得到的所有信號分量的AOK TFR_i(即)求和，得到最終的時頻分析的結果P_NMD-AOK(t，ω)：

由上式即可以最終得到NMD+AOK時頻分析的結果。

將本發明所提供的的技術方案與現有技術相比，可以得到以下分析結果：

只用AOK方法會產生一定量的交叉項，并且抗噪性能很差；EMD+AOK和EEMD+AOK方法能在一定程度上抑制交叉項，但是仍然對噪聲過于敏感；而本發明所采用的NMD+AOK方法不論是在去除噪聲還是抑制交叉項方面，明顯優于其他的幾種方法。

以上所述僅是本發明的優選實施方式，應當指出：對于本技術領域的普通技術人員來說，在不脫離本發明原理的前提下，還可以做出若干改進和潤飾，這些改進和潤飾也應視為本發明的保護范圍。