本發明涉及工程巖體細觀時效破裂分析技術領域，具體地指一種考慮彎矩貢獻因子的二維時效破裂模型。

背景技術：

深部巖體工程開挖后的失穩與破壞往往不是在開挖后立刻發生的，一般都存在著明顯的變形破裂時效性和災變(巖爆、大變形等)的滯后性，嚴重危害工程的施工安全與長期運營。目前，在細觀方面的時效力學研究成果相對較少。劉寧等對錦屏大理巖破裂的時間效應進行了試驗和數值分析(深埋大理巖破裂擴展時間效應的顆粒流模擬，巖石力學與工程學報，2011,Vol.30No.10:1989-1996)；孫金山等應用蠕變細觀力學模型對錦屏大理巖短期和長期強度特征進行了數值研究(錦屏大理巖蠕變損傷演化細觀力學特征的數值模擬研究，巖土力學，2013,Vol.34No.12:3601-3608)。這些都是以離散元中平行粘結模型(Parallel-Bonded Model，PBM)為基礎，根據驅動應力和裂紋擴展速度間的關系來描述巖石細觀層面上的時效破裂。但是，這類平行粘結模型存在很多不足之處：首先，平行粘結斷裂之后，顆粒之間只考慮滑動摩擦力，沒有考慮斷裂顆粒間的接觸方式，不符合巖體破裂后的不同細觀顆粒在外荷載下的運動方式；其次，顆粒間的剪切破裂準則是一條與平行粘結正應力平行的水平直線，也即這種剪切破裂準則與平行粘結正應力狀態無關，只要平行粘結剪切應力大于或等于固定平行粘結剪切破裂強度，顆粒間即可發生剪切破裂，無法體現巖體中不同平行粘結正應力具有不同平行粘結剪切破裂強度的客觀事實；另外，對于巖體這類摩擦粘結性材料，上述這種平行粘結模型并沒有考慮粘結力矩的差異作用對接觸破壞的影響，將粘結力矩的貢獻度對不同巖性的影響均視為一致，夸大了粘結力矩對巖體的破壞作用。

技術實現要素：

本發明的目的在于針對上述缺陷，提出了一種考慮彎矩貢獻因子的二維時效破裂模型，本發明適應于應力和裂紋擴展速度之間的關系符合指數型的這類巖體，對于平面狀態下這類深部巖體工程的圍巖長期穩定性預測、評價以及優化設計提供技術支持。

本發明的目的是通過如下措施來達到的：考慮彎矩貢獻因子的二維時效破裂模型，其特殊之處在于，所述二維時效破裂模型適應于二維顆粒離散元、二維顆粒不連續變形分析方法、二維顆粒流形元；所述二維時效破裂模型包括考慮彎矩貢獻因子的二維平行粘結應力模式、考慮彎矩貢獻因子的二維平行粘結直徑時效劣化衰減模式、考慮彎矩貢獻效應且帶拉伸截止限的摩爾-庫倫時效破裂準則以及巖體時效破裂后考慮阻尼效應的二維線性接觸模型。

進一步地，所述考慮彎矩貢獻因子的二維平行粘結應力模式是指二維平行粘結正應力計算公式中設置了彎矩貢獻因子考慮彎矩對二維平行粘結正應力的貢獻程度；在上述公式中，為第i個巖體細觀顆粒二維平行粘結的正應力，分別為第i個接觸的巖體細觀顆粒平行粘結法向力、切向彎矩；為巖體細觀顆粒二維平行粘結半徑，為彎矩貢獻因子，I為巖體細觀顆粒二維平行粘結的慣性矩，A為巖體細觀顆粒二維平行粘結面積，i依次為第一個至最后一個巖體細觀顆粒平行粘結數。

更進一步地，所述考慮彎矩貢獻因子的二維平行粘結直徑時效劣化衰減模式包括所述考慮彎矩貢獻因子的二維平行粘結時效劣化衰減模式，在巖體細觀顆粒二維平行粘結時效劣化衰減時，設置了與考慮彎矩貢獻因子的平行粘結應力相關的指數型模式，這種指數型模式中的二維平行粘結直徑隨時間逐步劣化衰減，見平行粘結直徑公式式中，為考慮彎矩貢獻因子的二維平行粘結法向應力，為判斷巖體細觀顆粒二維平行粘結開始時效劣化衰減時的應力閥值，為巖體細觀顆粒二維平行粘結拉伸強度，為考慮彎矩貢獻因子的二維平行粘結應力比，β₁、β₂為控制巖體細觀顆粒平行粘結時效劣化的第一控制參數、第二控制參數，為巖體細觀顆粒二維平行粘結隨時間劣化衰減的直徑，為巖體細觀顆粒二維平行粘結未衰減時的直徑，e為自然常數，Δt為巖體細觀顆粒二維平行粘結時效衰減劣化的時間增量；設置了巖體細觀顆粒二維平行粘結面積和慣性矩時效劣化衰減模式，分別見平行粘結單位厚度為1時的平行粘結面積計算公式平行粘結單位厚度為1時的慣性矩計算公式其中，β為巖體細觀顆粒二維平行粘結直徑的指數型時效衰減因子，其計算公式見式中A'、I'、分別表示為巖體細觀顆粒二維平行粘結隨時間劣化衰減的平行粘結直徑、平行粘結半徑、平行粘結面積、平行粘結慣性矩、平行粘結直徑乘數，A、I、為巖體細觀顆粒平行粘結未衰減時的平行粘結直徑、平行粘結半徑、平行粘結面積、平行粘結慣性矩、平行粘結直徑乘數；同時按照這種二維指數型時效劣化衰減模式估算巖體細觀顆粒二維平行粘結破裂的初始時間步長，見公式其中，為第i個接觸的巖體細觀顆粒二維平行粘結直徑乘數，n_c為第一個巖體細觀顆粒二維平行粘結破裂所需的循環計算的次數，β_σ、β_τ分別為巖體細觀顆粒二維平行粘結拉伸強度對應的時效劣化因子、二維平行粘結剪切強度對應的時效劣化因子，i依次為第一個至最后一個巖體細觀顆粒平行粘結數，∞為無窮大。

更進一步地，所述考慮彎矩貢獻效應且帶拉伸截止限的摩爾-庫倫時效破裂準則是指在判斷巖體細觀顆粒二維平行粘結時效破裂時，采用所嵌入的考慮彎矩貢獻效應且帶拉伸截止限的摩爾-庫倫時效破裂強度準則來判斷，見公式

其中，f^s、fⁿ分別為巖體細觀顆粒二維平行粘結的時效剪切破裂準則、時效拉伸破裂準則，分別為巖體細觀顆粒二維平行粘結拉伸強度、抗剪強度，分別為第i個接觸的含指數型時間效應且考慮彎矩貢獻因子的巖體細觀顆粒二維平行粘結正應力、剪應力，為巖體細觀顆粒二維平行粘結的內摩擦角，為巖體細觀顆粒二維平行粘結的粘聚力，為巖體細觀顆粒二維平行粘結半徑，分別為第i個顆粒接觸的平行粘結法向力和切向力、平行粘結切向彎矩，為彎矩貢獻因子，i依次為第一個至最后一個巖體細觀顆粒平行粘結數；

在該準則的二維平行粘結應力中包含了指數型時間效應，見巖體細觀顆粒二維平行粘結直徑的時效衰減因子計算公式式中為巖體細觀顆粒二維平行粘結隨時間劣化衰減的直徑，為巖體細觀顆粒二維平行粘結未衰減時的直徑，為考慮彎矩貢獻因子的二維平行粘結應力比，為巖體細觀顆粒二維平行粘結法向應力，為判斷巖體細觀顆粒二維平行粘結開始時效劣化衰減時的應力閥值，為巖體細觀顆粒二維平行粘結的拉伸強度，Δt為巖體細觀顆粒二維平行粘結時效衰減劣化的時間增量，β₁、β₂分別為控制巖體細觀顆粒平行粘結時效劣化的第一控制參數、第二控制參數；

f^s大于等于0表示巖體細觀顆粒二維平行粘結剪切破裂，小于0表示巖體細觀顆粒二維平行粘結未發生剪切破裂；fⁿ大于等于0表示巖體細觀顆粒二維平行粘結拉伸破裂，小于0表示巖體細觀顆粒二維平行粘結未發生拉伸破裂。

更進一步地，所述巖體時效破裂后考慮阻尼效應的二維線性接觸模型是指巖體細觀顆粒平行粘結時效破裂后，通過二維線性接觸參考距離g_r設定了細觀顆粒二維線性接觸距離g_s，見巖體細觀顆粒二維線性接觸距計算公式其中，為巖體內部顆粒與顆粒二維線性接觸端a的坐標，為巖體內部顆粒與顆粒二維線性接觸端b的坐標，R^a、R^b分別為巖體細觀二維線性接觸端a的顆粒半徑和二維線性接觸端b的顆粒半徑；設置考慮巖體細觀顆粒間受力變形的二維線性接觸模式，在巖體顆粒之間設置考慮二維滑動摩擦線力的作用模式，巖體細觀顆粒間受力變形的二維線性接觸法向線性力計算公式取M_l＝1為相對矢量累加模式，取M_l＝0為絕對矢量累加模式，巖體細觀顆粒間受力變形的二維線性接觸切向線性力計算公式為其中，分別為巖體細觀顆粒間受力變形的二維線性接觸法向線性力、切向線性力，k_n、k_s分別為巖體細觀顆粒間受力變形的二維線性接觸法向、切向線性剛度，Δδ_n、Δδ_s分別為法向位移增量、切向位移增量，分別為初始法向力增量值和切向力增量值，為顆粒未滑動時的靜摩擦力，為巖體細觀顆粒滑動摩擦力，通過摩擦系數μ與乘積得到；同時設置二維接觸的阻尼模式，其中法向阻尼采用全法向模式M_d＝{0,2}和無拉伸模式M_d＝{1,3}兩種，通過公式計算，其中m_c為等效顆粒質量，按公式計算，切向阻尼采用全剪切模式M_d＝{0,1}和滑-剪模式M_d＝{2,3}，按照公式來計算，其中：分別為法向阻尼力、切向阻尼力，β_n為法向阻尼系數、β_s為切向阻尼系數，k_n為法向線性剛度、k_s為切向線性剛度，分別為法向速率、切向速率，F^*為巖體細觀顆粒線性接觸的全法向阻尼力，表達式為m_c為等效顆粒質量，m⁽¹⁾為二維線性接觸端1的巖體細觀顆粒質量，m⁽²⁾為二維線性接觸端2的巖體細觀顆粒質量。

更進一步地，所述第i個接觸的巖體細觀顆粒平行粘結法向力、切向彎矩的計算方法為：式中，為巖體細觀顆粒二維平行粘結法向剛度，為巖體細觀顆粒二維平行粘結法向位移增量，為巖體細觀顆粒二維平行粘結切向相對轉角增量，+＝為加法自反運算符，-＝為減法自反運算符，法向彎矩

更進一步地，所述巖體細觀顆粒二維平行粘結拉伸強度對應的時效劣化因子β_σ和剪切強度對應的時效劣化因子β_τ的計算公式分別為

其中，為巖體細觀顆粒二維平行粘結半徑，分別為第i個顆粒接觸的平行粘結法向力、平行粘結切向力、平行粘結切向彎矩，為彎矩貢獻因子，為巖體細觀顆粒二維平行粘結拉伸強度，為巖體細觀顆粒二維平行粘結的粘聚力，為巖體細觀顆粒二維平行粘結的內摩擦角，i依次為第一個至最后一個巖體細觀顆粒平行粘結數。

更進一步地，所述第i個接觸的含指數型時間效應且考慮彎矩貢獻因子的巖體細觀顆粒二維平行粘結正應力的計算公式為所述第i個接觸的含指數型時間效應的巖體細觀顆粒二維平行粘結剪應力的計算公式為

本發明提出的考慮彎矩貢獻因子的二維時效破裂模型，在平行粘結時效破裂之后，通過在顆粒之間嵌入考慮阻尼效應的二維線性模型來表達顆粒間的接觸方式，不僅可以考慮滑動摩擦作用，而且還可以考慮顆粒間的變形特性，符合巖體顆粒在平面狀態下的運動規律；其次，在平行粘結應力計算中引入彎矩貢獻因子，不僅考慮彎矩了對平行粘結正應力貢獻，而且還考慮了彎矩對巖體長期強度的影響；另外，在所構建的二維時效破裂模型中嵌入考慮彎矩貢獻效應且帶拉伸截止限的摩爾-庫倫時效破裂準則，該準則平行粘結應力中包含了指數型時間效應且增加了彎矩貢獻因子，不僅可以描述與平行粘結正應力相關時效剪切破裂強度的差異，還可以對時效拉伸破裂進行合理的表達，且考慮了彎矩對平行粘結時效破裂的影響，符合巖體在平面狀態下時效破裂的基本特征。本發明對于平面狀態下深部巖體工程圍巖長期穩定性預測、評價以及優化設計提供直接的技術支持。

本發明所提出的一種考慮彎矩貢獻因子的二維時效破裂模型結構，其有益效果和優勢主要體現在：

(1)本發明中通過在二維平行粘結正應力計算公式中設置彎矩貢獻因子，不僅考慮了彎矩對平行粘結正應力的貢獻程度，而且還考慮了彎矩對巖體長期強度的影響，同時減小巖體破裂過程中產生過強的能量沖擊波對鄰近區域造成的二次損傷，適合描述平面應力或平面應變條件下巖體的細觀力學破裂行為。

(2)本發明中通過構建考慮彎矩貢獻因子的二維平行粘結直徑時效劣化衰減模式，包括設置指數型與考慮彎矩貢獻因子的平行粘結應力相關的二維平行粘結直徑劣化衰減模式，設置平行粘結直徑隨著時間增加逐步劣化衰減模式，同時設置平行粘結的面積和截面慣性矩相應的時效劣化衰減模式。這種構建模式適合描述平面應力或平面應變條件下深部巖體的細觀力學時效破裂機制和響應規律。

(3)本發明中在所構建的二維時效破裂模型中，嵌入考慮彎矩貢獻效應且帶拉伸截止限的摩爾-庫倫時效破裂準則。在該準則平行粘結應力中包含指數型時間效應且增加了彎矩貢獻因子，不僅可以描述與平行粘結正應力相關時效剪切破裂強度的差異，還可以對時效拉伸破裂進行合理的表達，且考慮了彎矩對平行粘結時效破裂的影響，符合平面條件下巖體時效破裂模式。

(4)本發明中在所構建的二維時效破裂模型中，嵌入考慮阻尼效應的二維線性接觸模型結構，在巖體細觀顆粒平行粘結時效破裂后，通過指定二維接觸參考距離設定巖體顆粒間接觸距離，設置考慮巖體顆粒間受力變形的二維接觸模式以及在巖體顆粒之間設置考慮二維滑動摩擦的作用模式，同時設置二維接觸的阻尼模式，可合理描述平面應力或平面應變條件下深部工程巖體在時效破裂后的顆粒運動和受力特征。

附圖說明

圖1是本發明模型中巖體顆粒與顆粒接觸示意圖。

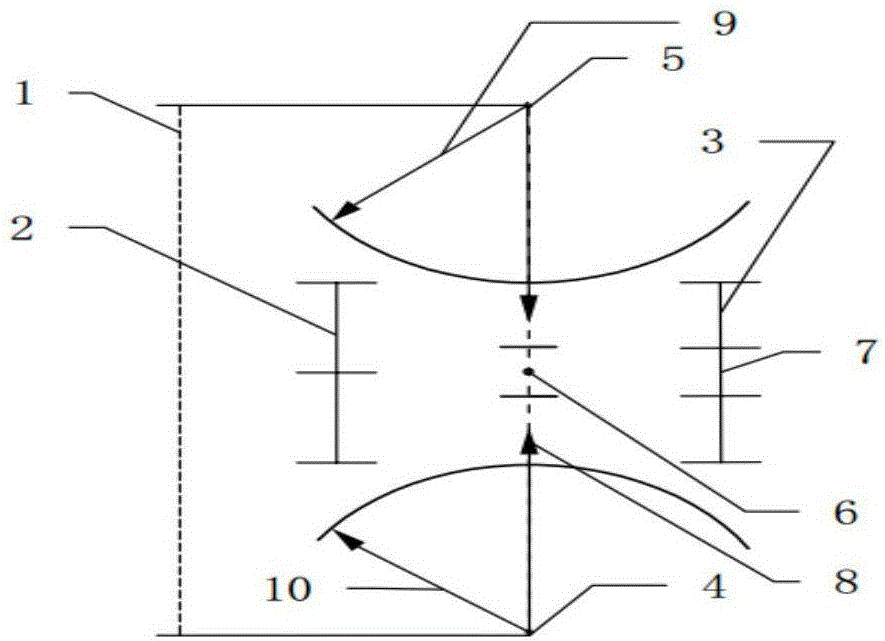
圖2是本發明模型中巖體顆粒與剛性墻接觸示意圖。

圖3是本發明模型中巖體顆粒重疊狀態示意圖。

圖4是本發明模型中巖體顆粒剛度計算示意圖。

圖5是本發明模型中線性切向力和切向位移示意圖

圖6是本發明中所構建的二維時效破裂物理模型示意圖。

圖7是本發明模型中線性平行粘結結構示意圖。

圖8是本發明模型中的考慮彎矩貢獻效應且帶拉伸截止限的摩爾-庫倫破裂準則示意圖。

圖9是本發明模型中直徑時效衰減示意圖。

圖10是本發明模型直徑時效衰減率對數與應力曲線示意圖。

圖11是本發明模型二維接觸面的法向和切向單位向量示意圖。

圖12是本發明模型結構構建流程示意圖。

圖13是本發明模型蠕變損傷分布圖。

圖14是本發明模型蠕變位移與時間關系曲線圖。

圖15是本發明模型不同力矩貢獻度的蠕變位移與時間關系曲線圖。

圖中：1代表巖體兩顆粒的中心距離d，2代表巖體兩顆粒間的半接觸距離，3代表巖體兩顆粒間的半參考距離g_r，4代表巖體顆粒a的坐標，5代表巖體顆粒b的坐標，6表面巖體顆粒接觸距離的中心坐標，7代表巖體顆粒表面接觸距離g_s，8代表巖體顆粒間的單位接觸法向量，9代表巖體顆粒a的半徑R^a，10代表巖體顆粒b的半徑R^b，11代表巖體顆粒接觸點的接觸重疊量U，12代表b(巖體顆粒或是邊界墻體)的剛度(法向、切向剛度統稱)k^b，13代表a(巖體顆粒或是邊界墻體)的剛度(法向、切向剛度統稱)k^a，14代表接觸點的等效剛度，15代表總位移增量ΔU_i，16代表初始法向力增量值，17代表初始接觸力矢量和，18代表初始切向力增量值，19代表所構建的二維時效破裂模型法向位移增量Δδ_n或20代表所構建的二維時效破裂模型切向位移增量Δδ_s或21代表平行粘結的拉伸強度22代表平行粘結法向剛度23代表線性接觸點的法向剛度K_n，24代表平行粘結切向剛度25代表平行粘結剪切強度，25.1代表為平行粘結的粘聚力，25.2代表平行粘結的內摩擦角26代表線性接觸點的切向剛度K_s，27代表滑動摩擦系數，28代表為線性接觸法向阻尼系數β_n，29代表線性接觸切向阻尼系數β_s，30代表平行粘結直徑(半徑)乘數31代表平行粘結直徑232代表考慮彎矩貢獻效應且帶拉伸截止限的摩爾-庫倫時效破裂準則，33代表第i個接觸的包含時間效應的平行粘結剪應力34代表第i個接觸的包含時間效應且考慮彎矩貢獻因子的平行粘結正應力35代表平行粘結時效衰減的半徑36代表平行粘結時效衰減的直徑37代表平行粘結未衰減時的直徑38代表平行粘結未衰減時的半徑39代表為對數更新率ln(γ)，40代表判斷巖體顆粒開始時效劣化衰減時的應力閥值41代表拉伸強度42代表考慮彎矩貢獻因子的平行粘結應力比43代表控制巖體細觀顆粒平行粘結時效劣化的第二控制參數β₂，44代表二維接觸面的法向向量n_n，45代表二維接觸面切向單位向量n_s。

具體實施方式

下面結合附圖和具體構建步驟及實施實例，對本發明模型進行詳細的闡述。實例說明僅是輔助用于本發明的理解，而不限定本發明的實際應用范圍。在閱讀了本發明以后，本領域的技術人員對本發明的各種等價形式的修改均屬于本發明所申請的權利要求所限定的范圍。

注：說明書中的所有的標號前面寫明了公式，如公式(1)，均為公式標號。

如圖1～圖11所示，本發明考慮彎矩貢獻因子的二維時效破裂模型適應于二維顆粒離散元、二維顆粒不連續變形分析方法、二維顆粒流形元；二維時效破裂模型包括考慮彎矩貢獻因子的二維平行粘結應力模式、考慮彎矩貢獻因子的二維平行粘結直徑時效劣化衰減模式、考慮彎矩貢獻效應且帶拉伸截止限的摩爾-庫倫時效破裂準則以及巖體時效破裂后考慮阻尼效應的二維線性接觸模型。

考慮彎矩貢獻因子的二維平行粘結應力模式是指二維平行粘結正應力計算公式中設置了彎矩貢獻因子考慮彎矩對二維平行粘結正應力的貢獻程度；

第i個接觸的巖體細觀顆粒平行粘結法向力的計算方法為：第i個接觸的巖體細觀顆粒平行粘結切向彎矩的計算方法為：

在上述公式中，為第i個巖體細觀顆粒二維平行粘結的正應力，分別為第i個接觸的巖體細觀顆粒平行粘結法向力、切向彎矩；為巖體細觀顆粒二維平行粘結半徑，為彎矩貢獻因子，I為巖體細觀顆粒二維平行粘結的慣性矩，A為巖體細觀顆粒二維平行粘結面積，i依次為第一個至最后一個巖體細觀顆粒平行粘結數，為巖體細觀顆粒二維平行粘結法向剛度，為巖體細觀顆粒二維平行粘結法向位移增量，為巖體細觀顆粒二維平行粘結切向相對轉角增量，+＝為加法自反運算符，-＝為減法自反運算符，法向彎矩

考慮彎矩貢獻因子的二維平行粘結直徑時效劣化衰減模式包括考慮彎矩貢獻因子的二維平行粘結時效劣化衰減模式，在巖體細觀顆粒二維平行粘結時效劣化衰減時，設置了與考慮彎矩貢獻因子的平行粘結應力相關的指數型模式，這種指數型模式中的二維平行粘結直徑隨時間逐步劣化衰減，見平行粘結直徑公式式中，為考慮彎矩貢獻因子的二維平行粘結法向應力，為判斷巖體細觀顆粒二維平行粘結開始時效劣化衰減時的應力閥值，為巖體細觀顆粒二維平行粘結的拉伸強度，為考慮彎矩貢獻因子的二維平行粘結應力比，β₁、β₂分別為控制巖體細觀顆粒平行粘結時效劣化的第一控制參數、第二控制參數，為巖體細觀顆粒二維平行粘結隨時間劣化衰減的直徑，為巖體細觀顆粒二維平行粘結未衰減時的直徑，e為自然常數，Δt為巖體細觀顆粒二維平行粘結時效衰減劣化的時間增量；設置了巖體細觀顆粒二維平行粘結面積和慣性矩時效劣化衰減模式，分別見平行粘結單位厚度為1時的平行粘結面積計算公式平行粘結單位厚度為1時的慣性矩計算公式其中，β為巖體細觀顆粒二維平行粘結直徑的指數型時效衰減因子，其計算公式見式中，A'、I'、分別表示為巖體細觀顆粒二維平行粘結隨時間劣化衰減的平行粘結直徑、平行粘結半徑、平行粘結面積、平行粘結慣性矩、平行粘結直徑乘數，A、I、為巖體細觀顆粒平行粘結未衰減時的平行粘結直徑、平行粘結半徑、平行粘結面積、平行粘結慣性矩、平行粘結直徑乘數；

同時按照這種二維指數型時效劣化衰減模式估算巖體細觀顆粒二維平行粘結破裂的初始時間步長，見公式其中，為第i個接觸的巖體細觀顆粒二維平行粘結直徑乘數，n_c為第一個巖體細觀顆粒二維平行粘結破裂所需的循環計算的次數，β_σ、β_τ分別為巖體細觀顆粒二維平行粘結拉伸強度對應的時效劣化因子、二維平行粘結剪切強度對應的時效劣化因子，i依次為第一個至最后一個巖體細觀顆粒平行粘結數，∞為無窮大。巖體細觀顆粒二維平行粘結拉伸強度對應的時效劣化因子β_σ和巖體細觀顆粒二維平行粘結剪切強度對應的時效劣化因子β_τ的計算公式分別為

其中，分別為第i個顆粒接觸的平行粘結法向力、平行粘結切向力、平行粘結切向彎矩，為巖體細觀顆粒二維平行粘結的粘聚力，為巖體細觀顆粒二維平行粘結的內摩擦角。

考慮彎矩貢獻效應且帶拉伸截止限的摩爾-庫倫時效破裂準則是指在判斷巖體細觀顆粒二維平行粘結時效破裂時，采用所嵌入的考慮彎矩貢獻效應且帶拉伸截止限的摩爾-庫倫時效破裂強度準則來判斷，見公式

其中，f^s、fⁿ分別為巖體細觀顆粒二維平行粘結的時效剪切破裂準則、時效拉伸破裂準則，分別為巖體細觀顆粒二維平行粘結拉伸強度、抗剪強度，分別為第i個接觸的含指數型時間效應且考慮彎矩貢獻因子的巖體細觀顆粒二維平行粘結正應力、剪應力，

第i個接觸的含指數型時間效應且考慮彎矩貢獻因子的巖體細觀顆粒二維平行粘結正應力的計算公式為第i個接觸的含指數型時間效應的巖體細觀顆粒二維平行粘結剪應力的計算公式為

在該準則的二維平行粘結應力中包含了指數型時間效應，見巖體細觀顆粒二維平行粘結直徑的指數型時效衰減因子計算公式β₁、β₂分別為控制巖體細觀顆粒平行粘結時效劣化的第一控制參數、第二控制參數；

f^s大于等于0表示巖體細觀顆粒二維平行粘結剪切破裂，小于0表示巖體細觀顆粒二維平行粘結未發生剪切破裂；fⁿ大于等于0表示巖體細觀顆粒二維平行粘結拉伸破裂，小于0表示巖體細觀顆粒二維平行粘結未發生拉伸破裂。

巖體時效破裂后考慮阻尼效應的二維線性接觸模型是指巖體細觀顆粒平行粘結時效破裂后，通過給定的二維線性接觸參考距離g_r設置了細觀顆粒二維線性接觸距離g_s，見巖體細觀顆粒二維線性接觸距計算公式其中，為巖體內部顆粒與顆粒二維線性接觸端a的坐標，為巖體內部顆粒與顆粒二維線性接觸端b的坐標，R^a、R^b分別為巖體細觀二維線性接觸端a的顆粒半徑和二維線性接觸端b的顆粒半徑；設置考慮巖體細觀顆粒間受力變形的二維線性接觸模式，在巖體顆粒之間設置考慮二維滑動摩擦線力的作用模式，巖體細觀顆粒間受力變形的二維線性接觸法向線性力計算公式取M_l＝1為相對矢量累加模式，取M_l＝0為絕對矢量累加模式，巖體細觀顆粒間受力變形的二維線性接觸切向線性力計算公式為其中，分別為巖體細觀顆粒間受力變形的二維線性接觸法向線性力、切向線性力，k_n、k_s分別為巖體細觀顆粒間受力變形的二維線性接觸法向、切向線性剛度，Δδ_n、Δδ_s分別為法向位移增量、切向位移增量，分別為初始法向力增量值和切向力增量值，為顆粒未滑動時的靜摩擦力，為巖體細觀顆粒滑動摩擦力，通過摩擦系數μ與乘積得到；同時設置二維線性接觸的阻尼模式，其中法向阻尼采用全法向模式M_d＝{0,2}和無拉伸模式M_d＝{1,3}兩種，通過公式計算，其中m_c為等效顆粒質量，按公式計算，切向阻尼采用全剪切模式M_d＝{0,1}和滑-剪模式M_d＝{2,3}，按照公式來計算，其中：分別為法向阻尼力、切向阻尼力，β_n為法向阻尼系數、β_s為切向阻尼系數，為法向速率、切向速率，F^*為巖體細觀顆粒線性接觸的全法向阻尼力，表達式為m_c為等效顆粒質量，m⁽¹⁾為二維線性接觸端1的巖體細觀顆粒質量，m⁽²⁾為二維線性接觸端2的巖體細觀顆粒質量。

本發明考慮彎矩貢獻因子的二維時效破裂模型的構建方法，包括如下步驟：

步驟1：設定巖體細觀顆粒平行粘結接觸的幾何參數量包括平行粘結面積和平行粘結慣性矩，R^a、R^b分別為二維平行粘結接觸a端的顆粒半徑、b端的顆粒半徑，為巖體細觀顆粒平行粘結直徑或半徑乘數，在二維情況下，平行粘結單位厚度為1時的平行粘結面積A和平行粘結慣性矩I分別通過公式(2)、公式(3)來確定：

其中：為巖體細觀顆粒二維平行粘結半徑，為巖體細觀顆粒二維平行粘結直徑乘數，A為巖體細觀顆粒二維平行粘結面積，I為巖體細觀顆粒二維平行粘結慣性矩；

步驟201：利用巖體細觀顆粒二維平行粘結時效衰減劣化的初始時間步長增量Δt，通過指數型函數計算巖體細觀顆粒二維平行粘結時效衰減劣化的直徑，公式(4)來確定：

其中：為考慮彎矩貢獻因子的二維平行粘結法向應力，為判斷巖體細觀顆粒二維平行粘結開始時效劣化衰減時的應力閥值，為巖體細觀顆粒二維平行粘結的拉伸強度，為考慮彎矩貢獻因子的二維平行粘結應力比，β₁、β₂分別為巖體細觀顆粒平行粘結時效劣化的第一控制參數、第二控制參數，為巖體細觀顆粒二維平行粘結隨時間劣化衰減的直徑，為巖體細觀顆粒二維平行粘結未衰減時的直徑，e為自然常數，Δt為巖體細觀顆粒二維平行粘結時效衰減劣化的時間增量；

步驟202：根據步驟201中的公式(4)，設定巖體細觀顆粒二維平行粒粘結直徑的指數型時效衰減因子β，見公式(5)：

其中：A'、I'、分別表示為巖體細觀顆粒二維平行粘結隨時間劣化衰減的平行粘結直徑、平行粘結半徑、平行粘結面積、平行粘結慣性矩、平行粘結直徑乘數，A、I、為巖體細觀顆粒平行粘結未衰減時的平行粘結直徑、平行粘結半徑、平行粘結面積、平行粘結慣性矩、平行粘結直徑乘數；

步驟203：根據步驟1中的公式(1)～公式(3)以及步驟202中的公式(5)，設定巖體細觀顆粒二維平行粘結幾何參數時效劣化衰減模式；巖體細觀顆粒二維平行粘結直徑隨著時間增加而不斷劣化衰減，二維平行粘結單位厚度為1時的平行粘結面積和平行粘結慣性矩也隨著時間增加而不斷劣化衰減，分別見公式(6)、公式(7)：

其中：A'、I'分別表示為巖體細觀顆粒二維平行粘結隨時間劣化衰減的平行粘結半徑、平行粘結面積、平行粘結慣性矩，A、I為巖體細觀顆粒二維平行粘結未衰減時的平行粘結面積、平行粘結慣性矩；

步驟204：依次計算第j個至第k個的巖體細觀顆粒包含時間效應的二維平行粘結法向彎矩增量；在二維情況下，由平行粘結兩端顆粒的速度、角速度和給定的循環計算時間步長增量Δt_c，通過公式(8)、公式(9)、公式(10)確定第i個巖體細觀顆粒二維平行粘結相對轉角二維平行粘結法向增量位移以及二維平行粘結切向增量位移再結合步驟203中的公式(7)和步驟202中的公式(5)，確定第i個巖體細觀顆粒包含時間效應的二維平行粘結彎矩增量，具體見公式(11)：

其中，ff、j、k是自然數，且2≤j≤ff≤k，j為每次循環計算中，包含時間效應的巖體細觀顆粒二維平行粘結衰減后未破裂的初始標號值，ff為中間某一個標號值，k為每次循環計算中，包含時間效應的巖體細觀顆粒二維平行粘結衰減后未破裂的最末標號值，i為第一個至最后一個平行粘結顆粒標號值，分別為第i個巖體細觀顆粒二維平行粘結接觸的a端和b端的絕對運動速度和角速度，n_n和n_s為巖體細觀顆粒二維平行粘結接觸面的法向單位向量和切向單位向量，和分別為巖體細觀顆粒二維平行粘結法向位移增量和切向位移增量，為巖體細觀顆粒二維平行粘結法向剛度，為巖體細觀顆粒二維平行粘結彎矩增量。

巖體細觀顆粒二維平行粘結時效衰減劣化的初始時間步長增量Δt的確定，是采用考慮彎矩貢獻因子的平行粘結時效劣化衰減的二維指數型模式，由每個時間步內的二維平行粘結首次衰減破裂所損耗的時間來確定，也即通過第一個平行粘結按指數型模式進行衰減破裂所歷時的時間除以直至第一個平行粘結破裂所需要的計算循環次數來估算初始時間步長增量Δt，見公式其中，為第i個接觸的巖體細觀顆粒二維平行粘結直徑乘數，n_c為第一個巖體細觀顆粒二維平行粘結破裂所需的循環計算的次數，β_σ、β_τ分別為巖體細觀顆粒二維平行粘結拉伸強度對應的時效劣化因子、二維平行粘結剪切強度對應的時效劣化因子，i依次為第一個至最后一個巖體細觀顆粒平行粘結數，∞為無窮大。

巖體細觀顆粒二維平行粘結拉伸強度對應的時效劣化因子β_σ和巖體細觀顆粒二維平行粘結剪切強度對應的時效劣化因子β_τ的確定包括如下步驟，其中，這些步驟中包含的公式下標1代表第一個按指數型模式進行時效衰減劣化的二維平行粘結破裂標號：

步驟211：在二維情況下，由巖體細觀顆粒平行粘結兩端顆粒的速度、角速度和給定的循環計算時間步長增量Δt_c，通過公式確定平行粘結接觸的相對轉角通過公式確定平行粘結法向增量位移通過公式確定平行粘結切向增量位移通過公式確定平行粘結接觸的彎矩增量；

步驟212：根據步驟211中的公式通過公式確定平行粘結法向力；根據步驟211中的公式通過公式確定平行粘結切向力；根據步驟211中的公式和公式通過公式確定平行粘結切向彎矩；通過公式確定平行粘結法向彎矩，其中，+＝為加法自反運算符，-＝為減法自反運算符；

步驟213：在二維情況下，通過公式確定平行粘結正應力，通過公式確定平行粘結剪應力，將這兩個公式中A、I以及用A'、I'及替換，然后將步驟203中的公式(6)和公式(7)以及步驟202中的公式(5)代入，獲得包含指數型時間效應和彎矩貢獻因子的二維平行粘結正應力計算公式和包含指數型時間效應的二維平行粘結剪應力計算公式

步驟214：將代入公式并令β＝β_σ，將代入公式并令β＝β_τ，據此，分別得到所述巖體細觀顆粒二維平行粘結拉伸強度對應的時效劣化因子以及巖體細觀顆粒二維平行粘結剪切強度對應的時效劣化因子

步驟205：根據步驟203中的公式(6)和公式(7)、步驟204中的公式(8)、公式(9)和公式(11)以及步驟202中的公式(5)，依次更新計算第j個至第k個巖體細觀顆粒平行粘結未破裂并包含時間效應的二維平行粘結法向力、切向力和切向彎矩；通過公式(12)、公式(13)、公式(14)計算第i個巖體細觀顆粒二維平行粘結接觸的平行粘結法向力、切向力和切向彎矩；在二維情況下，通過公式(15)來確定巖體細觀顆粒平行粘結法向彎矩：

法向力：

切向力：

切向彎矩：

法向彎矩：

其中：分別為第i個巖體細觀顆粒包含時間效應的平行粘結法向力、平行粘結切向力、包含時間效應的平行粘結法向彎矩、平行粘結切向彎矩、平行粘結法向位移增量和平行粘結切向位移增量，為巖體細觀顆粒二維平行粘結切向剛度，+＝為加法自反運算符，-＝為減法自反運算符。

步驟206：設置彎矩貢獻因子考慮彎矩對巖體細觀顆粒平行粘結法向正應力的貢獻程度，根據二維平行粘結正應力計算公式和二維平行粘結剪應力計算公式同時將這兩個公式中A、I以及用A'、I'及替換，然后將步驟203中的公式(6)和公式(7)以及步驟202中的公式(5)代入，獲得包含指數型時間效應和彎矩貢獻因子的二維平行粘結正應力和二維平行粘結剪應力計算公式，分別見公式(16)和公式(17)。

步驟207：將步驟206中包含時間效應的代入公式(18)，可確定考慮彎矩貢獻因子且帶拉伸截止限的摩爾-庫倫時效破裂準則，并且依次計算第j個至第k個的二維平行粘結應力，用于判斷巖體細觀顆粒平行粘結是否破裂以及破裂模式；在該準則的巖體細觀顆粒平行粘結應力中包含了指數型時間效應和考慮彎矩貢獻因子。

其中：f^s、fⁿ分別為巖體細觀顆粒二維平行粘結的時效剪切破裂準則、時效拉伸破裂準則，為第i個接觸的含指數型時間效應的二維平行粘結剪應力，為第i個接觸的含指數型時間效應且考慮彎矩貢獻因子的二維平行粘結正應力，分別為巖體細觀顆粒二維平行粘結的拉伸強度、抗剪強度，為巖體細觀顆粒二維平行粘結的粘聚力，為巖體細觀顆粒二維平行粘結的內摩擦角；f^s大于等于0表示巖體細觀顆粒平行粘結剪切破裂，小于0表示巖體細觀顆粒平行粘結未發生剪切破裂；fⁿ大于等于0表示巖體細觀顆粒平行粘結拉伸破裂，小于0表示巖體細觀顆粒平行粘結未發生拉伸破裂；

步驟208：如果步驟207中的公式(18)中的f^s或fⁿ大于等于0，表明巖體細觀顆粒的平行粘結發生了破裂，此后巖體細觀顆粒的運動模式采用考慮阻尼效應的二維線性接觸模型來表達；如果步驟207中的公式(18)中的f^s和fⁿ都小于0，表明平行粘結未破裂，繼續循環步驟201至207，計算、更新、判斷巖體細觀顆粒接觸的平行粘結狀態，直至巖體不產生新的平行粘結破裂或者平行粘結破裂加速發展而形成宏觀破壞，循環終止。

巖體細觀顆粒平行粘結發生破裂后，巖體細觀顆粒的運動模式采用考慮阻尼效應的二維線性接觸模型來表達，用于描述巖體細觀顆粒平行粘結時效破裂后細觀顆粒的應力、變形及運行規律，考慮阻尼效應的二維線性接觸模型的構建包括如下步驟：

步驟301：通過Monte Carlo搜索算法，遍歷尋找巖體細觀顆粒每個二維線性接觸端a、二維線性接觸端b(顆粒與顆粒、顆粒與墻)的中心坐標，在二維情況下，通過公式(19)計算兩者中心距離：

其中：d為二維線性接觸兩端顆粒與顆粒或者顆粒與墻之間的中心距離，為二維線性接觸端a的坐標，為二維線性接觸端b的坐標。

步驟302：二維平面狀態下巖體細觀顆粒間每個接觸點的單位向量通過公式(20)計算，如果是顆粒與顆粒之間的接觸，利用步驟301中得到二維線性接觸兩端的中心點坐標及距離計算，如果是顆粒與墻接觸，直接利用墻體的法向量等效替換來計算，確定每個接觸端的單位向量：

其中：n_i為接觸的單位矢量，為接觸端b的方向向量，為接觸端a的方向向量，n_wall為約束墻的方向向量。

步驟303：巖體細觀顆粒平行粘結破裂后，二維線性接觸段的接觸重疊量U，通過步驟301計算顆粒間距d以及二維線性接觸兩端的顆粒半徑R^a、R^b，再利用公式(21)來確定。通過設定顆粒二維線性接觸參考距離g_r，并結合公式(22)，確定顆粒二維線性接觸的距離g_s：

g_s＝|U|-g_r (22)

步驟304：確定巖體細觀顆粒接觸點法向、切向等效剛度，利用接觸兩端顆粒實體或是墻體的剛度k^a，k^b等效代替為接觸點的剛度(法向剛度和切向剛度的統稱)，按公式(23)計算：

其中：K_n、K_s為巖體細觀顆粒接觸點等效的法向剛度和切向剛度，為顆粒與顆粒或者顆粒與墻的接觸a端的法向剛度和切向剛度，為顆粒與顆粒或者顆粒與墻的接觸b端的法向剛度和切向剛度。

步驟305：確定巖體中接觸兩端顆粒間的相對運動速度，利用公式(24)、公式(25)來計算。其中e_pqz為Ricci指標置換符號，按照公式(26)來計算：

其中：V_p與V_q等價，V_p與V_q為巖體中接觸兩端顆粒間的相對運動速度，p、q為指標等價符號，p＝1，q＝1表示顆粒與顆粒接觸，p＝2，q＝2時表示顆粒與墻接觸，為顆粒與顆粒或是顆粒與墻的接觸b端單元的速度，為顆粒與顆粒或是顆粒與墻的接觸a端單元的速度，為顆粒與顆粒或是顆粒與墻的接觸a端單元的角速度，為顆粒與顆粒或是顆粒與墻的接觸b端單元的角速度，為顆粒與顆粒或是顆粒與墻的接觸a端的位移，為顆粒與顆粒或是顆粒與墻的接觸b端的位移，為位移指標變換的中間過渡符號，表示指標符號為p時顆粒-顆粒或者顆粒-墻的接觸a端的速度，表示指標符號為q時顆粒-顆粒或者顆粒-墻的接觸a端的速度，表示指標符號為p時顆粒-顆粒或者顆粒-墻的接觸b端的速度，表示指標符號為q時顆粒-顆粒或者顆粒-墻的接觸b端的速度(只有a端和b端兩個接觸端)。

步驟306：對于巖體細觀顆粒線性接觸模型的初始時間步長增量Δt的取值，通過公式(29)估計最小的時間步長Δt，確保所構建模型的計算時間步長小于該值，即可保證系統積分計算趨于穩定；通過公式(30)、公式(31)、公式(32)確定每個線性接觸的總位移增量、法向位移增量和切向位移增量：

R＝min(R_a,R_b) (27)

ΔU_p1＝V_p1Δt (30)

其中：R為巖體細觀顆粒的等效半徑，m為巖體細觀顆粒質量，J1為巖體細觀顆粒的轉動慣量；k^平為巖體細觀顆粒系統平移剛度，k^轉為巖體細觀顆粒系統旋轉剛度；ΔU_p1為巖體細觀顆粒二維線性接觸的總位移增量，Δδ_n、物理意義相同，均表示巖體細觀顆粒二維線性接觸的法向位移增量，Δδ_s、物理意義相同，均表示巖體細觀顆粒二維線性接觸的切向位移增量，V_p1與V_q1為巖體細觀顆粒接觸兩端的相對運動速度，n為單位法向量，p1,q1為張量指標變換符號。

步驟307：由公式(22)判定巖體細觀顆粒表面接觸允許存在的最大距離，計算法向和切向位移更新因子，另外，巖體細觀顆粒二維線性接觸法向位移增量的更新是采用前一步的法向位移增量與更新因子α的乘積獲得，巖體細觀顆粒二維線性接觸切向位移增量的更新是采用前一步的切向位移增量與更新因子α的乘積獲得。

其中：(g_s)₀為模型計算初始時刻的表面接觸距離，g_s為巖體細觀顆粒接觸的距離，α為位移更新因子。

步驟308：巖體細觀顆粒二維線性接觸的法向線性力采取相對矢量累加(M_l＝1)和絕對矢量累加(M_l＝0)模式，通過公式(33)、(34)計算獲得；巖體細觀顆粒二維線性接觸的切向線性力采用巖體細觀顆粒接觸滑動來表示，通過公式(35)計算獲得：

其中：分別為巖體細觀顆粒間受力變形的二維線性接觸法向線性力、切向線性力，k_n、k_s分別為巖體細觀顆粒間受力變形的二維線性接觸法向、切向線性剛度，Δδ_n、Δδ_s分別為巖體細觀顆粒二維線性接觸的法向位移增量、切向位移增量，分別為巖體細觀顆粒二維線性接觸的初始法向力增量值、切向力增量值，為巖體細觀顆粒未滑動時的靜摩擦力，為巖體細觀顆粒滑動摩擦力，其值可通過摩擦系數μ與乘積得到。

步驟309：巖體細觀顆粒線性接觸的法向阻尼采用全法向模式M_d＝{0,2}和無拉伸模式M_d＝{1,3}兩種，通過公式(36)計算，其中m_c為等效顆粒質量，按公式(37)計算，巖體細觀顆粒線性接觸的切向阻尼采用全剪切模式M_d＝{0,1}和滑-剪模式M_d＝{2,3}，按照公式(38)來計算，

其中：分別為巖體細觀顆粒線性接觸的法向線性阻尼力、切向線性阻尼力，β_n為巖體細觀顆粒線性接觸的法向阻尼系數，β_s為巖體細觀顆粒線性接觸的切向阻尼系數，k_n為巖體細觀顆粒線性接觸的法向線性剛度，k_s為巖體細觀顆粒線性接觸的切向線性剛度，分別為巖體細觀顆粒線性接觸的法向速率和切向速率，F^*為巖體細觀顆粒線性接觸的全法向阻尼力，表達式為m_c為巖體細觀等效顆粒質量，m⁽¹⁾為巖體細觀顆粒接觸端1的細觀顆粒質量，m⁽²⁾為巖體細觀顆粒接觸端2的細觀顆粒質量，F^d為巖體細觀顆粒線性接觸的總阻尼力。

實驗實例

下面以深部巖體為實例，結合附圖詳述本發明模型的數值實現的具體過程，請參閱實例附圖說明中的圖13至圖15以及模型附圖說明中的圖1至圖11，來理解本發明模型的數值實現步驟及效果：

步驟1：采用C++編程語言，并結合fish語言，根據本發明的模型結構構建流程圖(圖12)，在數值平臺上實現了考慮彎矩貢獻因子的二維時效破裂模型。

步驟2：初步確定巖體時效破裂模型的細觀參數

粒徑比Rratio、線性接觸法向剛度kn(圖6)、線性接觸切向剛度ks(圖6)、顆粒密度ba_rho、顆粒接觸模量b_Ec、平行粘結法向剛度pb_kn(圖6)、平行粘結切向剛度pb_ks(圖6)、平行粘結模型pb_Ec、顆粒的摩擦系數ba_fric、平行粘結拉伸強度的平均值pb_sn_mean、平行粘結拉伸強度的標準差pb_sn_sdev、平行粘結粘聚力平均值pb_coh_mean、平行粘結粘聚力標準差pb_coh_sdev、平行粘結半徑乘數gamma(圖7)、平行粘結彎矩貢獻因子beta、法向阻尼系數Apfan(圖6)、切向阻尼系數Apfas(圖6)以及內摩擦角pb_phi(圖8)等19個參數，參數具體值見表一。

步驟3：生成巖體模型

根據高斯分布或weibull分布確定模型的平行粘結拉伸強度和粘聚力分布，通過均勻隨機函數分布法確定顆粒的粒徑分布；通過各向同性應力調整法及自適應動態膨脹法，調整顆粒的位置，減少顆粒重疊量；通過懸浮顆粒刪除法，刪除孤立顆粒，提高模型樣本的整體性，減少缺陷模型的生成。最后賦予模型材料平行粘結強度參數，生成具有真實巖體結構的巖體模型。巖體模型的直徑為50mm、高度為100mm(圖13)。

步驟4：精確標定本發明中模型的細觀物理力學參數

通過室內單軸和三軸壓縮試驗得到的應力-應變曲線，確定巖體的宏觀彈性模量峰值強度σ_p，以及泊松比通過優化方法，使巖體單、三軸壓縮模型的應力-應變曲線與室內試驗的應力-應變以及宏觀變形參數和強度參數吻合，獲得所構建模型的細觀物理力學參數。

步驟5：巖體時效力學參數標定

對巖體進行一系列不同應力強度比條件下的時效力學試驗，得到不同應力強度比條件下巖體變形隨時間演化的曲線(圖14)。通過參數擬合法，匹配實際巖體的時效變形過程，確定巖體細觀顆粒平行粘結時效劣化的第一控制參數β₁、第二控制參數β₂。

步驟6：巖體時效力學數值試驗

在荷載一定的條件下，分別設定不同的彎矩貢獻因子，獲得了彎矩貢獻因子對巖體時效變形和破壞的影響規律(圖15)。

表一：本發明模型的參數名稱及值

上述實施例中，公式的符號與圖1～圖11以及附圖說明中的符號相互對應。

其它未詳細說明的部分均為現有技術，以上所有參數均可通過查閱手冊或計算得到。本發明并不嚴格地局限于上述實施例。以上所述僅為本發明的特定實施例，并不用于限制本發明。凡在本發明的精神和原則之內所做的任何修改、等同替換及改進等，都在本發明的保護范圍之內。