本發明涉及電動汽車電池管理領域，具體涉及一種鋰電池soc在線估計方法。

背景技術：

近年來，隨著空氣質量的日益惡化以及石油資源的漸趨匱乏，新能源汽車，尤其是純電動汽車成為當今世界各大汽車公司的開發熱點。動力電池組作為電動汽車的關鍵部件，動力電池soc被用來直接反應電池的剩余電量，是整車控制系統制定最優能量管理策略的重要依據，動力電池soc值的準確估計對于提高電池安全可靠性、提高電池能量利用率、延長電池壽命具有重要意義。

目前，常用的soc估計方法主要有開路電壓法、安時積分法、卡爾曼濾波法和神經網絡法等。

鋰電池開路電壓(ocv)可以表現其當前狀態電池的放電能力，其與soc有良好的線性關系，根據ocv-soc關系估計soc的方法稱為開路電壓法。開路電壓在電池工作狀態下不能直接測量，只有在電池未工作的情況下才能近似測量，所以這種方法只適用于電動汽車的駐車狀態。通常，開路電壓法用于為其它估計方法提供soc的初始值。

安時積分方法的基本原理是電池在充放電過程中，通過電流對時間積分，可以計算出電池充入或放出的電量，將此電量除以電池當前狀態可用容量，再與電池初始soc進行相應的加減運算即可得出當前狀態soc值。安時積分法具有成本低、測量方便等優點，但在電動汽車場合應用時也有以下幾個問題：需要借助其它方法獲得soc初始值；電流測量精度對soc估計精度具有決定性影響；積分過程的累積誤差無法消除，一次計算過程中如果充放電時間過長，累積誤差可能導致估計結果不可靠。

神經網絡法具有良好的非線性映射能力，理論上動力電池的非線性特性能夠較好的由神經網絡映射，但其需要大量的數據進行訓練，使用復雜，訓練數據和訓練方法對估計精度的影響較大。

卡爾曼濾波法的核心思想是對動態系統的狀態做出最小均方意義上的最優估計，卡爾曼濾波的優點在于誤差糾正能力較強，不足在于估計精度對電池模型的準確性依賴較高。

因此需要建立一種簡單易行、估算精度較高，魯棒性強且能消除累積誤差的soc估計方法。

技術實現要素：

本發明的目的是針對上述現有技術的不足，提供了一種鋰電池soc在線估計方法，該方法采用基于最小二乘法和卡爾曼濾波法相結合的狀態變量的聯合估計算法，在一步遞推過程中先用最小二乘法更新卡爾曼濾波器的模型參數，再根據濾波得到的soc求出ocv，根據ocv和測得的電壓、電流信號用最小二乘法估計并更新下一步卡爾曼濾波運算中的模型參數，依次遞推。實現了比傳統無跡卡爾曼濾波算法精度更高，誤差收斂性更強的技術效果。

本發明的目的可以通過如下技術方案實現：

一種鋰電池soc在線估計方法，所述方法包括以下步驟：

1)在估算程序開始前，測量電池在靜止狀態下的開路電壓voc(0)，根據ocv-soc曲線，得到電池荷電狀態的初始值soc(0)；

2)根據電池的外特性建立電池的二階rc等效模型，該模型包括一個電壓源voc、一個直流內阻r以及兩個rc并聯環路，所述rc并聯環路包括rs、cs、rp和cp，根據電池工作初期的電壓響應曲線，通過曲線擬合的方法，估算電池等效模型的參數初始值r(0)、rs(0)、cs(0)、rp(0)和cp(0)；

3)啟動估算程序，根據步驟1)中電池荷電狀態的初始值soc(0)和步驟2)中電池等效模型的參數初始值r(0)、rs(0)、cs(0)、rp(0)和cp(0)，設定狀態方程的匹配系數初值；

4)利用自適應無跡卡爾曼濾波算法得到當前電池荷電狀態值soc(k)，根據ocv-soc曲線，得到當前的開路電壓voc(k)；

5)啟動帶遺忘因子的最小二乘法，對當前電池等效模型的參數r(k)、rs(k)、cs(k)、rp(k)和cp(k)進行辨識，將辨識出來的當前電池等效模型的參數更新狀態方程的匹配系數，求出下一時刻電池荷電狀態值；

6)重復步驟4)和步驟5)，反復推算，得到每個時刻的電池荷電狀態值。

優選的，所述步驟3)中設定狀態方程的匹配系數初值的具體過程為：根據電池的二階rc等效模型以及荷電狀態的積分法得：

其中，e(t)為電池開路電壓ocv值，u(t)為電池端電壓值，us為極化電容cs兩端的電壓，up為極化電容cp兩端的電壓，soc(t)為soc估計值，soc(t')為電池荷電狀態上一時刻的初始值，cn為電池最大可用容量，η為庫倫效率，對上式進行離散化，得狀態方程：

uk＝ek-ikr-us,k-up,k+υ(k)＝f(sock)-ikr-us,k-up,k+υ(k)

其中：

其中，as、bs、ap、bp為狀態方程的匹配系數，ω1(k)、ω3(k)、ω5(k)為系統噪聲。

優選的，所述步驟4)的具體過程為：

令：

為了便于區別，在此取xk＝[sock,us,k,up,k]為系統的原始狀態；取yk為原始輸出，對應電路模型中的uk；取uk為控制量，對應電路模型中的ik，且令ψ＝[y1,y2…yk]，然后進行自適應無跡卡爾曼濾波運算：

(1)狀態估計時間更新

基于上一時刻狀態最優估計得到擴展狀態的均值和方差，據此選擇(2l+1)個采樣點，最后將采樣點通過狀態方程進行變換并完成狀態預測：

一、初始化，初始狀態確定

二、狀態擴維

其中，q、r為協方差矩陣，是對稱的矩陣，對角線上是各個維度上的方差；

擴展狀態均值：

擴展狀態方差：

三、選取采樣點

sample＝{zi,xk-1,i}，其中i＝0、1、2、……2l+1，xk-1,i為所選粒子，zi是相應的加權值，粒子點按如下方式選取：

對應的加權系數為：

其中，λ為比例系數，滿足：λ＝α²(l+t)-l，z^(m)、z^(c)分別是粒子點均值和方差相對應的加權值；而表示(l+λ)px,k-1的平方根矩陣的第i列；參數t滿足t≥0以保證方差陣為正定，此處默認t＝0；α控制粒子分布距離，且滿足10^-2≤α≤1，在此取α＝1，β用于減小高階項誤差，對以正態分布最優取β＝2，分析采樣點又分為和三部分，據此進行狀態估計的時間更新為：

(2)均方誤差時間更新

(3)系統輸出先驗估計

(4)濾波增益矩陣計算

(5)狀態最優估計

(6)均方誤差估計

由于過程噪聲和測量噪聲都是時變的，為了讓噪聲協方差實時更新，令：

其中，μk和yk|k-1,i分別是測量輸出量的殘差和各sigma點估算得到的測量輸出量的殘差，即可實現過程噪聲和測量噪聲的實時更新。

優選的，所述步驟5)的具體過程為：

將狀態方程進行拉普拉斯變化得

所以：

其中，g(s)為回路阻抗的拉普拉斯形式；

采用雙線性變換進行離散化，令可得離散化的傳遞函數：

其中，a1、a2、a3、a4、a5為相應的常數系數，將上式轉化成差分方程可得：

y(k)＝e(k)-u(k)

＝a1y(k-1)+a2y(k-2)+a3i(k)+a4i(k-1)+a5i(k-2)

其中，i(k)為系統輸入，y(k)為系統輸出，令：

θ＝[a1a2a3a4a5]^t

設k時刻傳感器采樣誤差為e(k)，則：

將擴展為n維，k＝1,2,……n+n,n＝2，可得如下式子：

y＝[y(3),y(4),y(5)……y(n+2)]^t

e＝[e(3),e(4),e(5)……e(n+2)]^t

取泛函數j(θ)：

因為最小二乘法原理是使j(θ)取最小值，所以求j(θ)極值，令：

可得：

對上述過程通過遞推最小二乘法進行遞推運算，如下所示：

其中，是上一時刻系統所估計的參考值，是此時刻的觀測值，y(k+1)作為系統實際的觀測值，與相減后便為預測誤差，將預測誤差與增益項k(k+1)相乘，便是此刻預測值的校正，最終獲得此時刻最優估計值必須提供符合條件的和p(0)，才能獲得增益項k(k+1)，進而啟動最小二乘法，為任意值，p(0)＝αi，α為單位陣的系數，i為單位陣；

遞推最小二乘法是具有無限記憶長度的算法，對于電池系統，最小二乘法在遞推運算過程中舊數據越來越多會導致遞推結果不能良好的反應新數據的特性，為避免上述情況，引入遺忘因子λ，0<λ<1，即：

所以，即使(n+1)很大，p(n+1)也不趨于0，有效的克服了“數據飽和”現象，所述帶遺忘因子最小二乘算法的步驟為：

當λ＝1時，為普通最小二乘法，λ越小跟蹤能力越強，但波動也越大；

由上述節算法求出θ值后，令：

可得：

由系數對應相等可得：

此式右邊的系數通過遞推算法求出，左邊即是模型的未知參數，至此帶有遺忘因子的最小二乘法參數辨識的推導過程完成。

優選的，所述遺忘因子λ的取值范圍為：0.95<λ<1。

本發明與現有技術相比，具有如下優點和有益效果：

1、本發明通過使用帶遺忘因子的最小二乘法與自適應無跡卡爾曼濾波濾波算法相結合，估計動力電池荷電狀態值，實現了比傳統無跡卡爾曼濾波算法精度更高，誤差收斂性更強的技術效果。

2、本發明通過采用遺忘因子λ(0<λ<1)，避免了最小二乘法遞推過程中舊數據越來越多、導致遞推結果不能良好的反應新數據的特性的問題，有效的克服了“數據飽和”現象。

3、本發明在自適應無跡卡爾曼濾波算法(aukf)中，將每次測量的輸出值和模型估計到的輸出值的殘差及各狀態sigma點估算的輸出值殘差的加權作為新息來估計當前時刻的噪聲協方差，讓協方差隨時間而更新，改變了傳統無跡卡爾曼濾波算法(ukf)中協方差為常量不能滿足噪聲實時更新的特性，從而提高了估計精度。

附圖說明

圖1為本發明實施例估計方法的流程圖。

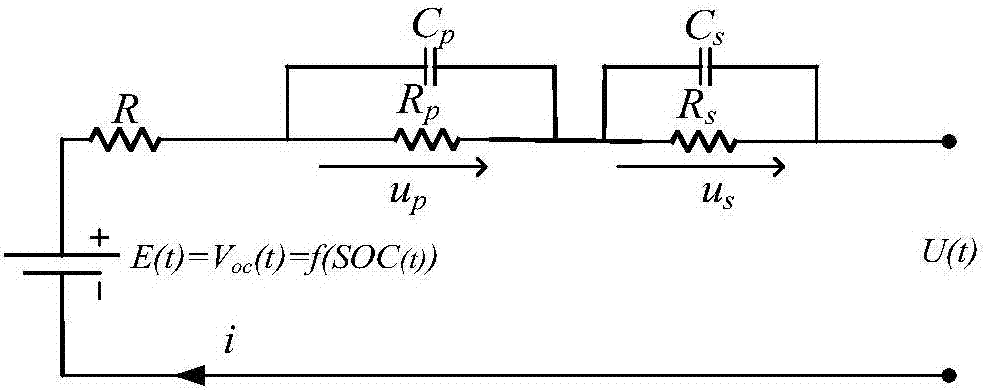
圖2為本發明實施例根據電池的外特性建立的電池二階rc等效模型。

圖3為鋰電池放電結束端的電壓響應曲線。

圖4為本發明所述鋰電池soc在線聯合估計算法與傳統自適應無跡卡爾曼濾波算法的soc估計值比較圖。

圖5為本發明所述鋰電池soc在線聯合估計算法與傳統自適應無跡卡爾曼濾波算法的soc估計值誤差比較圖。

具體實施方式

下面結合實施例及附圖對本發明作進一步詳細的描述，但本發明的實施方式不限于此。

實施例：

本實施例提供了一種鋰電池soc在線估計方法，如圖1所示，所述方法包括以下步驟：

步驟一、在估算程序開始前，測量電池在靜止狀態下的開路電壓voc(0)，根據ocv-soc曲線，得到電池荷電狀態的初始值soc(0)；

步驟二、根據電池放電結束端的電壓響應曲線，如圖3所示，建立電池的二階rc等效模型，如圖2所示，該模型包括一個電壓源voc、一個直流內阻r以及兩個rc并聯環路，所述rc并聯環路包括rs、cs、rp和cp，根據電池工作初期的電壓響應曲線，通過曲線擬合的方法，估算電池等效模型的參數初始值r(0)、rs(0)、cs(0)、rp(0)和cp(0)；

步驟三、啟動估算程序，根據步驟一中電池荷電狀態的初始值soc(0)和步驟二中電池等效模型的參數初始值r(0)、rs(0)、cs(0)、rp(0)和cp(0)，設定狀態方程的匹配系數初值；

其中，步驟3)中設定狀態方程的匹配系數初值的具體過程為：根據電池的二階rc等效模型以及荷電狀態的積分法得：

其中，e(t)為電池開路電壓ocv值，u(t)為電池端電壓值，us為極化電容cs兩端的電壓，up為極化電容cp兩端的電壓，soc(t)為soc估計值，soc(t')為電池荷電狀態上一時刻的初始值，cn為電池最大可用容量，η為庫倫效率，對上式進行離散化，得狀態方程：

uk＝ek-ikr-us,k-up,k+υ(k)＝f(sock)-ikr-us,k-up,k+υ(k)

其中：

其中，as、bs、ap、bp為狀態方程的匹配系數，ω1(k)、ω3(k)、ω5(k)為系統噪聲。

步驟四、利用自適應無跡卡爾曼濾波算法得到當前電池荷電狀態值soc(k)，根據ocv-soc曲線，得到當前的開路電壓voc(k)；

其中，所述步驟4)的具體過程為：

令：

為了便于區別，在此取xk＝[sock,us,k,up,k]為系統的原始狀態；取yk為原始輸出，對應電路模型中的uk；取uk為控制量，對應電路模型中的ik，且令ψ＝[y1,y2…yk]，然后進行自適應無跡卡爾曼濾波運算：

(1)狀態估計時間更新

基于上一時刻狀態最優估計得到擴展狀態的均值和方差，據此選擇(2l+1)個采樣點，最后將采樣點通過狀態方程進行變換并完成狀態預測：

一、初始化，初始狀態確定

二、狀態擴維

其中，q、r為協方差矩陣，是對稱的矩陣，對角線上是各個維度上的方差；

擴展狀態均值：

擴展狀態方差：

三、選取采樣點

sample＝{zi,xk-1,i}，其中i＝0、1、2、……2l+1，xk-1,i為所選粒子，zi是相應的加權值，粒子點按如下方式選取：

對應的加權系數為：

其中，λ為比例系數，滿足：λ＝α²(l+t)-l，z^(m)、z^(c)分別是粒子點均值和方差相對應的加權值；而表示(l+λ)px,k-1的平方根矩陣的第i列；參數t滿足t≥0以保證方差陣為正定，此處默認t＝0；α控制粒子分布距離，且滿足10^-2≤α≤1，在此取α＝1，β用于減小高階項誤差，對以正態分布最優取β＝2，分析采樣點又分為和三部分，據此進行狀態估計的時間更新為：

(2)均方誤差時間更新

(3)系統輸出先驗估計

(4)濾波增益矩陣計算

(5)狀態最優估計

(6)均方誤差估計

由于過程噪聲和測量噪聲都是時變的，為了讓噪聲協方差實時更新，令：

其中，μk和yk|k-1,i分別是測量輸出量的殘差和各sigma點估算得到的測量輸出量的殘差，即可實現過程噪聲和測量噪聲的實時更新。

步驟五、啟動帶遺忘因子的最小二乘法，對當前電池等效模型的參數r(k)、rs(k)、cs(k)、rp(k)和cp(k)進行辨識，將辨識出來的當前電池等效模型的參數更新狀態方程的匹配系數，求出下一時刻電池荷電狀態值；

其中，所述步驟5)的具體過程為：

將狀態方程進行拉普拉斯變化得

所以：

其中，g(s)為回路阻抗的拉普拉斯形式；

采用雙線性變換進行離散化，令可得離散化的傳遞函數：

其中，a1、a2、a3、a4、a5為相應的常數系數，將上式轉化成差分方程可得：

y(k)＝e(k)-u(k)

＝a1y(k-1)+a2y(k-2)+a3i(k)+a4i(k-1)+a5i(k-2)

其中，i(k)為系統輸入，y(k)為系統輸出，令：

θ＝[a1a2a3a4a5]^t

設k時刻傳感器采樣誤差為e(k)，則：

將擴展為n維，k＝1,2,……n+n,n＝2，可得如下式子：

y＝[y(3),y(4),y(5)……y(n+2)]^t

e＝[e(3),e(4),e(5)……e(n+2)]^t

取泛函數j(θ)：

因為最小二乘法原理是使j(θ)取最小值，所以求j(θ)極值，令：

可得：

對上述過程通過遞推最小二乘法進行遞推運算，如下所示：

其中，是上一時刻系統所估計的參考值，是此時刻的觀測值，y(k+1)作為系統實際的觀測值，與相減后便為預測誤差，將預測誤差與增益項k(k+1)相乘，便是此刻預測值的校正，最終獲得此時刻最優估計值必須提供符合條件的和p(0)，才能獲得增益項k(k+1)，進而啟動最小二乘法，為任意值，p(0)＝αi，α為單位陣的系數，i為單位陣；

遞推最小二乘法是具有無限記憶長度的算法，對于電池系統，最小二乘法在遞推運算過程中舊數據越來越多會導致遞推結果不能良好的反應新數據的特性，為避免上述情況，引入遺忘因子λ，0<λ<1，即：

所以，即使(n+1)很大，p(n+1)也不趨于0，有效的克服了“數據飽和”現象，所述帶遺忘因子最小二乘算法的步驟為：

當λ＝1時，為普通最小二乘法，λ越小跟蹤能力越強，但波動也越大，這里遺忘因子λ的取值范圍為：0.95<λ<1；

由上述節算法求出θ值后，令：

可得：

由系數對應相等可得：

此式右邊的系數通過遞推算法求出，左邊即是模型的未知參數，至此帶有遺忘因子的最小二乘法參數辨識的推導過程完成。

步驟六、重復步驟四和步驟五，反復推算，得到每個時刻的電池荷電狀態值。

由圖4與圖5所示的本發明所述鋰電池soc在線聯合估計算法與傳統自適應無跡卡爾曼濾波算法的soc估計值比較圖與soc估計值誤差比較圖可以看出，本發明所述聯合估計算法相比于傳統無跡卡爾曼濾波算法精度更高、誤差收斂性更強。

以上所述，僅為本發明專利較佳的實施例，但本發明專利的保護范圍并不局限于此，任何熟悉本技術領域的技術人員在本發明專利所公開的范圍內，根據本發明專利的技術方案及其發明專利構思加以等同替換或改變，都屬于本發明專利的保護范圍。