本發明屬于電池能源管理系統領域，涉及到電池能量管理系統以及鋰電池荷電狀態估計以及鋰電池電池模型參數辨識。

背景技術：

鋰電池以其高能量密度和高比功率廣泛應用在電動汽車電池系統中，電池的性能決定著電動汽車系統的安全性、可靠性以及效率。電池管理系統(BMS)需要提供精確的電池狀態信息以供參考。電池荷電狀態(SOC)是電池管理系統的核心，只有精確的鋰電池SOC預測才可以準確預測電池的剩余電量，同時確定有效的電池管理策略，從而避免電池的過充電和過放電損壞電池，延長電池的使用壽命。

然而SOC不能夠直接測量到，必須通過可測量的電壓、電流和溫度等的參數來預測，SOC預測的準確性對電池的使用效率、使用壽命以及安全性有著決定性影響。

技術實現要素：

本發明的目的是提供一種高精度、快收斂速度以及低計算復雜度的鋰電池SOC預測方法。采用本發明的預測方法，能夠在實時運行環境下提高鋰電池的估計精度，提高電池管理系統的安全性和可靠性。技術方案如下：

一種鋰電池SOC預測方法，包括下列步驟：

(1)建立鋰電池混合電化學模型，電池模型的狀態方程為：

觀測方程為：

式中，SOC(t)為t時刻的瞬時SOC預測值，SOC(0)為初始SOC值，i(t)為t時刻的瞬時電流，η為能量轉換效率，Q_c為鋰電池電荷量，U(t)為t時刻端電壓值，K₀、K₁、K₂、K₃、K₄為鋰電池混合電化學模型待辨識參數，R₀為鋰電池歐姆內阻；

(2)對鋰電池進行充放電測試，獲取包括電池充放電電壓、電流以及溫度在內的實驗數據；

(3)采用遺忘因子最小二乘法進行辨識對鋰電池混合電化學模型中的參數進行在線辨識，得到鋰電池的電壓預測值；

(4)根據電壓預測均方根誤差值設置算法轉換閾值電壓U_th，聯合采用無跡卡爾曼濾波和粒子濾波算法，方法如下：計算實際電壓測量值和電壓預測值的差值Err(t)＝|Z(t)-U(t)|，其中：U(t)為t時刻電壓測量值，Z(t)為t時刻電壓預測值；判斷Err(t)是否大于算法轉換閾值電壓U_th，若Err(t)>U_th，則調用粒子濾波算法進行預測；否則，則調用無跡卡爾曼濾波算法進行預測。

本發明的有益效果如下：

1.本發明采用的混合算法結構能夠避免粒子濾波的高計算復雜度以及無跡卡爾曼濾波算法的低收斂速度，能夠同時擁有高精度、低計算復雜度以及快收斂速度。

2.電池模型利用遺忘因子最小二乘法進行在線辨識，模型的精度高，能夠充分體現鋰電池的動態特性。

附圖說明

圖1：DST測試電流波形。

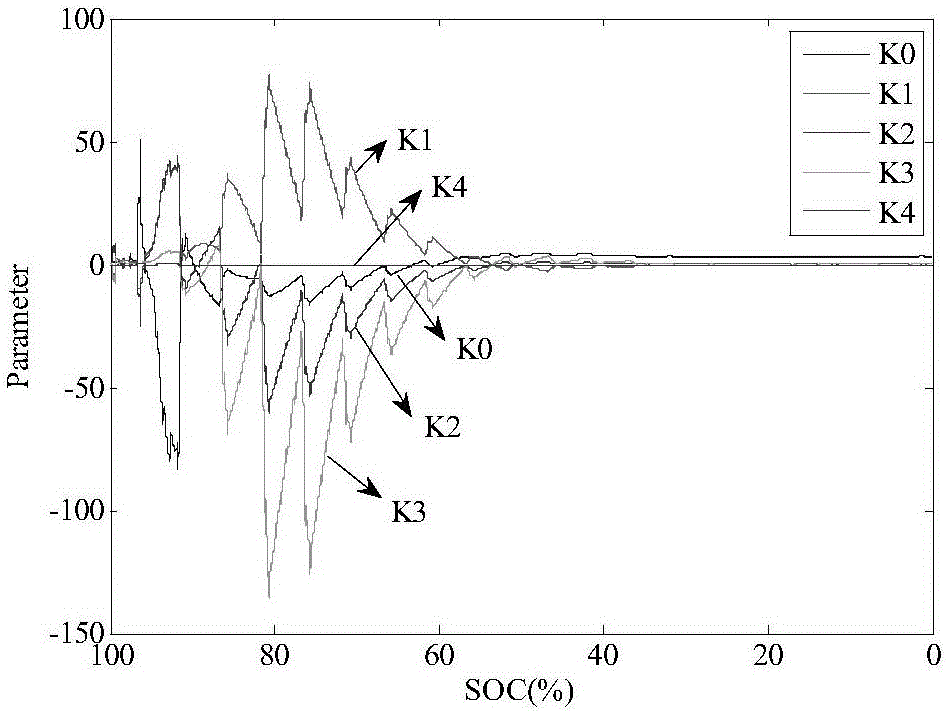
圖2：參數K0，K1，K2，K3和K4辨識結果。

圖3：參數R0辨識結果。

圖4：模型辨識電壓和測量電壓。

圖5：單個FUDS測試電流波形。

圖6：實驗過程中電流測試波形。

圖7：實驗過程中電壓測量值。

圖8：實驗過程中SOC值變化。

圖9：測量電壓和預測電壓對比。

圖10：電壓預測誤差。

圖11：初始值為100％時SOC預測效果對比圖。

圖12：初始值為100％時SOC預測誤差對比圖。

圖13：初始值為10％時SOC預測效果對比圖。

圖14：初始值為10％時SOC預測誤差圖。

具體實施方式

本發明在混合電化學模型的基礎上，提出使用遺忘因子最小二乘法(FFLS)對鋰電池電化學混合模型參數實現在線辨識，提高鋰電池模型精度。同時提出了一種鋰電池混合算法的預測模型，能夠實現鋰電池SOC預測的高精度以及快收斂速度，同時降低了運行過程中的計算復雜度。所采用的技術方案為：

1.算法模型依賴于電池模型，電池模型的精度嚴重影響著SOC預測精度，因此首先建立鋰電池混合電化學模型，電池模型的狀態方程為：

觀測方程為：

式中SOC(t)為t時刻的瞬時SOC預測值，SOC(0)為初始SOC值，i(t)為t時刻的瞬時電流，η為能量轉換效率，Q_c為鋰電池電荷量，U(t)為t時刻端電壓值，K₀、K₁、K₂、K₃、K₄為混合模型待辨識參數，R₀為鋰電池歐姆內阻。

2.采用USABC電池測試標準對電池進行充放電測試，獲取電池充放電電壓、電流以及溫度等實驗數據。

3.對電池模型中的參數進行在線辨識，采用遺忘因子最小二乘法進行辨識。遺忘因子最小二乘法的計算公式如下：

θ(t+1)＝θ(t)+K(t+1)[Z(t+1)-U(t+1)θ(t)]

K(t+1)＝P(t+1)U(t+1)[λ+U'(t+1)P(t)U(t+1)]^-1

式中θ(t)是第t次參數估計值，U(t+1)θ(t)是對本次觀測值的預測，Z(t+1)是t+1次實際觀測值，K(t+1)為增益項，P(t+1)為預測協方差矩陣。λ為遺忘因子，λ越小，算法跟蹤能力越強，波動越大。

4.利用Matlab軟件編寫混合鋰電池SOC預測算法，算法綜合了無跡卡爾曼濾波以及粒子濾波，以實際電壓測量值和電壓預測值的差值作為算法轉換判斷條件。

Err(t)＝|Z(t)-U(t)|

其中：U(t)為t時刻電壓測量值，Z(t)為t時刻電壓預測值。

判斷預測過程誤差Err(t)是否大于誤差閾值。若Err(t)>U_th，則調用粒子濾波算法部分進行預測；若Err(t)<U_th，則調用無跡卡爾曼濾波算法部分進行預測。

5.將混合算法的SOC預測結果、誤差、收斂時間以及運行時間和擴展卡爾曼濾波、無跡卡爾曼濾波、粒子濾波預測結果對比，驗證混合算法在精度和收斂速度以及計算復雜度方面具有明顯的優勢。

本實施采用德國Digatron動力電池測試系統，DSS1K8E可編程電子負載，以及USB2812數據采集卡，用于采集鋰電池端電壓、充放電電流以及溫度等數據。利用MATLAB軟件編寫遺忘因子最小二乘法程序在線辨識鋰電池參數，同時編寫混合算法程序，用其預測鋰電池SOC值。將預測結果與擴展卡爾曼、無跡卡爾曼以及粒子濾波預測結果對比，分析算法效果。具體實施步驟如下：

1.采用USABC電池測試標準中的DST測試電流對電池充放電，利用USB2812采集電池端電壓和電流以及溫度等數據，電流波形如圖1所示。

2.分析混合電化學模型，模型方程如下：

其中U(t)為t時刻模型端電壓，SOC(t)為t時刻SOC預測值，i(t)為t時刻電流。K₀，K₁，K₂，K₃，K₄以及R₀是待辨識參數。

3.利用MATLAB軟件編寫遺忘因子最小二乘法辨識算法，對混合電化學模型參數進行在線辨識。

模型方程可以改寫為：

E(t)＝C(t)X(t) (2)

式中：

X(t)＝[K₀,K₁,K₂,K₃,K₄,R₀]^T (4)

遺忘因子遞推最小二乘法的計算公式如式(5)～(7)所示：

θ(t+1)＝θ(t)+K(t+1)[Z(t+1)-U(t+1)θ(t)] (5)

K(t+1)＝P(t+1)U(t+1)[λ+U'(t+1)P(t)U(t+1)]^-1 (6)

式中θ(t)是第t次參數預測值，U(t+1)θ(t)是對本次觀測值的預測，Z(t+1)是t+1次實際觀測值，K(t+1)為增益項，P(t+1)為預測協方差矩陣。λ為遺忘因子，λ越小，算法跟蹤能力越強，波動越大。

K₀，K₁，K₂，K₃，K₄參數辨識結果如圖2所示，R₀參數辨識結果如圖3所示。模型辨識電壓及測量電壓如圖4所示，經計算模型電壓均方根誤差為0.0661V。

4.實驗采用FUDS測試條件對電池進行充放電控制，利用數據采集卡采集充放電過程電池端電壓和電流等數據。實驗過程中測量電壓如圖7所示，電流數據如圖6所示，SOC真實計算值如圖8所示。

5.利用MATLAB軟件編寫混合算法程序。

本方案所采用的混合算法流程如下：

(1)系統初始化。設置系統狀態噪聲方差矩陣Q，系統觀測噪聲方差矩陣R；初始化系統協方差矩陣P以及鋰電池電荷量Q_c；初始化狀態轉換電壓誤差閾值U_th；

(2)t＝1,2,3,···,N時刻，計算電壓誤差：

Err(t)＝|Z(t)-U(t)| (8)

其中：Z(t)為t時刻電壓測量值。

(3)t＝1,2,3,···,N時刻，判斷Err(t)是否大于誤差閾值U_th。若Err(t)>U_th，轉到(a)，若Err(t)<U_th，轉到(b)；

(a)粒子濾波算法。

(i)序列重要性采樣。從重要性密度函數中生成采樣粒子并根據公式(9)計算采樣粒子的權值。根據公式(10)對粒子的權值歸一化。

(ii)對采樣例子一步預測。

(iii)更新觀測預測并計算觀測誤差。

(iv)根據公式(9)更新粒子的權值，并進行歸一化。

(v)更新狀態預測和觀測預測。

(b)無跡卡爾曼濾波算法。

(i)Sigma粒子采樣及計算響應的權值。

λ＝α²(n+κ)-n (17)

其中，n是系統維數，是粒子均值，是第i個粒子的權值，是第i個粒子方差的權值，λ用來降低預測整體誤差，α為控制粒子分布變量，κ變量用來保證(n+λ)P矩陣半正定，β為非負權重系數。

(ii)根據狀態方程對采樣粒子一步預測。

狀態變量的均值以及方差計算如下：

(iii)根據觀測方程更新系統觀測預測。

采樣粒子觀測預測的均值以及方差計算如下：

(iv)計算系統協方差。

(v)計算卡爾曼增益。

K_t+1＝P_xzP_z^-1 (27)

(vi)更新系統狀態預測以及協方差。

P_t+1＝P_t-K_t+1P_tK_t+1^T (28)

(4)SOC狀態更新。

(5)根據測量電壓和測量電流更新鋰電池模型參數。

(6)更新模型電壓預測，轉到(2)。

6.確定合適的采樣粒子數目。粒子采樣數目影響粒子濾波的精度以及程序運行的時間(ADT)，確定合適的采樣粒子數目對于SOC預測十分重要，通過對比不同采樣粒子數目N_s，最終確定N_s選用100。不同N_s下粒子濾波算法精度和運行時間如表1所示。

表1：不同N_s下粒子濾波算法精度和運行時間

7.應用混合算法對鋰電池SOC進行預測，并對比擴展卡爾曼算法，無極卡爾曼算法以及粒子濾波算法與混合模型算法在精度、運行時間以及收斂速度。設置算法轉換閾值電壓U_th，為模型電壓預測均方根誤差0.0661V。初始值為100％時，SOC預測效果圖如圖11所示，誤差如圖12所示，平均絕對誤差(MAE)、均方根誤差(RMSE)以及運行時間如表2所示。

表2：預測誤差以及運行時間

SOC預測值到達MAE值時認為收斂到真實值。初始值為10％時，SOC預測效果如圖13所示，SOC預測誤差如圖14所示，收斂時間如表3所示。

表3：SOC預測收斂時間對比

實驗表明混合算法模型在精度、收斂速度以及計算復雜度方面具有明顯的優勢。