本發明涉及非平衡系統頻率估計技術領域，特別是涉及基于改進的smartdft算法的非平衡系統頻率估計方法。

背景技術：

在附加白高斯噪聲下，估計正弦信號或復指數信號的頻率、幅度、相位是非常重要的非線性問題，在電力系統分析、無線通信、雷達信號監測和語音分析中有著廣泛的應用。在不同的應用中，眾多文獻也提出了相對應的估計方法，如基于dft算法，最小二乘算法，自適應陷波器，卡爾曼濾波器和它的拓展，最大后驗概率算法和基于子空間投影的算法。

典型的，標準的n點dft操作在頻譜上可以得到2π/n的分辨率，但是在異步采樣下是不準確的。傳統方法上如果想要提高基于dft的頻率估計算法的精確度，額外的計算復雜度不可避免。在已有文獻中，提出過了一種smartdft(sdft)技術改善實時正弦信號頻率估計的準確度。也有文獻進一步應用了復值最小二乘框架改善了sdft的估計效果。基于窗口dft的插值算法可以獲得頻率估計的重要改善，因為信號序列的窗口可以減少頻譜泄漏和頻譜插值。dft算法的相角誤差可以估計相應模擬信號的真實頻率,由非相干dft采樣引起的泄漏效果也可以用于頻率估計。進一步，有文獻提出采用兩個階段去改善估計效果，第一階段實行n點dft的粗估計，接著在頻譜峰值附近進行第二階段的精確估計。

非圓信號廣泛應用于描述非平衡系統的動態狀態，例如非平衡三相電力系統、i-q不平衡通信系統等等。基于恰當的非圓信號統計分析，利用非平衡電壓的非圓統計特性，眾多文獻提出了一系列的估計模型，標準的頻率估計算法也可以進一步擴展為通用的形式。

無論是頻域的sdft技術還是時域的rphd技術還無法處理非平衡系統中的復值非圓信號，本專利意義在于基于復值非圓信號的特性，實現與以上技術的結合，完成在有噪條件下，對復值非圓信號頻率精確的估計和追蹤。

技術實現要素：

為了解決上述存在的問題，本發明提供基于改進的smartdft算法的非平衡系統頻率估計方法，擴展了原始的smartdft技術(sdft)，使此項技術不僅可以應用于實值正弦信號，也可以處理復值非圓信號。基于連續dft基頻分量間的線性預測(lp)性質，應用最小二乘框架可以減小模型的均方誤差，得到改進的復值最小二乘算法(cls)。同時，專利還提出了一種復值改進的pisarenko諧波分解算法(crphd),此方法可以移除噪聲的干擾獲得精確的頻率估計，可以有效應用在含有噪聲的非平衡三相電力系統中，為達此目的，本發明提供基于改進的smartdft算法的非平衡系統頻率估計方法，具體估計方法如下：

步驟1計算非圓信號第k點頻率分量：

沒有噪聲和諧波干擾的非平衡系統中的非圓信號可以表示為：參數α和β分別定義為這里a,b和是未知的確定性常量分別表示當前信號的幅度和相位，定義信號頻率這里k∈{1,2,…,n-1}，δ∈(0,1)分別是未知系統頻率的整數和小數部分，目標是根據n點dft變換后的第k頻點序列{xk(m)}找到ω0；

信號x(n)第k點dft頻率分量如下：

步驟2無噪條件下的sdft算法：

現在提出頻率估計算法：用定義參數的估計值；

定義公式(1)中的指數內核為；

如此，根據公式(1)和(2)，找到如下的關系：ak(m+1)＝rak(m)和bk(m+1)＝r^-1bk(m)，以及：

對公式(3)進行代數變換后，可以找到連續dft分量的線性預測關系：xk(m+1)+xk(m-1)＝μxk(m)，這里可以通過下式估計

因此，sdft算法可以通過計算來估計系統頻率這里表示取復數的實部；

步驟3有噪條件下cls優化處理：

現在考慮在噪聲環境下的非平衡系統：噪聲q(n)是均值為零，方差為的高斯白過程，繼續使用復值最小二乘cls框架改善了智能離散傅里葉變換sdft算法的性能，同樣，將此方法應用于非平衡系統信號上，基于cls的算法利用了序列的線性預測性質：然后最小化誤差e(n)的平方和：這里qk(m)是噪聲q(n)的dft變換；

組合l點序列定義向量相應的誤差向量為此誤差向量的共軛轉置形式可表示為cls框架作用在于找到一個最優的值以最小化均方誤差：令則提出的cls改進sdft的算法可以表示如下：

步驟4有噪條件下crphd實現進一步抗噪優化：

另一方面，重新考慮均方誤差值繼續推導如下：

這里是q(m)的方差，由于公式(6)的第二項是關于的噪聲項，一般情況下并不在取得最小值，這也是cls算法估計含噪信號的劣勢所在，在非平衡系統中使用復值rphd方法crphd，如公式(6)所示，為了移除噪聲對頻率估計誤差的影響，依據來最小化重新定義一個新的代價函數為：

步驟5尋求最優的值最小化計算求解頻率估計值：

為了找到最優的值最小化求偏導令其等于零：

這里：

盡管公式(8)的最后推導式有兩個根，但只有一個根可以表示頻率估計量，如此推導得到

了相對于cls更加抗噪的，適用于復值非圓信號的crphd頻率估計方法，如下所示：

本發明的進一步改進，步驟二，通過下面的方法根據xk(m+1),xk(m)和xk(m-1)的值可以估計k和δ；

1)基于dft最大點的位置進行頻率粗估計：

2)估計δ：定義公式(1)前一項為a(m)，第二項為b(m)，這樣公式(1)中的xk(m)表示為：xk(m)＝ak(m)+bk(m)。

本發明基于改進的smartdft算法的非平衡系統頻率估計方法，本申請擴展了原始的smartdft技術(sdft)，使此項技術不僅可以應用于實值正弦信號，也可以處理復值非圓信號。基于連續dft基頻分量間的線性預測(lp)性質，應用最小二乘框架可以減小模型的均方誤差。同時，提出了一種復值改進的pisarenko諧波分解算法(crphd)，此方法可以移除噪聲的干擾獲得精確的頻率估計。本發明在含有噪聲的非平衡三相電力系統中，經過仿真顯示本申請所提出算法的優越的抗噪性能。

附圖說明

圖1為不同信噪比下頻率估計算法的均方誤差對比圖；

圖2為兩種算法在頻率波動下的頻率跟蹤性能圖(a)系統頻率經歷頻率調制(b)系統頻率經歷了上升和下降；

圖3真實環境非平衡三相電力系統中的頻率估計效果圖(a)三相電壓幅值波動(b)頻率估計效果。

具體實施方式

下面結合附圖與具體實施方式對本發明作進一步詳細描述：

本發明提供基于改進的smartdft算法的非平衡系統頻率估計方法，擴展了原始的smartdft技術(sdft)，使此項技術不僅可以應用于實值正弦信號，也可以處理復值非圓信號。基于連續dft基頻分量間的線性預測(lp)性質，應用最小二乘框架可以減小模型的均方誤差，得到改進的復值最小二乘算法(cls)。同時，專利還提出了一種復值改進的pisarenko諧波分解算法(crphd),此方法可以移除噪聲的干擾獲得精確的頻率估計，可以有效應用在含有噪聲的非平衡三相電力系統中。

具體實施例1如下：

在這部分，我們將利用matlab平臺展示專利算法的仿真結果。我們分別設置采樣頻率為fs＝1600，基點頻率為f0＝50，這樣，為了計算dft的基礎頻率，系統電壓的采樣點需要設置為n＝fs/f0＝32。同時，我們將估計算法的窗長設置為l＝15。

首先，我們評估在噪聲環境下crphd算法相對于cls優越的估計性能。非平衡系統電壓真實頻率f＝f0+δf設置在51hz，將不同信噪比條件下的噪聲加入系統中，圖1展示了crphd和cls頻率估計算法的均方誤差，如圖所示，所提出的crphd算法在性能上與cls相似，但在低信噪比條件下，它的估計效果將優于cls算法。

具體實施例2如下：

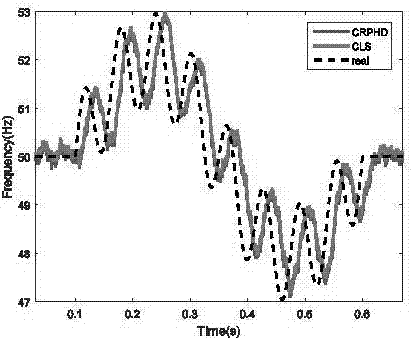
本組仿真，我們將研究在頻率波動情況下，不同估計算法的頻率跟蹤性能。在原始非平衡系統基礎上，信號在0.1s到0.6s經歷了復合的正弦頻率調制f(t)＝50+2sin(4π(t-0.1))+sin(32π(t-0.1))，這里ω0(t)＝2π·f(t)，同時系統加入10db噪聲。如圖2(a)所示，兩種算法都可以快速而又準確的跟蹤到系統頻率的動態變化。圖2(b)中，非平衡系統在t＝0s時加入40db的噪聲，同時系統頻率經歷了1hz/s的上升，然后在50.1hz處保持了0.2s，緊接著從0.5s到0.6s經歷了1hz/s的下降。在所有情況下，兩種算法都精準跟蹤到了頻率變化。

具體實施例3如下：

最后一組仿真，我們在真實世界電力系統下研究所提出算法的魯棒性。三相電壓信號記錄在110/20/10kv的變電站中。所要測量的三相電壓系統頻率大約在50hz附近，經過了1khz的采樣，電壓幅值根據峰值進行了歸一化處理。在圖3(a)中，所示電壓在0.27s至0.54s左右經歷了非平衡狀態，如圖3(b)所示，雖然出現了短暫的波動，兩種算法在平衡和非平衡電壓情況下都獲得了準確的頻率估計效果。

以上所述，僅是本發明的較佳實施例而已，并非是對本發明作任何其他形式的限制，而依據本發明的技術實質所作的任何修改或等同變化，仍屬于本發明所要求保護的范圍。