本發明涉及一種故障診斷技術，特別涉及一種基于改進多尺度模糊熵的滾動軸承故障診斷方法。

背景技術：

滾動軸承是旋轉機械中關鍵的部件之一，其運行狀態往往決定著整臺機器的性能。因此，滾動軸承的故障診斷有重要的意義。在各種軸承故障診斷方法中，基于振動信號的診斷是最常用、最有效的方法之一。而滾動軸承在運行過程中難免會受到摩擦、間隙和非線性剛度等非線性因素的影響，所采集的振動信號往往呈現出很強的非線性、非穩態特征。因此，傳統的基于線性系統的時域和時頻域信號分析方法很難準確地提取軸承的故障特征信息。隨著非線性動力學的發展，出現了一些非線性動力學分析技術，為分析軸承復雜的非線性動力學行為提供了一種很好的選擇。這其中近似熵、樣本熵、多尺度熵和多尺度模糊熵等都被引入到滾動軸承的故障診斷中，并取得了很好的診斷效果。近似熵是對時間序列復雜度的一種度量，樣本熵是對近似熵的一種改進，減少了對序列長度依賴的同時克服了近似熵自身匹配的缺點。模糊熵是把模糊集的概念引入到樣本熵的計算中，其對參數的依賴性更小、相對一致性更強且抗噪能力更好。多尺度模糊熵是定義在不同尺度下的模糊熵，用來衡量時間序列在不同尺度下的復雜性，比單一尺度的模糊熵能更全面的衡量信號的復雜度。

然而，模糊熵在構建計算所需的向量時減去了一個局部均值，這使得在計算熵值時忽略了信號的整體趨勢。而對于滾動軸承的故障診斷而言，只有全面考慮振動信號所包含的特征，才能提取可以更加全面地反映軸承運行狀態的故障特征信息。

技術實現要素：

本發明是針對傳統的多尺度模糊熵算法在提取軸承狀態信息時存在局限的問題，提出了一種基于改進多尺度模糊熵的滾動軸承故障診斷方法，對模糊熵算法進行改進，用一個總體均值代替的傳統模糊熵計算中的局部均值，計算不同尺度下的改進模糊熵。改進后的多尺度模糊熵能更全面地反映信號的特征，從而更準確地評估軸承的運行狀態。

本發明的技術方案為：一種基于改進多尺度模糊熵的滾動軸承故障診斷方法，具體包括如下步驟：

1)、測量滾動軸承的振動信號；

2)、計算軸承振動信號的改進多尺度模糊熵：

對測量得到的軸承振動信號進行粗粒化；針對模糊熵計算過程中存在的局限性，對模糊熵算法進行改進；計算不同尺度因子下粗粒序列的改進模糊熵，改進模糊熵算法點為利用總體均值代替原模糊熵算法公式中的局部均值u0(i)，即對于一個n點時間序列{u(i):1≤i≤n},構建一個m維向量

其中，表示從第i點開始的連續m個u值減去總體均值

3)、選取前八個尺度上的改進模糊熵作為軸承故障特征向量；

4)、將得到的軸承故障特征分為訓練樣本和測試樣本；

5)、利用訓練樣本對支持向量機進行訓練得到預測模型；

6)、利用得到的預測模型對測試樣本進行預測；

7)、根據預測結果識別滾動軸承的工作狀態與故障類型。

本發明的有益效果在于：本發明基于改進多尺度模糊熵的滾動軸承故障診斷方法，改進傳統的模糊熵算法，能夠提取更加豐富的軸承狀態信息，在故障模式識別過程中有更高的識別率。

附圖說明

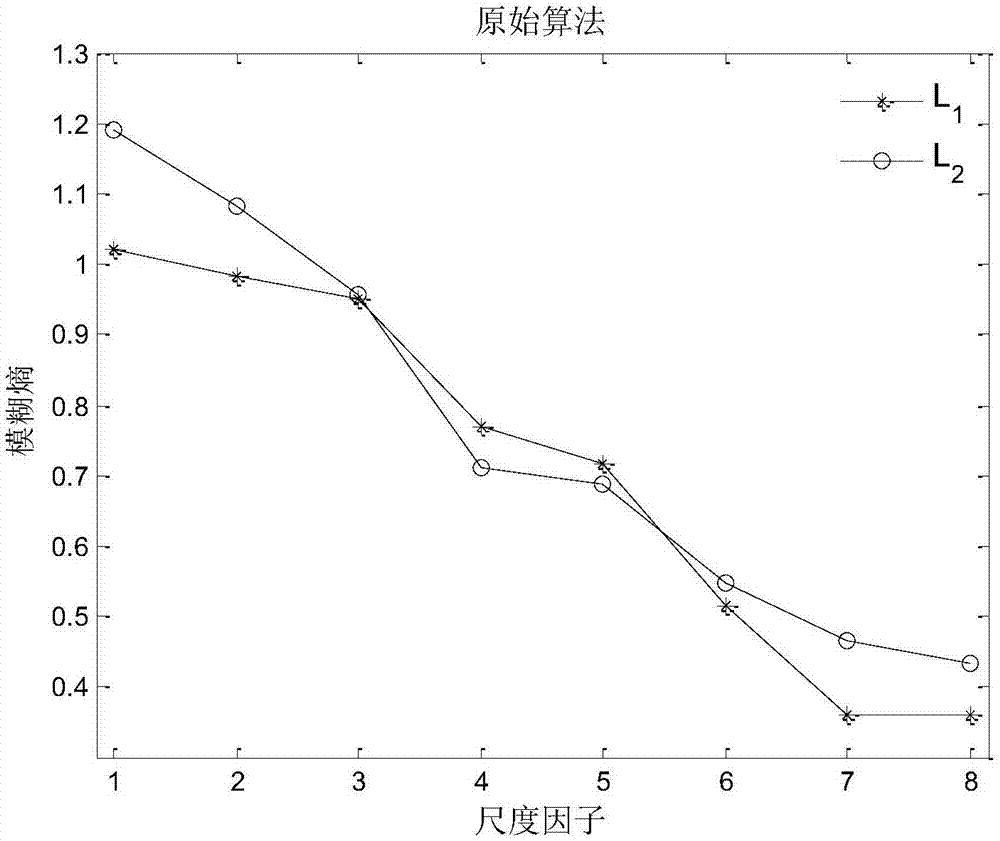
圖1為模擬信號原始算法的多尺度熵分析圖；

圖2為本發明模擬信號改進算法的多尺度熵分析圖；

圖3為本發明十種不同軸承故障在八個不同尺度上的改進模糊熵圖；

圖4為本發明基于改進多尺度模糊熵和支持向量機的滾動軸承故障診斷流程圖；

圖5為本發明基于改進多尺度模糊熵和svm的識別結果圖；

圖6為基于原始多尺度模糊熵和svm的識別結果圖。

具體實施方式

本發明為了克服傳統的模糊熵在計算時忽略信號的整體趨勢這一局限，同時為了提高故障診斷效率，減少人為因素對診斷結果的干擾，提供了一種基于改進的多尺度模糊熵和支持向量機的滾動軸承故障診斷方法，具體采用以下技術方案：

1.改進的多尺度熵算法

1.1多尺度模糊熵

近似熵和樣本熵都是基于heaviside函數(單位階躍函數)來定義向量的相似性的，導致了傳統的二值分類的結果，而現實世界中類的邊界是模糊的，很難直接確定一個待定模式是否完全屬于某一類。模糊熵引入了模糊集的概念，利用指數函數作為模糊函數來計算向量的相似性。

模糊熵的定義如下：

(1)對于一個n點時間序列{u(i):1≤i≤n},構建一個m維向量

其中，表示從第i點開始的連續m個u值減去局部均值u0(i)，

其中

(2)定義和之間的距離為兩者對應元素的最大差值

(3)利用模糊函數定義和的相似度為

r為相似容限，即相似度為兩者對應元素的最大差值和相似容限的函數；

(4)對每一個把其與所有的相似度平均，表示為

(5)定義函數為

(6)類似地，對m+1維，重復上面的步驟得

(7)定義模糊熵為

(8)當n為有限值時，(8)式可以表示為

fuzzyen(m,r,n)＝lnφ^m(r)-lnφ^m+1(r)(9)

模糊熵最初選擇作為模糊函數的指數函數為

為了使指數函數有更明確的物理意義，式(10)進行了如下改進

本文使用(11)式來計算模糊熵。

模糊熵和樣本熵一樣，都是對時間序列復雜度在單一尺度上的度量，熵值越大，序列的復雜度越高。為了衡量時間序列在不同尺度下的復雜性和自相似性，構造原始時間序列的粗粒化序列如下：

其中，τ代表尺度因子，1＜＜j＜＜n/τ。實際上，當τ＝1時,即為原序列。對非零τ原始時間序列被分割為τ個每段長度為n/τ的粗粒序列計算不同尺度下粗粒序列的模糊熵，即為多尺度模糊熵分析。如果一個時間序列在大部分尺度上的熵值都比另一個序列大，那么代表前者有更高的復雜度。

1.2改進的多尺度模糊熵

然而，模糊熵在構建計算相似性的向量時，減去了一個均值，這樣設計的目的是為了能更準確地描述短暫生理電信號中發生的局部相似性，但這卻忽略了信號的整體趨勢。而對于滾動軸承的性能退化評估而言，只有全面考慮振動信號所包含的特征，才能更加全面地反映軸承運行的狀態。基于上面的分析，本文在計算時利用總體均值代替公式(1)中的局部均值u0(i)，改為

其中，定義如下：

然后用(13)式計算模糊熵，并用改進后的模糊熵算法和多尺度分析相結合計算軸承振動信號，進行改進的多尺度模糊熵分析。模擬信號以及實際軸承疲勞壽命加速試驗數據驗證了改進后的多尺度模糊熵的有效性和優越性。

1.3參數的選擇

根據模糊熵的定義，模糊熵值的計算取決于嵌入維數m、相似容限r、序列長度n以及模糊函數的梯度n。嵌入維數m表示比較窗口的長度，r代表相似容限的寬度。m值越大，重構系統的發展過程就越細致，然而大的m值需要足夠的數據長度(n＝10^m～30^m)，或者相似容限足夠大。但是相似容限過大會導致丟掉很多統計信息，反過來相似容限過小又會增加計算結果對噪聲的敏感性。一般r的取值范圍是0.1～0.25sd(sd為原始序列的標準差)。綜合考慮，本發明取m＝2，r＝0.2sd，n＝2048。與樣本熵相比，模糊熵的計算還多了一個參數n，它決定著相似容限邊界的梯度。n在計算向量相似性過程中起著權重的作用，當n>1時，更多地計入較近的向量對其相似度的貢獻，而更少地計入較遠的向量的相似度貢獻；當n<1時，效果則相反。過大的n會喪失細節信息，當n為無窮大時，指數函數退化為heaviside函數，此時會喪失邊緣的全部細節信息。因此，為了獲取盡量多的細節信息，n取較小的整數值，如2或3等，本發明取n＝2。

2.模擬信號的分析

利用模擬信號初步驗證原始算法與改進后算法對不同復雜度信號的分辨能力，模擬信號由一個邏輯序列l、一個正弦信號s和一個隨機信號r組成：

lj＝l+aj×(s+r)

式中a表示s與l的幅值比，l代表由下式生產的邏輯序列：

x(n+1)＝ω×x(n)×(1-x(n))

ω是決定序列復雜度的常數，改變不同的a和ω可以得到不同復雜度的模擬信號。當取a1＝a2＝0.1，ω1＝3.7，ω2＝3.8時可知，其對應信號的復雜度滿足這樣的關系：l1<l2。圖1是原始算法的多尺度熵分析，計算了前八個尺度的模糊熵，由圖可知，l2在一些尺度上(τ＝1,2,3,6,7,8)的熵值大于l1，但是在τ＝4和5時，熵值小于l1，這在進行l1和l2的復雜度分析時會造成混亂。作為對比，圖2是改進算法的多尺度熵分析，從圖中可以看到，l2在8個尺度上的熵值都大于l1。因此，與原始算法相比，改進的多尺度模糊熵對信號復雜度具有更好的區分能力。

3.實例驗證

為了進一步說明改進多尺度模糊熵在提取滾動軸承故障特征的有效性，對實際的軸承試驗數據進行了分析。同時，為了實現故障診斷的智能化并降低人為因素對故障識別結果的影響，建立了基于支持向量機的多故障分類器來實現不同軸承故障的自動診斷。支持向量機算法簡單，泛化能力強，在小樣本分類中表現優異，被廣泛應用于故障診斷領域。

3.1試驗數據

本文采用的試驗數據來自于美國凱斯西儲大學的軸承數據中心，測試軸承型號為skf6205-2rsjem深溝球軸承，利用電火花加工技術布置故障尺寸不同的單點故障。軸承轉速為1797r/min，采樣頻率為12khz，包含正常狀態、內圈故障、外圈故障和滾動體故障以及不同故障尺寸共10種故障類型，每個數據長度為2048點，具體如表1所示試驗數據集。

表1

3.2試驗結果與分析

利用改進的多尺度模糊熵分析上述十種不同滾動軸承狀態下振動數據，結果如圖3所示。從圖中可以看出，正常狀態下信號在不同尺度上的改進模糊熵變化趨勢與故障信號不同，故障狀態下信號的熵值隨著尺度的增大呈現明顯的下降趨勢，而正常信號隨著尺度的增加先增大然后逐漸趨于平穩，在大部分尺度上的熵值都比故障信號大，說明正常狀態下信號的復雜度比故障信號高。這是因為當正常運行在健康狀態下時，振動是隨機的、不規則的，主要來自于機械零部件之間的相互作用、耦合以及環境噪聲，因此，正常信號有比較低的自相似度，高的復雜度。相對地，當軸承出現故障時，由故障引起的沖擊會帶來很多確定性的沖擊成分，從而增加了故障信號的自相似性，降低了其復雜度。從圖3還可以看出，雖然不同故障狀態下的信號在不同尺度下有相似的變化趨勢，但是不同的故障狀態在不同尺度上的熵值大小不同，說明不同的故障狀態下信號的復雜度不同，因此，改進后的多尺度模糊熵是一種有效的反映和區分滾動軸承故障特征的方法。

為了降低人為因素對故障識別結果的影響，并且驗證改進的多尺度模糊熵相對于原始算法的多尺度模糊熵在提取軸承狀態信息時的優越性，支持向量機被用來實現滾動軸承故障的自動診斷。由于進行多類分類，本發明采用一對一的方法建立多分類支持向量機。核函數選用徑向基核函數，利用交叉驗證和網格搜索的方法尋找最優的懲罰參數和核函數參數。利用改進多尺度模糊熵和支持向量機的滾動軸承故障診斷步驟如圖4所示。具體包括如下步驟：

步驟(1)、測量滾動軸承的振動信號；

步驟(2)、計算軸承振動信號的改進多尺度模糊熵：

對測量得到的軸承振動信號進行粗粒化；針對模糊熵計算過程中存在的局限性，對模糊熵算法進行改進；計算不同尺度因子下粗粒序列的改進模糊熵，計算模糊熵采用上述公式(13)和(14)；

步驟(3)、選取前八個尺度上的改進模糊熵作為軸承故障特征向量；

步驟(4)、將得到的軸承故障特征分為訓練樣本和測試樣本；

步驟(5)、利用訓練樣本對支持向量機進行訓練得到預測模型；

步驟(6)、利用得到的預測模型對測試樣本進行預測；

步驟(7)、根據預測結果識別滾動軸承的工作狀態與故障類型。

十種軸承狀態每種狀態選取50組數據，考慮實際中故障樣本很難得到，其中10組用于訓練，其余40組用來測試，一共500組數據。把訓練樣本輸入支持向量機進行訓練，用訓練好的模型預測測試數據，所有的訓練樣本都被正確識別，測試樣本的識別結果如圖5所示，400組測試樣本只有3個被錯分，預測準確率為99.25％。為了突出改進多尺度熵算法的優越性，計算了上述數據的原始多尺度熵，利用同樣的步驟訓練并建立支持向量機預測模型，然后對測試數據進行分類識別。所有的訓練樣本都被正確識別，測試樣本的識別結果見圖6，400組測試樣本一共有14個被錯分，分類準確率為96.5％。這一對比結果也說明了改進后的多尺度模糊熵比原始算法能夠更有效地提取隱含在軸承振動信號里的狀態信息，因而能更準確地識別不同的軸承故障狀態。