本發明涉及配電網優化技術領域，具體地說，涉及一種變壓器轉移負荷的控制方法。

背景技術：

變壓器油是石油的一種分餾產物，它的主要成分是烷烴,環烷族飽和烴，芳香族不飽和烴等化合物。變壓器油具有散熱作用，變壓器油的比熱大，常用作冷卻劑。變壓器運行時產生的熱量使靠近鐵芯和繞組的油受熱膨脹上升，通過油的上下對流，熱量通過散熱器散出，保證變壓器正常運行。

現有技術中，常使用變壓器油溫來指示變壓器的溫度，當變壓器溫度過高時，可將油溫較高的變壓器的負荷向油溫較低的變壓器轉移，從而降低變壓器油溫。然而，當變壓器內部的組件例如繞組或鐵芯溫度升高時，變壓器的油溫并不會立即升高，變壓器的油溫與變壓器內部組件的溫度達到穩定需要一定的延時，因此若測得變壓器油溫過高時再進行負荷的轉移，變壓器內部的組件溫度可能已經過高，存在安全隱患。

技術實現要素：

針對上述現有技術的不足，本發明提供了一種變壓器轉移負荷的控制方法，對變壓器的油溫進行預測，建立變壓器轉移負荷的目標函數，并求目標函數的最優解，實現對變壓器負荷的轉移。與現有技術相比，基于變壓器的預測油溫進行負荷轉移，避免了油溫與變壓器內部組件達到穩定前變壓器內部組件溫度過高造成的安全隱患，提高了變壓器運行的安全性。

為了解決上述技術問題，本發明采用了如下的技術方案：

一種變壓器轉移負荷的控制方法，所述方法用于控制220kv變壓器向110kv變壓器轉移負荷，所述方法包括：

預測第t時段的220kv變壓器油溫變化量δθ(t)，δp(t)為220kv變壓器在第t時段的功率增量，δθ(t)＝a(t)δp(t)+b(t)；

建立目標函數：

為第t時段優化后110kv線路開關j的狀態，0表示開關是拉開狀態，1表示開關是運行狀態；為第t時段優化前110kv線路開關的狀態；第t個時段的始端時刻為當前時刻，即t-1時刻，第t個時段的末端時刻為未來時刻，即t時刻；ns表示總的110kv線路開關個數；a(t)為第t時段nt臺220kv變壓器溫度變化量函數的1×nt階斜率向量，diag[a(t)]表示把列向量a(t)變成對角矩陣；θ(t)和b(t)為第t時段監控系統獲取的當前時刻變壓器油溫及所述220kv變壓器油溫變化量δθ(t)系數的nt×1階向量，pgmax和θmax為220kv變壓器的最大功率和上層油溫允許值的nt×1階向量；為在時段t時與第i個220kv變壓器與110kv線路開關存在拓撲關系的負荷系數行向量，st為開關狀態列向量；

利用目標算法計算所述目標函數求出最優解；

基于所述最優解控制220kv變壓器轉移負荷。

優選地，所述220kv變壓器油溫變化量δθ(t)包括自然狀態下變壓器油溫變化量δθup(t)，

式中：δθa(t)為環境溫度變化量，sn為220kv變壓器額定容量；自然狀態油溫變化率dδθup(t)/dt＝[δθup(t)-δθup(t-1)]/δt＝[θup(t)-2θup(t-1)+θup(t-2)]/δt，δt為相鄰時段時間間隔，t-2表示t-1時刻之前一個時間段的時刻，rath為220kv變壓器空氣側的等效熱阻，roth為220kv變壓器油側的等效熱阻，cth為220kv變壓器的等值熱容，x為油指數，p0為220kv變壓器的空載損耗，pk為220kv變壓器的短路損耗。

優選地，所述220kv變壓器空氣側的等效熱阻rath、所述220kv變壓器油側的等效熱阻roth、所述220kv變壓器的等值熱容cth及所述油指數x的計算方法為，分別設x、rath、roth、cth為x1、x2、x3、x4，式(1)中的p(t)、δp(t)、δθa(t)、δθup(t)、dδθup(t)/dt可由歷史數據算出，分別設為y1、y2、y3、y4、y5，設有n組數據，則第i組為y1(i)、y2(i)、y3(i)、y4(i)、y5(i)，將式子所述變壓器油溫變化量δθup(t)的計算公式改寫成如下形式：

y4＝g1(x1，x2，x3，x4，y1，y2，y3，y5)

而實際中由于存在誤差，左右并不相等，設誤差為w，y1、y2、y3、y4、y5、w為n維列向量，

y4＝g1(x1，x2，x3，x4，y1，y2，y3，y5)+w，

根據最小二乘法，有z1＝[y4-g1(x1，x2，x3，x4，y1，y2，y3，y5)]^t·[y4-g1(x1，x2，x3，x4，y1，y2，y3，y5)]，y1、y2、y3、y4、y5是由歷史統計數據得到，為已知量；x1，x2，x3，x4為未知量，z1是關于x1，x2，x3，x4的函數，求出z1取最小值時的x1，x2，x3，x4的取值就為對x、rath、roth、cth的最佳估計。

優選地，所述220kv變壓器油溫變化量δθ(t)包括人工降溫狀態下變壓器油溫變化量δθdown(t)，

式中：sn為220kv變壓器額定容量；自然狀態油溫變化率dδθdown(t)/dt＝[δθdown(t)-δθdown(t-1)]/δt＝[θdown(t)-2θdown(t-1)+θdown(t-2)]/δt，δt為相鄰時段時間間隔，t-2表示t-1時刻之前一個時間段的時刻，rath為220kv變壓器空氣側的等效熱阻，roth為220kv變壓器油側的等效熱阻，cth為220kv變壓器的等值熱容，x為油指數，p0為220kv變壓器的空載損耗，pk為220kv變壓器的短路損耗，冷源的溫度變化量δθi(t)＝θi(t)-θi(t-1)，rir為人工降溫側的等效熱阻，ca為人工降溫側的等值熱容。

優選地，所述220kv變壓器空氣側的等效熱阻rath、所述220kv變壓器油側的等效熱阻roth、所述220kv變壓器的等值熱容cth、所述油指數x、所述人工降溫側的等效熱阻rir及所述人工降溫側的等值熱容ca的計算方法為，分別設x、rath、roth、cth、ca、rir為x1，x2，x3，x4，x5，x6，所述人工降溫狀態下變壓器油溫變化量δθdown(t)的計算公式中的p(t)、δp(t)、δθi(t)、δθdown(t)、dδθdown(t)/dt、dδθa(t)/dt可由歷史數據算出，分別設為y1、y2、y3、y4、y5、y6，設有n組數據，則第i組為y1(i)、y2(i)、y3(i)、y4(i)、y5(i)、y6(i)，將所述人工降溫狀態下變壓器油溫變化量δθdown(t)的計算公式改寫成如下形式：

y4＝g2(x1，x2，x3，x4，y1，y2，y3，y5，y6)，

而實際中由于存在誤差，左右并不相等，設誤差為w，y1、y2、y3、y4、y5、y6、w為n維列向量，

y4＝g2(x1，x2，x3，x4，y1，y2，y3，y5，y6)+w，

根據最小二乘法，有z2＝[y4-g2(x1，x2，x3，x4，x5，x6，y1，y2，y3，y5，y6)]^t·

[y4-g2(x1，x2，x3，x4，x5，x6，y1，y2，y3，y5，y6)]，

y1、y2、y3、y4、y5、y6是由歷史統計數據得到，為已知量；x1，x2，x3，x4、x5、x6為未知量，z2是關于x1，x2，x3，x4，x5，x6的函數，求出z2取最小值時的x1，x2，x3，x4，x5，x6的取值就為對x、rath、roth、cth、ca、rir的最佳估計。

綜上所述，本技術方案提供了一種變壓器轉移負荷的控制方法，所述方法用于控制220kv變壓器向110kv變壓器轉移負荷，所述方法包括，預測第t時段的220kv變壓器油溫變化量δθ(t)，建立目標函數，利用目標算法計算目標函數求出最優解。對變壓器的油溫進行預測，建立變壓器轉移負荷的目標函數，并求目標函數的最優解，實現對變壓器負荷的轉移。與現有技術相比，基于變壓器的預測油溫進行負荷轉移，避免了油溫與變壓器內部組件達到穩定前變壓器內部組件溫度過高造成的安全隱患，提高了變壓器運行的安全性。

附圖說明

為了使發明的目的、技術方案和優點更加清楚，下面將結合附圖對本發明作進一步的詳細描述，其中：

圖1為本發明公開的一種變壓器轉移負荷的控制方法的實施例1的流程圖；

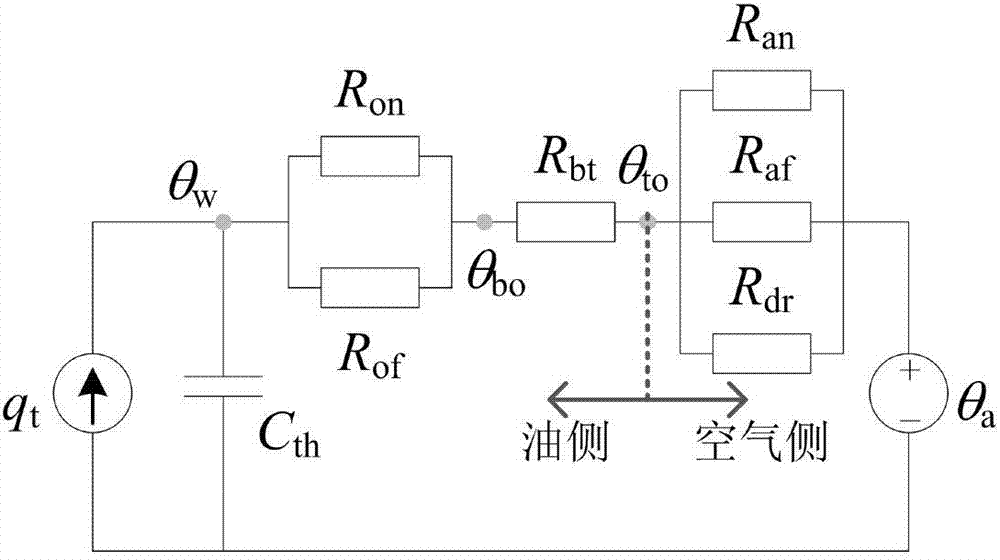
圖2為自然狀態的變壓器的電路結構示意圖；

圖3為自然狀態的變壓器的簡化電路結構示意圖；

圖4為人工降溫狀態的變壓器的簡化電路結構示意圖；

圖5為一種變壓器間連接關系的結構示意圖；

圖6為另一種變壓器間連接關系的結構示意圖。

具體實施方式

下面結合附圖對本發明作進一步的詳細說明。

在本發明中所指的變壓器油溫指的是變壓器的上層油溫(頂層油溫)。

如圖1所示，為本發明公開的一種變壓器轉移負荷的控制方法的實施例1的流程圖，其特征在于，所述方法用于控制220kv變壓器向110kv變壓器轉移負荷，所述方法包括：

s101、預測第t時段的220kv變壓器油溫變化量δθ(t)，δp(t)為220kv變壓器在第t時段的功率增量，δθ(t)＝a(t)δp(t)+b(t)；

為保證220kv變壓器的油溫不過高，因此，需要滿足θ′(t)＝θ(t)+a(t)δp(t)+b(t)≤θmax，其中θ′(t)為預測的油溫，θmax為允許的最大油溫。

s102、建立目標函數：

以改變和恢復電網運行方式的遠方操作次數作為優化模型的目標函數，即以轉移負荷過程中變壓器間開關狀態的變化次數作為目標函數，可得：

其中式中：為第t時段優化后110kv線路開關j的狀態，0表示開關是拉開狀態，1表示開關是運行狀態；為第t時段優化前110kv線路開關的狀態；第t個時段的始端時刻為當前時刻，t-1時刻，第t個時段的末端時刻為未來時刻，t時刻。ns表示總的110kv線路開關個數。

如圖5及圖6所示，為兩種變壓器間連接關系的結構示意圖。圖5為直供接線方式，圖6為串供接線方式。圖5中110kv的c變壓器、220kv的a和b變壓器的接線方式是一供一備，即其中1個220kv變壓器對110kv的c變壓器負荷pc供電，另外1個220kv變壓器對其提供備用電源。可見圖中等效前接線的220kv變壓器側線路開關應是運行狀態，而110kv變壓器側的線路開關可為熱備用狀態，也可為運行狀態。對圖5中110kv變壓器直供接線方式而言，110kv變壓器側的線路開關s^t1和s^t2才是電網轉供模型的優化對象。對于110kv變壓器直供的接線方式，可得其功率平衡方程為，

其中分別代表a、b變壓器優化后帶的負荷。線路開關s^t1和s^t2取0表示斷開，取1表示閉合。pc表示c變壓器優化后的負荷。

同理，對圖6列寫功率平衡方程，

可以將功率平衡方程歸納成如下形式，并且每臺變壓器所帶負荷不能超過額定負荷最大值，

式中：為在時段t時與第i個220kv變壓器與110kv變壓器開關存在拓撲關系的負荷系數行向量，s^t為開關狀態列向量。

設第t時段優化前的開關狀態為s^0,t，優化后的開關狀態s^t，根據功率平衡方程式(14)可知優化前后各臺變壓器所帶功率的改變量為，

由于電網保護與運行方式的配合，110kv及以下電網須為輻射型開環運行，即受端電網的轉供優化中還需考慮110kv電網結構的輻射型約束。則第t時段110kv線路開關狀態s^t應滿足，

由上述式子即可求出

為第t時段優化后110kv線路開關j的狀態，0表示開關是拉開狀態，1表示開關是運行狀態；為第t時段優化前110kv線路開關的狀態；第t個時段的始端時刻為當前時刻，即t-1時刻，第t個時段的末端時刻為未來時刻，即t時刻；ns表示總的110kv線路開關個數；a(t)為第t時段nt臺220kv變壓器溫度變化量函數的1×nt階斜率向量，diag[a(t)]表示把列向量a(t)變成對角矩陣；θ(t)和b(t)為第t時段監控系統獲取的當前時刻變壓器油溫及220kv變壓器油溫變化量δθ(t)系數的nt×1階向量，pgmax和θmax為220kv變壓器的最大功率和上層油溫允許值的nt×1階向量；為在時段t時與第i個220kv變壓器與110kv線路開關存在拓撲關系的負荷系數行向量，st為開關狀態列向量。

s103、利用目標算法計算目標函數求出最優解；

目標算法可以為牛頓迭代法。

s104、基于最優解控制220kv變壓器轉移負荷；

最優解中包括了優化后每個開關的狀態以及變壓器負荷，利用最優解可以實現對變壓器的負荷的轉移。

220kv變壓器所帶負荷增加后，可以通過測得的電流電壓計算出功率，進而計算得到功率增量δp(t)，而后可以計算油溫的增量，判斷油溫是否會超過允許的最大油溫θmax。如果超過，就需要通過開關操作調整網絡拓撲結構，使負荷在各變電站主變之間重新分配，而我們希望在滿足約束條件的狀況下使開關操作次數最少，這一操作后的開關狀態為最優解。因此可使用牛頓迭代法對目標函數進行求解。

綜上所述，本技術方案提供了一種變壓器轉移負荷的控制方法，所述方法用于控制220kv變壓器向110kv變壓器轉移負荷，所述方法包括，預測第t時段的220kv變壓器油溫變化量δθ(t)，建立目標函數，利用目標算法計算目標函數求出最優解，目標算法包括牛頓迭代法。對變壓器的油溫進行預測，建立變壓器轉移負荷的目標函數，并求目標函數的最優解，實現對變壓器負荷的轉移，基于最優解控制220kv變壓器轉移負荷。與現有技術相比，基于變壓器的預測油溫進行負荷轉移，避免了油溫與變壓器內部組件達到穩定前變壓器內部組件溫度過高造成的安全隱患，提高了變壓器運行的安全性。

如圖2及圖3所示，為自然狀態的變壓器的電路結構示意圖及自然狀態的變壓器的簡化電路結構示意圖，自然狀態即變壓器通過強迫油循環風冷進行散熱，如圖2所示，其中變壓器繞組熱源由電流源qt等值，包括繞組、鐵心和雜散損耗；cth為變壓器內絕緣油、繞組和油箱等組成的等值熱容，物體的等值熱容與其比熱成正比；ron、rof為變壓器熱量傳遞至絕緣油的自然換流和強迫換流熱阻；rbt為常規的強迫油循環方式下不同溫度絕緣油相混合對應的熱阻，而強迫油循環導向冷卻方式下，泵口的冷油在一定壓力下送入線圈、線餅和鐵心的油道，內部油溫分布更加均勻，此時近似認為rbt＝0；rdr為散熱器向周圍空氣傳熱的輻射熱阻，ran和raf為風冷散熱中空氣自然對流及強迫對流的熱阻。熱阻表示的兩點間熱量傳遞的劇烈程度。相同溫差下，熱阻越小，傳遞熱量的過程越劇烈，即兩者間的熱傳遞功率越大。θw為繞組溫度，θa為環境溫度，θto代表變壓器頂層油溫。在熱電等值電路中電位代表溫度，兩點之間溫差越大，則電路中電位差越大。

由圖2可得變壓器內部的熱傳遞過程，熱源通過自然換流和強迫換流將熱量傳遞給上層油層，而變壓器內部的絕緣油在強迫循環中，當其循環到散熱器，通過風扇鼓動空氣將其降溫。因此熱阻主要包括油側熱阻和空氣側熱阻兩部分，可以將圖2簡化成圖3。根據圖3列寫油溫的狀態方程：

上式由基爾霍夫電流定律得出，變壓器的熱源為與空載損耗、短路損耗和負荷系數相關的函數qt＝(p0+k²p^k)^x。對上式進行泰勒展開，可得油溫增量與負荷率k增量之間的關系：

其中p0，pk可以通過銘牌參數得到，δθa、δk、δθto、dδθto/dt、k0分別代表環境溫度的改變量、負荷率的改變量、油溫的改變量、油溫改變量變化率和前一時刻的負荷率，可以根據歷史數據得到以上各量，然后再根據非線性最小二乘法估計出參數x、cth、roth、rath，最后根據當前測得環境溫度與負荷率改變量即可預測出油溫的改變量。

負荷率k＝p/sn，p代表變壓器的實際承受的功率，sn代表變壓器的額定容量。將負荷率k表示成p/sn，可以將式(6)轉化成式自然狀態下變壓器油溫變化量δθup(t)，

式中：δθa(t)為環境溫度變化量，sn為220kv變壓器額定容量；自然狀態油溫變化率dδθup(t)/dt＝[δθup(t)-δθup(t-1)]/δt＝[θup(t)-2θup(t-1)+θup(t-2)]/δt，δt為相鄰時段時間間隔，t-2表示t-1時刻之前一個時間段的時刻。rath為220kv變壓器空氣側的等效熱阻，roth為220kv變壓器油側的等效熱阻，cth為220kv變壓器的等值熱容，x為油指數，p0為220kv變壓器的空載損耗，pk為220kv變壓器的短路損耗。

220kv變壓器空氣側的等效熱阻rath、220kv變壓器油側的等效熱阻roth、220kv變壓器的等值熱容cth及油指數x的計算方法為，分別設x、rath、roth、cth為x1、x2、x3、x4。式(1)中的p(t)、δp(t)、δθa(t)、δθup(t)、dδθup(t)/dt可由歷史數據算出，分別設為y1、y2、y3、y4、y5，設有n組數據，則第i組為y1(i)、y2(i)、y3(i)、y4(i)、y5(i)，將式子變壓器油溫變化量δθup(t)的計算公式改寫成如下形式：

y4＝g1(x1，x2，x3，x4，y1，y2，y3，y5)

而實際中由于存在誤差，左右并不相等，設誤差為w，y1、y2、y3、y4、y5、w為n維列向量，

y4＝g1(x1，x2，x3，x4，y1，y2，y3，y5)+w，

根據最小二乘法，有z1＝[y4-g1(x1，x2，x3，x4，y1，y2，y3，y5)]^t·[y4-g1(x1，x2，x3，x4，y1，y2，y3，y5)]，y1、y2、y3、y4、y5是由歷史統計數據得到，為已知量；x1，x2，x3，x4為未知量，z1是關于x1，x2，x3，x4的函數。求出z1取最小值時的x1，x2，x3，x4的取值就為對x、rath、roth、cth的最佳估計，具體求最值的方法有牛頓迭代法、內點法等最優化方法。

如圖4所示，為人工降溫狀態的變壓器的簡化電路結構示意圖，圖中人工冷源的溫度為θi，ca為空氣的等值熱容，rir為冷源向周圍空氣傳熱的輻射熱阻。在等值電路中空氣側運用基爾霍夫電流定律可得空氣溫度θa的狀態方程：

對上式泰勒展開，可得增量表達式：

將式(8)帶入式(6)可得

將上式的負荷率k用功率表示，可得到人工降溫狀態下變壓器油溫變化量δθdown(t)，

式中：sn為220kv變壓器額定容量；自然狀態油溫變化率dδθdown(t)/dt＝[δθdown(t)-δθdown(t-1)]/δt＝[θdown(t)-2θdown(t-1)+θdown(t-2)]/δt，δt為相鄰時段時間間隔，t-2表示t-1時刻之前一個時間段的時刻，rath為220kv變壓器空氣側的等效熱阻，roth為220kv變壓器油側的等效熱阻，cth為220kv變壓器的等值熱容，x為油指數，p0為220kv變壓器的空載損耗，pk為220kv變壓器的短路損耗，冷源的溫度變化量δθi(t)＝θi(t)-θi(t-1)，rir為人工降溫側的等效熱阻，ca為人工降溫側的等值熱容。

220kv變壓器空氣側的等效熱阻rath、220kv變壓器油側的等效熱阻roth、220kv變壓器的等值熱容cth、油指數x、人工降溫側的等效熱阻rir及人工降溫側的等值熱容ca的計算方法為，分別設x、rath、roth、cth、ca、rir為x1，x2，x3，x4，x5，x6，人工降溫狀態下變壓器油溫變化量δθdown(t)的計算公式中的p(t)、δp(t)、δθi(t)、δθdown(t)、dδθdown(t)/dt、dδθa(t)/dt可由歷史數據算出，分別設為y1、y2、y3、y4、y5、y6，設有n組數據，則第i組為y1(i)、y2(i)、y3(i)、y4(i)、y5(i)、y6(i)，將人工降溫狀態下變壓器油溫變化量δθdown(t)的計算公式改寫成如下形式：

y4＝g2(x1，x2，x3，x4，y1，y2，y3，y5，y6)，

而實際中由于存在誤差，左右并不相等，設誤差為w，y1、y2、y3、y4、y5、y6、w為n維列向量，

y4＝g2(x1，x2，x3，x4，y1，y2，y3，y5，y6)+w，

根據最小二乘法，有z2＝[y4-g2(x1，x2，x3，x4，x5，x6，y1，y2，y3，y5，y6)]^t·

[y4-g2(x1，x2，x3，x4，x5，x6，y1，y2，y3，y5，y6)]，

y1、y2、y3、y4、y5、y6是由歷史統計數據得到，為已知量；x1，x2，x3，x4、x5、x6為未知量，z2是關于x1，x2，x3，x4，x5，x6的函數，求出z2取最小值時的x1，x2，x3，x4，x5，x6的取值就為對x、rath、roth、cth、ca、rir的最佳估計，具體求最值的方法有牛頓迭代法、內點法等最優化方法。

為保證變壓器的油溫在安全范圍內，因此，需要滿足：

θ′up(t)＝θup(t)+aup(t)δp(t)+bup(t)≤θmax(10)

θ′down(t)＝θdown(t)+adown(t)δp(t)+bdown(t)≤θmax(11)

最后說明的是，以上實施例僅用以說明本發明的技術方案而非限制，盡管通過參照本發明的優選實施例已經對本發明進行了描述，但本領域的普通技術人員應當理解，可以在形式上和細節上對其作出各種各樣的改變，而不偏離所附權利要求書所限定的本發明的精神和范圍。