本發明屬于地球科學研究領域，特別涉及遙感地學空間統計分析和模式識別等方面，具體涉及基于區域不一致性評價自動優選遙感影像分割參數的方法。

背景技術：

在遙感領域，針對不同應用和目的，不同的影像分割算法不斷被提出，而多分辨率分割(Multiresolution Segmentation)算法的出現，被認為是遙感影像分割的一個里程碑。該算法在影像分割時，綜合了影像的光譜信息和空間信息，能產生內部同質性最高的影像對象，其主要參數有尺度、形狀因子、緊湊度因子，這些參數的不同組合會產生不同的分割結果。選擇質量最好的分割結果的過程被稱為參數優選，而參數優選必須要解決的問題是對分割質量的具體評價。因此，如何獲得最優分割參數組合來評價影像分割質量是OBIA中必須解決的一個問題。

不一致性分割結果評價方法基于參考多邊形(Reference Polygon)和對應的匹配分割多邊形(Corresponding Polygon)之間的不一致性(Discrepancy)來度量當前參數組合所產生的分割數據的質量。它是一種客觀的經驗性評價方法(Empirical Method)，它是用幾何不一致性度量的是參考多邊形與匹配多邊形之間面積的差異，而算術不一致性度量的是兩者多邊形數量的差異。

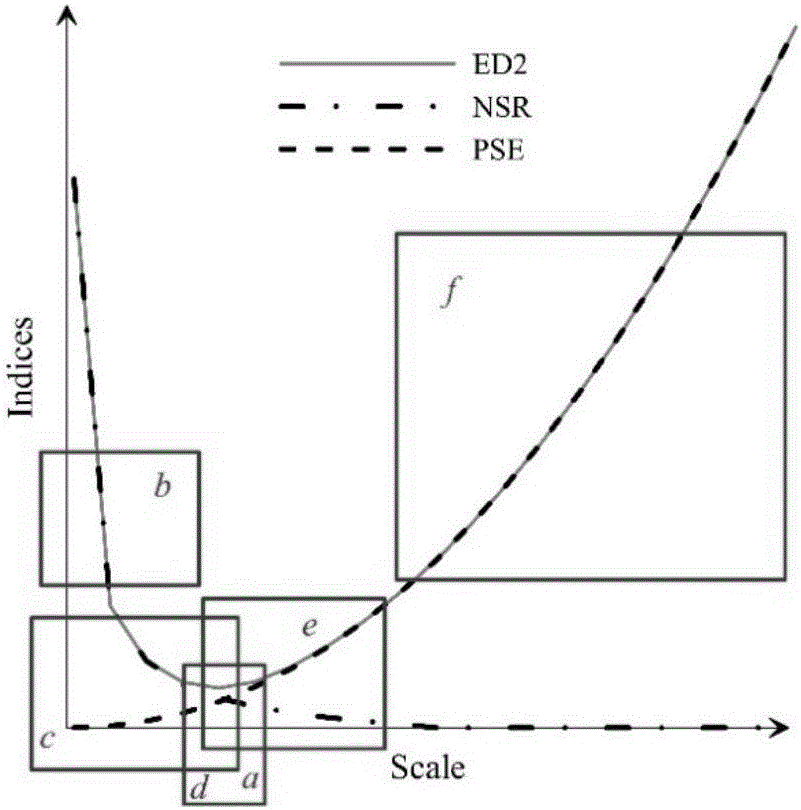
在不一致性評價體系(Potential Segmentation Error,PSE-Number-of-Segments Ratio,NSR-Euclidean Distance 2,ED2)中，PSE是潛在分割誤差面積比，NSR是分割多邊形數量比，ED2是PSE與NSR的歐幾里得距離。斜U型(Euclidean Distance2,ED2-Scale Patterns,SP)模式是基于對PSE-SP,NSR-SP,ED2-SP曲線的分析提出的。在給定形狀、緊湊度參數的情況下，影像分割單元平均面積隨尺度參數的增序近似呈冪函數的形式單調遞增，分割單元的面積隨尺度參數的遞增近似呈冪函數。相應地，分割單元的數量隨尺度參數遞減近似呈冪函數。ED2作為PSE和NSR的組合形式會隨著尺度參數的變化呈現傾斜的U型曲線形式，如圖1所示。

2、現有技術方案

分割質量評價的方法有不一致性法和優度法。基于不一致性評價方法通過比較參考數據集和分割數據集，從幾何不一致性和算術不一致性兩個方面對分割質量進行綜合評價。主要的不一致性評價指標有Clinton等、Weidner等提出的一系列分割質量評價指標QR(Quality Rate)、UR(Under-Segmentation Rate)、OR(Over-Segmentation Rate)和ED1；Liu等基于幾何不一致性和算術不一致性提出了ED2(Euclidean Distance 2)指標；而Yang等通過分析ED1、ED2系列評價指標，進一步提出了ED3、ED3-Modified和SEI(Segmentation Evaluation Index)。同時，Zhang等提出了F-measure指標和MOA(Multiscale Object Accuracy)和BCA(Bidirectional Consistency Accuracy)。基于優度法的分割參數質量評價指標主要是通過局部方差來進行構建的；等(2010)將Kim提出的局部方差評價最優分割尺度的方法進行了自動化，構建了最優尺度參數選取的工具ESP；等(2014)對ESP工具進行了改進。

通過分析和總結最優尺度分割參數選擇方法，提出尺度評定應該結合形狀、紋理等信息，最終實現尺度分割參數的自動選取，然而目前自動化方法多為非監督分割，在一定程度上存在選擇的分割參數尺度偏大，對地物類別的分辨針對性不強，欠分割現象明顯等問題，這會給后續影像分類帶來不利的影響。

技術實現要素：

本發明的目的是克服現有技術的不足，提供了一種基于區域不一致性評價自動優選遙感影像分割參數組合的方法。

本發明的技術方案如下：

本發明公開了一種基于區域不一致性評價自動優選遙感影像分割參數的方法，包括如下步驟：

步驟一：輸入待分割的遙感影像和參考數據集，初始化參數，所述的初始化參數包括給定初始尺度分割參數區間值s₁和s₅，且s₅>s₁，給定尺度分割參數間最小步距d_min，給定ED2_min最大值L、形狀因子、緊湊度因子和ED2_min極小值ζ；

步驟二：如果s₅-s₁>4d_min，則在初始尺度分割參數值s₁和s₅的基礎上設置5個尺度分割參數及其步距，否則需重新設置初始尺度分割參數值s₁和s₅，這里d>d_min為約束條件，s₁，s₂，s₃，s₄，s₅五個尺度分割參數具體計算如下：

s₂＝s₁+d

s₄＝s₅-d

步驟三：根據s₁，s₂，s₃，s₄，s₅尺度分割參數上各自的分割數據集和參考數據集，分別統計其參考多邊形數量、分割多邊形數量，重疊面積、過分割面積、欠分割面積、依次計算出每一個尺度分割參數對應的不一致性度量參數對應的PSE_i，NSR_i和ED2_i，其中i＝{2,3,4,5}。具體計算流程如下：

在每個尺度分割參數中，用R＝{r_i:i＝1,2,...,m}表示m個參考多邊形的集合，S＝{s_j:j＝1,2,...,n}表示分割多邊形的集合，|r_i∩s_j|表示參考多邊形r_i和分割多邊形s_j相交部分的面積，|r_i|和|s_j|分別為參考多邊形r_i和分割多邊形s_j的面積，S'＝{s_k:k＝1,2,...,v}表示與參考數據集相對應的分割數據集的集合。定義Sa和Sb為集合S的兩個子集，且滿足匹配準則：

也就是說匹配準則是參考多邊形和分割多邊形相交部分的面積至少是參考多邊形或匹配多邊形的面積一半，則參考多邊形相匹配的分割多邊形的集合S'就為Sa和Sb的并集。同時定義∑|R_i|為m個參考多邊形的總面積，∑|S_k|為跟m個參考多邊形相匹配的分割多邊形總面積，∑|R_i∩S_k|為參考數據集和匹配的分割數據集重疊面積，|r_i-s_j|＝|r_i|-|r_i∩s_j|是在匹配多邊形之外的那部分參考多邊形的面積為過分割面積，|s_j-r_i|＝|s_j|-|r_i∩s_j|是在參考多邊形之外的那部分匹配多邊形的面積為欠分割面積。因此，PSE、NSR和ED2可以表示為：

最后得到計算5點間的ED2最小值和最大值：

ED2_min＝min{ED2₁,ED2₂,ED2₃,ED2₄,ED2₅}

ED2_max＝max{ED2₁,ED2₂,ED2₃,ED2₄,ED2₅}

步驟四:模式匹配過程

分析ED2隨s₁～s₅尺度分割參數變化的趨勢并動態調整五個尺度分割參數，不斷地匹配PSE-NSR-ED2不一致評價模型Case a～Case q 17種變化模式，獲得在固定形狀因子和緊湊度因子下遙感影像的最優尺度分割參數。

步驟五：依次按照形狀因子＝0.1,0.2,…,0.9，緊湊度因子＝0.1,0.2,…,0.9的組合方式進行步驟一到步驟四的迭代運算，得到81個參數組合上的最優尺度分割參數；然后對這81組最優尺度分割參數進行再排序，從中選出的最小ED2組對應的尺度分割參數，形狀因子及緊湊度因子三個參數組合即為最優分割參數組合。

優選的，所述的步驟四ED2隨尺度分割參數變化的趨勢具有Case a～Case q17種模式：

Case a.ED2_i不隨尺度分割參數發生變化，即ED2₁＝ED2₂＝ED2₃＝ED2₄＝ED2₅，或者其間的最大、最小值之差小于預設的極小值ζ：

|ED2_max-ED2_min|＜ζ

若如此且ED2_max≥L，則意味著預設尺度分割參數明顯偏大至ED2值變化不穩定區域，需要將尺度分割參數范圍向小值方向，將s₅左移到s₁的位置，s₁左移4個步距，s₃為動態調整后s₁和s₅的值一半，s₂和s₄也相應左移4個步距：

s₅←s₁

s₁←s₁-4·d

s₂←s₁+d

s₄←s₅-d

其中“←”表示將箭頭右端的值賦值給箭頭左端的變量，即為尺度分割參數動態調整的過程，五個尺度分割參數的調整是同步進行的，沒有先后之分；箭頭右邊的s1～s5為調整前的尺度分割參數值；以s₅←s₁為例；即表示將原s₁的值賦值給新的s₅，即表示將s₅左移到原s₁的位置。

參數的調整具體是根據尺度分割參數變化的趨勢對s₁～s₅的動態調整，完成相應尺度分割參數“左移”、“右移”、“放大”和“縮小”等，本發明中所有提到的“←”均代表這個意思。

如果s₁<0，則使s₁＝5，s₅左移s₄的位置，d為動態調整后s₁和s₅的值四分之一，s₃為動態調整后s₁和s₅的值二分之一，s₂和s₄左移1個新獲的步距：

s₁←5

s₅←s₄

s₂←s₁+d

s₄←s₅-d

回到步驟三繼續；

否則當滿足條件ED2_max<L時擴大尺度分割參數搜索范圍，相應的s₃不變，s₁減小原來的2倍步距，s₅擴大原來的2倍步距，s₂和s₄分別替換原來的s₁和s₅)

s₂←s₁

s₄←s₅

s₁←s₂-2·d

s₅←s₄+2·d

如果擴大出現s₁<0，則使s₁＝5，s₅左移s₄的位置，d為動態調整后s₁和s₅的值四分之一，s₃為動態調整后s₁和s₅的值二分之一，s₂和s₄左移1個新獲的步距：

s₁←5

s₅←s₄

s₂←s₁+d

s₄←s₅-d

回到步驟三繼續；

如果擴大尺度分割參數范圍搜索，仍出現ED2_i不隨尺度參數發生變化，或其間的最大、最小值之差小于預設的極小值ζ其中之一的情況：

|ED2_max-ED2_min|＜ζ

且ED2_max≤L，則最優尺度分割參數可能位居其一，s_opt∈[s₁,s₅]；需作進一步的判斷：如果前后兩次運算均出現上述狀況，對比前后兩次運算ED_2min，取ED2_min較小的一次作為最優尺度分割參數的范圍，s_opt∈[s₁,s₅]，則s_opt＝s₅，運行結束并報告結果。

Case b.ED2_i隨尺度分割參數的增加而遞減，即ED2₁≥ED2₂≥ED2₃≥ED2₄≥ED2₅，則最優尺度分割參數大于s₅，調整尺度分割參數設置，將s₁右移到s₃的位置，s₂右移到s₄的位置，s₃右移到s₅的位置，s₂和s₄也相應右移2個步距：

s₁←s₃

s₂←s₄

s₃←s₅

s₄←s₃+2·d

s₅←s₄+2·d

回到步驟三繼續；

Case c.ED2_i在s₄處呈現最小值拐點，即ED2₁≥ED2₂≥ED2₃≥ED2₄并且ED2₄≤ED2₅，則最優尺度分割參數可能處于s₃和s₅之間，將尺度分割參數范圍向小值方向，則使s₁右移到s₂的位置，s₂右移到s₃的位置，s₃右移到s₄的位置，s₄右移到s₅的位置，s₅右移1個步距：

s₁←s₂

s₂←s₃

s₃←s₄

s₄←s₅

s₅←s₄+d

回到步驟三繼續；

Case d.ED2_i在s₃處呈現最小值拐點，即ED2₁≥ED2₂≥ED2₃，并且ED2₃≤ED2₄≤ED2₅，則最優尺度分割參數處于s₂和s₄之間；進而如果ED2₃≥L，則意味著預設尺度分割參數明顯偏大至ED2值變化不穩定區域，需要將尺度分割范圍向小值方向，將s₅左移到s₁的位置，s₁左移4個步距，s₃為動態調整后s₅和s₁的二分之一，s₂和s₄也相應左移4個步距：

s₅←s₁

s₁←s₁-4·d

s₂←s₁+d

s₄←s₂-d

如果s1<0，則使s₁＝5，s₅左移s₄的位置，d為動態調整后s₁和s₅的值四分之一，s₃為動態調整后s₁和s₅的值二分之一，s₂和s₄也相應左移1個新獲的步距：

s₁←5

s₅←s₄

s₂←s₁+d

s₄←s₅-d

回到步驟三繼續；

否則ED2₃<L，并且d＞d_min，則需要在s₂和s₄之間加密搜索，相應的s₃不變，將s₁左移到s₂的位置，s₅左移到s₄的位置，s₂和s₄也相應左移二分之一個步距：

s₁←s₂

s₅←s₄

直到d≤d_min，且滿足ED2₃<L，則s_opt＝s₃。

Case e.ED2_i在s₂處呈現最小值拐點，即ED2₁≥ED2₂，并且ED2₂≤ED2₃≤ED2₄≤ED2₄，則最優尺度分割參數可能處于s₁和s₃之間，若ED2₂<L，且d<d_min，則s₂為最優參數；否則如果ED2₂≥L，則需要將尺度分割參數范圍向小值方向，則使s₅左移到s₄的位置，s₄左移到s₃的位置，s₃左移到s₂的位置，s₂左移到s₁的位置，s₁左移1個步距：

s₅←s₄

s₄←s₃

s₃←s₂

s₂←s₁

s₁←s₁-d

如果s₁<0，則使s₁＝5，s₅左移s₄的位置，d為動態調整后s₁和s₅的值四分之一，s₃為動態調整后s₁和s₅的值二分之一，s₂和s₄也相應左移1個新獲的步距：

s₁←5

s₅←s₄

s₂←s₁+d

s₄←s₅-d

回到步驟三繼續；

否則當ED2₂<L，且d>d_min，在s₁和s₃處加密，則需要在s₂和s₄之間加密搜索，相應的s₃不變，將s₁左移到s₂的位置，s₅左移到s₄的位置，s₂和s₄也相應左移二分之一個步距：

s₁←s₂

s₅←s₄

回到步驟三繼續；

Case f.ED2_i隨尺度分割參數遞增，即ED2₁≤ED2₂≤ED2₃≤ED2₄≤ED2₂，則最優尺度分割參數小于s₁或者鄰近s₁，則使s₅左移到s₃的位置，s₃左移到s₁的位置，s₄左移到s₂的位置，s₂左移2個步距，s₁左移2個步距：

s₅←s₃

s₃←s₁

s₄←s₂

s₂←s₃-d

s₁←s₂-d

如果s₁<0，則使s₁＝5，s₅左移s₄的位置，d為動態調整后s₁和s₅的值四分之一，s₃為動態調整后s₁和s₅的值二分之一，s₂和s₄也相應左移1個新獲的步距：

s₁←5

s₅←s₄

s₂←s₁+d

s₄←s₅-d

回到步驟三繼續；

Case g-Case q.隨尺度分割參數遞增，ED2_i隨尺度分割參數的變化趨勢趨于不穩定，ED2i值隨尺度分割參數變化而至不穩定區域，且ED2_min≥L，則意味著預設尺度分割參數明顯偏大至ED2_i值變化不穩定區域，需要將分割尺度參數范圍向小值方向左移，將s₅左移到s₁的位置，s₁左移4個步距，s₃為動態調整后s₁和s₅的值一半，s₂和s₄也相應左移4個步距：

s₅←s₁

s₁←s₁-4·d

s₂←s₁+d

s₄←s₂-d

如果s₁<0，則使s₁＝5，s₅左移s₄的位置，d為動態調整后s₁和s₅的值四分之一，s₃為動態調整后s₁和s₅的值二分之一，s₂和s₄也相應左移1個新獲步距：

s₁←5

s₅←s₄

s₂←s₁+d

s₄←s₅-d

回到步驟三繼續:否則遇到ED2_max≤L時，將放大后計算獲得的這組數據與上一組數據的ED2_min進行比較，如果出現小于上一組最小值的情況就繼續放大，直到找到最小的ED2_min，放大結束，確定最小ED2_min的區間，然后在最小區間進行加密，加密到d≤d_min，加密結束，取其ED2_min對應的尺度分割參數為最優尺度分割參數。

優選的，所述的步驟一中給定尺度分割參數間最小步距d_min＝1，給定ED2_min最大值L＝1.0、形狀因子＝0.1、緊湊度因子＝0.1、ED2_min極小值ζ＝0.0001。

本發明將地學空間分析和模式匹配用到具體問題上，確定的最優分割參數可用地學空間分析以及基于幾何不一致性和算術不一致性原理明確地加以解釋，具有更高的理論可信度。

本發明方法，不拘泥于遙感影像分割參數優選算法，可以廣泛應用于任何服從斜U型曲線分布的模型求最優值的問題，該方法具有廣泛的實用性和應用價值。

本發明方法，實質上是遙感影像分析之前分割參數的預測，避免了選擇參數的盲目性，解決了試錯法帶來的不確定性和窮舉法帶來的耗時，兼顧了工作效率的同時，也提高了面向對象遙感影像處理與分析的精度和自動化程度。

附圖說明

圖1為給定形狀因子和緊湊度因子下斜U型ED2-SP模式示意圖；

圖2為ED2隨尺度分割參數變化的17種基本模式示意圖；

圖3為本發明實施例的基于區域不一致性評價自動優選遙感影像分割參數的方法流程流程圖；

圖4為本發明實施例與窮舉法選擇遙感影像最優分割參數組合自動搜索的軌跡對比圖；

圖5為本發明實施例應用在廣東省東莞市Quick bird高分辨率遙感影像中的分割效果圖；

圖6為本發明實施例應用在寧夏回族自治州中衛市World view2高分辨率遙感影像中的分割效果圖。

具體實施方式

如圖3所示，為本發明實施例的基于區域不一致性評價自動優選遙感影像分割參數的方法流程流程圖；在本發明的所有實施例中，步驟一給定尺度分割參數間最小步距d_min＝1，給定ED2_min最大值L＝1.0、形狀因子＝0.1、緊湊度因子＝0.1、ED2_min極小值ζ＝0.0001。

如圖2所示為ED2隨尺度分割參數變化的17種基本模式示意圖。

1.本發明的方法與窮舉法選擇最優分割參數組合的對比

將本發明實施例應用到廣東省東莞市和寧夏回族自治州中衛市三種傳感器(Quick bird、Alos、World view2)多光譜和融合的6景高分辨率遙感影像中3種不同地物(耕地FL、居民住宅RB、坑塘WB)最優分割參數組合的選擇，并與窮舉法獲得的結果進行比較，實驗中用相同配置的計算機進行測試，將初始尺度參數范圍進行統一，確保兩種方法具有可比性，獲得實驗結果，其中窮舉法實驗結果如表1所示，本發明的方法結果如表2所示。

對比表1和表2，可以發現本發明實施例在相同的初始尺度參數范圍下，基本都能產生較小數據量級的分割數據集，所耗費時間也相對也較短，且可以將步長精確到1，獲得更加精確的ED2的取值來確定遙感影像的最優分割參數組合，然而目前流行的窮舉法需要機械地產生步長規定的分割數據集，步長一旦確定也不能動態調整，找到的初始尺度參數范圍，也會因為初始尺度參數范圍考慮不全面，沒有列舉到最優分割參數組合存在的范圍，給尋找參數帶來了具體的制約性。通過這個實驗的對比，本發明實施例表現良好，不但可以通過設置合適的初始尺度參數范圍快速的得到最優尺度分割參數，而且可以動態改變步長，可以精準預測PSE‐NSR‐ED2不一致性評價模型取得最優尺度分割參數的區間，節約時間的同時避免了選擇最優分割參數組合的盲目性。

表1窮舉法結果統計表

表2本發明方法結果統計表

從表1和表2獲得大量的數據中抽取一組形狀因子和緊湊度因子都為0.1時，選擇最優尺度分割參數的軌跡進行分析，可以清楚的看到本發明實施例中可以在初始尺度分割參數的范圍內快速預測到最優尺度分割參數的存在的區間，然后開始加密確定最優，而窮舉法沒有任何搜索軌跡，需要人工判斷斜U型曲線最優的位置，如圖4所示。

2.本發明的方法與其他自動化分割參數優選工具對比

將本發明實施例與等(2014)提出的自動優選遙感影像尺度參數的工具ESP進行對比，實驗數據為廣東省東莞市和寧夏回族自治州中衛市三種傳感器(Quick bird、Alos、World view2)3景高分辨率遙感影像中3種不同地物(耕地、林地、坑塘)，由于ESP只能選擇最優尺度分割參數，將本發明實施例中找到的形狀因子和緊湊度因子作為標準，并設置相同的初始尺度參數和步長進行對比實驗。根據分割精度評價指標中的規定，生產者精度和用戶精度都接近1，分割效果最優的原則衡量表3中的結果，可以發現ESP工具的用戶精度很不穩定，最低達到0.11，而且找到的最優尺度分割參數明顯偏大，分割數據集量級很大，整體效率較差。

表3最優分割參數結果及精度評價對比統計表

3.圖5為本發明實施例和窮舉法獲得的最優分割參數組合對廣東省東莞市Quick bird高分辨率遙感影像對水體的分割效果，可以看出已經能很好的劃分水體的區域，過分割和欠分割現象都解決良好；圖6為本發明實施例和窮舉法獲得的最優分割參數組合對寧夏回族自治州中衛市World view2高分辨率遙感影像對耕地的分割效果,，明顯可以看出本發明實施例已經可以預測出此類地物的最優尺度分割參數范圍比較大，但是窮舉法已經盲目認為初始尺度參數范圍已經估計到了最大范圍，這樣人工的判讀存在嚴重的主觀性。