本發明屬于數據處理技術領域，具體而言，涉及一種用于管網建模的時序數據清洗方法。

背景技術：

管網建模過程中涉及到大量監測數據處理，例如涉及到的以時間序列的數據主要有水廠出水壓力和出水流量的監測數據，居民生活用水量、用水模式數據，用于模型校驗的管網監測點的壓力、流量數據等。但是，這些數據中有些是正確的，而有些則由于機械儀器誤差等某些不特定因素，會不可避免的存在某些時間點異常值、數據缺失、數據重復等問題。如果不加以篩選，勢必會對模型計算結果產生一定的影響甚至有可能直接導致模型計算不收斂，模型崩潰等現象的發生，因此我們在將這些數據導入到模型計算之前需進行數據的預處理使之達到清洗的效果，為模型的計算提供保證。

例如，在收集到的時序監測數據中，有時候會出現個別的異常數值，從直觀上看，這個數據要比其它數據小許多或者大很多。在處理試驗數據時，對于這樣的個別異常值，是否要剔除，剔除后如何補齊，如果單純憑直覺判斷，缺乏理論上的依據。對于建模監測數據中上述異常值、數據缺失、數據重復問題，目前還沒有一套完整的標準化處理流程。通常在建模時對于異常值僅為人工判斷合理區間，對于缺失值和異常值的處理是忽略缺失值使用簡單的線性差值來補充異常值。

技術實現要素：

本發明的目的在于提供一種用于管網建模的時序數據清洗方法，該方法針對管網建模中的時序數據，能夠采取較為合理科學的數據預處理方式為模型計算的精度提供保證。

為實現上述技術目的，達到上述技術效果，本發明通過以下技術方案實現：

一種用于管網建模的時序數據清洗方法，包括以下步驟：

步驟1）重復值篩出；

利用結構化查詢語言（SQL）選取所需時間段的數據，同一監測點位的數據作為一組，進行重復值查找，并刪除相同時間點的重復值；

步驟2）離散程度分析；

批量分別計算不同組數據最大值X_max、最小值X_min、平均值μ、標準差σ和變異系數CV，其中CV=σ/μ，通過標準差σ和變異系數CV來分析數據的離散程度，通過變異系數CV的處理可將不同量綱的流量和壓力數據同一批次處理；并對變異系數CV設定閾值，當變異系數大于所設定的閾值時，則判定該監測點位的數據為無效數據，并進行刪除，不參與模型計算；

步驟3）異常值判定；

通過三倍標準差法確定上下限值，即正常值X為，確定上限值為，確定下限值為，對于不符合此范圍的值均為異常值進行剔除；

步驟4）平滑曲線去噪點；

對于已去除異常值的各組監測點（離散點）數據采用最小二乘法擬合平滑曲線，首先確定一個函數逼近原函數；設近似函數為，函數值與觀測值之差稱為殘差，可以用殘差來衡量近似函數的好壞，具體方法為：

根據已知數據點，先利用MATLAB解方程組，得到待定系數和擬合函數；再利用擬合函數值代替曲線噪點值，達到曲線平滑的效果；進一步的，可將替換噪點值后擬合函數值再次進行擬合，重復上述步驟直至殘差滿足精度要求；

步驟5）對缺失值進行插值處理；

采用三次樣條函數對缺失值進行插值，通過上述步驟描述處理監測的時序數據重復值、缺失值、異常值以及離散度較大的序列數據；

在實際建模過程中進行數據處理時，先通過最小二乘法擬合出最逼近觀測值的函數，總體把握數據的趨勢走向，同時甄別步驟3）中未能通過三倍標準差發去除的異常值并剔除，減小誤差的存在；

在實際導入模型數據時，再利用局部分段的數據，采用三次樣條曲線插值法將缺失值及異常值剔除的部分進行補齊，以防止擬合曲線數據的失真，同時保留了原合理的觀測值。

進一步的，步驟1）中，所述的時間段數據包括水廠出水壓力和出水流量的監測數據，居民生活用水量、用水模式數據，以及用于模型校驗的不同管網監測點位的壓力、流量時序數據。

進一步的，步驟2）中，所述變異系數的閾值可設定為1，即標準差σ小于平均值μ，實踐中當變異系數＜1時，所監測的壓力和流量時序列數據離散程度較好。

進一步的，在步驟4）中，所述的函數的曲線在曲線圖上不要求過所有的數據點（可以消除誤差影響），但需要盡可能表現出數據的趨勢，靠近這些數據點即可。

本發明的有益效果是：

本發明提供了異常值的判定，不同量綱的壓力數據流量數據的標準化處理，采用差異顯著性分析對異常值快速查找及替換的方法，同時對缺失數據進行比較后選擇最合理的插值方式等一整套的數據處理流程。通過引入變異系數（標準差/平均數）以實現不同量綱的壓力數據和流量數據標準化處理，可以同時進行判定數組的離散程度并篩選。本發明在方法上先用三倍標準差法對于異常值數據查找處理再用最小二乘法擬合，極大減小了異常值對擬合結果的影響；同時用擬合函數對噪點數據平滑處理進一步的減少異常數據的存在，最小二乘法擬合能夠滿足不符合正態分布的數據處理；最后采用三次樣條插值較線性插值能夠使插入的數值更加平滑。因此本發明的方法能夠在將數據導入到模型計算之前對其進行預處理，以達到數據清洗的效果，為模型的計算提供保證。

上述說明僅是本發明技術方案的概述，為了能夠更清楚了解本發明的技術手段，并可依照說明書的內容予以實施，以下以本發明的較佳實施例并配合附圖詳細說明如后。本發明的具體實施方式由以下實施例及其附圖詳細給出。

附圖說明

此處所說明的附圖用來提供對本發明的進一步理解，構成本申請的一部分，本發明的示意性實施例及其說明用于解釋本發明，并不構成對本發明的不當限定。在附圖中：

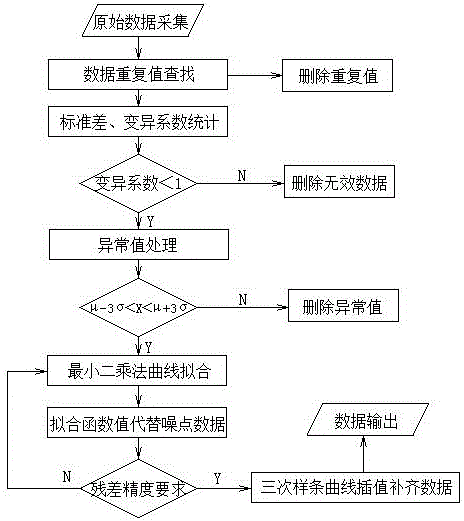
圖1為本發明的時序數據清洗方法的流程圖。

具體實施方式

下面將參考附圖并結合實施例，來詳細說明本發明。

參照圖1所示，一種用于管網建模的時序數據清洗方法，包括以下步驟：

步驟1）重復值篩出

利用結構化查詢語言（SQL）選取所需時間段的數據，所述的時間段數據包括水廠出水壓力和出水流量的監測數據，居民生活用水量、用水模式數據，以及用于模型校驗的不同管網監測點位的壓力、流量時序數據；同一監測點位的數據作為一組，進行重復值查找，并刪除相同時間點的重復值。

步驟2）離散程度分析

批量分別計算不同組數據最大值Xmax、最小值Xmin、平均值μ、標準差σ和變異系數CV。

設這組數值X₁，X₂，X₃，......X_n其平均值（算術平均值）為μ；則標準差σ為：

變異系數為：CV=σ/μ。

通過標準差σ和變異系數CV來分析數據的離散程度，通過變異系數CV的處理可將不同量綱的流量和壓力數據同一批次處理；并對變異系數CV設定閾值，當變異系數大于所設定的閾值時，則判定該監測點位的數據為無效數據，并進行刪除，不參與模型計算。

實際建模中通常會有某監測點位部分時間段采集到的數據均為0，其余時間點數據正常，與實際情況并不符合，此組數據為無效數據，這樣的數據的標準差及變異系數較大，因此可以通過離散度來分析去除。

實際經驗中當變異系數＜1時，所監測的數據離散程度較好，對于建模中所監測的流量和壓力時序數據的變異系數的閾值可選擇為1，即標準差σ小于平均值μ。

步驟3）異常值判定

通過三倍標準差法確定上下限值，即正常值X為，確定上限值為，確定下限值為，對于不符合此范圍的值均為異常值進行剔除。對于符合正態分布的數據數值分布在（μ-3σ，μ+3σ）中的概率為0.9974，因此在該區間之外的數據均被認為是異常值。

步驟4）平滑曲線去噪點；

對于已去除異常值的各組監測點（離散點）數據采用最小二乘法擬合平滑曲線，首先確定一個函數逼近原函數，該函數的曲線在曲線圖上不要求過所有的數據點（可以消除誤差影響），但該函數需要盡可能表現出數據的趨勢，靠近這些數據點。

設近似函數為，函數值與觀測值之差稱為殘差，可以用殘差來衡量近似函數的好壞，具體實現方法如下：

設已知數據點，求m次多項式來擬合函數。需要求出m+1項多項式的待定系數即可，且使得以下函數值達到最小：

；

要使上述函數達到最小值，由高等數學知識有：

；

即

；

于是得到法方程：

；

轉換成矩陣如下

；

利用MATLAB解方程組，得到待定系數和擬合函數。

利用擬合函數值代替曲線噪點值，達到曲線平滑的效果。進一步可將噪點值替換后再次進行擬合，重復上述步驟直至殘差滿足精度要求。

步驟5）對缺失值進行插值處理

采用三次樣條函數對缺失值進行插值，通過上述步驟描述處理監測的時序數據重復值、缺失值、異常值以及離散度較大的序列數據；

在實際建模過程中進行數據處理時，先通過最小二乘法擬合出最逼近觀測值的函數，總體把握數據的趨勢走向，同時甄別步驟3）中未能通過三倍標準差發去除的異常值并剔除，減小誤差的存在；

在實際導入模型數據時，再利用局部分段的數據，采用三次樣條曲線插值法將缺失值及異常值剔除的部分進行補齊，具體實現方法如下：

在[a,b]上函數的三次樣條插值函數S(x)滿足：

（1）在[a,b]上0,1,2介導數連續，即

；

（2）；

（3）在區間上是三次多項式。

通過上述插值處理對剔除的異常值及缺失值進行補齊，以防止擬合曲線數據的失真，同時保留了原合理的觀測值。

以上所述僅為本發明的優選實施例而已，并不用于限制本發明，對于本領域的技術人員來說，本發明可以有各種更改和變化。凡在本發明的精神和原則之內，所作的任何修改、等同替換、改進等，均應包含在本發明的保護范圍之內。