本發(fā)明是一種考慮振幅約束的Halo軌道在軌保持方法，適用于真實(shí)星歷環(huán)境并考慮測(cè)量與執(zhí)行誤差條件下的平衡點(diǎn)Halo軌道在軌保持控制，屬于航空航天技術(shù)領(lǐng)域。

背景技術(shù)：

平衡點(diǎn)是探測(cè)器和兩個(gè)相互環(huán)繞的主天體構(gòu)成的三體系統(tǒng)中具有特殊性質(zhì)的點(diǎn)，位于平衡點(diǎn)的物體相對(duì)主天體可以保持相對(duì)靜止。平衡點(diǎn)附近存在滿足一定速度位置約束的圍繞平衡點(diǎn)運(yùn)動(dòng)的周期軌道，位于周期軌道上的物體同樣相對(duì)大、小質(zhì)量天體保持基本不變的位置關(guān)系。同時(shí)相比將探測(cè)器捕獲至環(huán)繞軌道，捕獲至平衡點(diǎn)周期軌道所需的速度增量相對(duì)較小。因此，以Halo軌道為代表的平衡點(diǎn)周期軌道非常適合行星探測(cè)和中繼通訊任務(wù)，是未來(lái)探測(cè)器的理想工作地點(diǎn)。而在真實(shí)星歷環(huán)境下探測(cè)器會(huì)受到其他天體的引力擾動(dòng)，因此探測(cè)器在Halo軌道每隔一段時(shí)間需要進(jìn)行在軌保持修正。

在已發(fā)展的關(guān)于Halo軌道在軌保持方法中在先技術(shù)[1](參見(jiàn)Howell K C,Pernicka H J.Station-keeping method for libration point trajectories[J].Journal of Guidance Control&Dynamics,1990,16(1):713-723.)給出了一種平衡點(diǎn)軌道在軌保持方法，該方法借鑒了行星際多目標(biāo)探測(cè)轉(zhuǎn)移軌道中途修正的計(jì)算方法，先根據(jù)任務(wù)需求將軌道分為多個(gè)轉(zhuǎn)移段，再通過(guò)微分修正算法將轉(zhuǎn)移軌道修正到標(biāo)稱節(jié)點(diǎn)上，從而得到每次變軌所需的最優(yōu)速度增量。該方法雖然可以實(shí)現(xiàn)平衡點(diǎn)周期軌道的在軌保持，但每次軌道修正計(jì)算都需要標(biāo)稱軌道節(jié)點(diǎn)，因此該方法對(duì)于Halo軌道長(zhǎng)期在軌保持存在較大的不便。

在先技術(shù)[2](參見(jiàn)Ulybyshev Y.Long-Term Station Keeping of Space Station in Lunar Halo Orbits[J].Journal of Guidance Control&Dynamics,2015,38(6).)給出了另一種Halo軌道長(zhǎng)期在軌保持方法，該方法不需要在修正時(shí)得到標(biāo)稱軌道節(jié)點(diǎn)，只需保證在旋轉(zhuǎn)坐標(biāo)系下軌道每次穿過(guò)X-Z平面時(shí)X方向的速度為零。該方法得到的速度增量較小，計(jì)算簡(jiǎn)單，但隨著在軌保持時(shí)間增長(zhǎng)，Halo軌道的振幅會(huì)發(fā)生較大的改變。

技術(shù)實(shí)現(xiàn)要素：

本發(fā)明的目的是為了提供一種考慮振幅約束的一種Halo軌道在軌保持方法。該方法基于真實(shí)星歷模型，同時(shí)考慮探測(cè)器的測(cè)量誤差和執(zhí)行誤差，在實(shí)現(xiàn)滿足振幅約束的Halo軌道在軌保持前提下盡可能降低軌道保持所需的燃料消耗。

本發(fā)明的目的是通過(guò)下述技術(shù)方案實(shí)現(xiàn)的。

考慮振幅約束的一種Halo軌道在軌保持方法，通過(guò)在兩個(gè)主天體和探測(cè)器構(gòu)成的限制性三體模型下建立動(dòng)力學(xué)方程，確定兩個(gè)主天體和探測(cè)器構(gòu)成的三體系統(tǒng)平衡點(diǎn)位置。確定大小天體和探測(cè)器構(gòu)成的三體系統(tǒng)下平衡點(diǎn)附近的Halo軌道。根據(jù)擾動(dòng)變量設(shè)計(jì)Halo軌道保持的微分修正算法。根據(jù)微分修正算法設(shè)計(jì)Halo軌道在軌保持策略。在真實(shí)星歷環(huán)境下，考慮測(cè)量誤差和執(zhí)行誤差，按照所述的軌道保持策略采用微分修正算法得到每次軌道修正的速度增量，按照速度增量進(jìn)行軌道修正控制，可以實(shí)現(xiàn)滿足振幅約束的Halo軌道在軌保持，同時(shí)盡可能降低軌道保持所需的燃料消耗。

考慮振幅約束的一種Halo軌道在軌保持方法，包括如下步驟：

步驟一：在兩個(gè)主天體和探測(cè)器構(gòu)成的限制性三體模型下建立動(dòng)力學(xué)方程，確定兩個(gè)主天體和探測(cè)器構(gòu)成的三體系統(tǒng)平衡點(diǎn)位置。

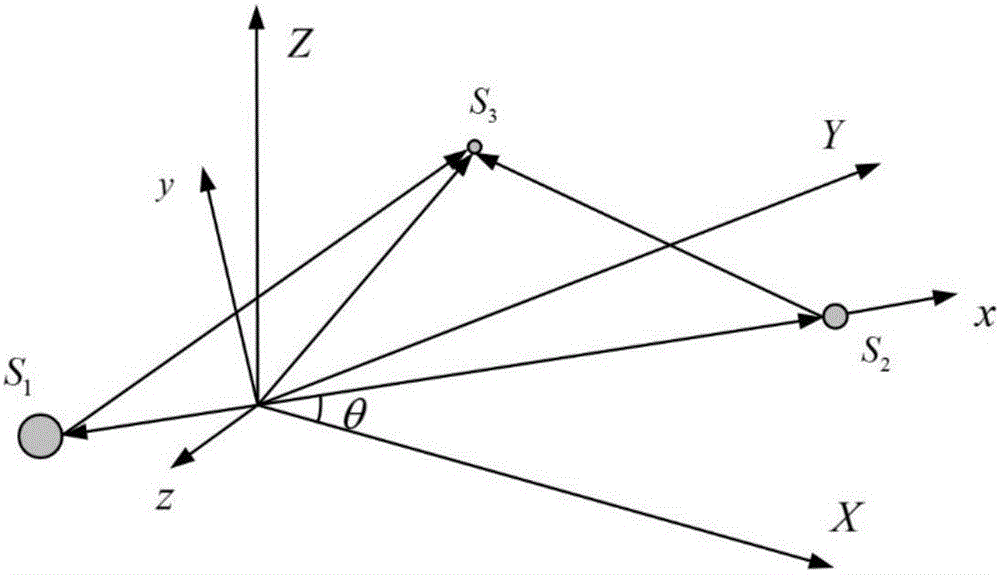
限制性三體模型動(dòng)力學(xué)系統(tǒng)中考慮質(zhì)量可以忽略的探測(cè)器S₃在兩個(gè)主天體S₁和S₂的引力共同作用下的運(yùn)動(dòng)，兩個(gè)主天體S₁、S₂和探測(cè)器S₃三者質(zhì)量關(guān)系為m₁＞m₂＞＞m₃。選擇兩個(gè)主天體系統(tǒng)的質(zhì)心作為原點(diǎn)建立旋轉(zhuǎn)坐標(biāo)系，x軸方向由原點(diǎn)指向小天體，z軸為系統(tǒng)旋轉(zhuǎn)的角速度方向，y軸與x、z軸構(gòu)成右手坐標(biāo)系。則探測(cè)器的運(yùn)動(dòng)描述為式(1)：

其中μ＝m₂/(m₁+m₂)表示系統(tǒng)的質(zhì)量系數(shù)，m₁為較大主天體S₁的質(zhì)量，m₂為較小主天體S₂的質(zhì)量，分別為運(yùn)動(dòng)探測(cè)器到兩主天體的距離。

為獲得旋轉(zhuǎn)坐標(biāo)系平衡點(diǎn)，令式(1)中速度和加速度等于0，共可獲得五個(gè)平衡點(diǎn)(拉格朗日點(diǎn))；所述五個(gè)平衡點(diǎn)均在x-y平面上，包括三個(gè)共線的平衡點(diǎn)和兩個(gè)三角平衡點(diǎn)。在質(zhì)心旋轉(zhuǎn)系下三個(gè)共線平衡點(diǎn)的位置(x_Li,y_Li)分別為：

L1平衡點(diǎn)：L2平衡點(diǎn)：L3平衡點(diǎn)：

兩個(gè)三角平衡點(diǎn)的位置分別為：

L4平衡點(diǎn)：L5平衡點(diǎn)：

步驟二：確定大主天體、小主天體和探測(cè)器構(gòu)成的三體系統(tǒng)下平衡點(diǎn)附近的Halo軌道。

為獲得更簡(jiǎn)潔的表達(dá)式，引入變量(ξ,η,ζ)，根據(jù)步驟一所得的平衡點(diǎn)的位置對(duì)旋轉(zhuǎn)坐標(biāo)系坐標(biāo)進(jìn)行替換，變量定義如下：

ξ＝x-x_Li；η＝y(tǒng)-y_Li；ζ＝z

平衡點(diǎn)附近的線性化運(yùn)動(dòng)方程可描述為式(2)：

式(2)中，ρ²＝x²+y²+z²；c₂(μ)、c_n(μ)為僅與質(zhì)量有關(guān)的常數(shù)，可表示為式(3)：

式(3)中，γ為平衡點(diǎn)與主天體S₂的距離，p_n為n階Legendre多項(xiàng)式。對(duì)方程(2)進(jìn)行分析，平衡點(diǎn)附近Halo軌道線性項(xiàng)可表示為式(4)：

式(4)中，ω₀分別為周期軌道運(yùn)動(dòng)的頻率，κ為常數(shù)，φ為Halo軌道相位；α、β分別為軌道平面和垂直振幅；但為了滿足Halo軌道的周期性，要求平衡點(diǎn)附近Halo軌道的非線性項(xiàng)可表示為式(5)：

式(5)中，θ＝ω₀t+φ，i+j＝N稱為解的階數(shù)。利用式(4)和(5)作為平衡點(diǎn)附近Halo軌道的初值，通過(guò)多重打靶方法可以得到Halo軌道的精確數(shù)值解，即三體系統(tǒng)下平衡點(diǎn)附近的Halo軌道。

步驟三：根據(jù)擾動(dòng)變量設(shè)計(jì)Halo軌道保持的微分修正算法；根據(jù)微分修正算法得到Halo軌道精確數(shù)值解。

引入擾動(dòng)變量，相對(duì)于參考軌道的變分為(δx,δy,δz)，則六維狀態(tài)矢量為：

則變分方程的狀態(tài)空間形式表示為方程(6)：

與時(shí)間有關(guān)的矩陣A(t)是由4個(gè)3×3的矩陣構(gòu)成，即式(7)：

式(7)中B(t)是一個(gè)時(shí)變函數(shù)，因此A(t)也是一個(gè)時(shí)變函數(shù)，I₃是3×3的單位矩陣，C為常值矩陣，滿足如下表達(dá)式：

方程(6)的解的形式為式(8)：

這里Φ(t,t₀)是狀態(tài)轉(zhuǎn)移矩陣。狀態(tài)轉(zhuǎn)移矩陣是從初始狀態(tài)到t時(shí)刻狀態(tài)的線性映射，通過(guò)狀態(tài)轉(zhuǎn)移矩陣可估算出初始狀態(tài)變分對(duì)軌道遞推的影響。狀態(tài)轉(zhuǎn)移矩陣必須滿足矩陣微分方程(9)：

方程(9)的初始條件為Φ(t₀,t₀)＝I₆，這里I₆為6×6的單位陣。在t時(shí)刻的單位狀態(tài)轉(zhuǎn)移矩陣，通過(guò)初始條件的數(shù)值積分得到。因?yàn)闋顟B(tài)轉(zhuǎn)移矩陣是6×6，所以方程(9)的遞推可以通過(guò)36個(gè)一階微分方程的積分得到。B(t)的元素取決于參考軌道，因此求解A(t)，方程(9)需要同時(shí)積分非線性方程，從而得到狀態(tài)轉(zhuǎn)移矩陣Φ(t,t₀)。

根據(jù)微分修正算法求解Halo軌道精確數(shù)值解一般需要通過(guò)多次迭代過(guò)程來(lái)完成，歸結(jié)如下：

根據(jù)當(dāng)前末端狀態(tài)與理想狀態(tài)的偏差，通過(guò)狀態(tài)轉(zhuǎn)移矩陣對(duì)初始狀態(tài)進(jìn)行修正，使得最終的末端狀態(tài)滿足要求的約束條件。選取六維狀態(tài)矢量尋找初始狀態(tài)使周期軌道在t_f時(shí)刻滿足約束條件末端狀態(tài)偏差與初始狀態(tài)偏差的關(guān)系為式(10)：

矩陣的偏導(dǎo)數(shù)等于在t_f時(shí)刻的狀態(tài)轉(zhuǎn)移矩陣，那么方程(8)可以簡(jiǎn)化為方程(11)：

末端狀態(tài)的偏差量為方程(12)：

為目標(biāo)終端狀態(tài)，為實(shí)際終端狀態(tài)，將方程(12)代入方程(11)，可以解出一個(gè)初始狀態(tài)修正量的估計(jì)值

由于Halo軌道關(guān)于x-z平面對(duì)稱，周期軌道必定與x-z平面垂直，因此在交叉處有滿足式(13)：

利用垂直平面相交的特點(diǎn)進(jìn)一步對(duì)問(wèn)題進(jìn)行簡(jiǎn)化，為了滿足Halo軌道在半個(gè)周期后滿足垂直交叉的條件則需選擇y_f＝0作為積分終止的條件，在利用方程(11)迭代過(guò)程中需要調(diào)整初始狀態(tài)使得末端的狀態(tài)和接近于0，從而得到三維周期Halo軌道的精確數(shù)值解。

步驟四：根據(jù)步驟三中的微分修正算法設(shè)計(jì)Halo軌道的在軌保持策略。

由步驟三可知理想Halo軌道保持需要滿足垂直交叉條件，即滿足但在真實(shí)星歷環(huán)境下，嚴(yán)格滿足約束的Halo軌道是不存在的，只需保證Halo軌道的振幅尺寸滿足規(guī)定的范圍即可。因此對(duì)于Halo軌道的在軌保持修正，可以不嚴(yán)格滿足約束條件針對(duì)修正約束條件的嚴(yán)格性提出兩種不同的修正策略：寬松修正方法和嚴(yán)格修正方法。

寬松修正方法是指：軌道積分穿過(guò)x-z平面時(shí)x方向的速度為零，即嚴(yán)格修正方法是指：軌道積分穿過(guò)x-z平面時(shí)x方向和z方向的速度均為零，也即

當(dāng)軌道穿過(guò)x-z平面時(shí)z方向的振幅超過(guò)任務(wù)約束的任務(wù)上下邊界時(shí)執(zhí)行一次嚴(yán)格修正方法，否則執(zhí)行寬松修正方法。同時(shí)在每?jī)蓚€(gè)軌道周期內(nèi)執(zhí)行的4次修正中至少執(zhí)行1次嚴(yán)格修正策略。

步驟五：在真實(shí)星歷環(huán)境下，考慮測(cè)量誤差和執(zhí)行誤差，采用步驟四中的在軌保持策略進(jìn)行Halo軌道在軌保持。

軌道保持修正采用步驟三中的微分修正算法。在求解修正脈沖時(shí)，積分初值為考慮測(cè)量誤差的實(shí)際狀態(tài)；而在軌道修正時(shí)，需要在實(shí)際狀態(tài)進(jìn)行脈沖修正時(shí)考慮修正的執(zhí)行誤差。在考慮測(cè)量誤差和執(zhí)行誤差的條件下，按照軌道保持策略采用微分修正算法得到每次軌道修正的速度增量，按照速度增量進(jìn)行軌道修正控制可以實(shí)現(xiàn)滿足振幅約束的Halo軌道在軌保持，同時(shí)盡可能降低軌道保持所需的燃料消耗。

有益效果

1、本發(fā)明公開(kāi)的考慮振幅約束的一種Halo軌道在軌保持方法，該方法不需要在修正時(shí)得到標(biāo)稱軌道節(jié)點(diǎn)，計(jì)算簡(jiǎn)單，適合探測(cè)器在Halo軌道的長(zhǎng)期在軌保持。

2、本發(fā)明公開(kāi)的考慮振幅約束的一種Halo軌道在軌保持方法，該方法根據(jù)兩種不同修正策略的各自優(yōu)勢(shì)，設(shè)計(jì)了一種組合修正策略，可以實(shí)現(xiàn)滿足振幅約束的Halo軌道在軌保持，同時(shí)盡可能降低軌道保持所需的燃料消耗。

3、本發(fā)明公開(kāi)的考慮振幅約束的一種Halo軌道在軌保持方法，該方法基于真實(shí)星歷模型，考慮探測(cè)器的測(cè)量誤差和執(zhí)行誤差，Halo軌道在軌保持更加接近工程應(yīng)用環(huán)境。

附圖說(shuō)明：

圖1本發(fā)明方案流程示意圖。

圖2限制性三體模型旋轉(zhuǎn)坐標(biāo)系示意圖。

圖3限制性三體系統(tǒng)平衡點(diǎn)分布示意圖。

圖4本發(fā)明實(shí)例中在軌保持三維軌道示意圖。

圖5本發(fā)明實(shí)例中在軌保持軌道x-y平面投影圖。

圖6本發(fā)明實(shí)例中在軌保持軌道x-z平面投影圖。

圖7本發(fā)明實(shí)例中在軌保持軌道y-z平面投影圖。

圖8實(shí)例中先技術(shù)在軌保持三維軌道示意圖。

具體實(shí)施方式

為了更好地說(shuō)明本發(fā)明的目的和優(yōu)點(diǎn)，下面通過(guò)對(duì)一個(gè)探測(cè)器在Halo軌道的在軌保持進(jìn)行實(shí)例分析，對(duì)本發(fā)明做出詳細(xì)解釋。

實(shí)施例1：

本發(fā)明公開(kāi)的考慮振幅約束的一種Halo軌道在軌保持方法，這里選擇由地球-月球-探測(cè)器構(gòu)成的限制性三體系統(tǒng)為例，平衡點(diǎn)選擇L2點(diǎn)，方案流程示意圖如圖1所示，Halo軌道的在軌保持設(shè)計(jì)方法包括如下步驟：

步驟一：在地球-月球-探測(cè)器構(gòu)成的限制性三體模型下建立動(dòng)力學(xué)方程，確定地球-月球-探測(cè)器構(gòu)成的三體系統(tǒng)平衡點(diǎn)位置。

選擇地球和月球分別作為主天體S₁和S₂，在質(zhì)心旋轉(zhuǎn)坐標(biāo)系下建立動(dòng)力學(xué)方程。該坐標(biāo)系選擇地月系統(tǒng)的質(zhì)心為原點(diǎn)，x軸方向由原點(diǎn)指向月球，z軸為月球公轉(zhuǎn)方向，y軸與x、z軸構(gòu)成右手坐標(biāo)系，坐標(biāo)系示意圖如圖2所示。則探測(cè)器的運(yùn)動(dòng)可以描述為式(1)：

其中μ＝m₂/(m₁+m₂)表示系統(tǒng)的質(zhì)量系數(shù)，m₁為地球質(zhì)量，m₂為月球質(zhì)量，分別為運(yùn)動(dòng)探測(cè)器到地球和月球的距離。

令式(1)中速度和加速度等于0，經(jīng)一系列推導(dǎo)和求解，可得五個(gè)平衡點(diǎn)(拉格朗日點(diǎn))，這5個(gè)平衡點(diǎn)均在x-y平面上。這里選擇L2平衡點(diǎn)作為Halo軌道部署位置，L2平衡點(diǎn)在x-y平面上位置坐標(biāo)為：

平衡點(diǎn)的位置分別示意圖如圖3所示。

步驟二：確定大主天體、小主天體和探測(cè)器構(gòu)成的三體系統(tǒng)下平衡點(diǎn)附近的Halo軌道。

為獲得更簡(jiǎn)潔的表達(dá)式，引入變量(ξ,η,ζ)，根據(jù)步驟一所得的平衡點(diǎn)的位置對(duì)旋轉(zhuǎn)坐標(biāo)系坐標(biāo)進(jìn)行替換，變量定義如下：

ξ＝x-x_Li；η＝y(tǒng)-y_Li；ζ＝z

平衡點(diǎn)附近的線性化運(yùn)動(dòng)方程可描述為式(2)：

式(2)中，ρ²＝x²+y²+z²；c₂(μ)、c_n(μ)為僅與質(zhì)量有關(guān)的常數(shù)，可表示為式(3)：

式(3)中，γ為平衡點(diǎn)與主天體S₂的距離，p_n為n階Legendre多項(xiàng)式。對(duì)方程(2)進(jìn)行分析，平衡點(diǎn)附近Halo軌道線性項(xiàng)可表示為式(4)：

式(4)中，ω₀分別為周期軌道運(yùn)動(dòng)的頻率，κ為常數(shù)，φ為Halo軌道相位；α、β分別為軌道平面和垂直振幅；這里選擇Halo軌道的垂直振幅為12000km，但為了滿足Halo軌道的周期性，要求平衡點(diǎn)附近Halo軌道的非線性項(xiàng)可表示為式(5)：

式(5)中，θ＝ω₀t+φ，i+j＝N稱為解的階數(shù)。利用式(4)和(5)作為平衡點(diǎn)附近Halo軌道的初值，通過(guò)多重打靶方法可以得到Halo軌道的精確數(shù)值解，即三體系統(tǒng)下平衡點(diǎn)附近的Halo軌道。

步驟三：根據(jù)擾動(dòng)變量設(shè)計(jì)Halo軌道保持的微分修正算法；根據(jù)微分修正算法得到Halo軌道精確數(shù)值解。

引入擾動(dòng)變量，相對(duì)于參考軌道的變分為(δx,δy,δz)，則六維狀態(tài)矢量為：

則變分方程的狀態(tài)空間形式表示為方程(6)：

與時(shí)間有關(guān)的矩陣A(t)是由4個(gè)3×3的矩陣構(gòu)成，即式(7)：

式(7)中B(t)是一個(gè)時(shí)變函數(shù)，因此A(t)也是一個(gè)時(shí)變函數(shù)，I₃是3×3的單位矩陣，C為常值矩陣，滿足如下表達(dá)式：

方程(6)的解的形式為式(8)：

這里Φ(t,t₀)是狀態(tài)轉(zhuǎn)移矩陣。狀態(tài)轉(zhuǎn)移矩陣是從初始狀態(tài)到t時(shí)刻狀態(tài)的線性映射，通過(guò)狀態(tài)轉(zhuǎn)移矩陣可估算出初始狀態(tài)變分對(duì)軌道遞推的影響。狀態(tài)轉(zhuǎn)移矩陣必須滿足矩陣微分方程(9)：

方程(9)的初始條件為Φ(t₀,t₀)＝I₆，這里I₆為6×6的單位陣。在t時(shí)刻的單位狀態(tài)轉(zhuǎn)移矩陣，通過(guò)初始條件的數(shù)值積分得到。因?yàn)闋顟B(tài)轉(zhuǎn)移矩陣是6×6，所以方程(9)的遞推可以通過(guò)36個(gè)一階微分方程的積分得到。B(t)的元素取決于參考軌道，因此求解A(t)，方程(9)需要同時(shí)積分非線性方程，從而得到狀態(tài)轉(zhuǎn)移矩陣Φ(t,t₀)。

根據(jù)微分修正算法求解Halo軌道精確數(shù)值解一般需要通過(guò)多次迭代過(guò)程來(lái)完成，歸結(jié)如下：

根據(jù)當(dāng)前末端狀態(tài)與理想狀態(tài)的偏差，通過(guò)狀態(tài)轉(zhuǎn)移矩陣對(duì)初始狀態(tài)進(jìn)行修正，使得最終的末端狀態(tài)滿足要求的約束條件。選取六維狀態(tài)矢量尋找初始狀態(tài)使周期軌道在t_f時(shí)刻滿足約束條件末端狀態(tài)偏差與初始狀態(tài)偏差的關(guān)系為式(10)：

矩陣的偏導(dǎo)數(shù)等于在t_f時(shí)刻的狀態(tài)轉(zhuǎn)移矩陣，那么方程(8)可以簡(jiǎn)化為方程(11)：

末端狀態(tài)的偏差量為方程(12)：

為目標(biāo)終端狀態(tài)，為實(shí)際終端狀態(tài)，將方程(12)代入方程(11)，可以解出一個(gè)初始狀態(tài)修正量的估計(jì)值從而得到三維周期Halo軌道的精確數(shù)值解。

步驟四：根據(jù)步驟三中的微分修正算法設(shè)計(jì)Halo軌道的在軌保持策略。

由于Halo軌道關(guān)于x-z平面對(duì)稱，周期軌道必定與x-z平面垂直，因此在交叉處有滿足式(13)：

利用垂直平面相交的特點(diǎn)進(jìn)一步對(duì)問(wèn)題進(jìn)行簡(jiǎn)化，為了滿足Halo軌道在半個(gè)周期后滿足垂直交叉的條件則需選擇y_f＝0作為積分終止的條件，在利用方程(11)迭代過(guò)程中需要調(diào)整初始狀態(tài)使得末端的狀態(tài)和接近于0，

由步驟三可知理想Halo軌道保持需要滿足垂直交叉條件，即滿足但在真實(shí)星歷環(huán)境下，嚴(yán)格滿足約束的Halo軌道是不存在的，只需保證Halo軌道的振幅尺寸滿足規(guī)定的范圍即可。因此對(duì)于Halo軌道的在軌保持修正，可以不嚴(yán)格滿足約束條件針對(duì)修正約束條件的嚴(yán)格性提出兩種不同的修正策略：寬松修正方法和嚴(yán)格修正方法。

寬松修正方法是指：軌道積分穿過(guò)x-z平面時(shí)x方向的速度為零，即嚴(yán)格修正方法是指：軌道積分穿過(guò)x-z平面時(shí)x方向和z方向的速度均為零，也即

當(dāng)軌道穿過(guò)x-z平面時(shí)z方向的振幅超過(guò)任務(wù)約束的任務(wù)上下邊界時(shí)執(zhí)行一次嚴(yán)格修正方法，否則執(zhí)行寬松修正方法。同時(shí)在每?jī)蓚€(gè)軌道周期內(nèi)執(zhí)行的4次修正中至少執(zhí)行1次嚴(yán)格修正策略。

步驟五：在真實(shí)星歷環(huán)境下，考慮測(cè)量誤差和執(zhí)行誤差，采用步驟四中的在軌保持策略進(jìn)行Halo軌道在軌保持。

軌道保持修正采用步驟三中的微分修正算法。在求解修正脈沖時(shí)，其積分初值為考慮測(cè)量誤差的實(shí)際狀態(tài)；而在軌道修正時(shí)，需要在實(shí)際狀態(tài)進(jìn)行脈沖修正時(shí)考慮修正的執(zhí)行誤差。這里星歷模型選擇DE405星歷，測(cè)量誤差位置精度1.6km(3σ)，速度精度1cm/s(3σ)，執(zhí)行誤差為推力方向誤差為1°(3σ)，推力大小誤差0.02m/s(3σ)。

在考慮測(cè)量誤差和執(zhí)行誤差的條件下，按照軌道保持策略采用微分修正算法得到每次軌道修正的速度增量，按照速度增量進(jìn)行軌道修正控制可以實(shí)現(xiàn)滿足振幅約束的Halo軌道在軌保持，同時(shí)盡可能降低軌道保持所需的燃料消耗。選擇在軌保持時(shí)間范圍為2018年6月1日～2021年6月1日。在軌保持3年的三維軌道示意圖如圖4所示，圖5～圖7分別為三維軌道示意圖在x-y，x-z和y-z平面的投影。

若采用先技術(shù)[2]中所述Halo軌道在軌保持控制方法，則在軌保持3年的三維軌道示意圖如圖8所示。本發(fā)明方法和先技術(shù)[2]中方法均以垂直振幅(z向振幅)12000km的Halo軌道為例，振幅上下邊界約束范圍為11500～12500km，分別采用相同在軌時(shí)間范圍和測(cè)量執(zhí)行誤差，打靶100次得到在軌保持3年的結(jié)果如表1所示。對(duì)比圖4和圖8和表1中數(shù)據(jù)可以看出，本發(fā)明方法相比先技術(shù)[2]中方法所需速度增量略多，但可以有效控制Halo軌道振幅范圍基本滿足約束，即長(zhǎng)期維持Halo軌道振幅不發(fā)散偏移。

表1本發(fā)明方法和先技術(shù)[2]方法結(jié)果對(duì)比

以上所述的具體描述，對(duì)發(fā)明的目的、技術(shù)方案和有益效果進(jìn)行了進(jìn)一步詳細(xì)說(shuō)明，所應(yīng)理解的是，以上所述僅為本發(fā)明的具體實(shí)施例，用于解釋本發(fā)明，并不用于限定本發(fā)明的保護(hù)范圍，凡在本發(fā)明的精神和原則之內(nèi)，所做的任何修改、等同替換、改進(jìn)等，均應(yīng)包含在本發(fā)明的保護(hù)范圍之內(nèi)。