本發明涉及一種超聲輔助加工聲學系統定振幅輸出的超聲電源功率調整模型的建模方法。

背景技術：

蜂窩復合材料具有的高比強度和高比剛度，以及耐高溫、絕緣性和不易燃燒等眾多優點，在航空航天、汽車、艦船和建筑等領域廣泛應用。但由于其結構的正交各向異性，使得蜂窩復合材料的高效高質加工成為推廣它更廣泛應用的瓶頸。超聲輔助加工技術引入蜂窩復合材料加工領域，能夠有效地解決傳統銑削加工中存在的粉塵污染嚴重、加工效率低下、被加工零件表面質量低等問題。根據蜂窩復合材料斷裂特性，對不同力學性能的蜂窩復合材料，理想的聲學系統輸出振幅各不相同。在超聲加工時，要求刀具的輸出振幅恒定在理想值附近，以使加工效率及加工質量最佳。考慮加工件幾何形狀、加工工藝和刀具的耐磨性，加工同一種蜂窩復合材料時可能選用不同材質、不同幾何形狀的刀具。根據聲學理論，刀具作為聲學系統的靜態負載、加工過程中切削力作為聲學系統的動態負載，都會影響刀具作為輸出端的振幅。但查閱眾多國內外文獻，目前少有學者就超聲輔助加工聲學系統的定振幅輸出技術進行相關研究，缺乏切實可行的為獲取超聲輔助加工聲學系統定振幅輸出，調整超聲電源功率的指導模型。

技術實現要素：

本發明提供了一種為了在采用不同刀具和加工工藝時，都能保證超聲加工特定蜂窩復合材料的定振幅輸出的超聲輔助加工聲學系統的超聲電源功率調整模型的建模方法。

本發明采用的技術方案是：

一種超聲輔助加工聲學系統的超聲電源功率調整模型的建模方法，其具體步驟如下：

步驟一，基于振幅參數關系式及ABAQUS有限元仿真諧響應分析，理論分析與超聲聲學系統振幅相關的參數與振幅的理論關系，其中振幅參數關系式為：

式中A₁、A₂、A₃、A₄為常數參數，Z_F為負載，I為電流，f為諧振頻率，A為振幅；

步驟二，以理論分析為基礎設計并搭建超聲輔助加工振幅測試實驗平臺，采用控制變量法分析各個參數對振幅的單因素影響及綜合影響并獲取樣本數據；

步驟三，借助MATLAB運用多元線性回歸分析法對樣本數據進行回歸分析并優化后建立以振幅為因變量的指導模型，以振幅為因變量的指導模型為：

A＝46.21+1.44P-2.18M+0.83L (2)

式中A為振幅，P為超聲電源功率，M為尖形刀質量，L為尖形刀長度；

步驟四，基于以振幅為因變量的指導模型為基礎進行反推得出超聲輔助加工聲學系統定振幅輸出的超聲電源功率調整模型，定振幅輸出的超聲電源功率調整模型為：

P＝0.69A+1.51M-0.58L-32.09 (3)

式中P為超聲電源功率，A為振幅，M為尖形刀質量，L為尖形刀長度；

步驟五，任選一把尖形刀對超聲電源功率調整模型進行實驗驗證。

進一步，步驟三中的以振幅為因變量的指導模型是通過多元線性回歸分析并利用殘差分析法進行優化后建立的。

本發明的構思是通過實驗研究參數對振幅的影響，然后借助MATLAB運用多元線性回歸分析法對實驗數據進行回歸分析建立以振幅為因變量的指導模型；進而反推得出超聲輔助加工聲學系統定振幅輸出的超聲電源功率調整模型；為實際加工的振幅調節提供理論指導。

本發明的有益效果：通過超聲電源功率調整模型對超聲電源的調整來保證在采用不同刀具和加工工藝時超聲加工特定蜂窩復合材料可以定振幅輸出。

附圖說明

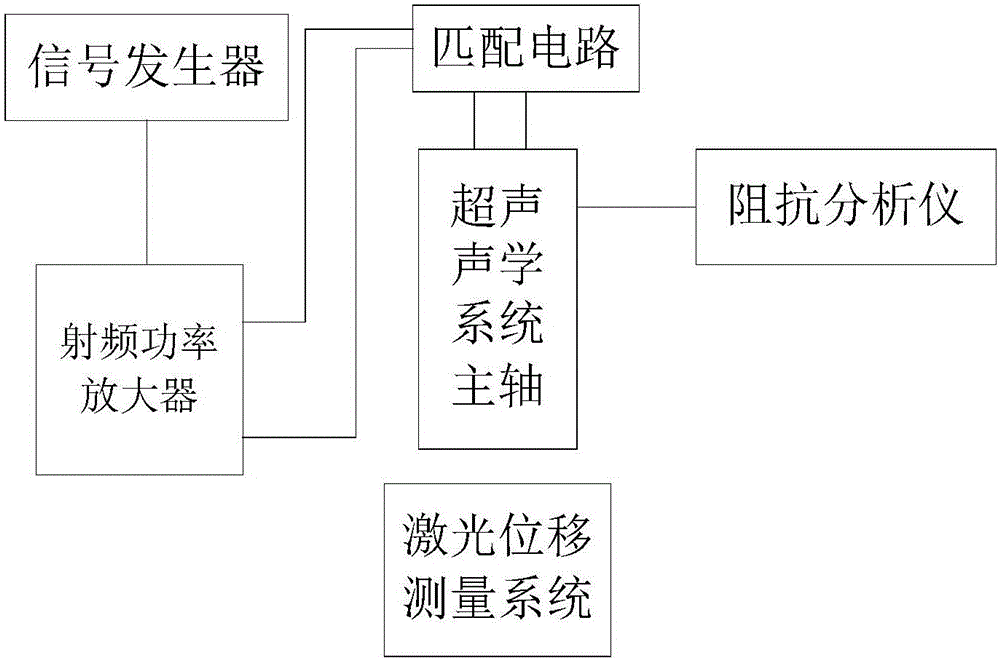
圖1是本發明的實驗原理圖。

圖2是本發明的建模方法實現流程圖。

具體實施方式

下面結合具體實施例來對本發明進行進一步說明，但并不將本發明局限于這些具體實施方式。本領域技術人員應該認識到，本發明涵蓋了權利要求書范圍內所可能包括的所有備選方案、改進方案和等效方案。

參見圖1-2，本發明超聲輔助加工聲學系統的超聲電源功率調整模型的建模方法，其具體步驟如下：

步驟一，振幅參數關系式為：

式中A₁、A₂、A₃、A₄為常數參數，Z_F為負載，I為電流，f為諧振頻率，A為振幅。通過公式(1)理論分析發現聲學系統的負載及電流對振幅有影響。其中，聲學系統的負載對振幅有反向作用，聲學系統的負載包括靜態負載和動態負載，刀具質量是超聲聲學系統的靜態負載。而電流對振幅起著促進作用，但聲學系統的電流值難以測得，且電源輸出電壓一定，因此電流可以等效成聲學系統電源功率對振幅的影響。另外，利用ABAQUS諧響應分析發現尖形刀長度對振幅有著促進作用。因此可以發現在靜態情況下，超聲輔助加工聲學系統的振幅受超聲功率、尖形刀質量及長度三個因素的影響。

步驟二，基于理論分析設計實驗，并根據實驗原理圖(如圖1所示)搭建實驗平臺。該實驗平臺包括超聲聲學系統主軸和激光位移測量系統，該超聲聲學系統主軸上連接有射頻功率放大器、阻抗分析儀、匹配電路，射頻功率放大器上連接有信號發生器并且與匹配電路連接。為便于研究單參數對振幅的影響，對尖形刀刀座部分進行鉆孔處理，使得長度同為38mm的尖形刀質量不同以及長度分別為38mm和48mm的尖形刀質量相同。通過振幅實驗研究超聲電源功率、尖形刀質量及長度對振幅的單參數影響及綜合影響，記錄各組實驗數據如表1、表2、表3所示。

從質量不同長度同為38mm的刀具振幅實驗數據表(如表1)可以看出質量越大的尖形刀，振幅越小；從質量相同長度不同的刀具振幅實驗數據表(如表2)可以看出刀具長度越長，振幅則會越大；另外，從長度質量均不同的刀具振幅實驗數據表(如表3)可以看出，從綜合影響上看，尖形刀長度變長時其質量的變化較小，因此對于未經預處理的尖形刀來說，其整體長度越長，振幅也越大。將三組實驗數據表可以發現，超聲電源功率越大，振幅越大且兩者數據之間基本呈線性關系。

表1質量不同長度同為38mm的刀具振幅實驗數據表

表2質量相同長度不同的刀具振幅實驗數據表

表3長度質量均不同的刀具振幅實驗數據表

步驟三，借助MATLAB運用多元回歸分析法對所做實驗數據進行回歸分析。首先利用MATLAB函數corrcoef對樣本數據進行相關性分析得到相關系數矩陣R及線性相關性檢驗矩陣P：

若是矩陣P中的值p_ij＜0.05時，則說明自變量之間具有明顯的相關性。可以發現尖形刀質量M與尖形刀長度L具有顯著的線性相關性。借助MATLAB中的函數LinearModel.fit進行回歸分析得到以振幅為因變量的指導模型：

A＝46.58+1.44P-2.20M+0.83L (6)

式中A為振幅，P為超聲電源功率，M為尖形刀質量，L為尖形刀長度。

為避免自變量之間的線性相關性而引起多重共線性，進而導致建模參數無效。本發明利用MATLAB自帶的基于方差膨脹因子的診斷方法對其進行共線診斷，發現不存在共線性。

對所完成的回歸分析式(6)進行殘差分析，完成異常值的查找并剔除。進而優化回歸方程得到以振幅為因變量的指導模型為：

A＝46.21+1.44P-2.18M+0.83L (2)

式中A為振幅，P為超聲電源功率，M為尖形刀質量，L為尖形刀長度。

步驟四，基于以振幅為因變量的指導模型反推得到超聲輔助加工聲學系統定振幅輸出的超聲電源功率調整模型：

P＝0.69A+1.51M-0.58L-32.09 (3)

式中P為超聲電源功率，A為振幅，M為尖形刀質量，L為尖形刀長度。

步驟五，由于實驗所用的超聲電源為E&I公司型號為1140LA的射頻功率放大器，其顯示功率的精度無法達到功率調整模型驗證實驗的精度要求。因此，本發明通過任意選取一把尖形刀對指導模型式(2)進行實驗驗證進而驗證超聲電源功率調整模型(3)。實驗數據如表4所示，結果顯示實際振幅與理論振幅的最大相對誤差僅為7.16％，表明了超聲輔助加工聲學系統定振幅輸出的超聲電源功率調整模型的有效性。

表4驗證實驗數據表

本發明的構思是通過實驗研究參數對振幅的影響，然后借助MATLAB運用多元線性回歸分析法對實驗數據進行回歸分析建立以振幅為因變量的指導模型；進而反推得出超聲輔助加工聲學系統定振幅輸出的超聲電源功率調整模型；為實際加工的振幅調節提供理論指導，通過超聲電源功率調整模型對超聲電源的調整來保證在采用不同刀具和加工工藝時超聲加工特定蜂窩復合材料可以定振幅輸出。