一種將馬爾可夫網絡等價轉換為因子圖的方法及系統與流程
本發明屬于概率圖模型技術領域,涉及概率圖模型之間的轉換技術,尤其是一種將馬爾可夫網絡等價轉換為因子圖的方法及系統。
背景技術:
概率(probability)在機器學習、模式識別、數據挖掘、大數據分析等智能分析推理技術領域起著核心作用。傳統的概率論(probability theory)可以用和規則(the sum rule)、積規則(the product rule)方程式來表示,所有概率推理和學習的代數操作(algebraic manipulations)都等同于反復應用這兩個簡單方程式。然而,借助概率圖模型(probabilistic graphical model),可將概率模型的底層代數表示(algebraic representations)等價變換成為直觀的圖形表示(graphical representations),這樣,概率推理和學習的復雜代數操作就可借助更為直觀、方便的圖操縱(graphical manipulations)來實現。
關于概率圖模型技術,可參閱全球最權威的學術專著:Daphne Koller and Nir Friedman.Probabilistic Graphical Models:Principles and Techniques.The MIT Press,2009.ISBN 978-0-262-01319-2(下文簡稱為《Probabilistic Graphical Models:Principles and Techniques》),該專著的中譯版為:作者:[美]Daphne Koller,[以色列]Nir Friedman;譯者:王飛躍,韓素青.概率圖模型:原理與技術.清華大學出版社,2015.ISBN:978-7-302-37134-2(下文簡稱為《概率圖模型:原理與技術》)。
概率圖模型是概率論(probability theory)與圖論(graph theory)相結合的產物,通過圖模型來表示概率分布(probability distributions),尤其是表示隨機變量之間的條件依賴(conditional dependence)關系與結構。一個概率圖模型通過連接線(links)——也稱邊(edges)或弧(arcs),來連接一對節點(nodes)——也稱頂點(vertices);每個節點表示一個隨機變量(random variables)(或隨機變量組),通過連接線來表示隨機變量之間的概率關系。于是,概率圖模型表示了代數上的一種因子分解(factorization)關系,即:定義在一個隨機變量集上的聯合分布可被分解成各自僅依賴于一個變量子集的函數(即因子)的乘積。
常用的概率圖模型包括有向圖模型(directed graphical models)和無向圖模型(undirected graphical models)。
有向圖模型常稱為貝葉斯網絡(Bayesian network)(參見:《Probabilistic Graphical Models:Principles and Techniques》,Section 3.2 Bayesian Networks,pages 51–68中的Definition 3.5,page 62;或者:《概率圖模型:原理與技術》,3.2貝葉斯網,pages 51–68,定義3.5,page 61),適用于表示隨機變量之間的因果關系(causal relationships)。
無向圖模型常稱為馬爾可夫隨機場(Markov random field,MRF)或馬爾可夫網絡(Markov network)(參見:《Probabilistic Graphical Models:Principles and Techniques》,Section 4.2.2Gibbs Distributions and Markov Networks,pages 108–110中的Definition 4.3,page 108和Definition 4.4,page 109;或者:《概率圖模型:原理與技術》,4.2.2吉布斯分布與馬爾可夫網,pages 107–109中的定義4.3,page 107和定義4.4,page 108),適用于表示隨機變量之間的軟約束(soft constraints)。馬爾可夫網絡是一個無向圖,其中,每個節點表示一個隨機變量,每條無向邊連接一對隨機變量節點,圖中表示了若干個稱為最大團(maximal clique)的最大完全子圖(maximal complete subgraph),所謂最大完全子圖就是該子圖中的所有節點對均通過一條無向邊進行連接,且該子圖中再增加圖中任何節點將不具有這種性質,在每個最大團中所有節點所對應的若干個隨機變量上定義了一個稱為最大團勢(maximal clique potential)的函數,且這些最大團勢函數均是非負函數,于是,馬爾可夫網絡在代數上表示了這樣一種因子分解(factorization)關系:定義在所有隨機變量上的聯合分布可表示為所有最大團勢函數(即因子)的乘積再乘以一個歸一化因子(normalization factor),該歸一化因子是一個歸一化系數(normalization coefficient),可看成是一個定義在隨機變量空集上的常值函數(constant function),它是稱為配分函數(partition function)的歸一化常數(normalization constant)的倒數。
因子圖(factor graph)是一種新穎的無向圖模型(參見:《Probabilistic Graphical Models:Principles and Techniques》,Section 4.4.1.1 Factor Graphs,pages 123–124,Definition 4.13,page 123;或者:《概率圖模型:原理與技術》,4.4.1.1因子圖,pages 121–122,定義4.13,page122)。因子圖是由變量節點與因子(factor)節點所構成的一個二分圖(bipartite graph),因子或因子節點也稱為局部函數(local function),在因子圖中,每個變量節點表示變量集中的一個變量,每個因子節點表示定義在變量子集上的一個局部函數,當且僅當某個變量是一個局部函數的自變量(argument)時,該變量節點與該因子節點之間有一條無向邊,于是,定義在變量集上的一個全局函數(global function)可表示為所有定義在變量子集上的局部函數(即因子)的乘積;當全局函數用于表示一組隨機變量的聯合分布時,因子圖成為一種新穎的概率圖模型。因子圖模型的突出優勢在于概率推理的代數操作可借助因子圖上的高效率的推理算法來實現。
概率圖模型之間的相互轉換技術有利于復用已有的概率模型,簡化概率建模過程,從而促進概率圖模型在機器學習、模式識別、數據挖掘、大數據分析等智能分析推理技術領域中的應用。貝葉斯網絡、馬爾可夫網絡等傳統概率圖模型之間的相互轉換已存在相應的方法,例如,從貝葉斯網絡到馬爾可夫網絡的轉換方法(參見:《Probabilistic Graphical Models:Principles and Techniques》,Section 4.5.1 From Bayesian Networks to Markov Networks,pages 134–137;或者:《概率圖模型:原理與技術》,4.5.1從貝葉斯網到馬爾可夫網,pages 132–136),從馬爾可夫網絡到貝葉斯網絡的轉換方法(參見:《Probabilistic Graphical Models:Principles and Techniques》,Section 4.5.2 From Markov Networks to Bayesian Networks,pages 137–139;或者:《概率圖模型:原理與技術》,4.5.2從馬爾可夫網到貝葉斯網,pages 136–138)。然而,傳統概率圖模型向因子圖這樣的新穎概率圖模型的等價轉換,目前尚缺乏相應的方法,也缺乏完整、可實施的技術方案。本發明的目的就是提供一種將馬爾可夫網絡等價轉換為因子圖的方法及系統。所謂“等價轉換”就是,雖然轉換前后的兩種概率圖模型在圖形表示上完全不同,但它們在代數上所表示的聯合分布的因子分解關系是完全等價的。
技術實現要素:
本發明所要解決的技術問題是提供一種將馬爾可夫網絡等價轉換為因子圖的方法及系統,從而克服目前缺乏馬爾可夫網絡向因子圖等價轉換的完整、可實施技術方案的缺陷。
為解決上述技術問題,本發明是通過以下技術方案實現的:
根據本發明的一個方面,提供了一種將馬爾可夫網絡等價轉換為因子圖的方法,包括下列步驟:
S1:輸入待轉換為因子圖的馬爾可夫網絡;
S2:依次按轉換規則1、2和3將馬爾可夫網絡等價轉換為因子圖:
轉換規則1:創建因子圖的所有變量節點,它們分別對應于馬爾可夫網絡的所有隨機變量節點;
轉換規則2:創建因子圖的所有因子節點即局部函數,它們分別對應于馬爾可夫網絡中表示的所有最大團勢函數;
轉換規則3:當且僅當因子圖中某個變量是一個局部函數的自變量時,添加連接該變量節點與該局部函數即因子節點的無向邊;
S3:輸出轉換成的因子圖。
在該方法中,所述步驟S1中的馬爾可夫網絡進一步包括:
馬爾可夫網絡的圖形表示如下:作為一種概率圖模型,馬爾可夫網絡是一個無向圖,其中,每個節點對應一個隨機變量,每條無向邊連接一對隨機變量節點,圖中表示了若干個稱為最大團的最大完全子圖,在每個最大團中所有節點所對應的若干個隨機變量上定義了一個稱為最大團勢的函數,且這些最大團勢函數均是非負函數,于是,馬爾可夫網絡在代數上表示了這樣一種因子分解關系:定義在所有隨機變量上的聯合分布可表示為所有最大團勢函數的乘積再乘以一個歸一化因子,該歸一化因子是一個歸一化系數,可看成是一個定義在隨機變量空集上的常值函數,它是稱為配分函數的歸一化常數的倒數;
馬爾可夫網絡的代數表示如下:馬爾可夫網絡MN(X,L)表示為一個聯合分布的因子分解關系其中,p(X)是定義在隨機變量集X={x1,...,xK}上的聯合分布,Z-1是該因子分解中的歸一化因子,配分函數是一個歸一化常數,每個因子是定義在最大團Cn中所有節點所對應的隨機變量子集上的一個最大團勢函數,每個最大團是一個最大完全子圖,其中所有節點對均通過一條無向邊進行連接,所有這樣的無向邊構成馬爾可夫網絡MN(X,L)的無向邊集L。
在該方法中,所述步驟S1中的因子圖進一步包括:
因子圖的圖形表示如下:因子圖是由變量節點與因子節點所構成的一個二分圖,其中,每個變量節點表示變量集中的一個變量,每個因子節點表示定義在變量子集上的一個局部函數,當且僅當某個變量是一個局部函數的自變量時,該變量節點與該因子節點之間有一條無向邊,于是,定義在變量集上的一個全局函數可表示為所有定義在變量子集上的局部函數的乘積;當全局函數用于表示一組隨機變量的聯合分布時,因子圖成為一種新穎的概率圖模型;
因子圖的代數表示如下:因子圖FG(X,F,E)表示為一個全局函數的因子分解關系其中,h(X)是定義在變量集X={x1,...,xK}上的全局函數,每個局部函數fj(Xj),j∈{1,...,J}稱為定義在變量子集上的一個因子,所有這樣的局部函數構成因子圖FG(X,F,E)的局部函數集F={f1,...,fJ},同時,因子圖FG(X,F,E)的無向邊集E={(xj,fj)|iif xj∈Xj};當全局函數h(X)用于表示定義在隨機變量集X上的聯合分布時,因子圖FG(X,F,E)成為一個概率圖模型。
在該方法中,所述步驟S2中的轉換規則1、2和3進一步包括:
轉換規則1的代數表示如下:將馬爾可夫網絡MN(X,L)中全部K個隨機變量xk∈X,k∈{1,...,K}對應地轉換為因子圖FG(X,F,E)中的K個變量
轉換規則2的代數表示如下:將馬爾可夫網絡MN(X,L)中全部N個最大團勢函數對應地轉換為因子圖FG(X,F,E)中J=N個局部函數fj∈F,j∈{1,...,J};
轉換規則3的代數表示如下:令因子圖FG(X,F,E)中全部J=N個局部函數fj∈F,j∈{1,...,J}分別表示馬爾可夫網絡MN(X,L)中N個最大團勢函數,即這些因子圖局部函數它們表示了因子圖的無向邊集E={(xj,fj)|iif xj∈Xj};令該因子圖的全局函數h(X)表示定義在隨機變量集X上的聯合分布再乘以該馬爾可夫網絡中的歸一化常數Z,即:h(X)=p(X)×Z;于是,該因子圖所表示的因子分解關系即為它等價于J=N,該因子分解關系與馬爾可夫網絡MN(X,L)所表示的因子分解關系完全等價。
根據本發明的另一個方面,還提供了一種將馬爾可夫網絡等價轉換為因子圖的系統,包括:馬爾可夫網絡輸入模塊、馬爾可夫網絡向因子圖等價轉換模塊、因子圖輸出模塊、人機交互界面,其中:
所述馬爾可夫網絡輸入模塊用于實現輸入待轉換為因子圖的馬爾可夫網絡;
所述馬爾可夫網絡向因子圖等價轉換模塊進一步包括三個子模塊:因子圖的變量節點創建子模塊、因子圖的因子節點創建子模塊和因子圖的無向邊添加子模塊,它們依次分別按轉換規則1、2和3實現將馬爾可夫網絡等價轉換為因子圖;
上述轉換規則1、2和3具體為:
轉換規則1:創建因子圖的所有變量節點,它們分別對應于馬爾可夫網絡的所有隨機變量節點;
轉換規則2:創建因子圖的所有因子節點即局部函數,它們分別對應于馬爾可夫網絡中表示的所有最大團勢函數;
轉換規則3:當且僅當因子圖中某個變量是一個局部函數的自變量時,添加連接該變量節點與該局部函數即因子節點的無向邊;
所述因子圖輸出模塊用于實現輸出轉換成的因子圖;
所述人機交互界面用于實現用戶與該系統之間的人機交互,包括:用戶通過此界面輸入并圖示一個馬爾可夫網絡,用戶通過此界面提交馬爾可夫網絡向因子圖等價轉換的執行指令,用戶通過此界面輸出并圖示一個轉換成的因子圖。
本發明的有益技術效果主要包括三個方面:(1)克服了目前缺乏馬爾可夫網絡向因子圖等價轉換的完整、可實施技術方案的缺陷;(2)所提供的轉換方法簡單易行、轉換系統易于實現;(3)所提供的轉換方法及系統在概率建模與推理、機器學習、模式識別、數據挖掘、大數據分析等領域具有廣闊的應用前景。
下面結合附圖對本發明的具體實施方式作進一步的描述。本發明附加的方面和優點將在下面的描述中部分給出,這些將從下面的描述中變得明顯,或通過本發明的實踐了解到。
附圖說明
圖1是根據本發明技術方案的一種將馬爾可夫網絡等價轉換為因子圖的方法的步驟流程圖;
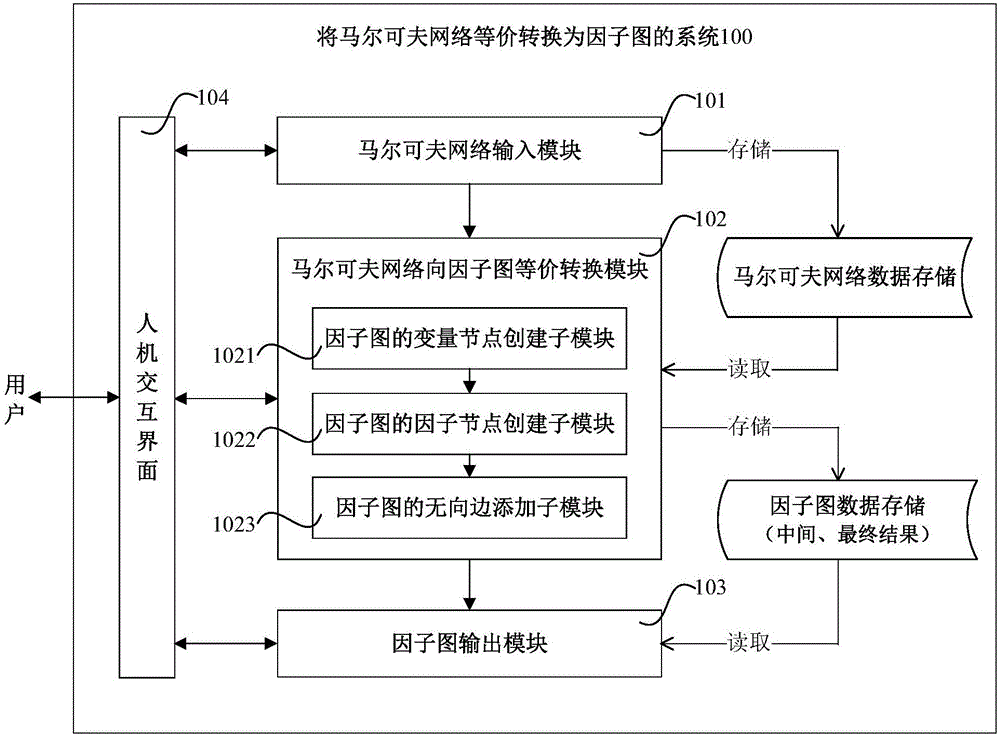
圖2是根據本發明技術方案的一種將馬爾可夫網絡等價轉換為因子圖的系統的模塊結構與處理流程圖,圖中符號遵循國家標準GB 1526-89(等同于國際標準ISO 5807-1985);
圖3是本發明的一個優選實施例中馬爾可夫網絡向因子圖等價轉換的過程與規則的示意。
具體實施方式
下面詳細描述本發明的實施方式,所述實施方式的示例在附圖中示出,其中自始至終相同或類似的標號表示相同或類似的概念、對象、要素等或具有相同或類似功能的概念、對象、要素等。下面通過參考附圖描述的實施方式是示例性的,僅用于解釋本發明,而不能解釋為對本發明的限制。
本技術領域技術人員可以理解,除非另外定義,這里使用的所有術語(包括技術術語和科學術語)具有與本發明所屬領域及相關領域中的普通技術人員的一般理解相同的意義。還應該理解的是,諸如通用字典中定義的那些術語應該被理解為具有與現有技術的上下文中的意義一致的意義,并且除非像這里一樣定義,不會用理想化或過于正式的含義來解釋。
為了解決上述技術問題,本發明是通過以下技術方案實現的:
根據本發明的一個方面,提供了一種將馬爾可夫網絡等價轉換為因子圖的方法,如圖1所示,包括下列步驟:
S1:輸入待轉換為因子圖的馬爾可夫網絡,所述馬爾可夫網絡進一步包括:
馬爾可夫網絡的圖形表示如下:作為一種概率圖模型,馬爾可夫網絡是一個無向圖,其中,每個節點對應一個隨機變量,每條無向邊連接一對隨機變量節點,圖中表示了若干個稱為最大團的最大完全子圖,在每個最大團中所有節點所對應的若干個隨機變量上定義了一個稱為最大團勢的函數,且這些最大團勢函數均是非負函數,于是,馬爾可夫網絡在代數上表示了這樣一種因子分解關系:定義在所有隨機變量上的聯合分布可表示為所有最大團勢函數的乘積再乘以一個歸一化因子,該歸一化因子是一個歸一化系數,可看成是一個定義在隨機變量空集上的常值函數,它是稱為配分函數的歸一化常數的倒數;
馬爾可夫網絡的代數表示如下:馬爾可夫網絡MN(X,L)表示為一個聯合分布的因子分解關系其中,p(X)是定義在隨機變量集X={x1,...,xK}上的聯合分布,Z-1是該因子分解中的歸一化因子,配分函數是一個歸一化常數,每個因子是定義在最大團Cn中所有節點所對應的隨機變量子集上的一個最大團勢函數,每個最大團是一個最大完全子圖,其中所有節點對均通過一條無向邊進行連接,所有這樣的無向邊構成馬爾可夫網絡MN(X,L)的無向邊集L。
上述因子圖進一步包括:
因子圖的圖形表示如下:因子圖是由變量節點與因子節點所構成的一個二分圖,其中,每個變量節點表示變量集中的一個變量,每個因子節點表示定義在變量子集上的一個局部函數,當且僅當某個變量是一個局部函數的自變量時,該變量節點與該因子節點之間有一條無向邊,于是,定義在變量集上的一個全局函數可表示為所有定義在變量子集上的局部函數的乘積;當全局函數用于表示一組隨機變量的聯合分布時,因子圖成為一種新穎的概率圖模型;
因子圖的代數表示如下:因子圖FG(X,F,E)表示為一個全局函數的因子分解關系其中,h(X)是定義在變量集X={x1,...,xK}上的全局函數,每個局部函數fj(Xj),j∈{1,...,J}稱為定義在變量子集上的一個因子,所有這樣的局部函數構成因子圖FG(X,F,E)的局部函數集F={f1,...,fJ},同時,因子圖FG(X,F,E)的無向邊集E={(xj,fj)|iif xj∈Xj};當全局函數h(X)用于表示定義在隨機變量集X上的聯合分布時,因子圖FG(X,F,E)成為一個概率圖模型。
S2:依次按轉換規則1、2和3將馬爾可夫網絡等價轉換為因子圖:
轉換規則1:創建因子圖的所有變量節點,它們分別對應于馬爾可夫網絡的所有隨機變量節點;
轉換規則1的代數表示如下:將馬爾可夫網絡MN(X,L)中全部K個隨機變量xk∈X,k∈{1,...,K}對應地轉換為因子圖FG(X,F,E)中的K個變量
轉換規則2:創建因子圖的所有因子節點即局部函數,它們分別對應于馬爾可夫網絡中表示的所有最大團勢函數;
轉換規則2的代數表示如下:將馬爾可夫網絡MN(X,L)中全部N個最大團勢函數對應地轉換為因子圖FG(X,F,E)中J=N個局部函數fj∈F,j∈{1,...,J};
轉換規則3:當且僅當因子圖中某個變量是一個局部函數的自變量時,添加連接該變量節點與該局部函數即因子節點的無向邊;
轉換規則3的代數表示如下:令因子圖FG(X,F,E)中全部J=N個局部函數fj∈F,j∈{1,...,J}分別表示馬爾可夫網絡MN(X,L)中N個最大團勢函數,即這些因子圖局部函數它們表示了因子圖的無向邊集E={(xj,fj)|iif xj∈Xj};令該因子圖的全局函數h(X)表示定義在隨機變量集X上的聯合分布再乘以該馬爾可夫網絡中的歸一化常數Z,即:h(X)=p(X)×Z;于是,該因子圖所表示的因子分解關系即為它等價于J=N,該因子分解關系與馬爾可夫網絡MN(X,L)所表示的因子分解關系完全等價。
S3:輸出轉換成的因子圖FG(X,F,E)。
以本發明的上述方法為基礎,可以進一步構建一種將馬爾可夫網絡等價轉換為因子圖的系統100,如圖2所示,包括:馬爾可夫網絡輸入模塊101、馬爾可夫網絡向因子圖等價轉換模塊102、因子圖輸出模塊103、人機交互界面104,其中:
所述馬爾可夫網絡輸入模塊101用于實現本發明方法中的步驟S1:輸入待轉換為因子圖的馬爾可夫網絡;
所述馬爾可夫網絡向因子圖等價轉換模塊102用于實現本發明方法中的步驟S2:依次按轉換規則1、2和3將馬爾可夫網絡等價轉換為因子圖;該模塊進一步包括三個子模塊:因子圖的變量節點創建子模塊1021、因子圖的因子節點創建子模塊1022和因子圖的無向邊添加子模塊1023,它們依次分別按轉換規則1、2和3實現將馬爾可夫網絡等價轉換為因子圖:
轉換規則1:創建因子圖的所有變量節點,它們分別對應于馬爾可夫網絡的所有隨機變量節點;
轉換規則2:創建因子圖的所有因子節點即局部函數,它們分別對應于馬爾可夫網絡中表示的所有最大團勢函數;
轉換規則3:當且僅當因子圖中某個變量是一個局部函數的自變量時,添加連接該變量節點與該局部函數即因子節點的無向邊;
所述因子圖輸出模塊103用于實現本發明方法中的步驟S3:輸出轉換成的因子圖;
所述人機交互界面104用于實現用戶與該系統之間的人機交互,包括:用戶通過此界面輸入并圖示一個馬爾可夫網絡,用戶通過此界面提交馬爾可夫網絡向因子圖等價轉換的執行指令,用戶通過此界面輸出并圖示一個轉換成的因子圖。
上述將馬爾可夫網絡等價轉換為因子圖的系統100可采用的實現技術包括:
馬爾可夫網絡輸入模塊101可采用常規的程序設計語言(如:C++、Java、Python、R等)通過編程及函數調用來實現,輸入的馬爾可夫網絡以數據文件的形式進行存儲,數據存儲格式可采用一般的無向圖(undirected graph,UG)的數據存儲格式(如:文本文件、CSV文件、XML文檔等);作為一個可選項,輸入的馬爾可夫網絡可進一步以無向圖(UG)的形式在人機交互界面104進行圖示。
馬爾可夫網絡向因子圖等價轉換模塊102可采用常規的程序設計語言(如:C++、Java、Python、R等)通過編程實現;轉換過程中,需讀取已存儲的馬爾可夫網絡數據文件,產生的因子圖中間結果和最終結果以數據文件的形式進行存儲,數據存儲格式可采用一般的二分圖(bipartite graph,BG)的數據存儲格式(如:文本文件、CSV文件、XML文檔等)。
因子圖輸出模塊103可采用常規的程序設計語言(如:C++、Java、Python、R等)通過編程及函數調用來實現,通過讀取已存儲的因子圖(最終結果)數據文件,以二分圖(BG)的形式在人機交互界面104進行圖示。
人機交互界面104可使用常規的人機交互界面實現技術,其中,基于已存儲的圖數據,輸入的馬爾可夫網絡可采用一般的無向圖(UG)可視化技術在界面上進行顯示,轉換所得的因子圖可采用一般的二分圖(BG)可視化技術在界面上進行圖示,兩者的圖示也可以通過調用開源的圖模型工具包中的有關函數來實現,如工具包GMTK—The Graphical Models Toolkit(http://melodi.ee.washington.edu/gmtk/)。
下面再通過一個優選實施例來進一步描述本發明技術方案的具體實施方式,并進一步具體表明本發明的前述有益技術效果。本優選實施例中馬爾可夫網絡向因子圖等價轉換的過程與規則如圖3所示。
本發明的一種將馬爾可夫網絡等價轉換為因子圖的方法,如圖3所示,包括下列步驟:
S1:輸入待轉換為因子圖的馬爾可夫網絡;不失一般性,設輸入的馬爾可夫網絡MN如圖3(A)所示,本實施例的具體情況如下:
馬爾可夫網絡MN的圖形表示如圖3(A)所示:該馬爾可夫網絡是一個含有7個隨機變量節點的無向圖,定義在所有隨機變量上的聯合分布可表示為所有最大團勢函數的乘積再乘以一個歸一化因子Z-1。
馬爾可夫網絡MN的代數表示如圖3(A)的右側所示:定義在隨機變量集X={x1,...,x7}上的聯合分布p(X)=p(x1,...,x7),定義在全部3個最大團C1,C2,C3所對應的隨機變量子集上的最大團勢函數分別是于是,該馬爾可夫網絡所表示的聯合分布的因子分解關系具體為:
S2:依次按轉換規則1、2和3將馬爾可夫網絡等價轉換為因子圖:
轉換規則1:創建因子圖的所有變量節點,它們分別對應于馬爾可夫網絡的所有隨機變量節點;
轉換規則1的代數表示如下:將馬爾可夫網絡MN(X,L)中全部K個隨機變量xk∈X,k∈{1,...,K}對應地轉換為因子圖FG(X,F,E)中的K個變量如圖3(A)到圖3(B-1)之間的“第一步轉換”所示,本實施例的具體情況如下:
創建的因子圖變量為:x1,...,x7分別對應于馬爾可夫網絡MN的隨機變量x1,...,x7。
轉換規則2:創建因子圖的所有因子節點即局部函數,它們分別對應于馬爾可夫網絡中表示的所有最大團勢函數;
轉換規則2的代數表示如下:將馬爾可夫網絡MN(X,L)中全部N個最大團勢函數對應地轉換為因子圖FG(X,F,E)中J=N個局部函數fj∈F,j∈{1,...,J};如圖3(B-1)到圖3(B-2)之間的“第二步轉換”所示,本實施例的具體情況如下:
創建的因子圖的所有因子節點即局部函數具體為:f1,f2,f3分別對應于馬爾可夫網絡MN所表示的上述最大團勢函數:
轉換規則3:當且僅當因子圖中某個變量是一個局部函數的自變量時,添加連接該變量節點與該局部函數即因子節點的無向邊;
轉換規則3的代數表示如下:令因子圖FG(X,F,E)中全部J=N個局部函數fj∈F,j∈{1,...,J}分別表示馬爾可夫網絡MN(X,L)中N個最大團勢函數,即這些因子圖局部函數它們表示了因子圖的無向邊集E={(xj,fj)|iif xj∈Xj};令該因子圖的全局函數h(X)表示定義在隨機變量集X上的聯合分布再乘以該馬爾可夫網絡中的歸一化常數Z,即:h(X)=p(X)×Z;于是,該因子圖所表示的因子分解關系即為它等價于J=N,該因子分解關系與馬爾可夫網絡MN(X,L)所表示的因子分解關系完全等價;如圖3(B-2)到圖3(B-3)之間的“第三步轉換”所示,本實施例的具體情況如下:
令因子圖FG中全部3個局部函數f1,f2,f3分別表示馬爾可夫網絡MN中最大團勢函數:
這些局部函數對應表示了因子圖FG的無向邊集:
E={(x1,f1),(x2,f1),(x2,f2),(x3,f2),(x4,f2),(x4,f3),(x5,f3),(x6,f3),(x7,f3)}。
令因子圖FG的全局函數h(X)表示定義在隨機變量集X={x1,...,x7}上的聯合分布再乘以馬爾可夫網絡MN中歸一化常數Z,即h(X)=p(X)×Z。于是,因子圖FG所表示的全局函數的因子分解關系具體為:
它等價于:
以上因子分解與馬爾可夫網絡BN所表示的聯合分布的因子分解關系完全等價,表明已將馬爾可夫網絡等價轉換為因子圖。
S3:輸出轉換成的因子圖,本實施例的具體情況如下:
輸出轉換成的因子圖FG,見圖3(B-3),該因子圖由馬爾可夫網絡BN等價轉換而得。
由本發明上述技術方案(包括方法及系統)及其具體實施方式(包括優選實施例)可理解出各處理步驟的技術效果和所解決的技術問題如下:
步驟S1所取得的技術效果是:輸入了待轉換為因子圖的馬爾可夫網絡,該馬爾可夫網絡的圖形表示及對應的代數表示可進行數據存儲;從而解決了技術問題:如何輸入待轉換為因子圖的馬爾可夫網絡。這樣,為本發明總體技術問題的解決創造了不可或缺的必要條件。
步驟S2所取得的技術效果是:基于馬爾可夫網絡數據存儲,將馬爾可夫網絡的圖形表示及對應的代數表示等價轉換為因子圖的圖形表示及對應的代數表示,并可進行數據存儲;從而解決了技術問題:如何將馬爾可夫網絡等價轉換為因子圖。這樣,為本發明總體技術問題的解決創造了不可或缺的必要條件。
步驟S3所取得的技術效果是:基于轉換所得的因子圖數據存儲,輸出等價轉換成的因子圖;從而解決了技術問題:如何輸出轉換成的因子圖。這樣,為本發明總體技術問題的解決創造了不可或缺的必要條件。
總體來說,由本發明上述技術方案及其具體實施方式可以理解的是,本發明的有益技術效果主要包括三個方面:(1)克服了目前缺乏馬爾可夫網絡向因子圖等價轉換的完整、可實施技術方案的缺陷;(2)所提供的轉換方法簡單易行、轉換系統易于實現;(3)所提供的轉換方法及系統在概率建模與推理、機器學習、模式識別、數據挖掘、大數據分析等領域具有廣闊的應用前景。
以上所述僅是本發明的部分實施方式,應當指出,對于本技術領域的普通技術人員來說,在不脫離本發明原理的前提下,還可以做出若干改進和潤飾,這些改進和潤飾也應視為本發明的保護范圍。
- 還沒有人留言評論。精彩留言會獲得點贊!