本發明涉及計算機視覺領域，尤其涉及一種基于二次曲線透視投影不變性的單相機位姿估計方法。

背景技術：

單相機位姿估計問題是計算機視覺、攝影測量學領域一個重要的研究問題。該問題的基本描述可以歸結為：已經圖像空間和物理空間的特征對應信息，求解兩個空間下定義的不同坐標系之間的位姿約束，即估計旋轉參數和平移參數。而單相機位姿估計方法的準確性直接影響到計算機視覺研究領域的視覺追蹤、攝影測量、相機標定等任務的完成質量。

由于在平面目標透視投影過程中，點、直線和二次曲線具有不變性，現有的單相機位姿估計方法所采用的特征對應信息主要有特征點對應性、特征直線對應性和特征二次曲線對應性三種。對于基于特征點對應性的估計方法，特征點對應信息的獲取容易收到圖像噪聲和像面坐標提取方法精度的影響，間接影響到了位姿估計的精度。文獻“Fast and Globally Convergent Pose Estimation from Video Images”(C.P.Lu,G.D.Hager,and E.Mjolsness.IEEE Transactions on Pattern Analysis&Machine Intelligence,vol.22,pp.610-622,2000.)提出一種利用旋轉矩陣正交參數化，建立合適的目標函數。該方法估計精度高，計算效率高，對初值的依賴程度小。但是旋轉矩陣正交參數化容易受到輸入數據的噪聲的影響，導致其迭代過程退化。文獻“EPnP:An Accurate O(n)Solution to the PnP Problem”(V.Lepetit,F.Moreno-Noguer,and P.Fua.International Journal of Computer Vision,vol.81,pp.155-166,2009.)，該方法將輸入的實際控制點由四個虛擬控制點等價轉換，進而將問題歸結于估計四個虛擬控制點在相機坐標系下的坐標，其能夠在線性算法時間復雜度O(n)中完成，但是由于數據噪聲的影響，常常會出現多解的結果。對于基于特征直線對應性的估計方法，直線長度的不確定性導致了圖像上成像線段特征具有不確定性，同時，直線特征較為簡單，很容易受到環境中噪聲紋理誤檢測的影響。而相比于直線具有更高階次的二次曲線，如橢圓，其紋理特征相比直線更容易從環境紋理中識別分離出來，同時在特征提取方面，具有更穩健的特性。

技術實現要素：

本發明的目的在于通過一種基于二次曲線透視投影不變性的單相機位姿估計方法，來解決以上背景技術部分提到的問題。

為達此目的，本發明采用以下技術方案：

一種基于二次曲線透視投影不變性的單相機位姿估計方法，該方法包括如下步驟：

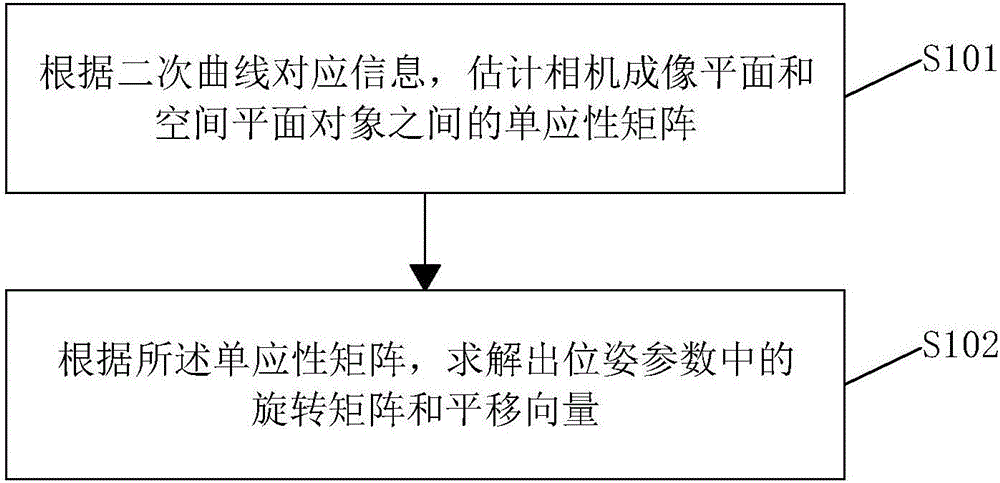
S101、根據二次曲線對應信息，估計相機成像平面和空間平面對象之間的單應性矩陣；

S102、根據所述單應性矩陣，求解出位姿參數中的旋轉矩陣和平移向量。

特別地，所述步驟S101包括：所述單應性矩陣指一個二維平面對象上的點與相機成像平面上的像點之間的映射關系；

相機的透視投影模型為：

其中，為相機坐標系下成像平面上點的齊次坐標，為世界坐標系下平面對象上點的齊次坐標；K是相機的內參數矩陣，其具體包括主點坐標、焦距參數，s為尺度因子；設[R t]為世界坐標系轉化到相機坐標系下的位姿參數；旋轉矩陣R可進行列向量的形式來表示，則：

[R t]＝[r₁ r₂ r₃ t] (2)

由于對象為平面物體，故則公式(1)表達為：

設H＝K[r₁r₂t]，公式(3)表達為

H即是世界坐標系平面與圖像平面的單應性映射；

平面內，二次曲線的代數方程可表示為：

Ax²+Bxy+Cy²+Dx+Ey+F＝0 (5)

使用矩陣的形式表達公式(5)，具體為：

根據公式(6)，平面對象上二次曲線上的點和二次曲線方程的關系表示為如下式：

根據二次曲線透視投影不變性，世界坐標系下二次曲線在成像平面上的透視投影成像也是二次曲線；同理，根據公式(7)，成像平面上二次曲線上的點和二次曲線方程的關系可以表示為如下式：

其中，C′表示成像平面二次曲線代數方程的矩陣參數；

將公式(4)帶入公式(8)，可得：

聯立公式(7)、(9)，得出世界坐標系內的二次曲線和成像平面內的二次曲線之間的關系，即：

C＝sH^TC'H (10)

不失一般性的，限定兩個矩陣行列式值得情況下，將(10)表達為：

C＝H^TC'H (11)

其中：det(H)＝1，det(C)＝1，det(C')＝1。

特別地，所述步驟S101還包括：聯立同一平面內兩組二次曲線對應性等式方程，將求解單應性矩陣方程由非線性方程轉化成線性方程求解，過程如下：

設空間有n個二次曲線C_i，i＝1,2,3....n，所有的空間二次曲線在一個平面上,其在成像平面上的對應的二次曲線為C_i'，i＝1,2,3....n，且空間的n個二次曲線在同一個世界坐標系下；對于兩組二次曲線對應信息，建立如下等式：

C_i^-1C_j＝H^-1C_i'^-1C_j'H (12)

由公式(12)可得，

C_i'^-1C_j'H-HC_i^-1C_j＝0 (13)

其可以轉化為線性方程：

M_ijh＝0 (14)

其中：h＝[H₁₁ H₂₁ H₃₁ H₁₂ H₂₂ H₃₂ H₁₃ H₂₃ H₃₃]^T，

設定

當二次曲線對應信息個數大于兩個時，公式(14)的求解應該歸結于超定線性方程組的求解；利用最小二乘方法得到單應性矩陣的最優解。

特別地，所述步驟S102包括：相機的內參數矩陣為K，單應性矩陣為H，則：

[r₁ r_2t]＝HK^-1 (15)

由于旋轉矩陣是正交矩陣，各個列向量都是單位向量，且兩兩正交，即

r₃＝r₁×r₂ (16)

則根據公式(15)，求解出旋轉矩陣的第一列列向量，第二列列向量，以及平移向量；根據公式(16)，將旋轉矩陣的第一列列向量和第二列列向量進行叉乘運算，得到旋轉矩陣的第三列列向量。

本發明提出的基于二次曲線透視投影不變性的單相機位姿估計方法直接在二次曲線方程的基礎上估計位姿，縮短了誤差的傳遞鏈，提高了位姿估計方法的穩健性；將求解由非線性方程組求解轉化成線性方程組求解，無需構造非線性目標優化函數去求解，且能夠在線性算法時間復雜度O(n)中完成。

附圖說明

圖1為本發明實施例提供的基于二次曲線透視投影不變性的單相機位姿估計方法流程圖；

圖2為本發明實施例提供的基于位姿估計的測棒快速標定裝置結構示意圖。

具體實施方式

為了便于理解本發明，下面將參照相關附圖對本發明進行更全面的描述。附圖中給出了本發明的較佳實施例。但是，本發明可以以許多不同的形式來實現，并不限于本文所描述的實施例。相反地，提供這些實施例的目的是使對本發明的公開內容理解的更加透徹全面。需要說明的是，當一個元件被認為是“連接”另一個元件，它可以是直接連接到另一個元件或者可能同時存在居中元件。除非另有定義，本文所使用的所有的技術和科學術語與屬于本發明的技術領域的技術人員通常理解的含義相同。本文中在本發明的說明書中所使用的術語只是為了描述具體的實施例的目的，不是旨在于限制本發明。本文所使用的術語“及/或”包括一個或多個相關的所列項目的任意的和所有的組合。

請參照圖1所示，圖1為本發明實施例提供的基于二次曲線透視投影不變性的單相機位姿估計方法流程圖。

本實施例中基于二次曲線透視投影不變性的單相機位姿估計方法具體包括如下步驟：

S101、根據二次曲線對應信息，估計相機成像平面和空間平面對象之間的單應性矩陣。

以圖2所示為例，相機201拍攝平面對象202上的圓形特征203。由于平面對象202可能不平行于成像平面，成像特征可能會是橢圓。在拍攝圖像中提取橢圓特征，從而得到的多組二次曲線對應信息。

基于二次曲線透視投影不變性，通過求解單應性矩陣，建立世界坐標系下單個二次曲線代數方程矩陣與對應相機坐標系下的二次曲線代數方程矩陣之間的轉換關系。

在計算機視覺中，單應性矩陣是用來描述從一個平面到另一個平面的投影映射，本實施中所述單應性矩陣指一個二維平面對象上的點與相機成像平面上的像點之間的映射關系；

相機的透視投影模型為：

其中，為相機坐標系下成像平面上點的齊次坐標，為世界坐標系下平面對象上點的齊次坐標；K是相機的內參數矩陣，其具體包括主點坐標、焦距參數，s為尺度因子；設[R t]為世界坐標系轉化到相機坐標系下的位姿參數；旋轉矩陣R可進行列向量的形式來表示，則：

[R t]＝[r₁ r₂ r₃ t] (2)

由于對象為平面物體，故則公式(1)表達為：

設H＝K[r₁ r₂ t]，公式(3)表達為

H即是世界坐標系平面與圖像平面的單應性映射；

平面內，二次曲線的代數方程可表示為：

Ax²+Bxy+Cy²+Dx+Ey+F＝0 (5)

使用矩陣的形式表達公式(5)，具體為：

根據公式(6)，平面對象上二次曲線上的點和二次曲線方程的關系表示為如下式：

根據二次曲線透視投影不變性，世界坐標系下二次曲線在成像平面上的透視投影成像也是二次曲線；同理，根據公式(7)，成像平面上二次曲線上的點和二次曲線方程的關系可以表示為如下式：

其中，C′表示成像平面二次曲線代數方程的矩陣參數；

將公式(4)帶入公式(8)，可得：

聯立公式(7)、(9)，得出世界坐標系內的二次曲線和成像平面內的二次曲線之間的關系，即：

C＝sH^TC'H (10)

不失一般性的，限定兩個矩陣行列式值得情況下，將(10)表達為：

C＝H^TC'H (11)

其中：det(H)＝1，det(C)＝1，det(C')＝1。

對于求解單應性矩陣H，公式(11)的求解是非線性的，而非線性方程的求解容易陷入局部最優解的誤區。

本實施例中聯立同一平面內兩組二次曲線對應性等式方程，將求解單應性矩陣方程由非線性方程轉化成線性方程求解，過程如下：

設空間有n個二次曲線C_i，i＝1,2,3....n，所有的空間二次曲線在一個平面上,其在成像平面上的對應的二次曲線為C_i'，i＝1,2,3....n，且空間的n個二次曲線在同一個世界坐標系下；對于兩組二次曲線對應信息，建立如下等式：

C_i^-1C_j＝H^-1C_i'^-1C_j'H (12)

由公式(12)可得，

C_i'^-1C_j'H-HC_i^-1C_j＝0 (13)

其可以轉化為線性方程：

M_ijh＝0 (14)

其中：h＝[H₁₁ H₂₁ H₃₁ H₁₂ H₂₂ H₃₂ H₁₃ H₂₃ H₃₃]^T，

設定

當二次曲線對應信息個數大于兩個時，公式(14)的求解應該歸結于超定線性方程組的求解；利用最小二乘方法得到單應性矩陣的最優解。

S102、根據所述單應性矩陣，求解出位姿參數中的旋轉矩陣和平移向量。

相機的內參數矩陣為K，單應性矩陣為H，則：

[r₁ r_2t]＝HK^-1 (15)

由于旋轉矩陣是正交矩陣，各個列向量都是單位向量，且兩兩正交，即

r₃＝r₁×r₂ (16)

則根據公式(15)，求解出旋轉矩陣的第一列列向量，第二列列向量，以及平移向量；根據公式(16)，將旋轉矩陣的第一列列向量和第二列列向量進行叉乘運算，得到旋轉矩陣的第三列列向量。

本發明的技術方案直接在二次曲線方程的基礎上估計位姿，縮短了誤差的傳遞鏈，提高了位姿估計方法的穩健性；將求解由非線性方程組求解轉化成線性方程組求解，無需構造非線性目標優化函數去求解，且能夠在線性算法時間復雜度O(n)中完成。

本領域普通技術人員可以理解實現上述實施例方法中的全部或部分流程，是可以通過計算機程序來指令相關的硬件來完成，所述的程序可存儲于一計算機可讀取存儲介質中，該程序在執行時，可包括如上述各方法的實施例的流程。其中，所述的存儲介質可為磁碟、光盤、只讀存儲記憶體(Read-Only Memory，ROM)或隨機存儲記憶體(Random Acces s Memory，RAM)等。

注意，上述僅為本發明的較佳實施例及所運用技術原理。本領域技術人員會理解，本發明不限于這里所述的特定實施例，對本領域技術人員來說能夠進行各種明顯的變化、重新調整和替代而不會脫離本發明的保護范圍。因此，雖然通過以上實施例對本發明進行了較為詳細的說明，但是本發明不僅僅限于以上實施例，在不脫離本發明構思的情況下，還可以包括更多其他等效實施例，而本發明的范圍由所附的權利要求范圍決定。