本發明屬于電力系統技術領域，具體涉及一種非平衡電力系統頻率估計方法。

背景技術：

在電力系統中，常用的頻率估計采用基于相位的方法，但此類方法不適用于發生大幅度的頻率震蕩的情況。

實際電力系統中由于存在諧波干擾、噪聲和非平衡電壓等無法預料的情況，在這些情況下對電力系統的頻率進行快速而又準確的估計具有很大的實用意義。

由于標準單相技術的局限性，特別是當所選相遭受電壓下降或瞬變時會嚴重影響頻率估計的準確性。考慮線間電壓時，由于在三相系統中存在六個不同的單相電壓，難以選擇最具代表性的單相信號來充分描述系統頻率。

比較好的解決方案是設計一個同時考慮所有三相電壓的框架，當任何相位遭受驟降，瞬變或諧波時可以對增強的魯棒性作出統一估計。為此，clarke變換根據所有三相電壓提供的信息構建了復信號，此變換使經典單相方法具有增強的魯棒性，并且在復域中開發了許多已被證明比在真實域中的相應方法更可靠的解決方案。這些解決方案包括使用鎖相環(pll)、最小二乘法、卡爾曼濾波和基于解調的方法。但是，在非平衡系統中這些解決方案往往不能滿足實際需求。

技術實現要素：

發明目的：針對現有技術中存在的問題，本發明公開了一種基于寬線性最小方差無失真響應的非平衡電力系統頻率估計方法，該方法更適用于非平衡系統。

技術方案：一種基于寬線性最小方差無失真響應的非平衡電力系統頻率估計方法，包括如下步驟：

步驟1、建立三相電力系統的復電壓信號：

其中va、vb、vc分別為三相電壓信號的峰值電壓，△t為采樣間隔，等于1/fs，fs為采樣頻率，φ為初始相位，ω＝2πf0為電壓信號的角頻率，f0為系統頻率；

步驟2、建立非平衡電力系統電壓信號的wl-mvdr譜：

其中f＝[1,0]^t，vaug(k)＝[v^t(k),v^h(k)]^t為復電壓信號v(k)的增廣向量，為復電壓信號v(k)的增廣協方差矩陣，其中r為協方差矩陣，c為偽協方差矩陣，對求逆得到矩陣g和d，為激勵矢量，s＝[1,e^-jω,…,e^-j(k-1)ω]^t，k為協方差矩陣r的維數；

符號t表示向量或矩陣的轉置；h表示矩陣的共軛轉置；符號*表示矩陣的伴隨矩陣；符號-1表示矩陣的逆矩陣；

步驟3、求解使代價函數最小的角頻率為系統角頻率的估計值

所述代價函數j(k)為：

系統頻率的估計值為：其中fs為采樣頻率。

優選地，步驟3中采用自適應算法計算系統角頻率的估計值步驟如下：

(2.1)確定迭代初始值ω(0)，構建角頻率ω更新模型：

ω(k+1)＝ω(k)-μ(coe1*sin(2ω(k))+coe2*cos(2ω(k))+coe3*sin(ω(k))+coe4*cos(ω(k)))

其中ω(k+1)表示第k次迭代估計的角頻率，μ為迭代步長，

re(·)表示取括號內數值的實部，im(·)表示取括號內數值的虛部；

f(ω)＝s^hgs，g(ω)＝s^td*s，

(2.2)迭代計算步驟(2.1)中的ω(k+1)，檢查本次迭代得到的角頻率是否滿足收斂條件，如滿足，則ω(k+1)即為系統角頻率的估計值

收斂條件為：|ω(k+1)-ω(k)|≤ε或迭代次數k達到預設迭代次數閾值l；ε是一個極小的正實數。

作為另一種優選，步驟3中采用直接求解法計算系統角頻率的估計值步驟如下：

(3.1)建立關于角頻率的一元四次方程：

其中

re(·)表示取括號內數值的實部，im(·)表示取括號內數值的虛部；

f(ω)＝s^hgs，g(ω)＝s^td^*s，

(3.2)求解步驟(3.1)中的一元四次方程，得到4個解，選擇其中最接近系統角頻率期望ω0＝2πf0/fs的作為系統角頻率的估計值f0為系統頻率期望；fs為采樣頻率。

上述計算中，矩陣g和d由增廣協方差矩陣求逆計算得到，具體步驟為：

(4.1)根據復電壓信號的觀測值，建立數據陣v(k)：

其中m為用于計算的有效觀測長度；n為總觀測長度；

(4.2)增廣協方差矩陣的逆可以由矩陣求逆引理得到：

(4.3)迭代計算步驟(4.2)中的檢查相鄰兩次迭代得到的是否滿足收斂條件，如滿足，則即為增廣協方差矩陣的逆矩陣；

(4.4)根據可得到協方差矩陣g和偽協方差矩陣d。

為了提高頻率估計的精度，計算出矩陣g和d后，對g和d進行系數補償：

g＝c1g′，d＝c2d′

其中c1和c2為補償系數，g′和d′為補償前的矩陣，g和d為補償后的矩陣。

優選地，c1＝2.859，c2＝1。

有益效果：與現有的技術相比，本發明具有以下優點：1.充分利用了三項電壓完整的二階信息，增強了頻率估計的魯棒性。2.與傳統的線性自適應估計相比，該方法更適用于非平衡系統并且給出了無偏的頻率估計。3.該模型對于三相電壓振幅隨時間的推移和高次諧波存在的變化也不敏感。4.充分考慮輸入信號與輸出信號的噪聲，魯棒抗噪性能好。5.算法穩定，計算復雜度低，收斂性能，穩態收斂精度均明顯高于同類其他算法。

附圖說明

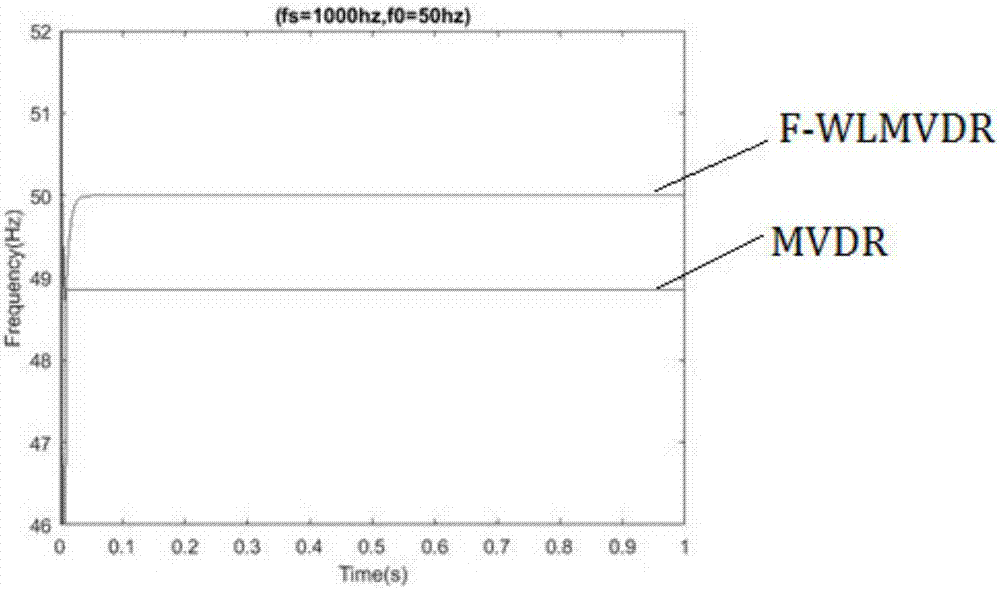
圖1為typeb型電壓暫降的非平衡系統下基于mvdr算法與基于wlmvdr算法的頻率估計對比圖；

圖2為步長與迭代的wl-mvdr算法估計均方誤差之間的關系；

圖3為typeb型電壓暫降的非平衡系統下，信噪比snr從20db到50db進行100次獨立重復試驗，基于mvdr算法與基于wlmvdr算法的頻率估計偏差對比圖；

圖4typeb型電壓暫降的非平衡系統下，信噪比snr從20db到50db進行100次獨立重復試驗，mvdr算法與wlmvdr算法的方差以及克拉美勞下界；

圖5為當電壓幅度調制情況下兩種算法的頻率估計；

圖6為當電壓頻率調制情況下兩種算法的頻率估計；

圖7為當添加諧波分量造成不平衡情況的頻率估計；

圖8為當va(k)變化造成真實數據不平衡情況的頻率估計圖；8(a)為真實數據相位a電壓變化的三相電壓圖；8(b)為真實數據相位a電壓變化時頻率估計圖。

具體實施方式

下面結合附圖和具體實施方式，進一步闡明本發明。

一種基于寬線性最小方差無失真響應的非平衡電力系統頻率估計方法，包括如下步驟：

步驟1、建立三相電力系統的復電壓信號；

對三相電力系統中的電壓信號進行采樣，得到三相電力系統電壓模型，可表示成下面的離散形式：

va(k)＝vacos(ωkδt+φ)z(1)

其中，va、vb、vc為峰值電壓，△t為采樣間隔，等于1/fs，這里fs為采樣頻率，φ為初始相位，ω＝2πf0為電壓信號的角頻率。

將三相電壓通過克拉克變換變換到二相靜止坐標系上，即與時間有關的三相電壓可以通過正交克拉克變換得到一個零序列v0和兩個相互垂直的分量vα、vβ，即：

其中，是用來確保變換中系統功率不變。

在沒有噪聲的平衡系統條件下，va、vb、vc是相等的，即：

其中幅度值是一個常數，vα(k)和vβ(k)是位置隨時間變化的速率正比于系統頻率的一個點的縱坐標。在實際中，通常只用vα和vβ部分來組成復電壓v(k)，即：

這里ω0＝ωδt，為歸一化角頻率，vα(k)和vβ(k)表示某一時刻電壓的正交表示。對于給定的采樣頻率fs，v(k)的概率密度函數是旋轉不變的，因為對于任意正的θ，v和ve^θ有著相同的分布。這意味著v(k)是一個二階圓信號，vα(k)和vβ(k)的能量相等，所以協方差矩陣r＝e[v(k)v(k)^h]能充分描述其二階統計特性，并且偽協方差矩陣c＝e[v(k)v(k)^t]＝0。

當三相電力系統偏離正常狀態，例如存在不同程度的凹陷或瞬變，va、vb、vc變得不相等，則復電壓信號為：

其中va、vb、vc分別為三相電壓信號的峰值電壓，△t為采樣間隔，等于1/fs，fs為采樣頻率，φ為初始相位，ω＝2πf0為電壓信號的角頻率，f0為系統頻率。

步驟2、建立非平衡電力系統電壓信號的wl-mvdr譜；

將復電壓信號v(k)分別通過兩個p階復數fir帶通濾波器后再合并為y(n)，則復電壓信號的功率為y(n)的功率除以濾波器帶寬。設兩個帶通濾波器的系數為：gi＝[gi(0),gi(1),…gi(p)]^h，i∈{1,2}；則：

其中，vaug(k)＝[v^t(k),v^h(k)]^t，

在約束條件

g^hs1＝1g^hs2＝0(9)

下，使得輸出功率最小的g的解為：

其中，s＝[s1,s2]，s1＝[s^t,0^t]^t，s2＝[0^t,s^h]^t，

s＝[1,e^-jω,…,e^-j(k-1)ω]^t(11)

為增廣協方差矩陣。

其中r為協方差矩陣，c為偽協方差矩陣。k為協方差矩陣r的維數。

對于非平衡系統，當v(k)由式(7)出時，可得：

同理可得：

±[v(k-1)v^*(k-1)]＝|a|²+|b|²(17)

所以，

同理，

可知協方差矩陣r為共軛對稱陣，矩陣c為對稱陣。

將代入輸出功率p，可得：

其中，f＝[1,0]^t,

由數學矩陣求逆規律可知，可表示為:

且矩陣g為共軛對稱陣，d為對稱陣。代入輸出功率p表達式可得wl-mvdr譜為：

其中f＝[1,0]^t，vaug(t)＝[v^t(k),vh(k)]^t為復電壓信號v(k)的增廣向量，為復電壓信號v(k)的增廣協方差矩陣，其中r為協方差矩陣，c為偽協方差矩陣，對求逆得到s為激勵矢量，s＝[1,e^-jω,…,e^-j(k-1)ω]^t，k為協方差矩陣r的維數；

步驟3、求解使代價函數最小的角頻率為系統角頻率的估計值

wl-mvdr譜在期望頻率f0處表現出一個峰值。

當s的基礎頻率ω和輸入信號中所包含的頻率分量(由協方差矩陣表示)一樣的時候，wl-mvdr估計算法返回該頻率分量處的能量。然而，在有噪聲的情況下，假設每個頻率分量處的能量都大于噪聲的能量，pwlmvdr的倒數在每一個頻率分量處有一個極小值。理論上，每一個極小值所在的位置都和實際存在的頻率分量相對應，其中，絕對值最小的極小值所在的位置為基頻分量。當只存在基頻和白噪聲的時候，協方差矩陣r的維數k＝2。

wl-mvdr頻率估計基于最小化代價函數j(k)：

可以采用自適應算法或直接求解法計算系統角頻率的估計值

采用自適應算法計算系統角頻率的估計值的步驟如下：

(2.1)確定迭代初始值ω(0)，構建角頻率ω更新模型；

使用lms(least-mean-square，最小均方)梯度：

其中μ為迭代步長，用來權衡收斂速度和估計精度。設：

f(ω)＝s^h5sg(ω)＝s^td^*s

于是，

所以：

而

所以，

其中，

角頻率ω更新模型為：

ω(k+1)＝ω(k)-μ(coe1*sin(2ω(k))+coe2*cos(2ω(k))+coe3*sin(ω(k))+coe4*cos(ω(k)))(35)

其中ω(k+1)表示第k次迭代估計的角頻率，re(·)表示取括號內數值的實部，im(·)表示取括號內數值的虛部；

(2.2)迭代計算步驟(2.1)中的ω(k+1)，檢查本次迭代得到的角頻率是否滿足收斂條件，如滿足，則ω(k+1)即為系統角頻率的估計值

收斂條件為：|ω(k+1)-ω(k)|≤ε或迭代次數k達到預設迭代次數閾值l；ε是一個極小的正實數。

采用直接求解法計算系統角頻率的估計值步驟如下：

(3.1)建立關于角頻率的一元四次方程；

在穩定的狀態下，式(35)收斂，梯度趨近于0，即：

coe1*sin(2ω)+coe2*cos(2ω)+coe3*sin(ω)+coe4*cos(ω)≈0(36)

由萬能公式：

以及二倍角公式：

sin(2ω)＝2sin(ω)cos(ω)cos(2ω)＝2cos²(ω)-1

式(35)可以化為：

其中coe1～coe4分別為式(31)～式(34)取ω＝ω0時的值，即：

(3.2)求解步驟(3.1)中關于的一元四次方程，得到的解x后，利用即可得到系統角頻率的估計值

由于一元四次方程有4個解，選擇使系統角頻率的估計值最接近系統角頻率期望ω0＝2πf0/fs的作為最終的系統角頻率的估計值f0為系統頻率期望；fs為采樣頻率。

計算出后，系統頻率的估計值為：其中fs為采樣頻率。

上述計算中，矩陣g和d由增廣協方差矩陣求逆計算得到，具體步驟為：

(4.1)根據復電壓信號的觀測值，建立數據陣v(k)：

其中m為用于計算的有效觀測長度；n為總觀測長度；

(4.2)增廣協方差矩陣的逆可以由矩陣求逆引理得到：

(4.3)迭代計算步驟(4.2)中的檢查相鄰兩次迭代得到的是否滿足收斂條件，如滿足，則即為增廣協方差矩陣的逆矩陣；

(4.4)根據可得到協方差矩陣g和偽協方差矩陣d。

由于對矩陣求逆的計算過程會影響到結果的精度，以γ＝0.7的typeb型非平衡電壓系統為例，采樣頻率為1000hz，將計算出來的與相乘，結果為：

計算結果與單位矩陣之間存在較大的誤差。為了解決這個問題，一種辦法是尋求更加精確的求逆算法，另一種辦法是對現有求逆算法進行補償，使得求逆后的矩陣與原矩陣的乘積盡可能地接近于單位陣i，即：

令g＝c1g′，d＝c2d′，其中c1和c2為補償系數，g′和d′為補償前的矩陣，g和d為補償后的矩陣。用補償后的矩陣g和d進行計算，即：

r(k)g+c(k)d^*＝i(40)

c^*(k)g+r^*(k)d^*＝o(41)

r(k)d+c(k)5^*＝o(42)

c^*(k)d+r^*(k)g^*＝i(43)

經過計算，c1＝2.859，c2＝1時計算結果的精度較高。

實施例1：

將估計頻率初始化為49.5hz，系統實際頻率為f0＝50hz，迭代的wl-mvdr算法的迭代步長設為μ＝0.1，估計結果如圖1所示。其中f-mvdr表示用mvdr算法進行的頻率估計，mvdr表示的是沒有迭代的mvdr頻率估計算法。由圖1可知，迭代的wl-mvdr算法都能精確地估計系統頻率，而mvdr算法有一定的偏差。

接下來考慮在有噪聲的情況下，兩種算法的估計偏差和方差的比較。

首先考察步長μ對迭代的wl-mvdr算法的影響。步長在自適應算法中對于最小化代價函數有著很重要的作用，步長越小，算法越穩定，收斂得越慢；反之，步長越大，算法穩態估計誤差越大，收斂得越快。圖2表明在信噪比snr＝50db電壓為typeb型下陷的情況下，不同的步長μ對迭代的wl-mvdr估計算法性能的影響，此處性能用均方誤差(mse)表示。由圖2可知，步長越小，均方誤差越小，估計越精確。

接下來，通過與估計方差的理論克拉美-勞(crlb)下界作比較，分析這兩種算法的估計方差。圖3和圖4表示的是不同的信噪比情況下，μ＝0.1時，100次獨立重復仿真后幾種算法的估計偏差和方差的比較。其中f-mvdr表示用mvdr算法進行的頻率估計，f-wlmvdr表示用wl-mvdr算法進行的頻率估計。結果表明，在信噪比很大的情況下，迭代的wl-mvdr算法表現出了無偏性，而mvdr算法有一定的偏差。這與理論相符。在方差分析圖中，wl-mvdr算法比i-mvdr算法更接近于crlb下界，估計性能較好。

然后討論當typeb型下陷的電力系統中調幅的情況下的算法性能，(無噪聲)即：

va(k)＝1+0.05sin(2πkδt)

va(k)＝1+0.1sin(2πkδt)

va(k)＝1+0.15sin(2πkδt)

仿真結果如圖5，該圖表明，在一點調幅的情況下wl-mvdr表現出了很小的估計誤差，而mvdr算法振蕩相對比較大。

snr＝50db的條件下，假設系統頻率在某一時刻突然改變，考察集中算法的跟蹤性能及反應。即設：

圖6表明兩種算法對于頻率變化的跟蹤情況，由該圖可以看出，迭代的wl-mvdr算法與f0最為接近，跟蹤效果最好，反應最快；i-mvdr算法估計誤差較大。

最后考慮高階諧波對集中估計算法的性能影響。仍然取typeb型電壓下陷，snr＝50db加上20％的3階諧波、10％的5階諧波以及10％的7階諧波，加入了諧波之后的電壓和電壓跟蹤結果如圖7，可以清楚地看出迭代的wl-mvdr算法在高階諧波的干擾下估計更加穩定精確。

實施例2：

將該方案用于真實環境中進行頻率估計。實際中，三相電壓由一個110/20/10kv的變壓站記錄。由abb公司生產的rel531數字線路距離保護終端被安裝在站內，用于監測三個“相-地”電壓的變化。該設備被用來為記錄每當相電壓值下降到其正常值的90％以上超過20ms的情況。在1khz下對系統頻率為50hz的測量的三個“相—地”電壓進行采用，如圖8(a)所示，在t＝0.06s附近，相位va與地短路，電壓下降到其正常值的44％。同時，相位vb和vc電壓分別驟升36％，50％，得到的非圓度γ＝0.0448。

wl-mvdr算法與mvdr算法頻率估計能力分別如圖8(b)所示，wl-mvdr算法在正常操作條件下提供了準確的響應，然而，mvdr算法處理不平衡的能力較差。