一種預測公交車到站時間的方法與流程
本發明涉及交通技術領域,更具體地,涉及預測公交車到站時間的方法。
背景技術:
隨著我國城市化進程的發展,城市的經濟得到了發展,人口、車輛也大量增加,隨之引發了一系列的交通問題,尤其是交通擁堵。公共交通具有承載率高、污染小、運輸效率高等特點,故大力發展公共交通可以減緩城市擁堵現象。近年來,智能交通得到了重視和發展,出行者對于公交車到站時間的獲取需求也日益增加。到站時間公開之后,乘客可以提前規劃行程。這將吸引他們選擇公共交通出行,從而緩解交通壓力。此外,公交運營公司的可以根據公交車的到站時間進行調度,有利于公交管理向動態智能化的轉變,提高運營效率。
公交到站時間預測近年來在國內外都引起了廣泛關注。例如,都柏林在站點設置了電子站牌來展示到站時間;在日本,公交車到達時間預測是政府大力支持的一項交通需求管理措施。通過互聯網向用戶的手機和電腦發送公交車的預測到達時間吸引人們乘坐公交車出行,從而限制私家車使用數量。在中國的應用主要分為兩種:一種是布置實體公交電子站牌,例如上海在站牌上展示公交到站時間;另外一種是利用客戶端軟件發布信息。用戶可以通過這些軟件獲取公交車的位置(距離)信息等。
目前雖然存在多種預測模型,如基于歷史數據、人工神經網絡、支持向量機等,但是基本上預測精度有限。公交車的行駛過程受到各種隨機因素的影響,尤其我國城市交通環境復雜,目前已有的成熟預測方法得到的公交到站時間不夠準確,可靠性較低。總體看來,關于公交車到達時間預測技術的研究仍然較少或者存在一定的局限性,亟待開發一種新型的公交到站時間預測方法。
技術實現要素:
本發明提供一種克服上述問題或者至少部分地解決上述問題的預測公交車到站時間的方法。
根據本發明的一個方面,提供一種預測公交車到站時間的方法,其特征在于,包括:
S1、采集一定時間內的公交車數據以及公交線路數據,基于空間插值法,獲得公交車在各數據點的時距數據對;
S2、基于所述時距數據對,獲得公交車運營序列;
S3、將所述公交車運營序列輸入至LSTM遞歸神經網絡,獲得公交車到站時間預測模型;以及
S4、對所述公交車到站時間預測模型基于鏈式預測法,獲得預測的公交車到站時間。
本發明提出利用遞歸神經網絡進行公交到站時間預測的方法:利用我國城市公交在運營時的公交車數據和公交線路數據,提取與交通相關的信息,經過訓練LSTM遞歸神經網絡,學習交通狀況變化的規律,從而得到公交車在動態變化交通環境下的到站時間。
附圖說明
圖1為本發明實施例中LSTM型RNN中隱藏層結點的結構圖;
圖2為根據本發明實施例的預測公交車到站時間的流程示意圖;
圖3為根據本發明實施例的計算除首站之外站點的出發時間的一維線性回歸示意圖;
圖4為根據本發明實施例的預測到站時間結果說明圖;
圖5為根據本發明實施例的預測方法與其他4種方法的結構圖。
具體實施方式
下面結合附圖和實施例,對本發明的具體實施方式作進一步詳細描述。以下實施例用于說明本發明,但不用來限制本發明的范圍。
為了克服現有預測方法存在的公交到站時間不夠準確、可靠性交底的計算問題,本發明提供了一種基于LSTM遞歸神經網絡的預測公交車到站時間的方法。下面結合附圖對本發明的具體實施方式進行說明。
遞歸神經網絡(Recurrent Neural Network,RNN)通過添加自連接隱藏層,賦予神經網絡對時間進行建模的能力,從而區別于其他的神經網絡。RNN隱藏層的輸出,不僅僅會傳播到下一層,而且還進入了下一時刻的本隱藏層,但RNN會受到梯度消失或梯度爆炸的影響,導致它難以學習較遠時間點對當前時間點的影響。本發明采用具有解決上下文長時間依賴的RNN網絡結構,如長短時神經網絡(Long Short Term Memory,LSTM),帶門結構的遞歸單元神經網絡(Gated Recurrent Unit,GRU)等。
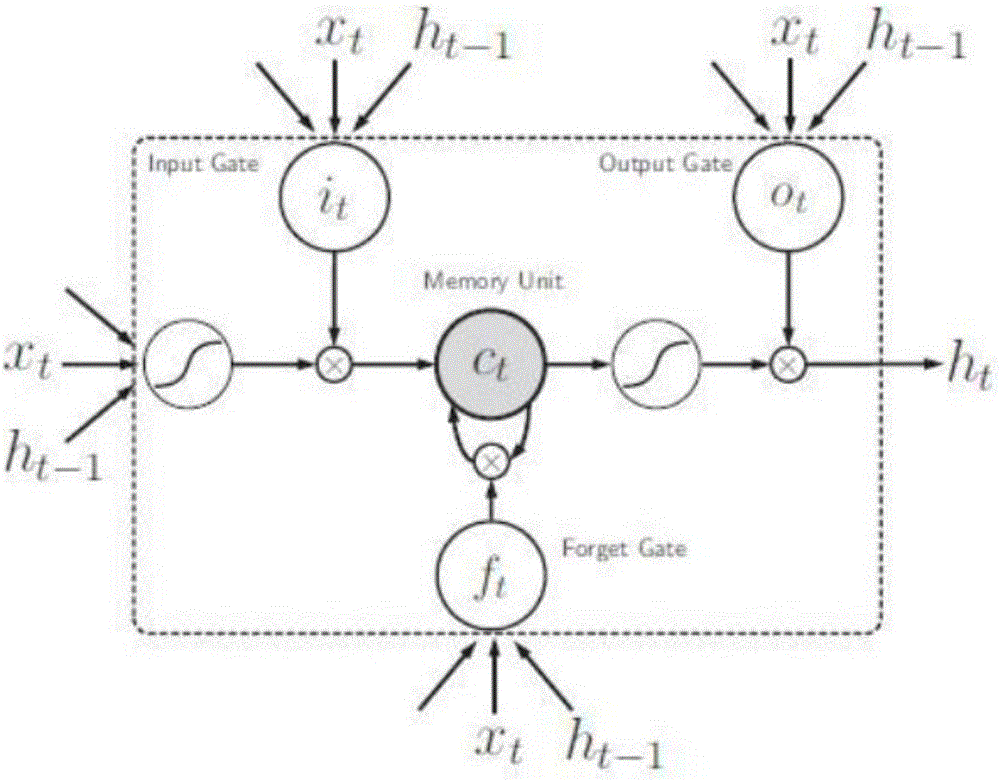
本發明采用的RNN為LSTM型RNN,通過將普通的神經元用帶有門結構(在本發明中,包括輸入門、遺忘門和輸出門)的記憶單元(Memory Cell)替換,解決了梯度消失或梯度爆炸的問題。在前向傳播中,門結構控制了激活的進入和輸出;在后向傳播中,門結構控制了殘差的流入和流出。如圖1所示,此為帶有一個記憶單元的隱藏層神經元結點,包含三個門:輸入門i、遺忘門f和輸出門O,it,ft,ot分別是三個門在時刻t對應的激活值;xt和ht-1是神經元輸入數據的兩個來源,其中xt是上一層的神經元在t時刻的輸出,而ht-1是上一個時刻即t-1時刻本層所有神經元的輸出值;Ct是內部狀態在此時刻的值;ht是當前t時刻隱藏結點的輸出值。它們的計算過程為:
it=σ(Wxi*xt+Whi*ht-1+bi);
ft=σ(Wxf*xt+Whf*ht-1+bf);
ot=σ(Wxo*xt+Who*ht-1+bo);
Ct=ftοht-1+itοgt;
其中Wxg,Wxi,Wxf,Wxo,Whg,Whf分別是連接各層(不同結構)的邊的權值;bi,bf,bo,bg是偏置項,權值和偏置項都是待求參數。在RNN中,權值和偏置項在不同的時刻共享相同的值。σ和是不同的激活函數,σ常為Sigmoid函數,而可以為tanh函數或tanh函數的變種。ο運算符代表元素對應相乘。
利用LSTM能夠學習長期依賴關系的特點,本發明從已有的定位數據和靜態數據中提取在公交到站預測問題中LSTM所需的時間序列信息,用這些信息反映描述某時間某位置的交通狀況。本發明將時間序列信息輸入至網絡中以學習交通狀態,并用LSTM記憶單元的內部狀態進行存儲。隱藏層節點的輸出經過前向傳播過程,直到網絡的輸出層,通過預測到站時間。故本發明預測的公交到站時間是基于動態變化的交通狀態的,更具有可靠性。
圖2示出了本發明的流程示意圖,包括:
S1、采集一定時間內的公交車數據以及公交線路數據,基于空間插值法,獲得公交車在各數據點的時距數據對;
S2、基于所述時距數據對,獲得公交車運營序列;
S3、將所述公交車運營序列輸入至LSTM遞歸神經網絡,獲得公交車到站時間預測模型;以及
S4、對所述公交車到站時間預測模型基于鏈式預測法,獲得預測的公交車到站時間。
本發明提出利用遞歸神經網絡進行公交到站時間預測的方法:利用我國城市公交在運營時的公交車數據和公交線路數據,提取與交通相關的信息,經過訓練LSTM遞歸神經網絡,學習交通狀況變化的規律,從而得到公交車在動態變化交通環境下的到站時間。
本發明所述的公交車數據包括:公交車編號、公交車所屬線路的線路編號、公交車的地理位置數據、公交車的地理位置數據的采集時間、運營次數以及上下行方向,其中公交車的地理位置數據為公交車在運營過程中通過車載定位系統發射的全球定位系統(Global Positioning System,GPS)數據。
本發明所述的公交線路數據包括:公交線路的線路編號、線路中各站點編號、各站點的地理位置數據、各路口的地理位置信息以及上下行方向。之所以選擇路口,是因為交通受到信號燈的控制影響較大,主要體現在信號燈的改變會引發交通狀態的突然變化,從而影響公交車的運行時間,比如由綠燈變換成紅燈之后,交通流被截斷,處于被截斷部分交通流的公交車會增加停車延誤時間以及引道延誤時間。
由于公交線路數據和公交車數據通常保存在公交公司的數據庫中,數據的組織形式是雜亂無章的,本發明首先需要將屬于公交車不同次運營的定位數據區分開來,使每一個劃分出來的小集合里的數據都屬于同一次運營。
具體地說,所述步驟S1包括:
S1.1、采集一定時間內的公交車數據以及公交線路數據,獲得對應不同線路、不同運營次數的公交車的歷史時距數據信息,所述歷史時距數據信息包括所述線路的首站點和末站點的地理位置數據、線路總距離和總到站時間。
獲得公交車的歷史時距數據信息的方法屬于現有技術,例如,可以采用專利“一種公交時距數據的獲取方法及服務器”(發明號:2016108876465)的方法獲得,
在到站預測問題中,我們還需要知道公交車到達各個站點的時間,因此,步驟S1還包括步驟S1.2:基于所述歷史時距數據信息,通過空間插值法,獲得各數據點的積累距離。
所述步驟S1.2具體包括:根據線路編號和上下行標志,我們從數據表里查詢線路的中間站點和沿線路的路口的經緯度位置。通過空間插值,如克里金插值法得到站點(也可以是路口,下同)的累積距離:設某次運營的定位數據的坐標值為x1,x2,...,xn,對應的觀測值為計算得到的累積距離Z(x1),Z(x2),...,Z(xn),所述積累距離為該站點到首站點的距離,那么對于某個站點(路口)的經緯度坐標x0,它對應的累積距離Z(x0)可以用線性組合來估計,其中λi為組合權重,體現了x0與x1,x2,...,xn之間的關系,該關系通過求解克里金方程得到,由于篇幅問題,求解克里金方程的方法不再詳細說明,可參考論文Oliver,M.A."Kriging:A Method of Interpolation for Geographical Information Systems."International Journal of Geographic Information Systems 4:313–332.1990。
在得到中間站點的累積距離之后,我們通過線性回歸的方法計算公交車的到達除首站之外各站點的時間。根據已知的輸入,輸出數據(在該問題中,輸入和輸出分別為定位數據的連續累積距離和采集時間),擬合線性函數(在該問題中,為連續累積距離和采集時間的關系表示),并將未知的數據輸入(在該問題中,為站點的累積距離)至擬合的函數中,得到所需要的值(在該問題中,為到達站點的時間)。具體的操作過程如下:
圖3示出了計算各站到達時間的線性回歸示意圖,如圖3所示,黑色的點表示的是根據專利“一種公交時距數據的獲取方法及服務器”(發明號:2016108876465)獲得的各定位數據的連續累積距離以及采集時間,藍色的線是擬合函數,該擬合函數的過程通過python計算機程序語言中的sklearn.linear_model包來實現,具體的程序如下:
regr=linear_model.LinearRegression()
regr.fit(X,Y)
y_pred=regr.predict(x)
其中,第一個語句得到函數句柄,第二個語句輸入已知的輸入數據X和輸出數據Y,得到擬合函數;第三個語句輸入數據X至擬合函數中,計算得到y_pred,其中輸入數據X對應于公交車輛實時動態位置對應的累積距離;輸出數據Y對應于公交車輛實時動態位置所在的數據采集絕對時間,x是除去首站之外的各站點的累積距離,得到的y_pred即所需的各站到達時間。
進一步地,由于公交車在30秒時間間隔內的運營距離會較長,本發明對每百米距離的位置進行采樣,作為采樣點,通過線性插值,得到對應的公交車運行時間。
插值的目的是為了改善車載定位裝置低頻率發射定位數據的缺點,使模型能夠以更高頻率監測交通狀態的變化和公交車的運行情況。
在得到各數據點的積累距離后,本發明的步驟S1還包括步驟S1.3,將所述積累距離和對應的到站時間作為公交車到達該數據點時的時距數據對。
在一個實施例中,時距數據對相應的來源可能是站點、采樣點或者路口點。一次運營過程中,按時間順序排列的所有時距數據對記錄了公交車在時間和空間范圍內的移動情況。
在一個實施例中,本發明在獲得所有時距數據對后,開始構建時間序列,以訓練LSTM模型,在公交車到站時間預測問題中,公交車運營序列(或簡稱為運營序列)是“時間序列”。
本發明中的所述步驟S2具體包括:
S2.1、將公交車到達各數據點時的時距數據對、當前數據點與下一數據點的間距、共享同一個站點的線路總數以及數據標識符作為特征向量,構成對應各數據點的公交車運營特征向量。
具體來說,一次運營中的所有時距數據對的序列記為S=(S1,S2,...,Si,...SN),其中Si=(ti,di)T,記錄了公交車到達Si對應位置的運行時間ti和積累距離di。以Si為例,計算LSTM所需的部分輸入信息,包括:當前時刻Ti=ti+ST,其中,ST是公交車離開第一個站點的絕對時間,當前位置和首站之前的距離以及和下一個數據點的間隔距離Δdi=di+1-di。
通過對數據庫的查詢得到共享同一個站點的線路總數量(li,當第i個數據點不對應站點時,值為0);給予每一個數據點一個one-hot向量(fi,即一位有效編碼)以區分不同來源的數據點,如:當數據點為站點時,fi=[0,0,1];當為采樣點時,fi=[0,1,0];當為公交車的地理位置時fi=[1,0,0]。這五種特征構成了一個公交時距數據對的運營特征向量,Xi=(Ti,di,Δdi,li,fi)T。
由此可知,運營特征向量的每個特征都是和交通狀態密切相關的:Ti和di分別為當前時刻(用絕對時間表示)和公交車所處的當前位置(用和首站之間的距離表示),這將告訴網絡需要學習何時何地的交通狀態;Δdi是待預測位置和當前位置之間的距離,這明確了需要預測多遠距離內的交通變化情況;li特指共享站點的線路數量,用來反映站點的承載力對公交車運營的影響:線路數量的多少關系到上進出站的排隊長度,從而影響上下車的延誤時間。在這樣的輸入條件下,本發明讓LSTM網絡學習在某時空條件限定下的交通狀態以及在一定距離范圍內交通的逐漸變化情況。在此期間若遇到信號燈路口等特殊位置,網絡還需要考慮交通突然變化的可能性。
運營序列作為LSTM的輸入,它對應的目標輸出是公交車到達下一個位置點的運行時間,即對Xi來說,對應的目標輸出Yi=ti+1。目標序列記為Y=(Y1,Y2,...,Yi,...YN-1)。線路所有的運營序列(X1,X2,...,XM)和對應的目標序列(Y1,Y2,...,YM)構成運營序列訓練集,其中M是此線路公交車運營的總次數。
在獲得公交車運營特征向量后,所述步驟S2進一步包括步驟S2.2:對所述公交車運營特征向量中除數據標識符外的各特征向量依次進行歸一化處理(除以各特征的最大值maxV)和去均值處理(減去各特征的均值meanV),獲得所述公交車運營序列。
在一個實施例中,所述步驟S3進一步包括:
基于所述公交車運營特征向量的維度,對所述公交車運營序列進行分批,獲得若干批數據。
具體地說,LSTM的輸入為K維向量,K即公交運營序列特征向量的維度(即特征向量的長度)。本發明將公交車運營序列進行分批:設定一個miniBatch值,例如可設定為256,將運營序列訓練集共分為(M/miniBatch)批。
對每一批數據來說,在公交車到達每一個數據點的時刻向LSTM遞歸神經網絡輸入該批數據對應的公交運營序列(miniBatch×K×1的矩陣),經前向傳播,所述LSTM遞歸神經網絡存儲交通狀態,并輸出網絡輸出值。
接下來比較所述網絡輸出值和此時刻的目標輸出值,獲得均方誤差,作為LSTM網絡的誤差,同時使用時間展開的后向傳播計算并傳遞殘差,對所有批的數據完成一次前向和后向傳播的過程稱為一次迭代,經多次迭代(可以預先設定一個值,也可以當誤差小于某個設定的值后停止迭代),獲得所述公交車到站時間預測模型。
在一個實施例中,基于隨機梯度下降法(Stochastic gradient descent,SGD),對LSTM遞歸神經網絡中的權值和偏置進行更新。具體的更新方程為:
new Wxi=Wxi+(m*Wxi-αΔWxi)
new bi=bi+(m*bi-αΔbi)
其余的權重和偏置的更新方程與上述公式類似。其中α是學習率,m是沖量因子,它的引入有助于訓練過程中更新的權重和偏置陷入局部最小值。
在本發明中,預測公交車到站時間的過程定義為“無輸入的鏈式預測”,所述步驟S4包括:
S4.1、將公交車的當前位置到預測位置之間的其他數據點作為輔助點。具體地說,假設線路共有n個站點,公交車當前正位于第i個站點(記為當前站點,i=1,...,n-1),想要預測到達下游目標站點(記為第j個站點,j=i+1,...,n)的時間。預測過程按照i->ap1->...->apn->j的順序展開,其中ap1,...,apn是兩個站點之間存在其他的位置點(如兩個站點之間的采樣點、路口點),我們將它們統稱為輔助點。
S4.2、向所述公交車到站時間預測模型輸入基于當前位置計算的公交車運營特征向量,經前向傳播獲得公交車運行至第一個輔助點的預測的到站時間。具體地說,根據當前站點的時距數據對Si計算對應的運營特征向量Xi,輸入至訓練好的LSTM網絡中,經過前向傳播過程得到的輸出值,即網絡預測公交車運行至ap1的時間,記為Op1。
我們繼續預測公交車從ap1運行至ap2的時間,由于車輛還未到達ap1所處的位置,所以,ap1對應的運營特征向量中的時間特征需要用上一步的預測結果來替代,即ap1對應的運營特征向量Xp1=(Tp1Dp1,Δdp1,lp1,fp1)T=(Op1,Dp1,Δdp1,lp1,fp1)T(除了當前時刻特征是用上一步的預測結果替換之外,其余特征都跟網絡輸出結果無關,可以從數據庫查詢得到或者計算得到)。
S4.3、將所述預測的到站時間將作為下一輔助點對應的到站時間,結合其余特征向量,構成下一輔助點的公交車運營特征向量,重復步驟S4.2,直至獲得預測位置的網絡輸出值;以及
S4.4、對所述步驟S4.3的網絡輸出值進行反去均值(加上S2.2步驟中得到的各特征的平均值meanV)和反歸一化(乘以S2.2步驟中得到的各特征的最大值maxV)處理,獲得預測的公交車到站時間。
當車輛位于第i個站點,下游的交通狀態都是預測得到的。隨著車輛的向前移動,如真正到達第i+1個站點后,我們才可以得到真實的運營特征向量。將該向量再輸入至LSTM網絡中糾正歷史預測的交通狀態,再次預測第i+1個站點的下游目標站點到站時間(這里的時間指當前時間減去公交車離開首站的時間得到的時間)。因此,對一次運營來說,預測結果是一個下三角矩陣,如圖5所示,橫坐標(水平方向)代表當前站點,縱坐標代表下游站點,則第列的含義代表公交車當前位于第個站點時預測到達下游各站點的時間。所以,圖4的矩陣包括以下含義,1、此線路共有十個站點;2、矩陣第t列(1≤t≤9)的含義為:當公交車到達第t個站點時,模型預測公交車到達第t+1個站點至第十個站點的時間。
下面給出本發明的的應用實例:
以北京118路(紫竹院南門—紅廟路口東)為例用本發明進行預測,并和其他方法進行比較。對比的方法是Sinn,M.,Ji,W.Y.,Calabrese,F.,&Bouillet,E.(2012).Predicting arrival times of buses using real-time GPS measurements.(Vol.24,pp.1227-1232)。對比文件中提到的四種方法,分別為:基于延遲的預測(,Delay-based Prediction,DB),線性回歸(Linear Regression,LR),K近鄰(K-Nearest Neighbor,KNN)和核回歸(Kernel Regression,KR)。
以在2015年2月份采集的該線路的定位數據為基礎進行到站時間預測。將前27天的數據(共704條公交車運營序列)作為訓練數據,預測2月28日共Y(Y=31)次運營的到站時間。并用平均絕對誤差(mean absolute error,MAE)評估預測結果:
我們使用的LSTM模型包含一個輸入層,一個共有64個隱藏節點的隱藏層以及一個單一的線性輸出單元。記憶單元的激活函數為tanh函數。值域在[0,1]之間的sigmoid函數是三個門的激活函數。權值用高斯分布進行初始化,使其服從N(0,1/(Nin+Nout),其中Nin和Nout分別指前一層和當前層的神經元數量。SGD方法的沖量因子設置為0.95,學習率在迭代中保持不變為0.0001。
五種方法得到結果如圖5所示。對所有預測長度的平均誤差而言,LSTM方法比其余四種方法中的最好結果提高了約24秒。在現實生活中,公交線路所在的道路上一般不會只有一輛公交車,所以短距離的預測是更貼近現實的。我們統計短距離預測的預測結果,預測距離為一站到五站,對應圖5的第三到第七行。當預測距離為一站時,預測公交車到達下一個站點的時間;當預測距離為兩站時,預測公交車到達下游兩個站點的時間,依此類推。注意,預測距離為所有站點時,則是預測公交車到達所有下游站點的時間。可以看到,LSTM的無論是長距離預測還是短距離預測,結果都是優于其他方法的。
綜上所述,本發明提供了一種利用遞歸神經網絡預測公交到站時間的方法。利用RNN來學習交通狀態的變化,將公交到站時間和交通情況關聯起來,得到更為可靠精確的預測結果。總的來說,用LSTM型RNN預測公交車到站時間具有以下的特點:
1.LSTM模型具有長時記憶歷史信息的優點。因為交通的變化也具有歷史相關性,上下游的交通情況是互相影響的,故我們用記憶單元來存儲交通狀態,并且利用記憶單元的內部狀態隨時間展開而變化的模式來模擬交通狀態的演變。LSTM網絡的輸出在本問題中定義為預測的到站時間,故得到的公交到站時間是基于交通狀態的,相對于其它方法是更值得信任的。
2.LSTM模型具有很好的擴展性。對于其他模型來說,加入多元信息很困難,而我們可以不斷地加入更多和交通相關的特征到LSTM模型中。在目前已有數據的基礎上我們只提取了五類特征。然而,交通還受到很多其他動態因素的影響,如天氣等。如果在未來能得到更多的信息,我們需要做的只是對數據進行處理得到新的特征,并增加LSTM網絡的輸入或者輸出維度。更多重要影響因素的加入可能會進一步提高預測的準確性。
3.LSTM模型不用限制序列的長度,故我們可將到站預測擴展為預測任意地點的公交車到達時間(適用于某些城市揮手即停的模式)。我們只需要對任意想要預測的位置進行插值,經過計算得到對應的運營特征向量,加入已有的序列中,再利用訓練好的模型進行鏈式預測即可。
最后,本發明的方法僅為較佳的實施方案,并非用于限定本發明的保護范圍。凡在本發明的精神和原則之內,所作的任何修改、等同替換、改進等,均應包含在本發明的保護范圍之內。
- 還沒有人留言評論。精彩留言會獲得點贊!