本發明屬于電動汽車電機調速控制技術領域，尤其涉及一種基于極限學習機的電動汽車異步電機驅動系統控制方法。

背景技術：

國際金融危機以來，美、歐、日、韓等發達國家都在推動汽車產業的轉型發展,全球范圍內形成了發展新能源汽車的又一輪熱潮。在所有技術創新中，電機驅動具有極其重要的地位,因為未來的驅動方式必須具有能耗低、更環保、更具有可持續性等特點。

電動汽車包括電機驅動及控制系統、驅動力傳動等機械系統和完成既定任務的工作裝置等。電機驅動及控制系統是電動汽車的核心，也是區別于內燃機汽車的最大不同點。電動汽車是汽車工業的一個重要分支，電動汽車的發展對于能源安全以及環境保護有著重大的意義。近年來，對于電動汽車的關注日益增高，與此同時，對高效、可靠、經濟的電機驅動技術的需求也日益緊迫。因此，電動汽車動力系統的研究受到了國內外學者的廣泛關注。

由于異步電機的動態數學模型具有高度的非線性、強耦合、多變量的特點，因此在電動汽車上異步電機需要一套更復雜的控制方法。為滿足實際應用對于電動汽車更高的要求，提出了模糊邏輯控制、反步法控制和滑模控制等基于最近現代控制理論的控制策略。所有的這些方法都假定可以得到動態系統方程。反步法是一種控制具有不確定性、非線性的系統，尤其是那些不滿足給定條件的系統的方法。反步法最大的優點是可以用虛擬控制變量簡化原始的高階系統，從而最終的輸出結果可以通過合適的Lyapunov方程來自動的得到。然而，傳統反步控制中對虛擬控制函數進行連續求導，容易引起“計算爆炸”問題。在控制不確定非線性系統，尤其是那些不滿足特定條件的系統方面，反步控制方法被認為是最常用的控制方法之一。這種控制設計的優點是使用虛擬控制變量來使原來的高階系統簡單化；與此同時，通過選擇一個合適的Lyapunov函數，可以系統地得到控制輸出。然而，傳統反步控制中對虛擬控制函數進行連續求導，容易引起“計算爆炸”問題。

極限學習機(extreme learning machine，簡稱ELM)是一種簡單易用、有效的單隱層前饋神經網絡SLFNs學習算法。傳統的神經網絡學習算法(如BP算法)需要人為設置大量的網絡訓練參數，并且很容易產生局部最優解。極限學習機只需要設置網絡的隱層節點個數，在算法執行過程中不需要調整網絡的輸入權值以及隱元的偏置，并且產生唯一的最優解，因此具有學習速度快且泛化性能好的優點。ELM因其在處理未知非線性函數方面的能力而廣泛的應用于具有高度非線性和不確定性的復雜控制系統設計中。

技術實現要素：

本發明的目的在于提出一種基于極限學習機的電動汽車異步電機驅動系統控制方法；該控制方法通過引入命令濾波技術，使用極限學習機算法來逼近未知的非線性項，應用自適應反步法技術使跟蹤誤差能夠收斂到原點的一個充分小的鄰域內，能夠有效地解決在參數不確定和有負載擾動的情況下考慮鐵損的異步電機的速度跟蹤控制的問題。

為了實現上述目的，本發明采用如下技術方案：

基于極限學習機的電動汽車異步電機驅動系統控制方法，包括如下步驟：

a建立考慮鐵損的異步電機的動態數學模型：

其中，ω_r表示考慮鐵損的異步電機轉子角速度；J表示轉動慣量；T_L表示負載轉矩；ψ_d表示轉子磁鏈；n_p表示極對數；i_qs,i_ds表示d-q軸定子電流；u_qs,u_ds表示異步電機d-q軸定子電壓；L_m表示互感；L_1r,L_1s分別表示定轉子漏感；R_s,R_r,R_fe分別表示異步電機定、轉子及鐵損等效電阻；i_qm,i_dm分別表示d-q軸勵磁電流；i_qs,i_ds分別表示d-q軸定子電流；

為簡化考慮鐵損的異步電機的動態數學模型，定義新的變量：

則考慮鐵損的異步電機的動態數學模型表示為：

其中，

b根據命令濾波技術和自適應反步法原理，設計一種基于極限學習機的電動汽車異步電機驅動系統控制方法；

考慮鐵損的異步電機的動態數學模型簡化為兩個獨立的子系統，即由狀態變量x₁，x₂，x₃和控制輸入u_qs組成的子系統以及由狀態變量x₄，x₅,x₆和控制輸入u_ds組成的子系統；

定義命令濾波器為：

其中，均為命令濾波器的輸出信號，α_u為命令濾波器的輸入信號，u＝1,2,4,5；如果輸入信號α_u對于所有的t≥0，使得以及成立，其中，ρ₁和ρ₂均為正常數；同時則可得出，對任意的常數μ＞0，存在ω_n＞0且ζ∈(0,1]，使得和是有界的；

定義跟蹤誤差變量為：

定義x_d為期望的位置信號；虛擬控制信號α₁,α₂,α₄,α₅為命令濾波器的輸入信號；x₁,_c,x_2,c,x_3,c,x_4,c,x_5,c為命令濾波器的輸出信號；k_g為正的設計參數；β_g是極限學習機算法的輸出權值向量，||β_g||是β_g的范數；H_g(Z_g)＝[G₁(a₁,b₁,Z₁),G₂(a₂,b₂,Z₂),...,G_g(a_g,b_g,Z_g)]，其中H_g(Z_g)表示極限學習機算法的隱層映射矩陣，G_g(·)是激活函數，在大多數應用中，為了簡單起見，對所有隱層節點使用的激活函數相同，(a_g,b_g)是隱層節點參數，Z_g是映射矩陣H_g(Z_g)的變量集合；l_g為正常數，g＝1,2,...,6是隱層神經元數。

控制方法的設計每一步都會選取一個合適的Lyapunov函數構建一個虛擬控制信號或者真實的控制律；控制方法的設計具體包括以下步驟：

b.1根據微分方程對z₁求導得誤差動態方程：定義命令濾波補償后的跟蹤誤差信號為：v₁＝z₁-ξ₁，同時選取Lyapunov函數：對V₁求導得：

在實際系統中負載參數T_L是有界的，定義T_L是未知的正常數且上限為d，即0≤T_L≤d；根據楊氏不等式可得：

其中，f₁＝a₁x₂x₄-x₂；對于光滑函數f₁(Z₁)，給定ε₁≥0，有極限學習機算法H₁β₁；令f₁(Z₁)＝H₁(Z₁)β₁+δ₁(Z₁)，δ₁(Z₁)表示逼近誤差，并滿足|δ₁(Z₁)|≤ε₁，從而有：

構建虛擬控制信號α₁為：

定義補償誤差

其中ξ(0)＝0，||ξ_g||是有界的，有μ＞0，ρ＞0，k_g為正的設計參數，g＝1,2,...6；

按照公式(5)、(6)和(7)將公式(4)改寫為：

b.2根據微分方程對z₂求導得誤差動態方程：定義命令濾波補償后的跟蹤誤差信號為：v₂＝z₂-ξ₂，同時選擇Lyapunov函數：

對V₂求導得：

其中，對于光滑函數f₂(Z₂)，給定ε₂≥0，有極限學習機算法H₂β₂；令f₂(Z₂)＝H₂(Z₂)β₂+δ₂(Z₂)，其中，δ₂(Z₂)表示逼近誤差，并滿足|δ₂(Z₂)|≤ε₂，從而有：

構建虛擬控制信號α₂：

定義補償誤差

按照公式(10)、(11)和(12)將公式(9)改寫為：

b.3根據微分方程對z₃求導可得誤差動態方程：定義命令濾波補償后的跟蹤誤差信號為：v₃＝z₃-ξ₃，同時選擇Lyapunov函數：對V₃求導可得：

其中，對于光滑函數f₃(Z₃)，給定ε₃≥0，有極限學習機算法H₃β₃；令f₃(Z₃)＝H₃(Z₃)β₃+δ₃(Z₃)，δ₃(Z₃)表示逼近誤差，并滿足|δ₃(Z₃)|≤ε₃，從而有：

構建真實控制率u_qs為：

定義補償誤差

按照公式(15)、(16)和(17)將公式(14)改寫為：

b.4根據微分方程對z₄求導可得誤差動態方程：定義命令濾波補償后的跟蹤誤差信號為：v₄＝z₄-ξ₄，選擇Lyapunov函數：

對V₄求導可得：

其中，f₄＝d₁x₄；對于光滑函數f₄(Z₄)，給定ε₄≥0，有極限學習機算法H₄β₄；令f₄(Z₄)＝H₄(Z₄)β₄+δ₄(Z₄)，其中，δ₄(Z₄)表示逼近誤差，并滿足|δ₄(Z₄)|≤ε₄，從而有：

構建虛擬控制信號α₄為：

定義補償誤差

按照公式(20)、(21)和(22)將公式(19)改寫為：

b.5根據微分方程對z₅求導可得誤差動態方程：定義命令濾波補償后的跟蹤誤差信號為：v₅＝z₅-ξ₅，同時選擇Lyapunov函數：對V₅求導可得：

其中，對于光滑函數f₅(Z₅)，給定ε₅≥0，有極限學習機算法H₅β₅；令f₅(Z₅)＝H₅(Z₅)β₅+δ₅(Z₅)，其中，δ₅(Z₅)表示逼近誤差，并滿足|δ₅(Z₅)|≤ε₅，從而有：

構建虛擬控制信號α₅為：

定義補償誤差

按照公式(25)、(26)和(27)將公式(24)改寫為：

b.6根據微分方程對z₆求導可得誤差動態方程：定義命令濾波補償后的跟蹤誤差信號為：v₆＝z₆-ξ₆，同時選擇Lyapunov函數：對V₆求導可得：

其中，對于光滑函數f₆(Z₆)，給定ε₆≥0，有極限學習機算法H₆β₆；令f₆(Z₆)＝H₆(Z₆)β₆+δ₆(Z₆)，其中，δ₆(Z₆)表示逼近誤差，并滿足|δ₆(Z₆)|≤ε₆，從而有：

構建真實控制律u_ds為：

定義補償誤差

按照公式(30)、(31)和(32)將公式(29)改寫為：

c對建立的基于極限學習機的電動汽車異步電機驅動系統控制方法進行穩定性分析

定義φ＝max{||β₁||²,||β₂||²,||β₃||²,||β₄||²,||β₅||²,||β₆||²}，為φ的估計值，構建Lyapunov函數為：對V求導可得：

選擇相應的自適應律

其中，r和m是正常數；按照公式(35)將公式(34)改寫為：

同時，由楊氏不等式可得：

按照公式(37)將公式(36)改寫為：

其中：

a＝min{2k₁,2(k₂-1),2(k₃-1),2(k₄-1),2(k₅-1),2(k₆-1),m}；

因而可得：

因此v_g和是有界的，因為是φ常數，所以是有界的，又因為z_g＝v_g+ξ_g，g＝1,2,...6，||ξ_g||是有界的，因此z_g也是有界的；因此x(t)和其他所有控制信號在任何時間段內都是有界的；引入命令濾波技術，通過基于極限學習機的自適應反步控制方法所設計的控制器能保證速度的跟蹤誤差能夠收斂到原點的一個充分小的鄰域內，實現對異步電機速度的高效跟蹤控制。由公式(39)可得：

本發明具有如下優點：

(1)本發明針對電動汽車在電力驅動和控制系統中存在的非線性問題，能夠使電機快速達到穩定的運行狀態，更加適合像電動汽車驅動系統這樣需要快速動態響應的控制對象；

(2)考慮鐵損的異步電機在控制律的作用下，系統的跟蹤誤差能夠收斂到原點的一個充分小的鄰域內，同時其他信號保持有界。

(3)電動汽車工作在較高轉速時，異步電機會產生較大的鐵損，本發明充分考慮到鐵損問題并構建合理模型加以合適方式有效解決此問題，與傳統的矢量控制方法相比，本發明能夠克服參數未知以及負載變化的影響，實現更加有效的速度控制。

(4)本發明需要的輸入信號是實際工程中易于得到的可直接測量的轉速和電流信號量，基于極限學習機的自適應命令濾波反步控制方法本身可以通過軟件編程實現，使用極限學習機算法來逼近電機驅動系統中未知的非線性項，同時通過引入命令濾波技術，克服了計算爆炸問題。與此同時，本發明設計的控制器具有更加簡單的結構，可以保證系統的跟蹤誤差能夠收斂到原點的一個充分小的鄰域內以及所有的閉環信號都是有界的。

(5)本發明不需要根據考慮鐵損的異步電機的不同而修改控制器的參數，原理上可以實現對所有型號和功率的異步電機的穩定調速控制，在控制過程中減少對異步電機參數的測量，利于實現考慮鐵損的異步電機轉速調節的快速響應。

(6)本發明還給出了具體的仿真結果，通過仿真結果表明本發明控制方法的有效性和魯棒性，具有較強的抗負載擾動能力，實現了理想的控制效果。

附圖說明

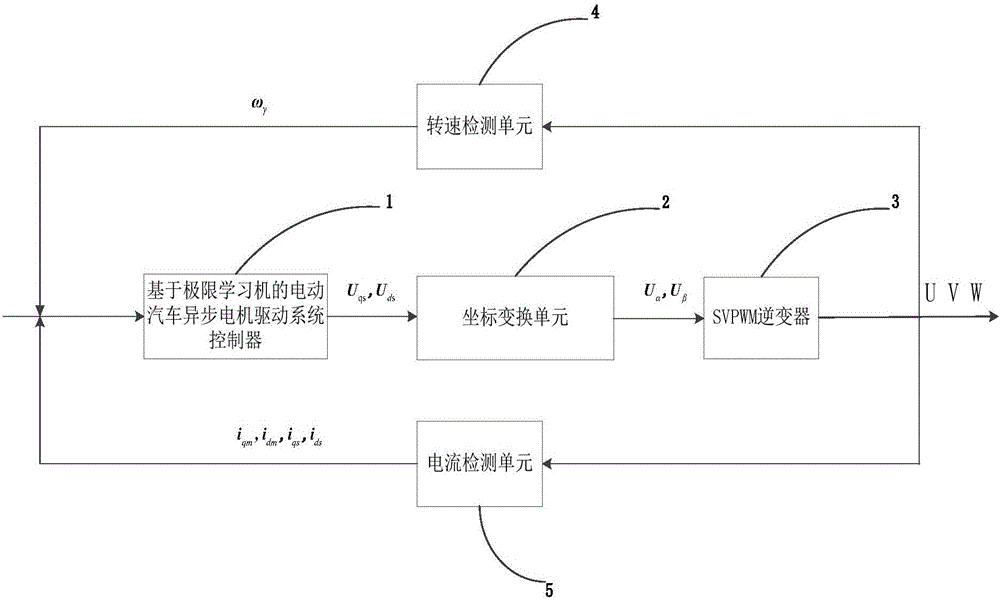
圖1為本發明中由基于極限學習機的電動汽車異步電機驅動系統控制器、坐標變換和SVPWM逆變器組成的復合被控對象的示意圖；

圖2為本發明中基于極限學習機的電動汽車異步電機驅動系統控制器控制后轉子角位置和轉子角位置設定值的跟蹤仿真圖；

圖3為本發明中基于極限學習機的電動汽車異步電機驅動系統控制器控制后轉子角位置和轉子角位置設定值的跟蹤誤差仿真圖；

圖4為本發明中基于極限學習機的電動汽車異步電機驅動系統控制器控制后轉子磁鏈和轉子磁鏈設定值的跟蹤仿真圖；

圖5為本發明中基于極限學習機的電動汽車異步電機驅動系統控制器控制后轉子磁鏈和轉子磁鏈設定值的跟蹤誤差仿真圖；

圖6為本發明中基于極限學習機的電動汽車異步電機驅動系統控制器控制后q軸定子電流仿真圖；

圖7為本發明中基于極限學習機的電動汽車異步電機驅動系統控制器控制后d軸定子電流仿真圖。

具體實施方式

本發明的基本思想為：利用極限學習機逼近考慮鐵損的異步電機系統中的高度非線性函數，并結合自適應和反步技術構造控制器，將命令濾波技術引入到遞推過程Lyapunov函數的選取和中間虛擬控制信號的構造中，遞推得到控制律，同時設計相應的自適應律來調節未知參數；引入命令濾波技術，在不進行微分運算的情況下，可以產生命令信號的導數信號，減小了計算量，解決了傳統反步法對虛擬控制函數進行連續求導引起的“計算爆炸”問題，同時通過引入誤差補償機制，極大的減小了命令濾波產生的誤差，提高了控制精度；命令濾波技術的引入極大簡化了設計過程，另外，本發明還為控制器中固定參數的選取開辟了一種新的思路，大大提高了設計效率，改善了系統穩態性能。

具體的，下面結合附圖以及具體實施方式對本發明作進一步詳細說明：

結合圖1所示，基于極限學習機的電動汽車異步電機驅動系統控制方法，其采用的部件主要包括基于極限學習機的電動汽車異步電機驅動系統控制器1、坐標變換單元2、SVPWM逆變器3和轉速檢測單元4與電流檢測單元5。其中：

轉速檢測單元4和電流檢測單元5主要用于檢測異步電機的電流值和轉速相關變量，通過實際測量的電流和轉速變量作為輸入，通過基于極限學習機的電動汽車異步電機驅動系統控制器1進行電壓控制，最終轉換為三相電控制的異步電機轉速。為了設計一個更加有效的控制器，建立考慮鐵損的異步電機動態模型是十分必要的。

基于極限學習機的電動汽車異步電機驅動系統控制方法，包括如下步驟：

a在同步旋轉坐標d-q下考慮鐵損的異步電機的動態模型如下：

其中，ω_r表示考慮鐵損的異步電機轉子角速度；J表示轉動慣量；T_L表示負載轉矩；ψ_d表示轉子磁鏈；n_p表示極對數；i_qs,i_ds表示d-q軸定子電流；u_qs,u_ds表示異步電機d-q軸定子電壓；L_m表示互感；L_1r,L_1s分別表示定轉子漏感；R_s,R_r,R_fe分別表示異步電機定、轉子及鐵損等效電阻；i_qm,i_dm分別表示d-q軸勵磁電流；i_qs,i_ds分別表示d-q軸定子電流；

為簡化考慮鐵損的異步電機的動態數學模型，定義新的變量：

則考慮鐵損的異步電機的動態數學模型表示為：

其中，

b根據命令濾波技術和自適應反步法原理，設計一種基于極限學習機的電動汽車異步電機驅動系統控制方法；

考慮鐵損的異步電機的動態數學模型簡化為兩個獨立的子系統，即由狀態變量x₁，x₂，x₃和控制輸入u_qs組成的子系統以及由狀態變量x₄，x₅,x₆和控制輸入u_ds組成的子系統；

定義命令濾波器為：

其中，均為命令濾波器的輸出信號，α_u為命令濾波器的輸入信號，u＝1,2,4,5；如果輸入信號α_u對于所有的t≥0，使得以及成立，其中，ρ₁和ρ₂均為正常數；同時則可得出，對任意的常數μ＞0，存在ω_n＞0且ζ∈(0,1]，使得和是有界的；

定義跟蹤誤差變量為：

定義x_d為期望的位置信號；虛擬控制信號α₁,α₂,α₄,α₅為命令濾波器的輸入信號；x_1,c,x_2,c,x_3,c,x_4,c,x_5,c為命令濾波器的輸出信號；k_g為正的設計參數；β_g是極限學習機算法的輸出權值向量，||β_g||是β_g的范數；H_g(Z_g)＝[G₁(a₁,b₁,Z₁),G₂(a₂,b₂,Z₂),...,G_g(a_g,b_g,Z_g)]，其中H_g(Z_g)表示極限學習機算法的隱層映射矩陣，G_g(·)是激活函數，在大多數應用中，為了簡單起見，對所有隱層節點使用的激活函數相同，(a_g,b_g)是隱層節點參數，Z_g是映射矩陣H_g(Z_g)的變量集合；l_g為正常數，g＝1,2,...,6是隱層神經元數。

控制方法的設計每一步都會選取一個合適的Lyapunov函數構建一個虛擬控制信號或者真實的控制律；控制方法的設計具體包括以下步驟：

b.1根據微分方程對z₁求導得誤差動態方程：定義命令濾波補償后的跟蹤誤差信號為：v₁＝z₁-ξ₁，同時選取Lyapunov函數：對V₁求導得：

在實際系統中負載參數T_L是有界的，定義T_L是未知的正常數且上限為d，即0≤T_L≤d；根據楊氏不等式可得：

其中，f₁＝a₁x₂x₄-x₂；對于光滑函數f₁(Z₁)，給定ε₁≥0，有極限學習機算法H₁β₁；令f₁(Z₁)＝H₁(Z₁)β₁+δ₁(Z₁)，δ₁(Z₁)表示逼近誤差，并滿足|δ₁(Z₁)|≤ε₁，從而有：

構建虛擬控制信號α₁為：

定義補償誤差

其中ξ(0)＝0，||ξ_g||是有界的，有μ＞0，ρ＞0，k_g為正的設計參數，g＝1,2,...6；

按照公式(5)、(6)和(7)將公式(4)改寫為：

b.2根據微分方程對z₂求導得誤差動態方程：定義命令濾波補償后的跟蹤誤差信號為：v₂＝z₂-ξ₂，同時選擇Lyapunov函數：

對V₂求導得：

其中，對于光滑函數f₂(Z₂)，給定ε₂≥0，有極限學習機算法H₂β₂；令f₂(Z₂)＝H₂(Z₂)β₂+δ₂(Z₂)，其中，δ₂(Z₂)表示逼近誤差，并滿足|δ₂(Z₂)|≤ε₂，從而有：

構建虛擬控制信號α₂：

定義補償誤差

按照公式(10)、(11)和(12)將公式(9)改寫為：

b.3根據微分方程對z₃求導可得誤差動態方程：定義命令濾波補償后的跟蹤誤差信號為：v₃＝z₃-ξ₃，同時選擇Lyapunov函數：對V₃求導可得：

其中，對于光滑函數f₃(Z₃)，給定ε₃≥0，有極限學習機算法H₃β₃；令f₃(Z₃)＝H₃(Z₃)β₃+δ₃(Z₃)，δ₃(Z₃)表示逼近誤差，并滿足|δ₃(Z₃)|≤ε₃，從而有：

構建真實控制率u_qs為：

定義補償誤差

按照公式(15)、(16)和(17)將公式(14)改寫為：

b.4根據微分方程對z₄求導可得誤差動態方程：定義命令濾波補償后的跟蹤誤差信號為：v₄＝z₄-ξ₄，選擇Lyapunov函數：

對V₄求導可得：

其中，f₄＝d₁x₄；對于光滑函數f₄(Z₄)，給定ε₄≥0，有極限學習機算法H₄β₄；令f₄(Z₄)＝H₄(Z₄)β₄+δ₄(Z₄)，其中，δ₄(Z₄)表示逼近誤差，并滿足|δ₄(Z₄)|≤ε₄，從而有：

構建虛擬控制信號α₄為：

定義補償誤差

按照公式(20)、(21)和(22)將公式(19)改寫為：

b.5根據微分方程對z₅求導可得誤差動態方程：定義命令濾波補償后的跟蹤誤差信號為：v₅＝z₅-ξ₅，同時選擇Lyapunov函數：

對V₅求導可得：

其中，對于光滑函數f₅(Z₅)，給定ε₅≥0，有極限學習機算法H₅β₅；令f₅(Z₅)＝H₅(Z₅)β₅+δ₅(Z₅)，其中，δ₅(Z₅)表示逼近誤差，并滿足|δ₅(Z₅)|≤ε₅，從而有：

構建虛擬控制信號α₅為：

定義補償誤差

按照公式(25)、(26)和(27)將公式(24)改寫為：

b.6根據微分方程對z₆求導可得誤差動態方程：定義命令濾波補償后的跟蹤誤差信號為：v₆＝z₆-ξ₆，同時選擇Lyapunov函數：對V₆求導可得：

其中，對于光滑函數f₆(Z₆)，給定ε₆≥0，有極限學習機算法H₆β₆；令f₆(Z₆)＝H₆(Z₆)β₆+δ₆(Z₆)，其中，δ₆(Z₆)表示逼近誤差，并滿足|δ₆(Z₆)|≤ε₆，從而有：

構建真實控制律u_ds為：

定義補償誤差

按照公式(30)、(31)和(32)將公式(29)改寫為：

c對建立的基于極限學習機的電動汽車異步電機驅動系統控制方法進行穩定性分析

定義φ＝max{||β₁||²,||β₂||²,||β₃||²,||β₄||²,||β₅||²,||β₆||²}，為φ的估計值，構建Lyapunov函數為：對V求導可得：

選擇相應的自適應律

其中，r和m是正常數。按照公式(35)將公式(34)改寫為：

同時，由楊氏不等式可得：

按照公式(37)將公式(36)改寫為：

其中：

a＝min{2k₁,2(k₂-1),2(k₃-1),2(k₄-1),2(k₅-1),2(k₆-1),m}；

因而可得：

因此v_g和是有界的，因為是φ常數，所以是有界的，又因為z_g＝v_g+ξ_g，g＝1,2,...6，||ξ_g||是有界的，因此z_g也是有界的；因此x(t)和其他所有控制信號在任何時間段內都是有界的；引入命令濾波技術，通過基于極限學習機的自適應反步控制方法所設計的控制器能保證速度的跟蹤誤差能夠收斂到原點的一個充分小的鄰域內，實現對異步電機速度的高效跟蹤控制。由公式(39)可得：

由以上分析得到在控制律u_q,u_d的作用下，系統的跟蹤誤差收斂到原點的一個充分下的鄰域內，并保證其他信號有界。

在虛擬環境下對所建立的基于極限學習機的電動汽車異步電動機驅動系統控制方法進行仿真，驗證所提出控制方法的可行性。

電機及負載參數為：

J＝0.0586Kgm²，R_s＝0.1Ω，R_r＝0.15Ω，R_fe＝30Ω,L_1s＝L_1r＝0.0699H,

L_r＝0.1379H，L_m＝0.068H,n_p＝3。

選擇控制律參數為：

k₁＝300，k₂＝400，k₃＝1200，k₄＝6400，k₅＝160，k₆＝320，

l₁＝l₂＝l₃＝l₄＝l₅＝l₆＝2.5，m＝0.8，r＝0.01,ω_n＝10000,ζ＝0.5。

選擇跟蹤信號為：

期望轉子磁鏈信號為：x_4d＝1。

負載轉矩為：

相應的仿真結果如附圖2-7所示。其中：

圖2和圖3分別為基于極限學習機的異步電動機驅動系統控制器控制后轉子角度和轉子角度設定值的跟蹤仿真圖以及轉子角度和轉子角度設定值的跟蹤誤差仿真圖；圖4和圖5分別為基于極限學習機的異步電動機驅動系統控制器控制后轉子磁鏈和轉子磁鏈設定值的跟蹤仿真圖以及轉子磁鏈和轉子磁鏈設定值的跟蹤誤差仿真圖；圖6和圖7分別為基于極限學習機的異步電動機驅動系統控制器控制異步電機q軸定子以及異步電機d軸定子電流仿真圖，通過仿真結果表明效果理想、波動小、響應速度快。

上述仿真結果表明，本發明的控制方法能夠克服參數不確定的影響并且有利于保證理想的控制效果，實現對轉速的快速、穩定地響應。

當然，以上說明僅僅為本發明的較佳實施例，本發明并不限于列舉上述實施例，應當說明的是，任何熟悉本領域的技術人員在本說明書的教導下，所做出的所有等同替代、明顯變形形式，均落在本說明書的實質范圍之內，理應受到本發明的保護。