本發明涉及無速度傳感器交流異步電機，特別涉及基于Gopinath模型的異步電機轉速估計方法。

背景技術：

異步電機現有的轉速估計方法主要包括模型參考自適應法、擴展卡爾曼濾波和高頻注入法等。

模型參考自適應法是利用兩個結構不同的電機模型來估計電機的轉子磁鏈，此方法將不含轉速因子的轉子磁鏈電壓模型作為參考模型，將含轉速因子的轉子磁鏈電流模型作為自適應模型。由兩個模型的輸出的差值來驅動自適應機制，計算出轉速估計值并將其反饋給自適應模型，以此來修正自適應模型，最終達到自適應模型的輸出跟隨參考模型的輸出。此方法的缺點是要求參考模型必須非常準確，否則自適應模型跟隨參考模型得出的結果也是不準確的。然而在異步電機低轉速階段，作為參考模型的轉子磁鏈電壓模型易受電機參數和環境的影響，因此模型參考自適應法不適用于低轉速階段。

擴展卡爾曼濾波法是對異步電機高階系統的一階近似估計，由于異步電機的控制系統是一個高階非線性時變系統，使得擴展卡爾曼濾波器很容易發散，并且只有當系統噪聲為高斯噪聲時才會得到最優估計，更重要的是，拓展卡爾曼濾波器龐大的計算支出使得其很難直接應用在異步電機的實時控制當中。

對于高頻注入法而言，它雖然脫離了傳統的濾波方法和對電機反電勢估計的基礎，利用電機結構本身的凸極性，通過對定子電流注入高頻信號，高頻信號以漏感的途徑被檢測出來，通過調制解調的辦法獲得電機的轉子位置，但由于這種方法要求電機本身具有“凸極”的特性，因此并不適用于轉子對稱結構的異步鼠籠電機。

技術實現要素：

為解決無速度傳感器異步電機在低轉速情況下，傳統的轉速估計模型易受電機參數影響、計算量大和精度不高等問題，本發明提出基于Gopinath模型的異步電機轉速估計方法。鑒于Gopinath模型會不可避免的使轉子磁鏈相位超前，因此改進Gopinath模型，通過增加相位補償環節來解決相位超前問題。

本發明的技術方案是這樣解決的：

在高轉速情況下，利用電壓模型來估計轉子磁鏈較為準確，而在低轉速情況下，利用電流模型估計轉子磁鏈較為準確，因此為了避免引入高低轉速切換模塊后造成的磁鏈估計模型結構復雜和計算量龐大等問題，特引入帶相位補償的Gopinath模型來估計轉子磁鏈，該模型將電流模型與電壓模型二者相結合，實現全階段轉速下對轉子磁鏈的精確估計，具體實現步驟如下：

首先根據Gopinath模型，將最終的轉子磁鏈ψ表示為電壓模型估算出的轉子磁鏈ψ^u與電流模型估算出的轉子磁鏈ψⁱ的組合ψ＝f(ψ^u,ψⁱ)，此外電壓模型可表示為ψ^u＝g(u_s,R_s)，電流模型可表示為ψⁱ＝h(θ,T_r)，所以最終轉子磁鏈ψ可表示為ψ＝(g(u_s,R_s),h(θ,T_r))

然后，當ψ＝(g(u_s,R_s),h(θ,T_r))中的因子u_s、R_s、θ和T_r的實際值與估算值不一致時，如和比較轉子磁鏈實際值與估算值的誤差得到影響轉子磁鏈誤差e的最主要因素是定子電壓u_s。

其次，分析可知一階高通環節是導致轉子磁鏈ψ相位超前的直接原因，它的相頻特性對Gopinath模型計算出的轉子磁鏈ψ增加值為的相位補償，得到經過相位補償后的轉子磁鏈ψ_r-comp

最終利用轉差法計算出異步電機的轉差速度，從而得出最后的轉子速度。

其中u_s代表定子電壓，R_s代表定子電阻，θ代表轉子磁鏈角，T_r代表轉子時間常數，并且在電機系統實際運行時，K_p＝10，K_I＝0.0001/0.45。

本發明帶相位補償的Gopinath模型結構簡單，計算量小，同時將高轉速情況下的電壓模型和低轉速情況下的電流模型有效的結合在一起，實現了在無切換模塊的情況下對全階段轉速下的轉子磁鏈進行準確的估計，進而估算出轉子速度。經驗證，此模型在低轉速情況下可以準確的估算出異步電機轉速。

附圖說明

圖1一階高通濾波器的伯德圖

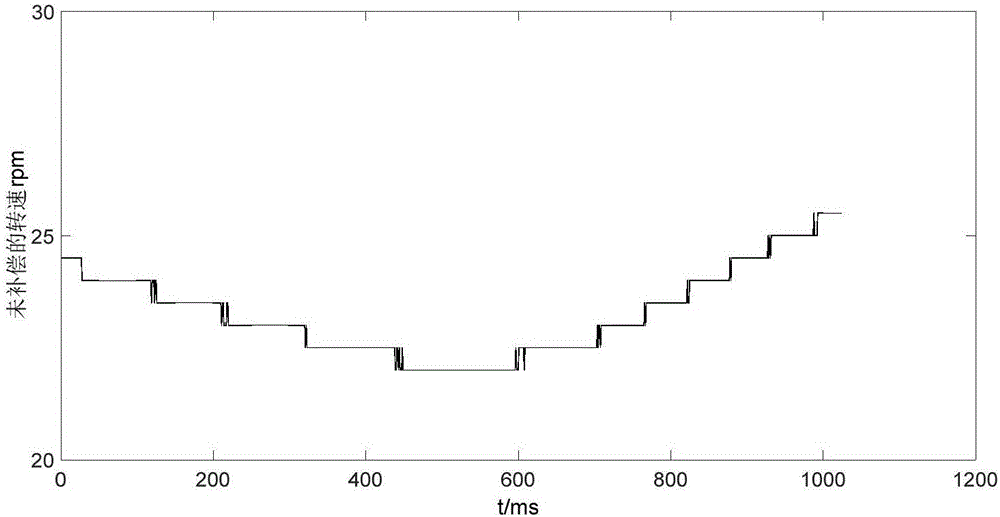
圖2無相位補償的Gopinath模型下的轉速圖

圖3一階低通濾波器的伯德圖

圖4有相位補償的Gopinath模型下的轉速圖

具體實施方式

1.Gopinath模型

Gopinath模型下的轉子磁鏈ψ如下所示：

經推導，可以得出：

其中：

ψ代表Gopinath模型估算出的磁鏈，ψ^u代表電壓模型估算出的磁鏈，ψⁱ代表電流模型估算出的磁鏈，是一階高通濾波器環節。

由式2可知，轉子磁鏈ψ由電壓模型下的轉子磁鏈ψ^u和電流模型下的轉子磁鏈ψⁱ共同決定，因此這兩個模型的估算誤差都會影響到最終的轉子磁鏈誤差，下面依次分析這兩個模型對磁鏈估計的影響。

(1)電流模型

電流模型下轉子磁鏈是由勵磁電流分量I_d計算而來，而I_d是由定子電流I_s經Park變換得到的，流程如下：

因此共有Park變換模塊和轉子時間常數T_r兩個因素可以影響到轉子磁鏈的精度，下面依次分析

①PARK變換模塊

Park變換轉矩如公式3所示：

若轉子位置角存在Δθ的誤差，則Park矩陣可表示為：

經推導，Park矩陣可表示為：

由于轉子位置角估計誤差Δθ→0所以cosΔθ≈1，sinΔθ≈0

因此由此可以證明轉子位置角的偏差對磁鏈估計不會有太大影響。

②轉子時間常數

轉子時間常數T_r的增大或者減小會影響這個一階慣性環節的截止頻率，但這只是一種動態的影響，當系統處于穩態時，T_r并不會影響穩態結果。

綜合可得：電流模型的誤差對轉子磁鏈的影響可以忽略不計

(2)電壓模型

電壓模型下轉子磁鏈估計如下：

ψ^u＝∫(u_s-i_sR_s)dt (6)

因此電壓模型的誤差來源只有u_s和R_s兩方面。

①定子電阻R_s

在單位標幺制下，假設定子電阻估計值那么

其中為定子電阻估計誤差引入的誤差項。當電機運行在低速重載的情況下時，取u_s≈0.1pu，i_s≈0.5pu，可以得出誤差項的實際值可以看出即使在電流很大的情況下，ΔR_s變化50％，定子電阻的誤差造成的影響也不會超過10％，因此定子電阻R_s對轉子磁鏈估計并無太大影響。

②定子電壓u_s

由于矢量控制中是通過占空比的大小來估計線電壓，因此估計出的u_s應該是一個理想方波，而實際的u_s在上升、下降沿期間表現為階梯波，這就導致估計出的大于實際的由電壓模型下的磁鏈估計公式ψ^u＝∫(u_s-i_sR_s)dt可知，對u_s的估計偏大會導致對ψ^u估計偏大。一階高通環節的伯德圖如圖1所示，由圖1可以看出在低頻處，相位超前較大，即當ω→0時，因此，對u_s的估計偏大將導致最終轉子磁鏈的估計值產生較大的相位超前。

綜合可得：電壓模型下u_s的誤差是影響轉子磁鏈估計的最主要因素。

2.引入相位補償

利用轉差法可以估算異步電機的轉差速度，如下所示：

在理想的FOC中，當轉速為正時，定子電流I_s的相位應該超前ψ_r，因此轉差法計算出的轉差速度ω_slip應該大于0。由上述可知，在低轉速情況下，對u_s的估計偏大將導致ψ_r相位超前，甚至超前于I_s，使得轉差法計算出的轉差速度小于0，這顯然不符合常理，這種錯誤輕則不能準確估計轉子轉速，重則影響整個電機執行器的系統穩定性。無相位補償的Gopinath模型下的轉速估計圖如圖2所示，其中電機給定的實際轉速為30rpm，最終估算出的轉速為25rpm左右，由此可見，估計轉速與實際轉速之間誤差較大。

為了解決該問題，改進Gopinath模型，通過對ψ_r引入相位補償環節以提升轉速估計的精度。

由Gopinath模型可以看出，是一個低通濾波器，伯德圖如圖3所示，在低頻段區間，當ω→0時，因此電流模型在低頻段對ψ的幅頻和相頻影響可以忽略不計，為了簡化計算，可以忽略電流模型誤差帶來的影響，只針對電壓模型進行相位補償。

一階高通環節F(s)的相頻特性可表示如下：

因此取對轉子磁鏈進行相位補償后，再估算轉差速度ω_s，具體改進流程如下：

首先通過Gopinath模型估算轉子磁鏈ψ_r，然后將轉子磁鏈ψ_r經過進行相位補償得到補償后的轉子磁鏈ψ_r-comp，將補償后的轉子磁鏈與定子電流i_s相乘得到轉差速度ω_slip，最后經過一個低通濾波器即可計算出最終的轉差速度。引入相位補償環節的Gopinath模型轉速估計圖如圖4所示，其中電機給定的實際轉速為30rpm，最終估算出的轉速為30rpm左右，經驗證，帶相位補償的Gopinath模型可以準確估算出轉子轉速。