本發明涉及一種基于全狀態反饋的逆變器有源阻尼控制方法，屬于分布式并網發電技術領域。

背景技術：

基于lcl型濾波器的并網逆變器相比于單電感并網逆變器，具有顯著的優勢，但是存在諧振問題。特別在分布式微網中，電網阻抗較大且隨運行方式而改變，由此引起lcl濾波器的帶寬變化和相位偏移，影響其控制性能，甚至可能導致系統不穩定。

在同步坐標系下，三相交流信號經過abc/dq坐標變換為兩相直流信號。但是變換得到的dq分量間存在耦合，該問題在lcl濾波器情況下變得尤為突出，嚴重影響控制系統的動態性能。此外，上述方法需要對電壓和電流分別進行派克變換以及一次電壓反派克變換，增加了算法的復雜程度。

基于lcl型濾波器的諧振抑制方法以無源阻尼控制和有源阻尼控制兩類為主。然而，無源阻尼控制通過在lcl濾波器的濾波電容串聯電阻阻尼或增加諧波回路，從而消除lcl的固有諧振頻率點，具有結構簡單的特點，但是阻尼功耗大，逆變器效率低，并且存在高頻諧波衰減能力差的不足。有源阻尼控制技術主要通過在電流閉環控制中設計諧振抑制控制算法，來抑制lcl濾波器固有的諧振峰。

技術實現要素：

本發明目的在于提出一種基于全狀態反饋的逆變器有源阻尼控制方法，它是一種不需要在濾波支路增加電阻等無源裝置的lcl型并網逆變器有源阻尼控制方法，以解決lcl型并網逆變器固有的諧振問題，有效改善了逆變器的效率和穩定性。

本發明提出的一種基于全狀態反饋的逆變器有源阻尼控制方法，是一種在靜止坐標系下的有源阻尼控制方法，具有算法簡單、可靠性高的優點。采用基于全狀態反饋的逆變器有源阻尼控制方法，可以對lcl型并網逆變器三個極點的位置任意匹配，并且設計過程簡單實用。

實現上述目的，本發明采取的技術方案如下：

步驟一：在每個采樣周期內對橋臂電流i1、逆變器并網電流i2和濾波電容電壓uc進行不對稱規則采樣；

步驟二：并網電流給定值和反饋值i2相減，得到的電流誤差值經過比例-諧振調節器，輸出并網電流調節器的控制信號uctrl；

步驟三：將狀態量橋臂電流i1、濾波電容電壓uc和并網電流i2分別和狀態反饋系數k1，k2，k3相乘，得到全狀態反饋信號ufeed；

步驟四：將并網電流調節器的輸出控制信號uctrl和全狀態反饋信號ufeed相減，再加上公共耦合點電壓的前饋信號upcc，作為逆變器的調制信號

步驟五：將逆變器調制信號與高頻三角載波進行比較，產生pwm脈沖。

本發明相對于現有技術的有益效果是：

本發明是在逆變器電流環的基礎上做出的改進，設計出了一種基于兩相靜止坐標系下準pr電流調節和lcl濾波器全狀態反饋的有源阻尼控制方法，通過在電流閉環調節信號上疊加系統狀態反饋的補償量，抑制lcl型并網逆變器的諧振。首先該方法是一種有源阻尼控制，無需加入阻尼電阻，有效提高了逆變器的工作效率、穩定性和高頻諧波的衰減能力。其次，基于全狀態反饋的逆變器有源阻尼控制方法不存在坐標系解耦帶來的算法復雜和可靠性低的問題，逆變器的控制裝置結構相對簡單，易于實現。

附圖說明

圖1為本發明的一種基于全狀態反饋的逆變器有源阻尼控制方法的lcl型并網逆變器主電路及其控制裝置結構圖；

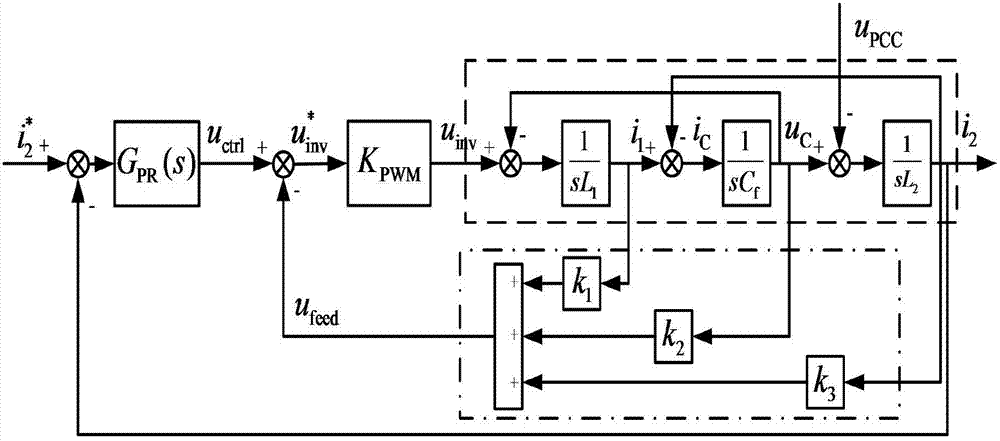
圖2為本發明的一種基于全狀態反饋的逆變器有源阻尼控制方法的控制框圖；

圖3為本發明的實施例1的lcl型并網逆變器無阻尼與有源阻尼的極點分布圖；

圖4為本發明的實施例1的lcl型并網逆變器無阻尼與有源阻尼的bode圖；

圖5為本發明的實施例1加入準pr調節的逆變器電流開環頻率響應特性圖；

圖6為本發明的實施例1投入有源阻尼的仿真波形圖。

下面結合附圖對本發明的技術方案作進一步的說明，但并不局限于此，凡是對本發明技術方案進行修改或者等同替換，而不脫離本發明技術方案的精神和范圍，均應涵蓋在本發明的保護范圍中。

具體實施方式

具體實施方式一：如圖1所示，一種基于全狀態反饋的逆變器有源阻尼控制方法：

步驟一：在每個采樣周期內對橋臂電流i1、逆變器并網電流i2和濾波電容電壓uc進行不對稱規則采樣；

步驟二：并網電流給定值和反饋值i2相減，得到的電流誤差值經過比例-諧振調節器，輸出并網電流調節器的控制信號uctrl；

步驟三：將狀態量橋臂電流i1、濾波電容電壓uc和并網電流i2分別和狀態反饋系數k1，k2，k3相乘，得到全狀態反饋信號ufeed；

步驟四：將并網電流調節器的輸出控制信號uctrl和全狀態反饋信號ufeed相減，再加上公共耦合點電壓的前饋信號upcc，作為逆變器的調制信號

步驟五：將逆變器調制信號與高頻三角載波進行比較，產生pwm脈沖。

具體實施方式二：本實施方式是對具體實施方式一作出的進一步說明，所述的步驟三中，狀態反饋系數k1，k2，k3的取值為：

對于lcl濾波器的狀態空間模型∑0

式中x——狀態變量矩陣；

y——輸出變量矩陣；

u——輸入變量矩陣；

——狀態變量導數矩陣；

a——狀態矩陣；

b——輸入矩陣；

c——輸出矩陣。

通過狀態反饋矩陣k，有

det[λi-(a-bk)]＝f^*(λ)

式中det——計算矩陣行列式；

λ——系統矩陣的特征值；

k——狀態反饋矩陣；

i——單位矩陣；

a——狀態矩陣；

b——輸入矩陣；

f^*(λ)——系統期望矩陣的特征多項式；

式中f^*(λ)——系統期望矩陣的特征多項式；

λ——系統矩陣的特征值；

——系統期望矩陣的第i個特征值；

——系統期望矩陣的特征多項式二次項的系數；

——系統期望矩陣的特征多項式一次項的系數；

——系統期望矩陣的特征多項式常數項的系數；

π——累乘運算符；

存在非奇異變換將∑0變換為能控標準型

式中——非奇異變換下的狀態變量導數矩陣。

——非奇異變換下的狀態變量矩陣；

p——非奇異變換矩陣；

a——狀態矩陣；

b——輸入矩陣；

u——輸入變量矩陣；

y——輸出變量矩陣；

c——輸出矩陣；

p^-1——非奇異變換矩陣的轉置；

——非奇異變換下的狀態矩陣；

——非奇異變換下的輸入矩陣；

——非奇異變換下的輸出矩陣；

對應的閉環特征多項式為：

式中——非奇異變換矩陣p作用下的反饋系數；

a1，a2，a3——系統矩陣特征多項式的系數；

f(λ)——系統期望的特征多項式；

det——計算矩陣行列式；

λ——系統矩陣的特征值；

i——單位矩陣；

——非奇異變換下的狀態反饋矩陣；

——非奇異變換下的狀態矩陣；

——非奇異變換下的輸入矩陣；

因此，非奇異變換下的狀態反饋矩陣

式中——非奇異變換下的狀態反饋矩陣；

——系統期望矩陣的特征多項式二次項的系數；

——系統期望矩陣的特征多項式一次項的系數；

——系統期望矩陣的特征多項式常數項的系數；

a1，a2，a3——系統矩陣特征多項式的系數；

由此，得到lcl濾波器模型∑0的狀態反饋矩陣k

式中k——狀態反饋矩陣；

——非奇異變換下的狀態反饋矩陣；

p——非奇異變換矩陣。

實施例1：

本實施例披露了一種全狀態反饋的逆變器有源阻尼控制方法，屬于逆變器并網電流閉環控制的一種改進控制方法。該控制方法不需要調整lcl濾波器和并網逆變器電流環的控制參數，只需增加狀態反饋通道有源阻尼環節的控制參數。

本發明的基于全狀態反饋的逆變器有源阻尼控制方法如下：

如圖1所示，lcl型并網逆變器包括主電路和控制裝置兩部分，其中，虛線以下部分為本發明應用于lcl型并網逆變器的全狀態反饋有源阻尼控制和電流閉環控制裝置。

圖2是本發明的一種基于全狀態反饋的逆變器有源阻尼控制方法的控制框圖。

對應于圖1中電流環給定值和并網電流i2，通過pr調節器模塊gpr(s)輸出為uctrl(uctrl為并網電流調節器的控制信號)。在αβ靜止坐標系下的分量，在加入狀態反饋補償信號ufeed后，與高頻的三角載波進行比較，生產pwm開關序列。逆變器的控制裝置可以控制igbt(絕緣柵雙極型晶體管)的開通關斷，其傳遞函數為比例放大系數kpwm＝udc/2，其中udc為直流母線電壓。

其中虛線框內為lcl濾波器的等效數學模型，傳遞函數可表示為：

式中l1——逆變側電感；

l2——網側電感；

cf——濾波支路電容；

i2——并網電流；

uinv——橋臂電壓；

s——拉普拉斯算子。

采用狀態反饋的有源阻尼方法如圖2中點劃線框所示，將狀態量i1，uc，i2反饋到逆變器控制信號的輸入位置。通過對中間狀態量i1和uc的利用，計算出全狀態反饋信號ufeed，提前調整逆變器的輸出電壓uinv，增強濾波器的穩定性。

圖3是lcl型并網逆變器無阻尼與有源阻尼的極點分布圖。

極點分布圖虛軸上的三個極點為lcl型并網逆變器無阻尼的情況，系統處于臨界穩定的狀態。由于一對無阻尼共軛極點的存在，lcl型并網逆變器將發生諧振現象。

lcl型并網逆變器的無阻尼固有諧振頻率ωn

式中ωn——無阻尼固有諧振頻率；

l1——逆變側電感；

l2——網側電感；

cf——濾波支路電容。

lcl型并網逆變器極點的分布情況決定了系統的穩定性和暫態響應性能，本發明利用狀態反饋控制重新配置逆變器的極點，引入有源阻尼抑制lcl型并網逆變器的諧振峰，同時在系統中低頻段進行相位補償，使得經過極點配置改造后的系統具備一定的穩定性，并在指令跟蹤時具有理想的暫態響應速度。

基于全狀態反饋有源阻尼控制方法的lcl型并網逆變器的開環傳遞函數可表示為：

式中s1、s2、s3——lcl型并網逆變器期望的極點；

p1、p2、p3——s域內lcl型并網逆變器期望的極點位置；

l1——逆變側電感；

l2——網側電感；

cf——濾波支路電容；

i2——并網電流；

uinv——橋臂電壓。

其中s1和s2為主導極點，s3為一個遠極點，并且系統的性能主要由主導極點決定的，遠極點只有微小的影響。根據系統的設計要求：輸出超調mp≤5％，峰值時間tp≤0.5ms。經過計算可以得出阻尼比ξ≥0.707，主導極點的無阻尼固有諧振頻率ωn≥10472rad/s。

為了在諧振頻率ωr處發揮有源阻尼的作用，主導極點的無阻尼固有諧振頻率ωn不得低于諧振頻率ωr。同時ωn的值應在ωr附近，以免輕載時狀態反饋控制的作用被削弱。

確定了主導極點

式中s1,2——lcl型并網逆變器期望的一對主導極點；

j——虛部單位；

ξ——阻尼比；

ωn——無阻尼固有諧振頻率；

選取遠極點s3使它和原點的距離大于5|s1|，則有lcl濾波器狀態空間模型∑0期望的特征多項式

式中f^*(λ)——系統期望矩陣的特征多項式；

λ——系統矩陣的特征值；

——系統期望矩陣的第i個特征值；

——系統期望矩陣的特征多項式二次項的系數；

——系統期望矩陣的特征多項式一次項的系數；

——系統期望矩陣的特征多項式常數項的系數；

π——累乘運算符。

存在非奇異變換將∑0變換為能控標準型

式中——非奇異變換下的狀態變量導數矩陣。

——非奇異變換下的狀態變量矩陣；

p——非奇異變換矩陣；

a——狀態矩陣；

b——輸入矩陣；

u——輸入變量矩陣；

y——輸出變量矩陣；

c——輸出矩陣；

p^-1——非奇異變換矩陣的轉置；

——非奇異變換下的狀態矩陣；

——非奇異變換下的輸入矩陣；

——非奇異變換下的輸出矩陣。

對應的閉環特征多項式為

式中——非奇異變換矩陣p作用下的反饋系數；

a1，a2，a3——系統矩陣特征多項式的系數；

f(λ)——系統期望的特征多項式；

det——計算矩陣行列式；

λ——系統矩陣的特征值；

i——單位矩陣；

——非奇異變換下的狀態反饋矩陣；

——非奇異變換下的狀態矩陣；

——非奇異變換下的輸入矩陣。

因此，非奇異變換下的狀態反饋矩陣

式中——非奇異變換下的狀態反饋矩陣；

——系統期望矩陣的特征多項式的系數；

a1，a2，a3——系統矩陣特征多項式的系數。

由此，得到lcl濾波器模型∑0的狀態反饋矩陣k

式中k——狀態反饋矩陣；

——非奇異變換下的狀態反饋矩陣；

p——非奇異變換矩陣。

即k＝[k1k2k3]為lcl濾波器狀態空間模型∑0的狀態反饋系數矩陣。

基于狀態反饋控制的濾波器開環傳遞函數極點分布如圖3中方形點所示，有源阻尼的濾波器擁有了期望的阻尼和理想的動靜態性能。

圖4是lcl型并網逆變器無阻尼與有源阻尼的bode圖。

圖4比較了狀態反饋的有源阻尼對濾波器動態響應的改善作用。可以看出無阻尼lcl濾波器在中頻段具有較大的幅值和相位失真，在諧振頻率fr處存在諧振尖峰，同時相位發生-180^°跳變，導致并網逆變器不穩定。加入有源阻尼后的濾波器在中低頻段增益為一個定值，在高頻段增益迅速衰減，對高次諧波具有較好的抑制效果。

圖5是加入準pr調節的逆變器電流開環頻率響應特性圖。

基于αβ坐標系的lcl濾波器數學模型中的物理量為交流值，因此其電流環不能使用pi調節器。本發明使用αβ靜止坐標系的pr調節器，具有與dq旋轉坐標系下的pi調節器等價的控制效果。

pr調節器在基波頻率ω0處擁有無窮大的增益，可實現與ω0頻率指令的零穩態誤差跟蹤。圖5中采用pr調節器的電流開環增益在ω0處存在諧振峰，對閉環內部擾動具有極強的抑制能力，從而實現并網電流i2對指令電流基波分量的無靜差跟蹤。

然而，實際系統無法實現ω0頻率處增益無窮大，并且當電網頻率偏移時，pr調節器在非基頻處的增益非常小，不能有效地抑制電網引起的諧波。因此，本發明采用增益和帶寬可調的準pr調節器，相當于增大了基頻段的等效輸出阻抗，提高了系統對基頻信號的抗擾能力，其控制規律為：

式中gpr(s)——準pr調節器傳遞函數；

kp——比例控制系數，取值與系統的響應速度成正比；

kr——諧振控制系數，取值與基波頻率處的靜態誤差成反比；

ω0——基波頻率，取314rad/s；

ωc——調節器的諧振帶寬，取值與諧振頻率偏移敏感度成反比；

s——拉普拉斯算子。

本發明在電流環的前向通道加入準pr調節器，根據相角裕度γ>45°，幅值裕度kg>20db的要求，設計準pr調節器。

圖6為本發明實施例1投入有源阻尼的仿真波形圖。

投入有源阻尼前，逆變器的并網電流發生嚴重振蕩現象，甚至導致系統不穩定。而在0.005s投入有源阻尼時，逆變器的并網電流快速恢復穩定。

實施例2

本實施例披露了一種基于全狀態反饋的逆變器有源阻尼控制方法，包括如下步驟：

步驟一：在每個采樣周期內對橋臂電流i1、逆變器并網電流i2和濾波電容電壓uc進行不對稱規則采樣，并通過控制裝置中的零階保持器使采樣值在一個采樣周期內保持不變。

步驟二：abc-αβ坐標變換模塊，將橋臂電流i1、逆變器并網電流i2和濾波電容電壓uc進行clark變換，得到αβ坐標系下解耦的采樣值，從而避免了dq變換和復雜的解耦過程。有uctrl為pr調節器輸出的控制信號，表示逆變器的調制信號，uinv為逆變器的橋臂電壓。

步驟三：取逆變側電感電流、濾波電容電壓和網側電感電流x＝[i1uci2]^t為狀態變量，逆變器的橋臂電壓uinv為輸入量，并網電流i2為輸出量，建立lcl濾波器的狀態空間模型∑0

式中x——狀態變量矩陣；

y——輸出變量矩陣；

u——輸入變量矩陣；

——狀態變量導數矩陣；

a——狀態矩陣；

b——輸入矩陣；

c——輸出矩陣。

其中，

c＝[001]

式中l1——逆變側電感；

l2——網側電感；

cf——濾波支路電容；

步驟四：基于αβ坐標系的lcl濾波器數學模型中個物理量為交流值，因此其電流環不能使用pi調節器。αβ靜止坐標系的pr調節器與dq旋轉坐標系下的pi調節器具有等價的控制效果。

pr調節器在基波頻率ω0處擁有無窮大的增益，可實現與ω0頻率指令的零穩態誤差跟蹤。