本發(fā)明涉及一種基于nlms自適應(yīng)濾波的信號處理方法，屬于信號處理領(lǐng)域。

背景技術(shù)：

信息是一個比較抽象的概念，它包含在消息中，是通信系統(tǒng)中傳送的對象。消息是具體的但不是物理的，例如語言、文字、符號等。信號是信息的載體，是表示消息的物理量，例如幅度、頻率和相位都可代表消息。在接收信號時，符號間干擾和噪聲(內(nèi)部熱噪聲和外部干擾)都使信號受到損傷。信號處理的核心問題是信號的表示、變換和運算，并且提取其中的特征和信息。

自適應(yīng)信號處理是信號處理領(lǐng)域的一個非常重要的分支。作為自適應(yīng)信號處理基礎(chǔ)的自適應(yīng)濾波理論已經(jīng)成為信號處理學(xué)科的重要組成部分。四十多年來,自適應(yīng)濾波理論一直受到普遍的重視,并得到了不斷的發(fā)展和完善。尤其是近年來,隨著超大規(guī)模集成電路技術(shù)和計算機技術(shù)的迅速發(fā)展,出現(xiàn)了許多性能優(yōu)異的高速信號處理專用芯片和高性能的通用計算機,特別是為自適應(yīng)濾波器的發(fā)展和應(yīng)用提供了重要的物質(zhì)基礎(chǔ)。另一方面,信號處理理論和應(yīng)用的發(fā)展,也成為自適應(yīng)濾波理論的進一步發(fā)展提供了必要的理論基礎(chǔ)。可以這樣說,自適應(yīng)濾波理論和信號處理技術(shù)正在日益受到人們的重視,已經(jīng)并將繼續(xù)在諸如通信、雷達(dá)、聲吶、自動控制、圖像和語音處理、模式識別、生物醫(yī)學(xué)、以及地震勘探等領(lǐng)域得到廣泛的應(yīng)用,并推動這些領(lǐng)域的進步。

在實際測量中，由于未知因素的影響導(dǎo)致測量結(jié)果產(chǎn)生誤差，有時甚至與實際數(shù)據(jù)相差太大，因而怎樣通過測量數(shù)據(jù)獲得比較精確的實際數(shù)據(jù)是一個十分重要的數(shù)據(jù)處理問題。

技術(shù)實現(xiàn)要素：

為了解決上述問題，本發(fā)明通過提供一種基于nlms自適應(yīng)濾波的信號處理方法。

本發(fā)明采用的技術(shù)方案一方面為一種基于nlms自適應(yīng)濾波的信號處理方法，其特征在于，包括以下步驟：通過fir濾波器對待處理信號進行預(yù)處理，輸出濾波器信號；對濾波器信號進行歸一化最小均方誤差自適應(yīng)濾波和歸一化最小均方誤差自適應(yīng)預(yù)測處理。

優(yōu)選地，所述fir濾波器為基于kasier窗設(shè)計，其時域w[n]表達(dá)式為：

式中io(β)為零階的第一類修正貝塞爾函數(shù)。

優(yōu)選地，所述第一類修正貝塞爾函數(shù)基于以下公式：

優(yōu)選地，對濾波器信號進行歸一化最小均方誤差自適應(yīng)濾波步驟包括：

比較原信號和濾波器信號獲取誤差序列，獲取其均值：

獲取其均方值：

采用變換步長的方式縮短自適應(yīng)收斂過程，步長公式為：w(n+1)＝w(n)+e(n)x(n)，式中，e(n)x(n)為濾波權(quán)矢量迭代更新的調(diào)整量；使用平方誤差代替均方誤差以修改權(quán)矢量，獲得修正的權(quán)系數(shù)迭代公式：w(n+1)＝w(n)+uγ+xt(n)x(n)e(n)x(n)，則步長u(n)＝w(n+1)-w(n)，即u(n)＝uγ+xt(n)x(n)e(n)x(n)，其中，0≤γ≤1，0<u<2，e(n)x(n)＝1，基于γ的變化，使步長由大逐漸變小，加速收斂過程。

優(yōu)選地，所述歸一化最小均方誤差自適應(yīng)預(yù)測處理基于自適應(yīng)算法。

本發(fā)明的有益效果為通過對待處理信號先進行fir濾波器處理，然后基于歸一化最小均方誤差即nlem再次進行處理，通過多次處理以提高信號處理效率和處理效果。

附圖說明

圖1所示為基于本發(fā)明實施例的一種基于nlms自適應(yīng)濾波的信號處理方法的示意圖；

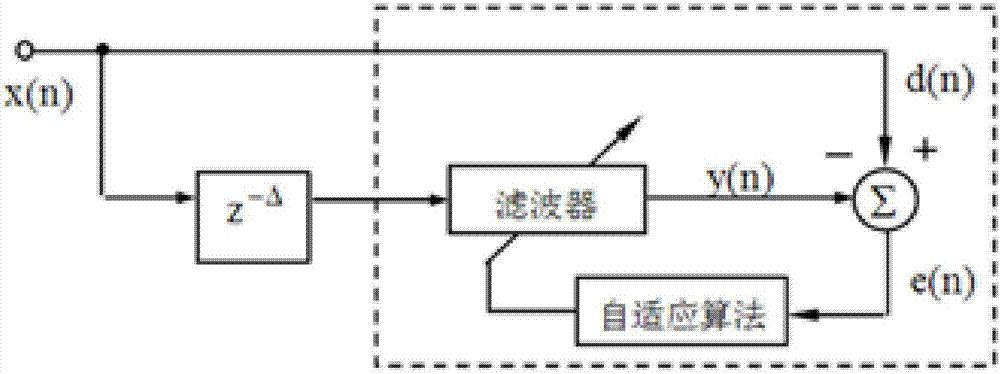
圖2所示為基于本發(fā)明實施例的自適應(yīng)預(yù)測濾波器結(jié)構(gòu)框架圖。

具體實施方式

以下結(jié)合實施例對本發(fā)明進行說明。

基于發(fā)明的實施例，如圖1所示一種基于nlms自適應(yīng)濾波的信號處理方法，其特征在于，包括以下步驟：通過fir濾波器對待處理信號進行預(yù)處理，輸出濾波器信號；對濾波器信號進行歸一化最小均方誤差自適應(yīng)濾波和歸一化最小均方誤差自適應(yīng)預(yù)測處理。

濾波器的單位脈沖響應(yīng)是一個有限長序列設(shè)單位脈沖響應(yīng)h(n)長度為n其系統(tǒng)函數(shù)h(z)和差分函數(shù)分別為：

所述fir濾波器為基于kasier窗設(shè)計，其時域w[n]表達(dá)式為：

式中io(β)為零階的第一類修正貝塞爾函數(shù)。

kaiser窗設(shè)計的濾波器具有嚴(yán)格的線性相位特性，它由零階貝塞爾函數(shù)構(gòu)成，其主瓣能量與旁瓣能量之比近乎最大，且可自由選擇主瓣寬度和旁瓣高度間的比重。

所述第一類修正貝塞爾函數(shù)基于以下公式：

在經(jīng)過上述kaiser窗設(shè)計的濾波器得到測量數(shù)據(jù)的修正值后，進過nlms自適應(yīng)濾波進行進一步修正，nlms算法是采用變步長的方法來縮短自適應(yīng)收斂過程。

對濾波器信號進行歸一化最小均方誤差自適應(yīng)濾波步驟包括：

比較原信號和濾波器信號獲取誤差序列，獲取其均值

獲取其均方值：

采用變換步長的方式縮短自適應(yīng)收斂過程，步長公式為：w(n+1)＝w(n)+e(n)x(n)，式中，e(n)x(n)為濾波權(quán)矢量迭代更新的調(diào)整量；

式中，e(n)x(n)表示濾波權(quán)矢量迭代更新的調(diào)整量。為了達(dá)到快速收斂的目的，必須合適的選擇變步長的值，一個可能策略是盡可能多地減少瞬時平方誤差，即用瞬時的平方誤差作為均方誤差的mse，這也是lms算法的基本思想。

使用平方誤差代替均方誤差以修改權(quán)矢量，獲得修正的權(quán)系數(shù)迭代公式：w(n+1)＝w(n)+uγ+xt(n)x(n)e(n)x(n)，則步長u(n)＝w(n+1)-w(n)，即u(n)＝uγ+xt(n)x(n)e(n)x(n)，其中，0≤γ≤1，0<u<2，e(n)x(n)＝1，基于γ的變化，使步長由大逐漸變小，加速收斂過程。

參數(shù)γ是為了避免xt(n)x(n)過小導(dǎo)致步長太大而設(shè)置的，0≤γ≤1。為了保證自適應(yīng)濾波器能夠穩(wěn)定工作，固定收斂因子u的選取應(yīng)滿足的數(shù)值范圍如下：0<u<2。

所述歸一化最小均方誤差自適應(yīng)預(yù)測處理基于自適應(yīng)算法。

而在僅知測量數(shù)據(jù)當(dāng)前及以前的數(shù)據(jù)情況下，為進一步修正實際數(shù)據(jù)和測量數(shù)據(jù)之間的誤差，可采用自適應(yīng)預(yù)測濾波器實現(xiàn)，一種僅由測量數(shù)據(jù)，得出實際數(shù)據(jù)的自適應(yīng)預(yù)測濾波器結(jié)構(gòu)框架圖如圖2所示，其中，

濾波器的輸入序列為理想序列：x(n)＝[x(n-△)x(n-△-1)…x(n-△-l)]^t，

權(quán)值為w(n)＝[w0(n)w1(n)…wl(n)]^t，

則濾波器輸出就為：y(n)＝x^t(n)w(n)，

預(yù)測誤差為：e(n)＝d(n)-y(n)，

延遲單元z^-△。

基于預(yù)測的誤差的自適應(yīng)反饋，提高信號處理能力。

以上所述，只是本發(fā)明的較佳實施例而已，本發(fā)明并不局限于上述實施方式，只要其以相同的手段達(dá)到本發(fā)明的技術(shù)效果，都應(yīng)屬于本發(fā)明的保護范圍。在本發(fā)明的保護范圍內(nèi)其技術(shù)方案和/或?qū)嵤┓绞娇梢杂懈鞣N不同的修改和變化。