本發明屬于計算機無線通信技術領域，涉及在基站集成無線網絡環境下,一種基于新貪心策略的按需服務數據包調度貪心算法。

背景技術：

本文應用一種基于信息站的三層網絡架構，即內容服務器，信息站(路邊通信單元)和車載設備(用戶)，系統中的網絡數據服務方式為按需服務方式。這種網絡架構和服務方式現在已經廣泛應用于服務高速列車乘客的網絡需求和V2X車聯網系統通信中。在該系統中，基站通過穩定的網絡連接與內容服務器相連，當車載設備(用戶)按照需求請求數據服務時，數據報文將通過基站與車載設備或終端(手機，電腦等)之間的無線信道調度和分配給用戶。

為了滿足車輛在告訴行駛過程中基站與車輛通信的需求，克服開普勒效應等對網絡通信的影響，有學者提出一種專門用于基站與車載設備通信的MAC幀結構。這種結構下，每個時間區間被分為時間間隔相等的用于信息傳播的時隙，時間間隔小于信道相干時間(channel coherence time)，劃分的每個時隙的信道增益是固定的，但是由于信號衰減等原因，時隙的容量會因不同的情況而有所差異。考慮時隙中信道增益等信道信息，應用自適應調制和編碼技術，每個時隙可以發送的數據包數量上限可以得出。

考慮網絡通信的質量，為了滿足用戶良好的網絡體驗，高質量、低延遲、低丟包率等要求是基站調度數據包時要追求的目標。Mohit Agarwal和Anuj Puri在2002年的論文中提出了一種服務請求模型。在按需請求數據服務下，用戶愿意為不同的服務付出的代價也是不同，另外由于用戶之間的差異，不同用戶愿意為請求服務支付的價格也不盡相同，怎樣合理高效利用信道，在上述幀結構下合理調度服務數據，使得調度的服務數據獲得最大價值，使得服務運營商或提供者獲得最大收益也是一種很重要的目標。基于該目標，該調度問題將被轉化為一個搶占式單機調度問題，本發明的目標就是如此。

現在已經有學者將上述問題轉化為目標函數為一個整數最優規劃的問題，能夠證明求解該整數最優規劃問題是一個NP困難的問題，不能在線性時間內找到最優解。

很多學者提出了很多解決上述問題的算法,例如EDF算法，FIFO算法，還有基于其他效用函數(例如指數容量等)的貪心算法，但是目前算法得到的效果普遍不高，還有可以優化的余地。

技術實現要素：

為解決現有技術中存在的問題，本發明提出一種基于新貪心策略的按需服務數據包調度貪心算法，將按需服務的數據包調度問題轉化為整數最優規劃問題，進而轉化為0-1最優規劃問題，利用貪心算法依照提出的效用函數值作為貪心策略對該問題進行優化求解。

本發明所采用的技術方案是按照以下步驟進行：

步驟一，將按需服務的數據包調度問題轉化為整數最優規劃問題；

1)建立時隙模型；

和表示網絡用戶進入和離開信息站h,h＝1,2,…,H的傳輸范圍的時刻，時間在每個間隔期間內被等分為時長T_F的時隙，第H信息站覆蓋的區域分為個時隙，用于數據傳輸的時隙總數確定在信息站每時隙內的最大數據包傳輸數量C_n,n＝1,2,…,N。

2)建立服務請求模型；

設用戶服務請求集合為S，S中的每個服務請求s(s∈S)表示為一個四元組：

(G_s,Q_s,D_s,W_s(n)) (1)

其中，Q_s為每個服務需要被調度的數據包數量，G_s為每個服務的到達時間，D_s為該服務的最晚調度時間，W_s(n)為收益，其中n為該數據包的發送時隙；如果該服務的請求在它的生命周期[G_s,D_s]內被調度，那么該請求的每一個數據包將會獲得一定收益，否則將不會獲得收益。

3)將問題轉化為求解最優整數規劃問題；

令x_ns表示請求s在時隙n內發送數據包的數量，則調度方案表示為向量該調度方案將調度產生的總收益表示為如下目標函數：

其中，

其中，(2a)表示，數據包只能在服務的生命周期內才能被調度和分配，超出生命周期的數據包無效，且被調度數據包的數量只能為整數；(2b)表示在每個時隙內調度的數據包數量不能超過該時隙能發送的數據包數量的上限；(2c)則表示每個服務被調度數據包的數量不能超過該服務需調度數據包數量的上限。

步驟二，將步驟一的整數最優規劃問題轉化為0-1最優規劃問題

基于時隙的容量，引入一種時隙到虛擬微時隙的映射。根據時隙n的容量C_n，該時隙被劃分成C_n個微時隙，每個微時隙的容量是1，即最多僅一個數據包可以在每個微時隙內調度傳輸；通過這種映射關系，N個時隙共產生個微時隙；經過映射后，服務s的到達時間G_s和最晚調度時間D_s分別轉化為：和令m表示微時隙的序號，x_ms表示微時隙m∈[g_s,d_s]內服務s傳輸數據包的數量，且x_ms∈{0,1}。

故步驟一的整數最優規劃問題被規約為下列0-1規劃問題，目標函數變為：

其中，

其限制條件含義和(2a)(2b)(2c)相似，唯一的區別在于(3a)，即每個微時隙最多只能發送一個數據包。

步驟三，根據新貪心策略采用貪心算法對該問題進行優化求解；

1)提出一種新的效用函數值作為新貪心策略：

其中α是可變的參數。

2)利用貪心算法求解式(3)，貪心算法具體步驟如下：

①初始化當前時隙序號n，可預測信息信道區間長度N_c，已經到達的服務集合S^*；

②對于根據(4)分別計算U_s；

③根據U_s值從大到小對S^*中的服務進行排序，獲得排序后集合其中

④利用新貪心策略在當前時隙區間內優先安排U_s值大服務的數據包，每安排一個數據包，信道可用容量減1，相應服務的待調度數據包的數量減1；

⑤根據步驟④中調度的結果更新服務集合S^*，對于數據包全部調度完成的服務從S^*中刪除，未調度完成的更新其尚未調度數據包數量；

⑥檢查服務集合是否全部到達完畢，到達完畢后根據實際調度結果計算總收益。

本發明的有益效果為：

基于該新貪心策略的貪心算法，仿真結果證明，比基于現有貪心策略的貪心算法更加高效，而且基于這種貪心策略的貪心算法和目前學者提出的online checker算法相比，仿真結果證明能夠獲得更大的總效益。

附圖說明

圖1為本發明整體流程圖。

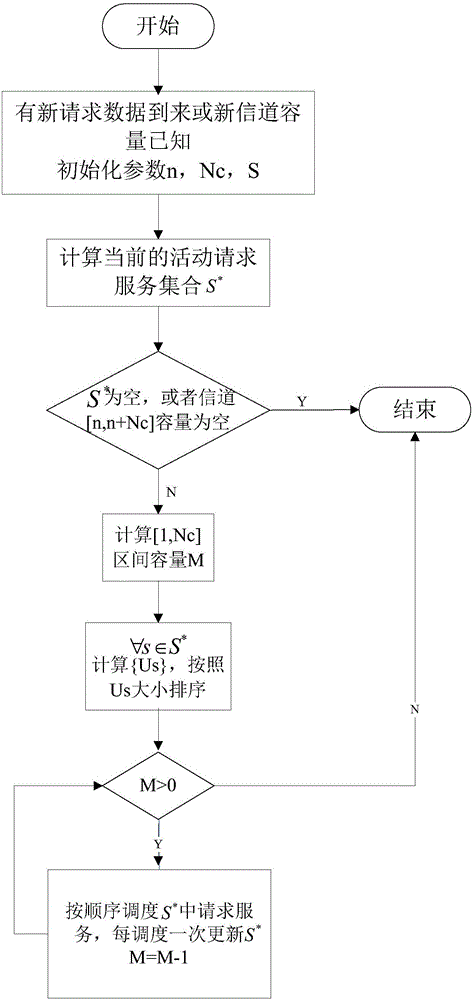
圖2為本發明的貪心算法流程圖。

圖3為時隙到微時隙的映射。

圖4為仿真效果圖。

具體實施方式

下面結合附圖和具體實施例對本發明的技術方案進行詳細說明。

實施例1：

給出一種新的按需服務的數據包調度算法，目的在于使得數據包調度獲得更大的收益，在online條件下，上述目標函數獲得更大值，如圖1所示。

步驟一，將按需服務的數據包調度問題轉化為整數最優規劃問題；

步驟二，將步驟一的整數最優規劃問題轉化為0-1最優規劃問題；

一個具體的時隙映射如附圖3所示。

步驟三，根據新貪心策略采用貪心算法對該問題進行優化求解；

Online條件下，假設當前時隙為n，未來N_c時隙的信息已知，即信道容量已知，且在當前時隙已經到達的待調度的請求服務集合為S^*已知，這樣基于現有的信息，應用貪心算法來解決。舉例來說，如圖2所示：

假設在時隙1到達的服務集合為S₁，在時隙區間[1,N_c]內的待調度服務集合(服務的生命周期內且待調度的數據包數量不為0)為S^*，明顯地，此時S^*＝S₁，在該調度區間內應用貪心算法解決直到新的服務請求到達或者新的信道信息已知。假設現在有新的請求集合S_n到達時隙n(n≤N_c)，這樣我們把時隙n“看作”新的時隙1，更新S^*：新到達的請求加入S^*，對于原來S^*中的請求，如果已經超出生命周期或者其數據包已經全部被調度，則從S^*中刪除，對于其他的請求，則更新它們的待調度數據包數量。不斷有新請求服務到來不斷重復上述過程，直到所有的請求服務全部被調度。

基于前面提出貪心策略，使用貪心算法來求解online條件下該問題的步驟如下：

1.初始化當前時隙序號n，可預測信息信道區間長度N_c，已經到達的服務集合S^*；

2.對于根據式(4)分別計算U_s；

3.根據U_s值從大到小對S^*中的服務進行排序，獲得排序后集合其中

4.利用貪心策略在當前時隙區間內優先安排U_s值大服務的數據包，每安排一個數據包，信道可用容量減1，相應服務的待調度數據包的數量減1；

5.根據步驟4中調度的結果更新服務集合S^*，對于數據包全部調度完成的服務從S^*中刪除，未調度完成的更新其尚未調度數據包數量；

6.服務集合是否全部到達完畢，到達完畢后根據實際調度結果計算總收益。

根據上述算法，將其程序化，利用matlab進行仿真實驗。實驗中，采用如下實驗樣本：每個時隙的容量為5，即每個時隙可以映射為5個微時隙，請求報文到達時間符合泊松分布，到達速率符合泊松分布，生命周期符合均值為10的指數分布,每個請求服務需要發送的數據包的數量Q_s滿足[5,15]的隨機分布，每個數據包的單價W_s滿足[1,10]的隨機分布。

基于以上的實驗數據，采用多次試驗取平均和均值的方法，每個算法做500次實驗取平均值，計算方差，繪制了仿真結果圖。

比較例1：

目前最流行的貪心策略是按照W_s進行貪心選擇，即優先調度報文單價W_s大的服務，W_s越大，其待調度優先級越高。這種貪心策略也是其他各種貪心策略的基礎，除此之外，其他學者還提出了兩種基于效用函數的貪心策略：Smith Ratio效用函數和Exponential Capacity效用函數。其中，請求服務s的Smith Ratio效用函數值定義如下：

U_s＝W_s/Q_s (5)

該效用函數的思路簡單，一個服務s的W_s越大或者需要發送的數據包的數量越少，那么s的效用值就越大。

請求服務s的Exponential Capacity效用函數值定義為：

其中，即當前時刻(時隙)已經到達的所有服務的集合，而表示s在當前時刻(時隙)還尚未調度的數據包的數量。仿真實驗結果顯示，利用該效用函數值作為貪心策略的貪心算法效果不如之前學者提出的online checker算法，而online checker算法已經被證明是解決該問題算法中較優的，考慮競爭比，在離線最優算法下，該算法的競爭比最低可以達到最優離線算法的1/2。

如圖4所示，基于該新貪心策略的貪心算法，仿真結果證明，比基于現有貪心策略的貪心算法更加高效，而且基于這種貪心策略的貪心算法和目前學者提出的online checker算法相比，仿真結果證明能夠獲得更大的總效益，相比于比較例中的兩種效用函數的貪心算法更加高效。