本發明屬于無線通信信號處理及神經網絡技術領域，尤其是涉及一種基于復合正弦混沌神經網絡的信號盲檢測方法。

背景技術：

數據通信和無線傳感網技術的迅猛發展，對通信信號的盲檢測(Blind Detection)提出了更高的要求。所謂盲檢測是指僅利用接受信號本身便能夠檢測出發送信號，從而消除符號間干擾(ISI)以提高信息傳輸速率和可靠性。

為解決遺傳、蟻群、免疫、粒子群等多種智能算法引起的容易陷入局部極小值且收斂速度慢的問題，許多文獻開始利用Hopfield神經網絡對信號盲檢測問題進行研究。Hopfield神經網絡(Hopfield Neural Networks,HNN)盲檢測算法不受信道是否含公零點的限制且所需發送數據更短，與二階統計量盲算法和高階統計量盲算法相比，更能滿足現代通信系統中高速數據傳輸的要求。文獻[張昀，現代通信系統與通信信號處理[PhD],博士學位論文(南京：南京郵電大學),2012.]論證了基于HNN的盲檢測算法研究已有初步成效，以及網絡趨向穩定平衡的充要條件。文獻[張昀，張志涌，于舒娟.基于幅值相位型Hopfield神經網絡的多進制振幅鍵控盲檢測[J].物理學報,2012,61(14):140701-1-140701-9.]提出了一種基于幅相型離散多電平激活復數Hopfield神經網絡(CHNN-APHM)的新算法，并分別在同步和異步更新模式下分析了新網絡的穩定性。文獻[阮秀凱,張志涌.基于連續Hopfield型神經網絡的QAM信號盲檢測[J].電子與信息學報,2011,33(7):1600-1605.]提出了一種使用連續Hopfield型神經網絡的多值平方QAM信號的盲檢測算法，并設計出一種與之相應的復數激活函數。然而，由于梯度下降的動力學特性，Hopfield神經網絡很容易陷入局部最小值，有時甚至不能得到全局最優或近最優解。因此，一些學者將混沌技術引入Hopfield神經網絡。為了獲取全局最優解，他們利用各態歷經性和混沌的隨機性避免網絡陷入組合優化問題的局部最小值。文獻[Luonan Chen,Kazuyuki Aihara,Chaotic simulated annealing by a neural network model with transient chaos[J].Neural Networks,1995，8(6):915–930]指出暫態混沌神經網絡(Transient Chaotic Neural Networks,TCNN)可以避免陷入局部最優。然而，TCNN具有負的自耦合，會導致能量函數的收斂速度變慢。針對這一問題，需要一種新的復合正弦混沌神經網絡，以改進復合正弦混沌神經網絡(ICSCNN)，使得它不僅具有較強的全局搜索能力且具有較高的搜索效率。

技術實現要素：

本發明為了克服現有技術的缺陷和不足，提供一種基于復合正弦混沌神經網絡的信號盲檢測方法。本發明方法在混沌神經網絡的基礎上加上時變增益參數函數和分段指數退火函數，既繼承了混沌神經網絡的優點又顯著改善了算法的收斂性能。該網絡旨在為無線通信網的信號盲檢測提供一種避免陷于局部最優解且收斂速度極快的算法，即準確且快速的信號盲檢測方法。

為解決上述技術問題，本發明所采用的技術方案是：

一種基于復合正弦混沌神經網絡的信號盲檢測方法，其特征在于，所述方法包括如下步驟：

步驟A，構造接收數據矩陣：

接收端接收單個用戶發送信號，經過過采樣，獲得離散時間信道的接收方程：

X_N＝SΓ^T

式中，X_N是接收數據陣，S是發送信號陣，Γ是由信道沖激響應h_j構成的塊Toeplitz矩陣；(·)^T表示矩陣轉置；

其中，發送信號陣：

S＝[s_L+M(k),…,s_L+M(k+N-1)]^T＝[s_N(k),…,s_N(k-M-L)]_N×(L+M+1)，

M為信道階數，L為均衡器階數，N為所需數據長度；

s_L+M(k)＝[s(k),…,s(k-L-M)]^T；其中，s∈{±1}，時刻k為自然數；

h_j＝[h₀,…,h_M]_q×(M+1)，j＝0,1,…,M；

q是過采樣因子，取值為正整數；

X_N＝[x_L(k),…,x_L(k+N-1)]^T是N×(L+1)q維的接收數據陣，

其中x_L(k)＝Γ·s_L+M(k)；

步驟B，接收數據矩陣奇異值分解：

式中，

(·)^H是Hermitian轉置；

U是奇異值分解中的N×(L+M+1)維的酉基陣；

0是(N-(L+M+1))×(L+1)q維的零矩陣；

V是(L+1)q×(L+1)q維的酉基陣；

U_c是N×(N-(L+M+1))維的酉基陣；

D是(L+M+1)×(L+1)q維的奇異值陣；

步驟C，設置權矩陣W＝I_N-Q，其中I_N是N×N維的單位陣，

其中，矩陣W為混沌神經網絡的權矩陣，且W＝W^H，矩陣W的第i行第j列的元素為w_ij，其對角元w_ii>0；

步驟D，選擇復合正弦混沌神經網絡的激活函數，進行復合正弦混沌神經網絡迭代運算；

所述復合正弦混沌神經網絡動態方程為：

y_i(t)＝σ^-1(x_i(t))

其中：

t為網絡迭代過程中運行的時間，該網絡中的連續時間t和離散時間k通過歐拉公式實現轉換；

x(t)為N個神經元的輸出構成的向量，t時刻，第i個神經元的輸出為x_i(t)，第j個神經元的輸出為x_j(t)；0≤i≤N，0≤j≤N；

σ^-1(·)表示Sigmoid激活函數σ(·)的反函數；

K′為神經元的衰減因子；

ε是耦合因子；

w_ij是第i神經元與第j個神經元間的連接權值；

I_i是第i個神經元的偏置；

z_i(t)為第i個神經元的自反饋連接權值；

λ為自反饋連接權值z_i(t)的衰減因子，且0<β₁<0.01、0<β₂<1；

對所述復合正弦混沌神經網絡動態方程進行迭代運算，然后把每次迭代的結果代入復合正弦混沌神經網絡的能量函數E(t)中，當該能量函數E(t)達到最小值，即S(k)＝S(k+1)時，該混沌神經網絡達到平衡，迭代結束；

步驟D中，所述改進的復合正弦混沌神經網絡的激活函數和時變增益參數分別為：

x_i(t)＝σ(y_i(t))＝sin(tan(u_i(t)×y_i(t)))

u_i(t+1)＝(1-γ)u_i(t)

其中，σ(·)表示Sigmoid激活函數，u_i(t)為第i個輸入神經元的時變增益參數，γ為時變增益參數的衰減因子，且0<γ<0.01；

步驟D中，所述復合正弦混沌神經網絡的能量函數為：

其中：

α為該網絡的尺度參數；

為第i個神經元的Sigmoid函數σ_i(τ)的反函數，τ為被積函數的自變量。本發明的有益效果是：本發明提出了一種基于復合正弦混沌神經網絡的信號盲檢測方法。所述方法采用復合正弦的混沌神經網絡和Sigmoid組合的非單調的激勵函數、時變的輸出函數增益和分段指數退火函數構成了一個復合正弦混沌神經網絡；每次迭代時，首先進入混沌神經網絡，然后再進入激活函數；所述混沌神經網絡具有可以避免陷于局部最小值。本發明方法繼承了混沌神經網絡這一特點，提高了盲檢測性能；并且，該網絡具有更加豐富靈活的暫態混沌動力學特性以及更強的全局搜索能力；在同等條件下，本發明的抗噪性能優于傳統的Hopfield信號盲檢測算法。

附圖說明

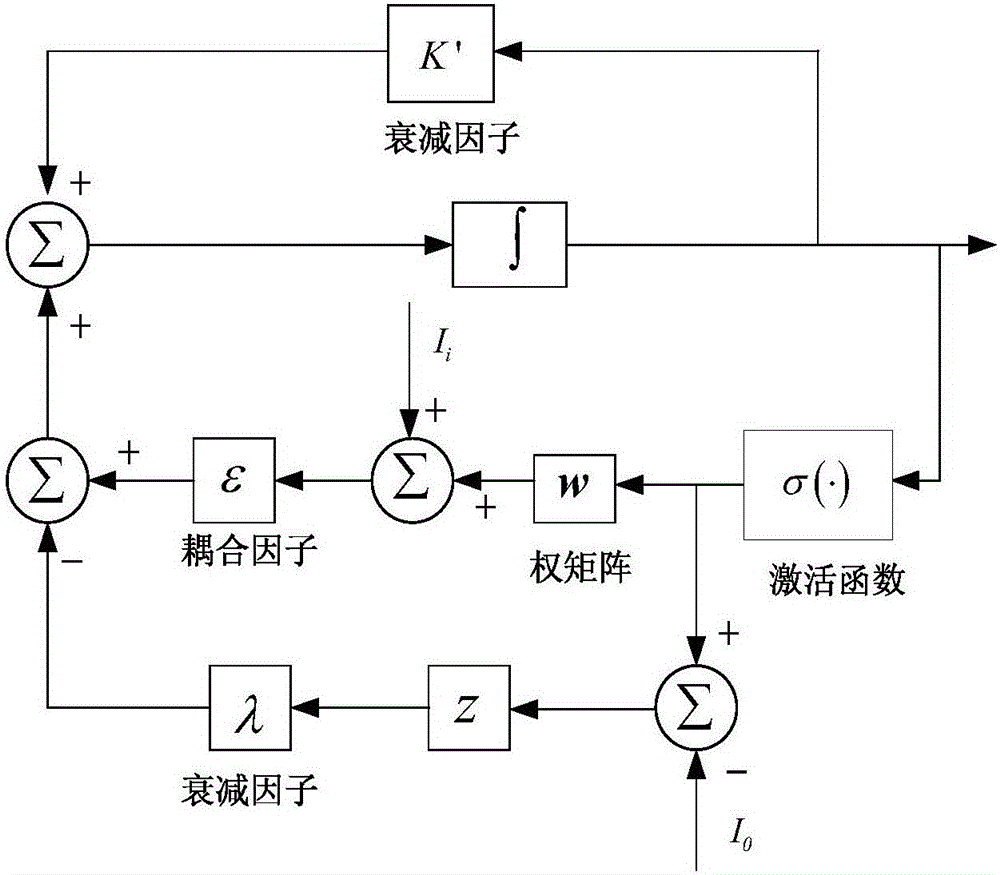
圖1本發明一種基于復合正弦混沌神經網絡的信號盲檢測方法系統機構圖。

圖2本發明一種基于復合正弦混沌神經網絡的信號盲檢測方法與暫態混沌神經網絡盲檢測算法單個混沌神經元的狀態演變圖。(a)TCNN(Transient Chaotic Neural Networks)算法為暫態混沌神經網絡算法，(b)ICSCNN(Improved Compound Sine Chaotic Neural Networks)算法為復合正弦混沌神經網絡算法。

圖3本發明一種基于復合正弦混沌神經網絡的信號盲檢測方法與暫態混沌神經網絡算法在采用權值和延時固定的合成信道下的誤碼率的比較圖。圖3(a)和圖3(b)為分別在同步更新模式和異步更新模式下的誤碼率曲線圖

具體實施方式

下面結合附圖，對本發明提出的一種基于復合正弦混沌神經網絡的信號盲檢測方法進行詳細說明：

一種基于復合正弦混沌神經網絡的信號盲檢測方法，其實施過程如下：

忽略噪聲時，離散時間信道的接收方程定義如下

X_N＝SΓ^T (1)

式中，X_N是接收數據陣，S是發送信號陣，Γ是由信道沖激響應h_j構成的塊Toeplitz矩陣；(·)^T表示矩陣轉置；

其中，發送信號陣：

S＝[s_L+M(k),…,s_L+M(k+N-1)]^T＝[s_N(k),…,s_N(k-M-L)]_N×(L+M+1)，

M為信道階數，L為均衡器階數，N為所需數據長度；

s_L+M(k)＝[s(k),…,s(k-L-M)]^T，其中s∈{±1}，時刻k為自然數；

h_j＝[h₀,…,h_M]_q×(M+1)，j＝0,1,…,M；

q是過采樣因子，取值為正整數；

X_N＝[x_L(k),…,x_L(k+N-1)]^T是N×(L+1)q維的接收數據陣，

其中x_L(k)＝Γ·s_L+M(k)；

對于式(1)，Γ列滿秩時，一定有滿足Qs_N(k-d)＝0，U_c是N×(N-(L+M+1))維的酉基陣，由奇異值分解中得到；

其中：

(·)^H是Hermitian轉置；

U是奇異值分解中的N×(L+M+1)維的酉基陣；

0是(N-(L+M+1))×(L+1)q維的零矩陣；

V是(L+1)q×(L+1)q維的酉基陣；

U_c是N×(N-(L+M+1))維的酉基陣；

D是(L+M+1)×(L+1)q維的奇異值陣；

據此構造性能函數及優化問題：

其中，s∈{±1}^N是N維向量，所屬字符集{±1}，表示信號的估計值。argmin()表示使目標函數取最小值時的變量值，d為延時因子，d＝0,…,M+L。如此，盲檢測問題就成為了式(3)的全局最優解問題。

圖1是本發明一種基于復合正弦混沌神經網絡的信號盲檢測方法系統結構圖。包含權矩陣模塊、激活函數、積分器、衰減因子和耦合因子。

a)該系統的動態方程為：

y_i(t)＝σ^-1(x_i(t))

(5)

其中，t為網絡迭代過程中運行的時間，該網絡中的連續時間t和離散時間k之間可以通過歐拉公式互相轉換。i代表第i個神經元，0≤i≤N；σ^-1(·)為神經元的激活函數的反函數；K′為輸入神經元y_i(t)的衰減因子，ε是耦合因子；w_ij是神經元y_j與y_i間的連接權值，I_i是第i個神經元的偏置，λ為自反饋連接權值z_i(t)的衰減因子且0<β₁<0.01、0<β₂<1。x(t)為N個神經元的輸出構成的向量，第i個神經元的輸出為x_i(t)，同理，第j個神經元的輸出為x_j(t)。該網絡達到最后平衡時，可近似的認為每個神經元的x_i(t)＝s_i(t)，x(t)即為求取的發送信號。

把復合正弦混沌神經網絡的激活函數和時變增益參數設計為：

x_i(t)＝σ(y_i(t))＝sin(tan(u_i(t)×y_i(t))) (7)

u_i(t+1)＝(1-γ)u_i(t) (8)

其中，σ(·)表示Sigmoid激活函數，u_i(t)為t時刻第i個輸入神經元的時變增益參數，γ為時變增益參數的衰減因子且0<γ<0.01。

b)能量函數

在圖1所示的采用式(4)、式(5)、式(6)描述的復合正弦混沌神經網絡中，若該網絡由N個神經元構成，權矩陣W＝W^H，矩陣W的對角元ω_ii＞0，該網絡衰減系數λ>0，激活函數σ(y_i(t))＞0，那么該神經網絡的能量函數表述為：

其中：E(t)為該網絡的能量函數，該能量函數是一個與迭代時間有關系的變量；α為該網絡的尺度參數；σ_i^-1(τ)為第i個神經元的Sigmoid函數σ_i(τ)的反函數，τ為被積函數的自變量；

綜上所述，該網絡每次循環都先進入混沌神經網絡結構跳出了局部極小點之后再進入激活函數，混沌神經網絡和激活函數就構成了一個復合正弦混沌神經網絡，既保證了網絡可以避免局部極小點又使得網絡的收斂速度加快，最后達到網絡的平衡。

為利用復合正弦混沌神經網絡實現信號盲檢測，求解式(2)、(3)的信號盲檢測問題，要使能量函數的最小值點對應于盲檢測性能函數的最小值點。由于歐拉公式可以使連續時間和離散時間之間進行相互轉換，在網絡達到穩定時，可近似認為x_i(t)＝s_i(t)，比較能量函數式(9)的第一部分與性能函數式(2)，則可看出相差一個負號，所以可考慮設計復合正弦混沌神經網絡的權矩陣為投影算子形式W＝I_N-Q，其中I_N是N×N維的單位陣，這樣就使能量函數E(t)的最小值點對應于盲檢測性能函數(2)的最小值點，從而能夠用復合正弦混沌神經網絡實現信號盲檢測。

圖2和圖3分別是本發明一種基于復合正弦混沌神經網絡的信號盲檢測方法的仿真實驗圖。這里的仿真采用不含公零點的經典文獻信道，發送信號為二進制相移鍵控信號，固定數據長度N＝100，噪聲為高斯白噪聲，所有仿真結果都經過100次蒙特卡洛實驗而得。

圖2是在條件相同的情況下，本發明算法與暫態混沌神經網絡盲檢測算法單個混沌神經元的狀態演變圖。圖3(a)和圖3(b)是本發明算法與暫態混沌神經網絡算法分別在同步更新模式和異步更新模式下的誤碼率曲線圖。圖中TCNN(Transient Chaotic Neural Networks)算法為暫態混沌神經網絡算法，ICSCNN(Improved Compound Sine Chaotic Neural Networks)算法為復合正弦混沌神經網絡算法。仿真圖表明：無論是在同步更新模式下還是在異步更新模式下，ICSCNN算法能量函數收斂速度明顯快于TCNN算法，并且ICSCNN算法的誤碼性能要明顯優于TCNN算法。