本發明屬于自適應陣列信號處理領域，具體涉及一種色噪聲環境下基于約束Kalman波束形成方法。

背景技術：

近年來，波束形成器被廣泛應用于無線通信、語音處理、雷達、聲納、醫學成像和其它領域。常見的波束形成器是最小方差無失真響應波束形成器(Minimum Variance DistortionlessResponse,MVDR)。MVDR算法是通過求解輸入信號的協方差矩陣進而求取陣列權值，該方法受到采樣快拍數的影響較大，當采樣快拍數小時，所求的估計協方差和真實協方差之間誤差較大，算法的性能下降甚至失效，并且MVDR的收斂速度比較慢。針對收斂速度問題，Kalman濾波算法被應用到波束形成器上，在文獻(C.A.Baird,Jr.Kalman-type processing for adaptive antenna arrays.IEEE Int.Conf.Common.(Minneapolis,MN),June 1974,pp.10G–1-10G-44.)中，Baird提出了將Kalman濾波器應用到平穩環境下求解自適應陣列天線的陣列權值上，但是要求輸出信號大小必須近似于期望信號，并且估計的不準確性會導致在觀測方向上信號的損失。為了解決這個問題，在文獻(Y.H.Chen,C.T.Chiang,AdaptiveBeamforming Using the Constrained Kalman Filter.IEEE Trans.AntennasPropag.vol.41,no.11,pp.1576-1580,Nov.1993.)中，Yuan-Hwang等人提出了基于約束Kalman下的自適應波束形成，該方法在原有的Kalman濾波算法的基礎上，添加一個沿著觀測方向的陣列響應約束到Kalman濾波算法的量測方程上，該算法可以實現非常快的收斂速度，并且能夠在干擾方向上形成零陷。Kalman濾波算法由于其高收斂速度和低失調量的優點，被廣泛應用到波束形成上。

但是以上波束形成器設計方法通常假定背景噪聲為白噪聲，但在應用中，實測數據表明，背景噪聲并不總是白噪聲而是色噪聲。在色噪聲環境下會導致波束形成算法波形畸變—旁瓣升高和主瓣下降或消失。文獻(ZHANG Linrang,LIAOGuisheng,and BAO Zheng.AdaptiveBeamforming in Colored No-ise Environment.ACTA E L EC TR ONI CA SINICA,1998,(12)：75-78.)提出了一種有色噪聲環境下克服波形畸變的自適應波束形成方法，但是該方法須知有色噪聲的特性。文獻(ZHANG Yi,YANGQiong,and TANG Chengkai.An Anti-jamming Algorithm for GPS Adaptive Nulling Antenna Based on Colored Loading[J].Journal ofNorthweaternPolytechnical University,2015，33(5)：874-878.)提出了基于有色對角載入的GPS自適應調零天線抗干擾方法，先對采樣協方差矩陣進行擴展，再根據濾波器權值矢量和方向矢量確定一個有色對角矩陣，對采樣協方差矩陣進行修改。以上方法都是針對有色噪聲下MVDR算法的改進，改進的算法只是能夠消除波形畸變，并不能提高算法的收斂速度。色噪聲環境下如何改進算法來消除畸變是一個需要解決的問題。

技術實現要素：

本發明的目的在于克服上述技術的缺陷，提出一種色噪聲環境下基于約束Kalman波束形成方法。

本發明的目的是這樣實現的：

(1)建立陣列天線接收信號模型；

(2)建立白噪聲環境下陣列接收數據的狀態方程和量測方程，并應用Kalman濾波五組方程，求解出白噪聲環境下陣列權矢量；

(3)對色噪聲進行一階馬爾科夫建模，將有色量測噪聲白化，并在此基礎上對陣列接收數據量測噪聲進行量測擴充；

(4)將色噪聲模型和擴充后的量測帶入到Kalman濾波五組方程中，得到新的Kalman濾波方程，最后求解陣列天線權矢量；

所述的步驟(3)包括以下步驟：

(3.1)對量測噪聲進行一階馬爾科夫建模，將有色量測噪聲白化，建立模型如下

V_m(k+1)＝ψ(k+1,k)V_m(k)+ζ(k).

上式中，相關系數ψ(k+1,k)＝exp(-βT)，β為反相關時間，T為采樣時間間隔，ζ(k)為零均值高斯白噪聲，并且與v_s(k)不相關；

(3.2)將量測有色噪聲白化，對量測矩陣進行擴充得到

Y＝B(k+1)^Hw(k+1)+ψ(k+1,k)V_m(k)+ζ(k).

上式中，B(k)^H為量測矩陣，V_m(k)為量測噪聲；將原來的量測方程進行變換得到V_m(k)＝Y-B(k)^Hw(k)，帶入到上式中得到

Y-ψ(k+1,k)Y＝[γB(k+1)^H-ψ(k+1,k)B(k)^H]·

w(k)+B(k+1)^Hv_s(k)+ζ(k).

若設則上式可以轉化成量測方程的標準形式

Z＝H(k)w(k)+n(k).

由上式可知，新的量測噪聲n(k)為高斯白噪聲，并且其協方差矩陣為R^*(k)＝E[n(k)n^H(k)]。

所述的步驟(4)包括以下步驟：

(4.1)將擴充后的新的量測方程帶入到Kalman濾波方程中可以得到新的權值更新方程

w(k+1)＝K(k+1)[Z-H(k)w(k+1|k)].

上式中，K(k+1)為Kalman濾波增益；

(4.2)求取濾波增益K(k+1)

K(k+1)＝P(k+1|k)H^H(k)[H(k)P(k+1|k)H^H(k)+R^*(k)]^-1.

上式中w(k+1|k)為狀態的一步預測，P(k+1|k)為一步預測方差陣；

(4.3)求取w(k+1|k)和P(k+1|k)；

w(k+1|k)＝γw(k).

P(k+1|k)＝γ²P(k)+Q.

其中P(k)為k時刻Kalman濾波方程的誤差方差陣；

(4.4)求取P(k+1)

P(k+1)＝[I-K(k+1)H(k)]P(k+1|k).。

本發明具有的有益效果在于：

本發明是在色噪聲環境下對波束形成算法的改進。將Kalman濾波算法應用到波束形成上，大大提高了收斂速度，同時低快拍數下波束形成算法波形畸變問題得到了一定的改善；對色噪聲進行一階馬爾科夫建模，并對量測矩陣擴充，最后帶入到Kalman濾波五組方程中得到新的濾波方程，最終求出陣列權矢量。本發明在低快拍數和色噪聲環境下能夠分別在期望信號和干擾方向上形成波束和零陷，并且波束圖的旁瓣相比原有的算法具有較為明顯的改進。

附圖說明

圖1是均勻線陣模型；

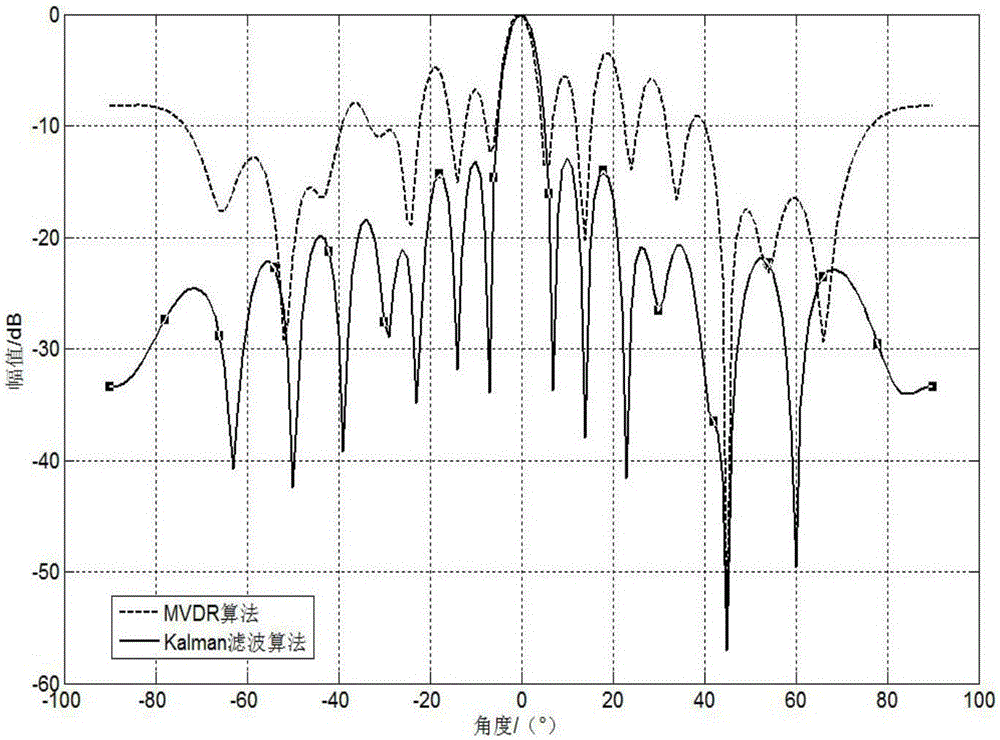
圖2是低快拍數下MVDR算法和Kalman濾波算法波束圖對比；

圖3是MVDR算法和Kalman濾波算法輸出SINR隨快拍數變化；

圖4是單干擾下有色噪聲下MVDR算法、Kalman濾波算法和本發明提出的算法的波束圖對比；

圖5是單干擾下有色噪聲下MVDR算法、Kalman濾波算法和本發明提出的算法的輸出SINR隨快拍數的變化；

圖6是三干擾下有色噪聲下MVDR算法、Kalman濾波算法和本發明提出的算法的波束圖對比；

圖7是三干擾下有色噪聲下MVDR算法、Kalman濾波算法和本發明提出的算法的輸出SINR隨輸入SNR的變化。

具體實施方式

下面結合附圖對本發明做進一步描述。

該方法首先利用約束Kalman的波束形成算法來提高收斂速度；其次對有色噪聲進行一階馬爾科夫建模，然后進行量測擴充后建立新的狀態方程和量測方程，最后根據擴展后的Kalman濾波方程組求取陣列權值矢量。本文提出的改進后的算法在低快拍數下仍能夠在期望信號方向上形成波束和干擾方向上形成零陷，并且對旁瓣有較好的抑制作用。

實現本發明目的技術方案：

色噪聲環境下基于約束Kalman波束形成方法，其特征在于：

步驟1：建立陣列天線接收信號模型；

步驟2：建立白噪聲環境下陣列接收數據的狀態方程和量測方程；并應用Kalman濾波五組方程，求解出白噪聲環境下陣列權值量；

步驟3：對色噪聲進行一階馬爾科夫建模，將有色量測噪聲白化，并在此基礎上對陣列接收數據量測噪聲進行量測擴充；

步驟4：將色噪聲模型和擴充后的量測帶入到Kalman濾波五組方程中，得到新的Kalman濾波方程，最后求解陣列天線權矢量。

步驟3中，具體包括以下步驟：

步驟3.1：對量測噪聲進行一階馬爾科夫建模，將有色量測噪聲白化，建立模型如下

V_m(k+1)＝ψ(k+1,k)V_m(k)+ζ(k).

步驟3.2：將量測有色噪聲白化，對量測矩陣進行擴充得到新的量測方程

Z＝H(k)w(k)+n(k).

步驟4中，具體包括以下步驟：

步驟4.1：將擴充后的新的量測方程帶入到Kalman濾波方程中可以得到新的權值更新方程

w(k+1)＝K(k+1)[Z-H(k)w(k+1|k)].

步驟4.2：求取濾波增益K(k+1)

K(k+1)＝P(k+1|k)H^H(k)[H(k)P(k+1|k)H^H(k)+R^*(k)]^-1.

步驟4.3：求取w(k+1|k)和P(k+1|k)。

w(k+1|k)＝γw(k).

P(k+1|k)＝γ²P(k)+Q.

步驟4.4：求取P(k+1)

P(k+1)＝[I-K(k+1)H(k)]P(k+1|k).

步驟1：建立陣列天線接收信號模型；

考慮M個陣元組成的均勻線陣，如圖1所示，假設陣元間各向同性并忽略陣元間互耦作用，陣元間距d為1/2λ，其中λ＝c/f，c為光速，f為入射信號的頻率。則接收信號模型可表示為

X(t)＝as(t)+j(t)+n(t). (1)

上式中，j(t)為干擾信號，n(t)為高斯白噪聲，s(t)為期望信號的大小，a為期望信號的導向矢量，可以寫成

a＝[e^{j2πdsinθ/λ}...e^{j2π(M-1)dsinθ/λ}]. (2)

假設期望信號和干擾信號互不相關并且都為平穩信號，則天線陣列所接收信號的協方差矩陣定義為

上式中，R_s＝E[s(t)s(t)^H]為期望信號的協方差矩陣，R_j為干擾的協方差矩陣，I為M維單位陣，為陣元噪聲功率，(·)^H代表矩陣共軛轉置。在實際中，上式的協方差矩陣無法獲得，可以根據信號的時間平穩特性，由采樣快拍數據得到其最大似然估計值，表示為

R_X＝X(t)X^H(t)/K. (4)

步驟2：建立白噪聲環境下陣列接收數據的狀態方程和量測方程，并應用Kalman濾波五組方程，求解出白噪聲環境下陣列權矢量；

針對傳統的波束形成器收斂速度慢的問題，將Kalman濾波器應用到波束形成上，大大提高了算法的收斂速度，并且穩態失調較小。

為了方便后面的推導，引進了輸出信號與零信號的均方差(MSE)，表示為

MSE＝E[|0-X^H(k)w(k)|²]＝w^HR_Xw. (5)

因此，使波束形成器輸出功率最小等價于使上式中MSE最小。同時波束形成器的約束函數可以表示為

st.w^Ha＝1. (6)

要利用Kalman濾波器來解決式(6)中陣列天線的約束函數，需要建立狀態方程和量測方程。波束形成器可以描述成陣列權值w滿足一階馬爾科夫過程的濾波器。因此陣列權值更新方程建立如下

w(k+1)＝γw(k)+v_s(k). (7)

上式中，γ式模型中的固定參數，v_s(k)為系統噪聲，假定為零均值高斯白噪聲，并且協方差矩陣為其中I為單位矩陣，下標“s”代表狀態方程。因此，式(7)給出了最優權值狀態方程。由式(6)中約束函數可以得到Kalman量測方程如下表示

上式可以寫成矩陣形式，表示如下

Y＝B(k)^Hw(k)+V_m(k). (9)

其中，Y＝[0 1]^T，量測矩陣可以表示為

量測噪聲可以表示為

其中v₁(k)和v₂(k)分別為殘余誤差和約束誤差，下標“m”表示量測方程，v₁(k)和v₂(k)均為零均值高斯白噪聲，其協方差矩陣可以表示為

在平穩環境下，由于最優約束權值矢量一直是一個常矢量，因此約束Kalman算法的真實模型過程方程，即一步預測方程可以表示為

w(k+1|k)＝γw(k). (13)

由式(13)和量測方程(9)可知，約束Kalman濾波算法最小化真實權值矢量與估計權值矢量之間的誤差并在觀測方向上保持無畸變。Kalman濾波算法的一步預測協方差矩陣記為

P(k+1|k)＝γ²P(k)+Q. (14)

Kalman濾波算法的估計權值矢量表示為

w(k+1)＝w(k+1|k)+K(k+1)[Y-B^H(k+1)w(k+1|k)]. (15)

上式中Kalman增益K(k+1)可以通過下式求取

K(k+1)＝P(k+1|k)B(k+1)[B^H(k+1)P(k+1|k)B(k+1)+R]^-1. (16)

其中用于計算一步預測協方差矩陣的濾波方差陣P(k)可以記為

P(k)＝[I-K(k)B^H(k)]P(k|k-1). (17)

上述參數中，γ和是狀態方程必須選定的參數，當外界環境發生變化時能夠按照系統模型變化求解最優權值，它們的功能可以從一步預測誤差方差陣看出，當這些參數增大時，Kalman濾波器給當前數據更大的權重，保證能夠更好的跟蹤環境。對于非平穩環境，γ值的典型選取為稍微比1大的值。盡管這個值的選取使狀態方程(7)不平穩，但是濾波器的觀測環境的平穩性可以通過觀測條件保證。的典型值一般選取這也就是說權值的每個元素的變化范圍為0.01。這里說明一下，的值越大，表明環境的變化越迅速。對于平穩環境來說，最優權值不隨時間發生變化，因此，在這種情況下，可以選擇γ＝1，

從量測方程的第一行可以得到，的選取必須同陣列天線的最優輸出功率的規則相同，后者的功率可以粗略的估計為σ²和分別為期望信號和入射信號中噪聲功率。w為波束形成器的最優權值矢量。值得我們注意的是波束形成器對的選取并不敏感，主要原因是，權值矢量范數的選取是由濾波器選擇的，因此波束形成器的輸出功率是與的值是相匹配的。但是的取值必須選擇很小(比如，)，這樣的話，系統的穩健性具有較高的精度。

上述算法中，系統噪聲v_s(k)和量測噪聲V_m(k)均假設為高斯白噪聲，但是在實際應用中，許多系統的干擾和量測噪聲均為有色噪聲，此時應用Kalman濾波算法求解波束形成器的陣列權值并不是最優的權值，并且與最優權值存在誤差，會導致算法性能下降甚至不能形成波束。

步驟3：對色噪聲進行一階馬爾科夫建模，將有色量測噪聲白化，并在此基礎上對陣列接收數據量測噪聲進行量測擴充；

步驟3.1：對量測噪聲進行一階馬爾科夫建模，將有色量測噪聲白化，色噪聲模型；

在原有的Kalman濾波算法的基礎上，對系統進行分析，可以得到陣列天線模型系統中的輸入的有色噪聲可以等價于量測噪聲，為保證量測噪聲始終為白噪聲序列，在應用Kalman濾波方程之前必須預白化有色噪聲V_m(k+1)。通過對量測噪聲進行一階馬爾科夫建模，將有色量測噪聲白化，建立如下模型

V_m(k+1)＝ψ(k+1,k)V_m(k)+ζ(k). (18)

其中相關系數

ψ(k+1,k)＝exp(-βT). (19)

式(19)中，β為反相關時間，T為采樣時間間隔，式(18)中ζ(k)為零均值高斯白噪聲，并且與v_s(k)不相關。

步驟3.2：將量測有色噪聲白化，對量測矩陣進行擴充得到新的量測方程；

量測有色噪聲白化常用的處理方法為觀測增廣法(差分法)，通過增廣觀測矩陣Y，量測矩陣B(k)^H和量測噪聲V_m(k)，將式(9)中的量測方程轉化成新的量測方程。將(18)式代入(8)式可得

Y＝B(k+1)^Hw(k+1)+ψ(k+1,k)V_m(k)+ζ(k). (20)

由量測方程(9)式可得

V_m(k)＝Y-B(k)^Hw(k). (21)

將上式代入(20)式中可得

Y-ψ(k+1,k)Y＝[γB(k+1)^H-ψ(k+1,k)B(k)^H]w(k)+B(k+1)^Hv_s(k)+ζ(k). (22)

若設(22)式被轉化成量測方程的標準形式

Z＝H(k)w(k)+n(k). (23)

由上式可知，新的量測噪聲n(k)為高斯白噪聲，并且其協方差矩陣為

R^*(k)＝E[n(k)n^H(k)]

＝E{[B(k+1)^Hv_s(k)+ζ(k)][B(k+1)^Hv_s(k)+ζ(k)]^H}

＝B(k+1)^HQ(k)B(k+1)+R_ζ. (24)

步驟4：將色噪聲模型和擴充后的量測帶入到Kalman濾波五組方程中，得到新的Kalman濾波方程，最后求解陣列天線權矢量。

步驟4.1：將擴充后的新的量測方程(23)和狀態方程(7)帶入到Kalman濾波方程中可以得到新的權值更新方程

w(k+1)＝K(k+1)[Z-H(k)w(k+1|k)]. (25)

上式中K(k+1)為Kalman濾波增益。

步驟4.2：求取濾波增益K(k+1)

K(k+1)＝P(k+1|k)H^H(k)[H(k)P(k+1|k)H^H(k)+R^*(k)]^-1. (26)

(25)式中w(k+1|k)為狀態的一步預測，(26)式中P(k+1|k)為一步預測方差陣。

步驟4.3：求取w(k+1|k)和P(k+1|k)。

w(k+1|k)＝γw(k). (27)

P(k+1|k)＝γ²P(k)+Q. (28)

上式中P(k)為k時刻Kalman濾波方程的誤差方差陣，描述的是真實的陣列權值和估計得到的陣列權值的誤差的大小。

步驟4.4：求取P(k+1)

P(k+1)＝[I-K(k+1)H(k)]P(k+1|k). (29)

由以上方程可以求得基于有色噪聲下的Kalman濾波波束形成器的陣列權值，該陣列權值的求取過程中考慮了有色噪聲對陣列權值的影響，波束形成器的性能能夠得到一定程度上的改善。

下面將所提的色噪聲環境下基于約束Kalman算法與現有的MVDR算法和約束Kalman算法比較，比較這些算法的在色噪聲環境下的性能。

相比現有的MVDR算法，Kalman濾波算法由于本身具有很快的收斂速度，能夠使算法輸出迅速達到收斂。但是在色噪聲環境下，無論是Kalman濾波算法還是MVDR算法，都會出現波形畸變問題-主瓣偏移和旁瓣上升，算法的性能下降。本專利提出的方法，考慮到色噪聲對算法性能的影響，對色噪聲進行建模，然后對Kalman濾波方程進行擴充，從根本上解決了色噪聲對算法性能的影響。因此本專利提出的方法相比其它兩種算法在色噪聲環境下的性能更優。

本發明的效果可通過以下仿真說明：

(一)仿真條件與內容：

1、低快拍數下波束形成器的性能分析

由于空間媒介不均勻等因素的原因，導致信號在傳播過程中出現損失，可以用一個方差為0.04的高斯白噪聲來修正。假設信號傳播過程中的噪聲為高斯白噪聲，均值為0，方差為0.04。并且選取γ＝1，P(0)＝αI,其中α值為常值，w(0)＝0，

圖2是在低快拍數Kalman濾波算法和傳統的MVDR算法的輸出波束圖。從圖中可以看出，在快拍數為30時，MVDR算法的輸出波束圖中主瓣有略微偏移并且旁瓣發生嚴重的升高。而采用Kalman濾波算法不僅能夠在干擾方向上形成較深的零陷而且還能夠在期望方向上形成較好的主波束。因此我們可以得到，在低快拍數下，MVDR算法的性能下降，而Kalman濾波算法仍然具有較好的性能。

圖3是兩種算法隨著快拍數不同輸出信干噪比(SINR)的變化，從圖中可以看出兩種算法最終的輸出SINR幾乎相同，但是Kalman算法在迭代次數較少時，輸出SINR仍然較高，并且在快拍數10以內時仍然具有較高的輸出SINR為-10dB左右。在快拍數變換范圍內Kalman濾波算法的輸出SINR幾乎保持穩定，而MVDR算法在快拍數低于40左右時，輸出SINR值隨快拍數變化迅速，在低快拍數時輸出SINR可以達到較低值-24dB，在快拍數為50時達到穩定值為-10dB左右。因此可以得出在低快拍數下，MVDR的算法性能受到很大的影響，但是當迭代次數增加時，算法的性能也在隨之增加，但是當快拍數達到一定值時，算法的輸出SINR保持不變；而Kalman濾波算法在快拍數為10左右時就已經達到穩定，輸出的SINR幾乎不隨快拍數發生改變。因此，從算法穩定性和收斂速度來看，Kalman濾波算法都具有一定的性能優勢。

從以上的仿真中我們可以得到，利用基于Kalman濾波下的波束形成算法能夠有效地提高算法的收斂速度，在快拍數為十幾次時算法就已經達到穩定，并且算法的性能相比MVDR算法來講，具有一定的優勢。因此，可以利用基于Kalman濾波下的波束形成算法來提高低快拍數下算法的收斂速度。

2、低快拍數和色噪聲環境下的波束形成器的性能分析

仿真中輸入信號噪聲選取有色噪聲，參數值的選取γ＝1，P(0)＝αI,其中α值為常值，w(0)＝0，有色噪聲一階馬爾科夫系數為ψ(k+1,k)在仿真中為常值。

圖4是在有色噪聲環境下，三種算法：本文所提出的算法，Kalman濾波算法和MVDR的波束圖。從波束圖中我們可以得到，在有色噪聲環境條件下，MVDR算法雖然能夠在干擾方向上形成零陷，但是不能在期望方向上形成波束，并且波束圖中旁瓣增益上升；Kalman濾波算法雖然能夠在干擾方向上形成零陷，也能夠在期望方向上形成主波束，但是主波束和旁瓣峰值的差距較小，旁瓣增益明顯上升，算法的性能有所下降；而本文提出的改進的算法不僅能夠形成主波束，并且能夠降低旁瓣增益，并且在干擾方向上還能形成零陷。從以上仿真結果圖可以得到，本文提出的改進的算法在有色噪聲環境下系統的性能可以得到很大的改善，明顯優于Kalman濾波算法和MVDR波束形成算法。

圖5是對改進的算法的輸出SINR的仿真圖，從圖中可以看出，在有色噪聲環境下，本文提出的算法最終的輸出SINR為-16dB左右，并且在迭代次數較少時，輸出SINR就已經達到穩定；而Kalman濾波算法的最終輸出SINR為-22dB左右，并且在20次迭代以后輸出SINR趨于穩定，MVDR算法的最終輸出SINR為-23dB左右，并且在60次迭代以后輸出SINR趨于穩定。從而可以得出本文的算法在有色噪聲環境下輸出SINR相比其他兩種算法較高，并且達到穩定所需的迭代次數更少。

圖6是三干擾有色噪聲下算法的波束圖，從圖中可以看出，三種算法均能夠在干擾方向上形成較深的零陷，但是MVDR算法和Kalman濾波算法不能夠在期望方向上形成波束，并且旁瓣相對較高，而本文提出的算法能夠在期望方向上形成主波束，并且有效的抑制了旁瓣增益。因此，從此圖中可以得出，在三個干擾情況下，本文所提出的算法相比其他兩種算法性能較好。

圖7是輸出SINR隨輸入SNR的變化，從圖中可以得出SINR隨著SNR變化近似成線性變化，并且相比MVDR算法和Kalman濾波算法來說，本文提出的算法在相同的SNR時，輸出SINR較大，從側面說明了本文算法的優越性。