本發明涉及信息安全技術領域，涉及網絡流量異常檢測方法，具體是一種基于相對熵理論的網絡流量異常檢測方法。

背景技術：
：

隨著計算機網絡規模的不斷擴大以及各類網絡應用的不斷深化，互聯網已經融于人類的生產生活，逐漸成為人們生活的一部分，在給人們生活帶來巨大方便的同時，網絡擁擠和網絡濫用等流量偏離其正常行為的流量異常情況時有發生，這些異常事件發作突然，并引起網絡流量的劇烈變化，給網絡安全和網絡性能造成極大的傷害。而異常檢測作為一種可以有效檢測網絡流量異常的方法，相關研究早已被廣大學者和業界人士所重視，并取得了一定的研究成果。

熵是一種源于熱力學的無序度量，表示系統微觀狀態的分布幾率。信息熵則是熵在信息系統中的一種擴展，如果將信息源視為一組隨機事件的集合，則熱力學中微觀狀態的混亂度類同信息源的隨機性不確定度，將熱力學幾率擴展到信息源信號出現的幾率，就是信息熵。信息熵是對信息系統中隨機事件不確定性程度的描述，標志著所含信息量的多少，信息熵作為一種復合型特征(區別簡單特征，如計數特征、流量特征等)，可以反映簡單統計特征無法反映的內涵。當網絡特征全部相同，取一個值時，表示特征的分布最集中，此時信息熵值取得最小值；當網絡特征全取不同值時，表示特征的分布最為分散，信息熵值取得最大值，擴展到網絡流量數據中，即在同一屬性上，數據分布越集中的地方信息熵值越小，數據分布越分散的地方信息熵值越大。據研究發現，使用信息熵進行計算時，源/目的ip、源/目的端口和流持續時間等特征分布要比其他特征分布效果更好，并且這些特征本身具有強相關關系，可以有效的表征大規模網絡流量的異常。以拒絕服務攻擊(distributeddenialofservice，簡稱ddos)為例，它借助足夠數量的傀儡主機，隨機偽造大量的ip地址，在幾乎同一時間開展拒絕服務攻擊，向目標主機發送大量無用分組，引起源ip地址的分布更加分散，進而造成源ip地址信息熵突然增大，目的地址信息熵突然減小。

基于信息熵的網絡流量異常檢測依賴于流量的特征分布，可以提供比傳統流量分析更細粒度的見解，近些年來引起了許多研究者的廣泛關注。andersen、nychis等人針對網絡流量報頭特征和行為特征分布，測量出不同分布的熵在時間序列上的成對相關得分，結果表明基于熵的異常檢測方法中，ip地址和端口分布之間具有強相關性，其他特征顯示低相關性或無相關性；berezińskip、pawelecj等人通過捕獲不同的流量特征，采用基于分組和基于流的方法，利用shannon熵和titchener熵以及參數化的renyi熵和tsallis熵四種信息熵算法分別實驗，研究證明，當特征分布選擇正確時，基于熵的檢測方法優于大部分傳統的異常檢測方法，其中ip地址和端口以及持續時間的特征分布是最好的選擇；國防科技大學教授鄭黎明、鄒鵬等針對傳統異常檢測系統分類器不同網絡環境下不斷變化的問題，提出了在hash直方圖上基于增減式的在線svdd流量異常檢測方法，結合多窗口關聯檢測算法結構，對提高分類器的檢測效果和檢測精度及減少算法的復雜度有很大的效果,但該方法需要大量的系統開銷，且有一定的難度；清華大學信息網絡工程研究中心專家朱應武和楊家海等通過對網絡流量信息結構和網絡流量規律的研究分析，利用正常網絡流量的ip、端口等具有重尾分布和自相似特性等穩定的流量結構的特點，結合信息熵理論，對流量進行建模，將網絡流量異常檢測問題轉換為基于svm的分類決策問題，提出了一種基于熵的支持向量機(supportvectormachine,svm)方法，實驗結果表明，基于信息熵的svm方法更加簡潔、高效，在網絡流量小樣本情況下，具有較高的檢測效率和良好的檢驗精度，但在應對大規模突發性流量方面有一定的缺陷；西安理工大學張亞玲博士等人提出通過對網絡流量進行統計分析，引入相對熵理論，通過對相對熵值多測度加權計算作為網絡異常判斷的依據，實現基于相對熵理論的網絡異常檢測，結果表明，該方法具有較低的誤報率，但檢測率效果不理想，而且需要計算大量的歷史數據，另一方面，加權系數的設定比較困難；中國民航大學馮興杰教授等人針對現有方法中模型彈性較差，無法適應動態網絡變化的問題，在hurst指數分析的基礎上，結合ewma和滑動窗口模型，提出一種基于動態閾值的網絡異常檢測，僅針對滑動窗口內的歷史觀測值進行分析，有效的避免了檢測效率低的問題，但只對突發性流量具有較好的檢測效果，對異常的類型檢測方面也有不足。

技術實現要素：

本發明的目的是針對現有技術的不足，而提供一種基于相對熵理論的網絡流量異常檢測方法。這種檢測方法能有效地檢測出網絡流量異常，并能解決低檢測率和高誤報率的問題，且能夠適應動態變化的網絡環境。

實現本發明目的的技術方案是：

一種基于相對熵理論的網絡流量異常檢測方法，包括如下步驟：

1)收集網絡流量數據：從原始網絡數據流中讀取所需的網絡流源端口的數據；

2)計算網絡流量信息熵值：網絡流量數據當作為離散信息源，將數據的特征當作一組隨機事件，定義隨機變量x＝{ni，i＝1，2，...，n},表示網絡流量數據中待分析的網絡特征i發生了ni次，xi則表示該特征的具體值，那么信息熵的定義如下：

ni/s表示x取值特征值xi的概率，表示當前檢測的網絡特征發生的總次數，

設檢測粒度為t，對檢測粒度t內的網絡流源端口的數據分布進行統計，將得到的統計結果通過公式(1)求出每個t內網絡流源端口的數據分布的信息熵值，得到網絡流源端口的數據分布情況的原始信息熵值序列e＝{ei，i＝1，2，...，m}，為下一步的檢測分析準備數據；

3)構建滑動窗口模型：設數據流為一個不斷增長的多維元組集合對任意各元組時標為t1...tj...，且對任意i＜m，ti＜tm，在滑動窗口模型中，在任意時刻只考慮并處理最近到達的n個元組，最近到達的n個元組稱為有效元組；其余的元組則稱為過期元組，并不再參與下一步的分析處理；

4)計算滑動窗口內信息熵值的平均值:本方法中采用網絡流量數據作為元祖集合的基本元祖。滑動窗口模型內預設w個正常網路流量數據，當有新的正常網絡流量數據時，滑動窗口向前推移，加入最新的正常流量數據，并剔除最舊的正常流量數據；滑動窗口模型在任意時刻，僅僅考慮并處理包含在模型內的最近到達的w個數據，包含在滑動窗口內的w個數據即為有效元祖，有效元祖時標前的數據，稱為過期元祖，且不參與數據的分析處理，正常信息熵值序列為ez＝{ezj，j＝1，2，...，n}，滑動窗口內包含最新的w個數據,求滑動窗口內數據的均值avg，其中

5)計算當前網絡流量的相對熵值：信息熵是表示對不確定性程度的一種度量形式，當流量有異常發生時，網絡流量在相關屬性的信息熵值會與正常歷史流量在該屬性的信息熵值發生顯著的差異性變化，對于這種差異性的變化，可以采用相對熵進行度量，相對熵，又稱k-l散度，用信息量d(p,q)表示，用來度量兩個概率分布p＝{p1，p2，...，pn}和q＝{q1，q2，...，qn}的相似程度，可表示為：

在信息熵的基礎上，相對熵可以表示為對同一屬性在不同狀態下的特征分布的信息熵值比，用信息量i(p,q)表示，結合信息熵公式，相對熵可表示為：

其中，p代表當前檢測的網絡流量分布，q代表正常的歷史網絡流量分布，h(p)和h(q)分別代表當前檢測的網絡流量分布的信息熵值和正常的歷史網絡流量分布的信息熵值，相對熵值i(p，q)的一個重要性質是：i(p，q)≥0恒成立，且根據定義，i(p，q)越接近1，表示p和q越接近，反之則表示兩個分布之間相差較大；當i(p，q)＝1時，表示兩個分布完全相同，此時，設u、v為上下限閾值，如果

i(p，q)∈[u，v](4)

則判定當前檢測的網絡流量正常；反之，則判定當前檢測的網絡流量發生異常，結合步驟4)，當前信息熵值h(p)為ei，正常的歷史網絡流量分布的信息熵值h(q)為avg，根據公式(3)，則相對熵值ei＝ei/avg，若ei∈(u，v),則判定為正常；否，判定為異常；

6)檢測下一粒度網絡流量是否異常：

(1)若當前檢測相對熵值無異常，將對應信息熵值放入正常信息熵值序列ez，滑動窗口向前推移一項，加入最新的正常熵值為活動數據，并剔除滑動窗口內最原始的一項為過期數據的活動數據，重新計算平均信息熵值avg，更新原有的avg，之后，跳轉至步驟4)，進行下一熵值的流量檢測；

(2)若當前檢測熵值為異常，則保持滑動窗口內數據、當前正常信息熵值的平均值avg不變，直接跳轉至步驟4)，進行下一熵值的異常檢測。

所述檢測粒度t為至少100。

所述網絡特征i為源或目的ip、源或目的端口。

在實際應用中，人們常常關心的是最近一段時間的信息情況而不是所有的數據信息情況，這是因為久遠的數據對最后的結果影響力比較小，而且在網絡環境中，“正常流量”并非一個特定的狀態，而是會隨著網絡環境以及相關因素的變化而不斷更新的狀態，因此，對于異常流量的判斷也必須基于當前網絡狀態的正常基準值來確定。

這種檢測方法將信息熵在原有的基礎上，加以延伸，采用相對熵與滑動窗口結合的方法對網絡流量進行異常的檢測，檢測率是指正確檢測的異常數目占實際異常數目的百分比；誤報率是指錯誤檢測的異常數目占檢測異常數目的百分比。

現實中，網絡流量是隨著網絡環境以及相關因素的變化而不斷更新的，比如，凌晨這個時段用戶少，網絡流量小，而工作時間等用網高峰期，網絡流量大，這就給異常的檢測帶來偏差影響，針對這種情況，通過滑動窗口模型內的有效數據和當前檢測數據相對熵值的變化可以準確的掌握當前數據流的狀態，保證檢測率的同時，有效降低誤報率。

這種檢測方法以信息熵算法為基礎，與滑動窗口相結合，吸收相對熵的理論思想，通過對網絡流量特征進行分析研究，建立熵值序列，結合滑動窗口模型，通過相對熵進行最后的檢測。

這種檢測方法能有效地檢測出網絡流量異常，并能解決低檢測率和高誤報率的問題，且能夠適應動態變化的網絡環境。

附圖說明

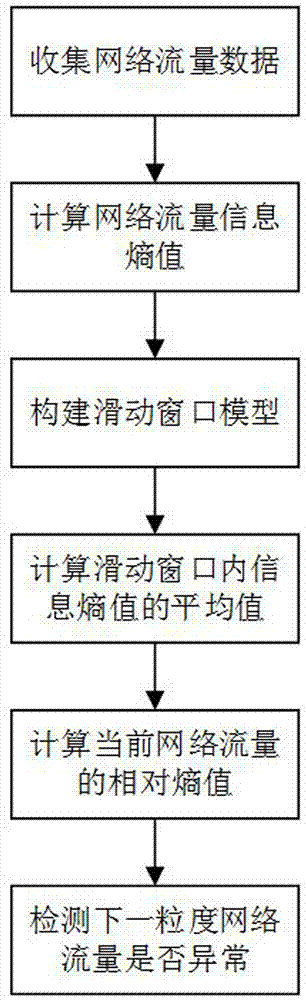
圖1為實施例的方法流程示意圖；

圖2為實施例中滑動窗口參數取值變化對應的檢測率和誤報率曲線示意圖；

圖3為實施例中上下閾值參數取值變化對應的檢測率和誤報率曲線示意圖；

圖4為實施例中檢測率與誤報率變化曲線示意圖。

具體實施方式

下面結合附圖和實施例對本發明內容作進一步的闡述，但不是對本發明的限定。

實施例：

參照圖1、一種基于相對熵理論的網絡流量異常檢測方法，包括如下步驟：

1)收集網絡流量數據：從原始網絡數據流中讀取所需的網絡流源端口的數據；

2)計算網絡流量信息熵值：網絡流量數據當作為離散信息源，將數據的特征當作一組隨機事件，定義隨機變量x＝{ni，i＝1，2，...，n},表示網絡流量數據中待分析的網絡特征i發生了ni次，xi則表示該特征的具體值，那么信息熵的定義如下：

ni/s表示x取值特征值xi的概率，表示當前檢測的網絡特征發生的總次數，

設檢測粒度為t，對檢測粒度t內的網絡流源端口的數據分布進行統計，將得到的統計結果通過公式(1)求出每個t內網絡流源端口的數據分布的信息熵值，得到網絡流源端口的數據分布情況的原始信息熵值序列e＝{ei，i＝1，2，...，m}，為下一步的檢測分析準備數據；

3)構建滑動窗口模型：設數據流為一個不斷增長的多維元組集合對任意各元組時標為t1...tj...，且對任意i＜m，ti＜tm，在滑動窗口模型中，在任意時刻只考慮并處理最近到達的n個元組，最近到達的n個元組稱為有效元組；其余的元組則稱為過期元組，并不再參與下一步的分析處理；

4)計算滑動窗口內信息熵值的平均值:本方法中采用網絡流量數據作為元祖集合的基本元祖。滑動窗口模型內預設w個正常網路流量數據，當有新的正常網絡流量數據時，滑動窗口向前推移，加入最新的正常流量數據，并剔除最舊的正常流量數據；滑動窗口模型在任意時刻，僅僅考慮并處理包含在模型內的最近到達的w個數據，包含在滑動窗口內的w個數據即為有效元祖，有效元祖時標前的數據，稱為過期元祖，且不參與數據的分析處理，正常信息熵值序列為ez＝{ezj，j＝1，2，...，n}，滑動窗口內包含最新的w個數據,求滑動窗口內數據的均值avg，其中

5)計算當前網絡流量的相對熵值：信息熵是表示對不確定性程度的一種度量形式，當流量有異常發生時，網絡流量在相關屬性的信息熵值會與正常歷史流量在該屬性的信息熵值發生顯著的差異性變化，對于這種差異性的變化，可以采用相對熵進行度量，相對熵，又稱k-l散度，用信息量d(p,q)表示，用來度量兩個概率分布p＝{p1，p2，...，pn}和q＝{q1，q2，...，qn}的相似程度，可表示為：

在信息熵的基礎上，相對熵可以表示為對同一屬性在不同狀態下的特征分布的信息熵值比，用信息量i(p,q)表示，結合信息熵公式，相對熵可表示為：

其中，p代表當前檢測的網絡流量分布，q代表正常的歷史網絡流量分布，h(p)和h(q)分別代表當前檢測的網絡流量分布的信息熵值和正常的歷史網絡流量分布的信息熵值，相對熵值i(p，q)的一個重要性質是：i(p，q)≥0恒成立，且根據定義，i(p，q)越接近1，表示p和q越接近，反之則表示兩個分布之間相差較大；當i(p，q)＝1時，表示兩個分布完全相同，此時，設u、v為上下限閾值，如果

i(p，q)∈[u，v](4)

則判定當前檢測的網絡流量正常；反之，則判定當前檢測的網絡流量發生異常，結合步驟4)，當前信息熵值h(p)為ei，正常的歷史網絡流量分布的信息熵值h(q)為avg，根據公式(3)，則相對熵值ei＝ei/avg，若ei∈(u，v),則判定為正常；否，判定為異常；

6)檢測下一粒度網絡流量是否異常：

(1)若當前檢測相對熵值無異常，將對應信息熵值放入正常信息熵值序列ez，滑動窗口向前推移一項，加入最新的正常熵值為活動數據，并剔除滑動窗口內最原始的一項為過期數據的活動數據，重新計算平均信息熵值avg，更新原有的avg，之后，跳轉至步驟4)，進行下一熵值的流量檢測；

(2)若當前檢測熵值為異常，則保持滑動窗口內數據、當前正常信息熵值的平均值avg不變，直接跳轉至步驟4)，進行下一熵值的異常檢測。

所述檢測粒度t為至少100，本例為100。

所述網絡特征i為源或目的ip、源或目的端口。

具體地：

本實施例采用迄今為止網絡安全審計研究人員使用最多的10％數據集(kddcup.data_10_percent_corrected)為實驗的研究分析對象，檢測粒度t為100，

對檢測率dr和誤報率fa定義如下：

dn，na，fd，df分別代表正確檢測出的異常數目、實際存在的所有異常數目、誤檢測為異常的正常數據數目，檢測的異常數目；

通過不斷的調整u、v、w三個實驗參數值對實驗進行測試，并對結果進行分析，結果如圖2-圖4所示；

經過大量的實驗測試發現，圖2中，當u、v一定時，隨著滑動窗口w的增大，模型的檢測率先增加后減小，之后增加并穩定在區間[0.9,1]上,而誤報率則隨著w值的增大，先減小后增加，在圖3中，隨著對u、v、w三個參數值的不斷調整，模型的檢測率和誤報率整體呈現增大趨勢，當dr＞0.936時，模型的檢測率提升速度逐漸減慢，但誤報率的增長速度加大，檢測率和誤報率的關系曲線如圖4所示。在保證誤報率在可接受范圍內，檢測率越高越好的前提下，綜合分析可知，當檢測率設在區間0.886～0.936之間時，檢驗結果比較理想，此時誤報率在0.05～0.08之間，

通過分析測試結果可知，當相對熵上限值u＝3.6，相對熵下限值取v＝0.394時，dr＝0.935，fa＝0.055，結果相對理想，對kddcup9910％數據集(kddcup.data_10_percent_corrected)進行檢測，結果如表1所示：

表1檢測結果

由表1可知，本實施例的方法針對數據集中包含的四種異常類型均能有效的檢測出來，其中以dos攻擊檢測結果最為優秀，檢測率為97.8％，probe、u2r和r2l的檢測率分別為78.74％、61.54％和75.84％，整體檢測結果達到預期的效果。

為了證明實驗改進的有效性，表2給出了3種不同網絡流量異常檢測的方法的結果，a代表一種基于分析視圖的相對熵異常檢測方法；b代表一種基于信息熵的異常檢測方法；c代表基于信息熵的改進的k-maens網絡流量異常檢測方法；d代表本實施例方法：

表2不同檢測方法異常檢測結果比較

對比表中不同方法檢測結果可知：檢測率方面，方法a＜b＜c＜d，誤報率方面，方法b＞c＞d＞a；相對于方法a、b、c三種算法，本實施例方法的檢測率比方法a高出了8.5％，比方法b高出了2.3，比方法c高出0.8％；誤報率方面，本實施例的方法比方法a高出0.5％、比方法b低3.1％、比方法c低1.96％。

綜合分析表明，本實施例的方法在信息熵與相對熵理論的基礎上，結合滑動窗口技術，采用最近影響力較大的正常流量數據，動態更新相對熵值，對網絡流量進行異常檢測，在保證低誤報率的同時，最大限度提高了檢測率，在總體上，對異常檢測的性能有很大的改進。