本發明屬于無線通信技術領域，設計了高速鐵路運行中，基于蜂窩信息站集成網絡的無線網絡環境下，一種基于kuhn-munkres算法的收益率時間相關服務數據包的調度算法。

背景技術：

本文應用一種基于蜂窩信息站集成的三層網絡架構，即內容服務器，信息站(路邊通信單元)和車輛站，系統中的網絡數據服務方式為按需服務方式。這種網絡架構和服務方式現在已經廣泛應用于服務高速列車乘客的網絡需求和v2x車聯網系統通信中。在該系統中，蜂窩網絡基站通過穩定的有線網絡連接與內容服務器相連，提供較低速的網絡信號覆蓋；信息站部署在軌道旁，能夠提供小范圍較大數據傳輸速率的網絡接入。信息站和蜂窩網絡集成的網絡系統，能夠綜合蜂窩網絡和信息站各自的優點。

當車載設備(用戶)按照需求請求數據服務時，數據報文將通過路邊信息站與車載設備或終端(手機，電腦等)之間的無線信道將數據調度和分配給用戶。高速鐵路乘客(網絡用戶)通過蜂窩網絡鏈路請求按需服務數據，服務數據從主干網絡傳遞到信息站，然后再傳輸給車輛站。最后，車輛站(部署在高速列車上)負責分配調度數據包給車廂內部用戶的終端設備。信息站通過穩定的有線網絡鏈路連接到主干網絡核心服務器，車輛站到用戶終端設備的連接可以由wi-fi等高速無線局域網技術負責實現。服務數據傳遞到用戶設備后，服務的確認信息由車輛站經由信息站最終由蜂窩集成網絡進行傳輸。

為了滿足車輛在高速行駛過程中基站與車輛通信的需求，克服多普勒效應等對網絡通信的影響，有學者提出一種專門用于基站與車載設備通信的mac幀結構。這種結構下，每個時間區間被分為時間間隔相等的用于信息傳播的時隙，時間間隔小于信道相干時間(channelcoherencetime)，劃分的每個時隙的信道增益是固定的，但是由于信號衰減等原因，時隙的容量會因不同的情況而有所差異。考慮時隙中信道增益等信道信息，每個時隙可以發送的數據包數量上限可以確定。

考慮按需數據調度的質量和用戶良好的網絡體驗，高質量、低延遲、低丟包率等要求是在線調度數據包時要追求的目標。同時，在按需請求數據服務下，用戶愿意為不同的服務付出的代價也是不同，另外由于用戶之間的差異，不同用戶愿意為請求服務支付的價格也不相同。在高速鐵路環境下，由于信道狀態不太穩定，以及種種因素，尤其是多普勒效應的限制，數據由信息站到車輛站的調度是整個網絡傳輸的瓶頸，因此，怎樣合理高效利用信道，合理調度服務數據，使得調度的服務數據獲得最大價值，讓服務運營商或提供者獲得最大收益是很重要的目標。本發明所解決的目標問題就是如此。

1.系統模型

本文所述問題中的時隙模型如下，高速鐵路沿線信息站總數為h，假設每個信息站覆蓋范圍不重疊。和表示車輛進入和離開信息站h,h＝1,2,…,h覆蓋范圍的時刻。如上述背景技術所述，時間在每個時間間隔內被劃分為相等時長為tf的時隙，則第h信息站覆蓋的時間可以分為時隙，則用于數據傳輸的時隙總數為其中時隙n內數據包傳輸容量為cn,n＝1,2,…,n。

按需請求的數據模型如下，用戶服務請求集合為s，對于s中的每個服務s∈s，使用一個四元組(gs,qs,ds,ws(n),ls(n))來定義，其中：

(1)s在傳輸過程中將被編碼為長度固定的數據包，每個服務需要被調度的數據包最大數量為qs；

(2)服務的到達時間為時隙gs，可以被調度的最晚時間為時隙ds；

(3)如果該服務請求的一個數據包在其生命周期[gs,ds]之間的時隙n內被調度，將獲得收益ws(n)；

(4)每個請求s在時隙n內可以被調度數據包的數量上限為ls(n)。

2.目標問題

基于上述時隙模型和請求模型，該按需數據調度問題被轉化為整數最優規劃問題。每個服務數據待調度的數據包只有在該請求服務的生命周期之內被調度才會產生效益，即令xns表示請求s在時隙n內發送的數據包的數量，則一種調度方案可以表示為向量所以，目標函數可以表示為：

約束條件為

其中，條件(1a)表示數據包只能在服務的生命周期內才能被調度和分配，超出生命周期的數據包無效，且被調度數據包的數量只能為整數；(1b)表示在每個時隙內調度的數據包數量不能超過該時隙能發送的數據包容量；(1c)則表示每個服務被調度數據包的數量不能超過該服務需要調度最大數據包數量；(1d)表示每個請求在一個時隙內分配的數據包的數量不能超過上限。

上述問題由于約束條件(1a)，該整數規劃問題是一個np困難問題，在多項式時間內不能找到最優解。考慮上述時隙的特殊結構，采取一種基于每個時隙可發送數據包容量的“虛擬微時隙”的映射，可以將這個問題轉化為相對容易求解的0-1最優規劃問題。

根據時隙n的容量cn，該時隙被劃分成的cn微時隙，微時隙容量是1，即最多僅一個數據包可以在微時隙被調度傳輸。通過這種映射關系，n時隙共產生微幀。經過映射后，請求s的請求時間gs和截止時間ds分別轉化為：和請求s的生命周期內時隙的個數為k,k＝ds-gs+1，對于請求s的生命周期內每個時隙k，bsk為其映射后的第一個微時隙，esk為映射后的最后一個微時隙。

以m表示微時隙的序號，xms表示微時隙m內服務數據s傳輸數據包的數量。由于微時隙只能傳輸一個數據包，所以xms∈{0,1}。

故上述整數最優規劃問題被等效規約為下列0-1規劃問題，目標函數為：

約束條件為

其約束條件含義和(1a)(1b)(1c)相似，唯一的區別在于(2a)，即每個微時隙最多只能發送一個數據包。

3.基于加權二分圖的最大權匹配算法：kuhn-munkres算法。

二分圖可以表示為g(x,y,e)，它的頂點可以分類兩個集合x和y，所有的邊關聯在兩個頂點中，恰好一個屬于集合x，另一個屬于集合y，且帶有權值w(x,y)。

匈牙利算法是基于hall定理中充分性證明的思想，它是二分圖匹配最常見的算法，該算法的核心就是尋找增廣路徑，它是一種用增廣路徑求二分圖最大匹配的算法。

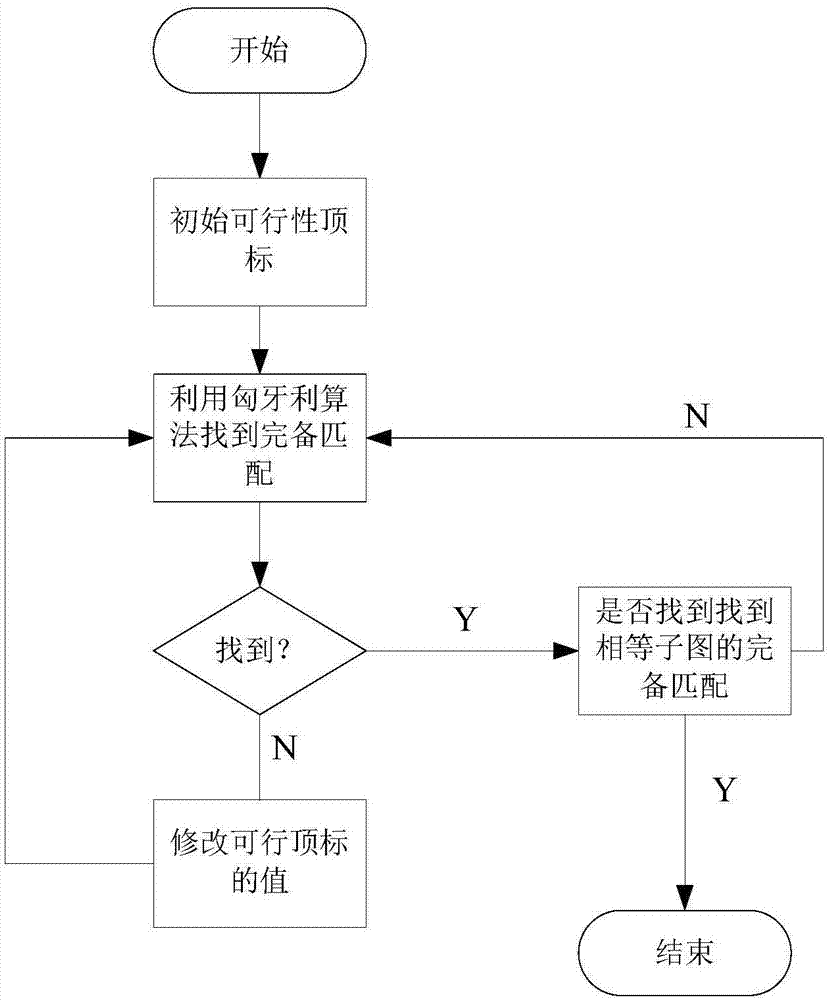
kuhn-munkres算法的具體步驟如下：

1)初始化可行頂標的值；

2)用匈牙利算法尋找完備匹配；

3)若未找到完備匹配則修改可行頂標的值；

4)重復2)3)直到找到相等子圖的完備匹配為止。

技術實現要素：

本發明為了解決按需請求數據調度問題，達到效用最大化，提出了一種基于kuhn-munkres算法的收益率時間相關服務數據包的調度算法。

具體技術方案如下：

在線環境下，假設當前時隙為n，信道一次建立包括nc時隙，即nc時隙的信息(信道容量)已知，當前時隙已經到達的待調度的請求服務集合為s^*。

本文所采用的技術方案是按照以下步驟進行：

步驟一，建立服務請求模型，按照請求模型將問題轉化為上述調度問題；

將服務請求表示為一個五元組：

(gs,qs,ds,ws(n),ls(n))(3)

其中，每個服務需要被調度的數據包數量為qs，其到達時間為gs，截止時間為ds，如果該服務的請求在時隙n∈[gs,ds]內被調度，那么該請求的每一個數據包將會獲得收益ws(n)，每個請求s在時隙n內可以被調度數據包的數量上限為ls(n)；

步驟二，將在線調度問題轉化為加權二分圖，并使用鄰接矩陣存儲；

將待調度請求數據的待分配數據包作為二分圖g(x,y,e)的一個頂點集合x，已知信息時隙經過微時隙映射后產生的微時隙作為頂點集合y；現有的一個簡單的轉化規則是，當請求數據s中的任意待調度數據包在一個微時隙m內調度，滿足gs≤m≤ds，則在該數據包和微時隙之間存在一條邊，這樣的轉化規則不能滿足限制條件(2d)，對轉化規則做出改進，當時隙n滿足gs≤n≤ds，該請求s的每個數據包與時隙n內的ls(n)個微時隙相連，即請求s的每個數據包與時隙n有且僅有ls(n)條邊，且保證該請求s的所有數據包在每個時隙n內連接的微時隙是相同的；該邊的權值為該數據包在該微時隙m中分配能夠獲得收益值ws(m)。

在數據結構的層面就將“每個請求在時隙內調度的數據包的數量不能超過某個上限”這個限制條件滿足。

改進的轉化完成以后，因此將在二分圖層面上滿足約束條件(2d)，將轉化后的加權二分圖用鄰接矩陣存儲表示。

步驟三，基于步驟二存儲為鄰接矩陣形式的加權二分圖，利用kuhn-munkres算法求解，得到最優匹配。

本發明的有益效果為，針對提出的新問題(2)，應用基于kuhn-munkres算法的在線調度算法，能夠取得較好的效果，達到效益的近似最優化。由于目前針對上述新問題尚無專門的新算法出現，根據仿真實驗結果分析，新提出的算法比之前解決類似問題的經典算法在提高總收益方面有明顯的優勢。

基于kuhn-munkres算法的在線調度算法至少能夠達到離線最優算法的90％以上，且相比于傳統貪心算法、指數容量算法和先進先出算法的優勢較為明顯：對于指數容量算法，大概有20-30％的性能領先，而相比于先進先出算法，其領先優勢更加明顯，大約有40％。相比于貪心算法，也是要優于貪心算法的。而且新提出的算法可以作為之后學者研究提出算法的標桿和對照。

附圖說明

圖1為kuhn-munkres算法流程圖；

圖2為本發明的算法流程圖；

圖3為仿真效果圖；

圖4為按照簡單規則轉化的二分圖；

圖5為修改轉化策略后轉化的二分圖。

具體實施方式

下面對本發明的實施方式進行詳細說明。

實施例1

3個時隙信息已知，每個時隙的信道容量均為5，2個待調度請求，其中：s1＝(1，3，8，3，2),s2＝(4，4，12，4，3)。認為ws(n)和ls(n)均為常數，且圖中沒有畫出。s1需要有3個數據包待調度，s2有4個數據包待調度，于是按照簡單轉化規則轉化后的二分圖和修改規則后轉化的二分圖如附圖4和附圖5所示。

在線條件下，假設當前時隙為n，未來nc時隙的信息已知，即信道容量已知，對于請求數據s，qns表示其在時隙n到達時剩余的待調度數據包的數量。

步驟一，計算當前的已經到達的請求集合s^*＝{s∈s|gs≤n≤ds,qns＞0}，并更新s^*中元素的生命周期；

對于新到達的請求數據s^new，其到達時間為截止時間為對于在n時隙之前就已到達的且滿足qns＞0的數據s，更新其截止時間為min{n+nc,ds}，更新待調度的數據包數量qs＝qns。

假設在時隙1到達的服務集合為s1，在時隙區間[1,nc]內的待調度服務集合(服務的生命周期內且待調度的數據包數量不為0)為s^*，明顯地，此時s^*＝s1；假設現在有新的請求s^new到達時隙n(n≤nc)，把時隙n“看作”新的時隙1，更新s^*：新到達的請求s^new加入s^*，更新其到達時間對于原來s^*中的請求，如果已經超出生命周期或者其數據包已經全部被調度，則從s^*中刪除，對于其他的請求，則更新它們的待調度數據包數量。

步驟二，將上述在線調度問題轉化為加權二分圖；

將目前待調度請求數據的待分配數據包作為二分圖g(x,y,e)的一個頂點集合x，目前已知信息時隙經過微時隙映射后產生的微時隙作為頂點集合y；當請求數據s中的任意待調度數據包在一個微時隙m內調度，滿足gs≤m≤ds，則在該數據包和微時隙之間存在一條邊。這樣的轉化措施不能滿足問題的限制條件，于是對轉化規則做出改進，即必須滿足對于時隙n(gs≤n≤ds)，該請求數據s的每個數據包與時隙n的微時隙都有且只有ls(n)條邊相連，且保證一個請求的所有數據包在每個時隙內連接的微時隙是相同的。該邊的權值為該數據包在該微時隙m中分配能夠獲得收益值ws(m)。這樣，在數據結構的層面就將“每個請求在時隙內調度的數據包的數量不能超過某個上限”這個限制條件滿足。

轉化后的加權二分圖用鄰接矩陣存儲表示；然后，基于該二分圖的鄰接矩陣，使用kuhn-munkres算法求解。

步驟三，基于上述改進的加權二分圖，利用kuhn-munkres算法求解。

上述問題轉化為加權二分圖，并存儲為鄰接矩陣的形式，利用kuhn-munkres算法，求解最優匹配，該最優匹配僅僅是原問題的一個近似最優解。

實施例2

在仿真實驗中，設置有總時隙數量n：30～100，列車中無線用戶產生的按需請求的到達速度(請求個數/時隙)服從平均速率為3的泊松分布，每個請求的生命周期為10個時隙，每個請求包含的待調度數據包數量服從[5,15]的隨機分布，每個請求的每個數據包支付的價格服從[1,10]的隨機分布，信道一次建立包含時隙的數目(nc)是10。仿真效果圖如圖3所示。