本發明屬于光學設計技術，涉及一種實現光子晶體光纖與實心光纖低損耗熔接的方法。
背景技術：
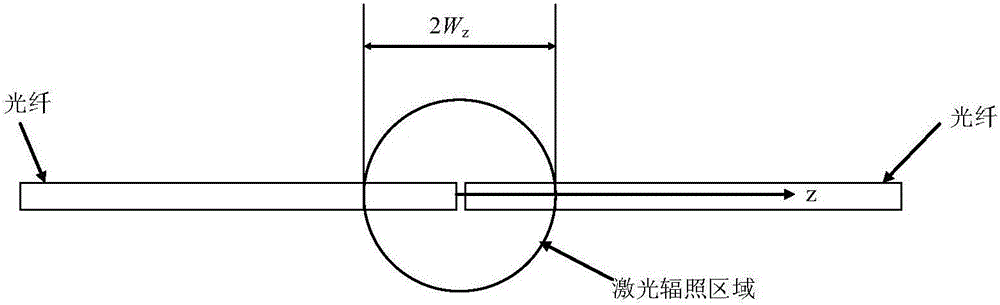
：光子晶體光纖(PhotonicCrystalFiber，PCF)或稱為微結構光纖(Micro-StructureFiber，MSF)，是近十幾年出現的一種新型光纖，與常規實心光纖有顯著區別的新型特種光纖。這種結構的光纖沿光線軸向方向有規律地分布著許多空氣孔，改變空氣孔的大小和排列方式，將會改變輸出光的特性，這種特有的特點使它有望研制出各種新穎的光電子器件，特種光纖，因此光子晶體光纖將會廣泛應用于光通信和光電子領域。但在開發研究這些應用時，都涉及光子晶體光纖的連接技術，目前可通過光纖活動連接器、電弧放電熔接方式、二氧化碳激光器熔接方式進行光子晶體光纖與普通實心光纖之間的連接。而二氧化碳激光器熔接方式以其高吸收率(波長10.6um)，激光的形狀和能量可控，無如染和殘留物等優勢成為光子晶體光纖與普通實心光纖熔接的首選方式。然而一方面由于光子晶體光纖與普通實心光纖結構、物理參數都存在差異，同時光子晶體光纖存在的特殊空氣孔結構的存在，在對二氧化碳激光器放電加熱過程中，會出現與普通實心光纖溫升、溫度分布情況、熔融情況不一致的現象影響熔接損耗；另一方面可通過匹配光子晶體光纖與普通實心光纖模場來減小熔接損耗，而光子晶體光纖有效模場面積取決于熔接完成后的光子晶體光纖空氣孔結構。因此，必須通過對放電加熱過程中的溫度場分布數值分析與仿真，研究出一套控制光子晶體光纖空氣孔結構參數的方法，精確實現兩側光纖熔融的同時，控制光子晶體光纖空氣孔塌陷程度使兩種光纖有效模場達到最佳匹配，從而使熔接損耗降低至最小。技術實現要素：本發明的目的：提供一種通過控制光子晶體空氣孔塌陷程度，實現光子晶體光纖與實心光纖低損耗熔接的方法。本發明的技術方案：一種實現光子晶體光纖與實心光纖低損耗熔接的方法，其通過建立光子晶體光纖與普通實心光纖熔融狀態下的溫度場分布模型以及空氣孔受力模型，模擬放電過程中兩側光纖溫度變化情況以及空氣孔壁受力情況，進而推導出空氣孔塌陷程度與二氧化碳激光器放電參數之間的數值關系，再通過建立光子晶體光纖端面結構與其有效模場面積的數值關系，得到光子晶體光纖與實心光纖熔接的損耗模型，進而精確計算出實現低損耗熔接的二氧化碳激光器放電參數。二氧化碳激光器放電參數包括放電中心位置、放電時間、放電量。所述的實現光子晶體光纖與實心光纖低損耗熔接的方法，其具體步驟如下：步驟1：建立兩側光纖有效模場面積與熔接損耗模型光子晶體光纖的高雙折射特性是由其中心附近兩個大圓的幾何結構形成的，根據光的電磁理論計算，光被束縛在光纖中心時，電場強度分布光子晶體光纖中心的電場強度分布E1；同時計算普通實心光纖纖芯中的電場分布E2；高雙折射型光子晶體光纖和熊貓保偏光纖耦合時，在突變界面將發生模式轉換，其中一部分與波導的模式相匹配，將繼續在波導中傳播；另一部分與波導的模式不匹配，變成輻射模而損失掉，損失掉的這部分能量成為耦合失配損耗，通過兩波導的模式匹配計算耦合效率，進而可以建立兩側光纖有效模場面積與熔接損耗的模型；步驟2：光子晶體光纖導熱特性分析對光子晶體光纖受熱的導熱特性進行分析，得到不同二氧化碳激光器放電參數下光子晶體光纖溫度場分布模型；步驟3：光子晶體光纖與普通實心光纖熔接時導熱特性分析結合步驟2光子晶體光纖溫度場分布模型，進行光子晶體光纖與普通實心光纖熔接時的導熱特性分析，進而建立不同二氧化碳激光器放電參數下兩側光纖的溫度場分布模型；步驟4：光子晶體光纖與普通實心光纖熔接時力學特性分析結合步驟3不同二氧化碳激光器放電參數下的兩側光纖溫度場分布模型，建立熔融狀態下光子晶體光纖粘度系數與溫度的關系和光子晶體光纖流動方程，根據光子晶體光纖中氣液兩相界面的流動過程，使用氣液兩相流中的水平集方法對其石英-空氣界面進行追蹤，得到石英液體界面在表面張力下運動方程，進而建立不同二氧化碳激光器放電參數下光子晶體光纖空氣孔結構模型；步驟5：建立二氧化碳激光器放電參數與熔接損耗的數值模型結合步驟4不同二氧化碳激光器放電參數下光子晶體光纖空氣孔結構模型，以及步驟1光子晶體光纖與普通實心光纖有效模場面積與損耗模型，建立二氧化碳激光器放電參數與熔接損耗的數值關系；步驟6：低損耗熔接參數確定結合步驟5二氧化碳激光器放電參數與熔接損耗的數值模型，為了得到最低的熔接損耗，即需要實現兩側光纖模場的最佳匹配，求得熔融狀態下光子晶體光纖空氣孔結構，進而可以推導出要得到上述結構需要的二氧化碳激光器放電參數：放電量、放電時間、放電中心位置。在放電時間確定時，放電中心位置delta可由公式(1)得出z＝-419.6delta2-0.945delta+7.943×10-5(7)其中，Z為光纖端面軸向坐標。放電量在確定放電時間下，由z＝0位置處，溫度與放電時間的關系曲線確定。在確定放電時間下，z＝0位置處，溫度與放電時間的關系曲線，由如式(8)所示的二氧化硅粘度系數μ確定其中，T為與放電時間相關的溫度。光子晶體光纖空氣孔的塌陷程度影響塌陷面積，從而影響光纖耦合，兩側光纖在突變界面將發生模式匹配時的光纖耦合效率，由公式(5)確定，其中，E1(x，y)和E2(x，y)分別為兩側光纖在突變界面的兩個模場分布。本發明的優點和有益效果是：通過建立光子晶體光纖與普通實心光纖熔融狀態下的溫度場分布模型以及空氣孔受力模型，模擬放電過程中兩側光纖溫度變化情況以及空氣孔壁受力情況，進而推導出空氣孔塌陷程度與二氧化碳激光器放電參數(放電中心位置、放電時間、放電量)之間的數值關系，通過兩側光纖有效模場面積與熔接損耗的數值模型推導出冷卻后光子晶體光纖有效模場直徑，進而精確計算出二氧化碳激光器的放電參數(放電中心位置、放電時間、放電量)。這樣一方面可以在熔接操作實施前精確計算出能使兩側光纖同時達到熔融狀態，且最高溫度點出現在界面處的二氧化碳激光器放電參數，避免具體生產操作過程中操作失敗帶來的損失，減少返工；另一方面可以通過對二氧化碳激光器放電參數的精確計算，可以控制光子晶體光纖空氣孔結構，使光子晶體光纖與普通實心光纖在熔融狀態時的有效模場達到最佳匹配狀態，進而使冷卻后熔接損耗降至最低。附圖說明圖1是光子晶體光纖電場有效模式的等值線圖；圖2是二氧化碳激光器加熱被熔光纖示意圖；圖3是氧化碳激光器加熱光子晶體光纖示意圖；圖4是t＝300ms兩側光纖的溫度分布曲線；圖5是在溫度和表面張力作用下導致空氣孔塌陷的光子晶體端面示意圖；圖6是粘度與溫度的關系曲線；圖7端面溫度與時間關系曲線；圖80.5s時空氣孔的收縮情況；圖9收縮前后模型對比；圖10收縮后光子晶體光纖模式。具體實施方式下面結合附圖對本發明作進一步的說明：本發明實現光子晶體光纖與實心光纖低損耗熔接的方法通過建立光子晶體光纖與普通實心光纖熔融狀態下的溫度場分布模型以及空氣孔受力模型，模擬放電過程中兩側光纖溫度變化情況以及空氣孔壁受力情況，進而推導出空氣孔塌陷程度與二氧化碳激光器放電參數之間的數值關系。再通過建立光子晶體光纖端面結構與其有效模場面積的數值關系，得到光子晶體光纖與實心光纖熔接的損耗模型，進而精確計算出實現低損耗熔接的二氧化碳激光器放電參數。具體過程包括如下步驟：步驟1：建立兩側光纖有效模場面積與熔接損耗模型光子晶體光纖的導光特性是由中心附近的數層空氣孔決定的，其高雙折射特性是由其中心附近兩個大圓的幾何結構形成的。根據光的電磁理論，利用有限元的方法，由下式為基礎可以分析光子晶體光纖的模式。εr＝(n-jk)2(3)其中，E是電場強度，k0為真空中波數，εr為相對介電常數，β為傳播常數，n為折射率。(1)式為亥姆霍茲方程，(2)式為將電場的z分量分離，(3)式為折射率與相對介電常數和波數的關系。根據(2)式，可將(1)式轉化為x,y平面上的電場方程。根據(3)式，可將(1)式轉化為與折射率相關的方程。光在進入光纖時，包含許多模式，每一個模式與相應的有效折射率對應。由于光纖結構的限制，只有特定的模式可以存在。因此，使用有限元方法對光子晶體光纖材料折射率附近的有效折射率進行篩選，即可得到可在纖芯中傳播的模式，傳播模式在端面上的電場分布為E1(x，y)，如附圖1所示。對于熊貓型單模保偏光纖，光強在橫截面內的分布為高斯型，若模場直徑為2ω(在1/e2光強處)，高斯光束的模場分布表示為：高雙折射型光子晶體光纖和熊貓保偏光纖耦合時，在突變界面將發生模式轉換，其中一部分與波導的模式相匹配，將繼續在波導中傳播；另一部分與波導的模式不匹配，變成輻射模而損失掉，損失掉的這部分能量成為耦合失配損耗，因此可得到其耦合效率η為：步驟2：光子晶體光纖導熱特性分析激光具有高單色性、高相干性、高方向性和高亮度的特點，它是一種理想的熱、光能源。二氧化碳激光的波長為10.6um，其光子能量為0.176eV，遠小于化合物的電離能，不能直接導致化合物發生化學反應。二氧化碳激光器的工作模式為TEM00，光束為高斯分布，光斑為圓形，激光輻照區與光纖之間相對位置示意圖如附圖2所示。激光輻照度為其中，Ptotal為總功率，Wy，Wz分別為二氧化碳激光器光束照射形成的圓形光斑y，z場的半徑。由于實心PCF的材料是二氧化硅，其熔點為(1700±5)K，熔接光子晶體光纖既要求熔接區域的溫度能夠達到熔點，又不能夠太高，以免造成空氣孔的塌陷，而且為了得到熔接質量較好的光子晶體光纖，需要纖芯和包層同時達到熔點。由傳熱學理論可知，只要橫截面包層與纖芯的溫差小于1％，就可以認為它們達到了統一的溫度。另外，由于激光能量在光纖長度方向呈高斯分布，對光纖溫度場進行三維仿真，研究光子晶體光纖中空氣孔的效應和對熔接條件的控制。附圖3所示為利用二氧化碳激光器加熱光子晶體光纖的實驗裝置示意圖，圖中z＝0的位置即光子晶體光纖的左端面位于激光輻照區的中心位置。以附圖3所示參數以及光子晶體光纖一維熱傳導方程作為邊界條件，建立與二氧化碳激光器放電參數相關的光子晶體光纖三維溫度場分布模型。步驟3：光子晶體光纖與實心光纖熔接時導熱特性分析基于步驟2的數值仿真方法，要計算實心PCF與PM光纖熔接所需要的激光功率和放電時間，需要首先計算激光輻照區域的中心位置向實心PCF方向偏移的偏移量。偏移量的定義為：熔接時兩光纖端面中心位置為偏移量零點，向PM光纖方向移動，偏移量為正；向光子晶體光纖方向移動，偏移量為負。偏移量的值為激光輻照區中心位置至(x＝0，y＝0，z＝0)點的距離。由于二氧化碳用于光纖熔接時有兩個可控的熔接參數，即激光器功率P和放電時間t，同時，針對實心PCF與PM光纖熔接時的特殊性，還存在第三個熔接參數即激光輻照區中心的位置delta。這里需要計算出能使兩種光纖界面位置(即z＝0的位置)為整個被加熱區域的溫度最高點，二氧化碳激光器的加熱中心位置delta，以及兩光纖界面位置(即z＝0的位置)處的溫度曲線與激光器加熱功率P、加熱時間t的關系。對表1中不同時間下功率P，激光輻照區中心位置delta的取值進行仿真。表1仿真條件參數表可以得到確定加熱時間下，對應不同功率P與不同加熱中心z時，實心PCF與PM光纖上的溫度分布曲線。對確定時間下的仿真數值結果進行分析，溫度最高點的位置delta僅于加熱中心z的位置有關，與加熱功率無關，因此可以對加熱中心z和溫度最高點的位置delta進行二次項擬合，結果如式(5)所示。z＝-419.6delta2-0.945delta+7.943×10-5(7)可以求得溫度最高點的位置出現在兩光纖界面時，即z＝0時的加熱中心位置delta如表2所示。表2對應不同加熱時間加熱中心位置的數值結果序號二氧化碳激光器加熱時間T(ms)加熱中心位置delta(um)溫度最高點位置Z(um)1300113.680235090.220340088.420445086.50550081.10接下來通過對加熱功率P和溫度最高值T線性擬合，可以得到兩光纖界面位置(即z＝0的位置)處的溫度曲線與激光器加熱功率P、加熱時間t的關系模型。如附圖4所示為t＝300ms，對應不同的偏移量delta，不同加熱功率下，兩側光纖的溫度曲線分布。步驟4：光子晶體光纖與普通實心光纖熔接時力學特性分析光子晶體光纖受熱熔融后為石英液體，石英液體與空氣的交界面在微觀分子力的作用下，宏觀形成表面張力，表面張力使石英液體中的空氣孔收縮，收縮規律符合流體力學理論。由于空氣的粘度、密度都遠小于石英液體，因此，只研究石英液體這種不可壓縮流體在表面張力作用下的流場。同時，根據步驟3不同二氧化碳激光器放電參數下的兩側光纖溫度場分布模型，推導出石英光子晶體光纖熔融狀態下，溫度場分布與粘度系數模型，進而建立熔融狀態下光子晶體光纖流動方程，如式(8)(9)、(10)所示。▽·u＝0(10)其中，Fst為表面張力，U為流場速度，ρ為研究點處的密度，I為單位矩陣，t為時間，μ為粘度。式(9)、(10)來源于流體流動的Navier-Stokes方程。式(9)中，作用于氣液兩相交界面的表面張力與表面張力系數、曲率有關，由此建立式(10)的表面張力方程。Fst＝σκδn(11)式(11)中σ為表面張力系數，κ為曲率，δ為狄拉克函數(在氣液交界面處為1，在其他位置為0)，n為交界面的法線單位向量。式(7)中，粘度μ是端面溫度的函數，隨著端面溫度的提高，粘度數值變小。由步驟三可得，端面溫度是二氧化碳激光器加熱時間、加熱位置和加熱功率的函數。忽略石英液化時密度和液化潛熱引起的變化，可知光子晶體光纖端面空氣孔的收縮與二氧化碳激光器加熱時間、加熱位置和加熱功率有關。式(8)中不包含重力項，由于表面張力遠大于重力，故不考慮重力對光子晶體光纖收縮的影響。根據光子晶體光纖中氣液兩相界面的流動過程，使用氣液兩相流中的水平集方法對其石英-空氣界面進行追蹤，得到石英液體界面在表面張力下運動方程如式(11)所示。公式中，γ為重新初始化參數，ε為界面厚度參數，φ表示兩流體交界處的物質比例，ρ'為交界處的等效密度，μ'為交界處的等效粘度，ρ1為石英液體密度，ρ2為空氣氣體密度，μ1為石英液體粘度，μ2為空氣氣體粘度。根據φ的物理意義，定義φ＜0.5時為石英液體，φ＞0.5時為空氣流體。在忽略空氣密度和粘度的條件下，根據(9)式分析石英液體在表面張力作用下內部的流場速度分布，根據(12)式分析石英液體外界面的界面移動。結合式(9)和式(12)，依靠有限元分析手段，通過計算φ＝0.5的點的位置，即可追蹤石英液體界面在表面張力下運動的過程，進而建立不同二氧化碳激光器放電參數下光子晶體光纖空氣孔結構模型。附圖5所示為經過二氧化碳激光器的加熱，空氣孔發生塌陷后的表面結構示意圖。步驟5：建立二氧化碳激光器放電參數與熔接損耗的數值模型根據步驟1的模場損耗模型，以及實際應用中光子晶體光纖和普通實心光纖的結構參數計算滿足最低損耗要求，兩側光纖匹配的有效模場面積，進而求得受熱塌陷后光子晶體光纖的端面結構。將步驟3求得的不同放電時間下要達到兩側界面處(即z＝0)的位置為溫度最高點對應的加熱中心位置，以及不同放電時間t、放電功率P時，兩側光纖界面處(即z＝0)的位置溫度曲線作為步驟4的仿真條件，進而仿真計算出要得到最終模場匹配時光子晶體光纖的端面結構，需要的二氧化碳激光器的放電參數(放電時間t、放電中心位置delta，以及放電功率P)。實施例1本發明提出了一種通過控制光子晶體光纖空氣孔塌陷實現其與實心光纖低損耗熔接的方法。以下為具體實施例。在本實施例中，分以下四步進行計算：(1)根據步驟3的分析，高雙折射光子晶體光纖和熊貓保偏光纖熔接時，光纖軸向最高溫度位置與二氧化碳激光器加熱功率無關，與加熱時間、加熱位置有關。因此，可指定加熱時間和加熱位置，使其在兩種光纖交界面處溫度最高，接著可改變二氧化碳激光器加熱功率，求得適當的光子晶體光纖端面結構，使得熔接損耗最小。本算例選擇一個二氧化碳激光器加熱功率，在確定加熱時間，確定加熱位置下，計算熔接損耗。(2)在上述選定的二氧化碳激光器加熱功率、加熱時間、加熱位置下，計算兩種光纖軸向溫度分布。將兩種光纖交界處溫度與時間的關系以多項式函數擬合，得到溫度的時間函數：T＝T(t)(13)(3)在步驟4所述的力學模型中，將溫度T＝T(t)作為輸入，使粘度隨溫度變化，計算在粘度變化下的空氣孔收縮。收縮結束后，根據孔的收縮量及位置計算其有效模式。將有效模式下的電場強度輸出。(4)根據光子晶體光纖有效模式下的電場強度，以步驟1的理論，計算損耗。在開始計算之前，首先給出實心光子晶體光纖的結構尺寸如表3所示，計算過程中所需的物理參數如表4所示。表3實心PCF空氣孔結構尺寸表序號名稱長度(um)1光纖包層外徑802纖芯直徑(x)4.093纖芯直徑(y)8.184孔間距5.755大孔直徑7.216小孔直徑3.9表4物理參數表符號定義值單位CSiO2石英比熱容1345J.Kg-1.K-1Cair空氣比熱容1010J.Kg-1.K-1D光纖直徑80umR光纖半徑40umI二氧化碳激光器輻照度見式(1)W.m-2Ptotal激光器的輸出功率待定Wq熱流密度見式(8)W.m-3Qabs吸收系數3E-5無量綱t時間待定msT熔融溫度1700KWy，Wzy，z方向的激光束寬度1.5mmWabs能量吸收率/WSiO2石英密度2200Kg.m-3air空氣密度0.93Kg.m-3kSiO2石英熱傳導率2.68W.m-1.K-1Kair空氣熱傳導率0.032W.m-1.K-1根據附圖2，定義光纖軸向為z方向，光子晶體光纖z方向的范圍為0mm<z<3mm，熊貓光纖z方向的范圍為-3mm<z<0mm，二氧化碳激光器加熱的范圍為-1.5mm<z<1.5mm。選定加熱時間為500ms，選定加熱功率為1.7W。為求出在選定加熱時間下，使兩光纖交界處溫度最大的二氧化碳激光器加熱中心偏移量，選定二氧化碳激光器加熱中心位置在z軸負向的偏移為delta＝0:30um:300um。即從偏移量為0開始，每隔30um選擇一個偏移點進行計算，到偏移量為300um結束。根據每個偏移點的最高溫度位置函數擬合出最高溫度在兩光纖交界處的偏移量。偏移后的熱源范圍為-1.5mm-delta<z<1.5mm-delta，在以上邊界條件下，以有限元分析為手段，計算得到選定加熱時間為500ms，選定加熱功率為1.7W，各個偏移量下的最高溫度位置為如表5所示。表5各偏移量下的最高溫度及位置delta(um)位置(um)最大溫度(K)0811922.33130421917.44360271912.58390-61907.861120-361902.986150-721898.256180-1111893.655210-1381889.204240-1711885.176270-2071881.061300-2401877.102將最大值位置z和偏移量delta作多項式擬合，得：z＝-419.6delta2-0.945delta+7.943×10-5(14)令z＝0，求得偏移量為delta＝81.13um。即在加熱時間為500ms下，使得兩光纖交界面溫度最高的二氧化碳激光器中心偏移量為81.13um。觀察最大溫度，為1900K左右，在此溫度下石英液體的粘度極大，不利于光子晶體光纖空氣孔的收縮(將在后文具體闡述)。由于二氧化碳激光器中心偏移量與其加熱功率無關，所以提高加熱功率后，二氧化碳激光器中心偏移量仍為81.13um。將加熱功率以1.8W為起始，每隔0.1W取一點，至2.5W結束，求得在各個功率下的最大溫度如表6所示：表6不同加熱功率下的最大溫度功率(W)1.81.92.02.12.22.32.42.5最大溫度(K)20062101219722922388248325792675石英液體的沸點約為2600K，選擇加熱功率時，應保證此加熱功率下的最大溫度小于2600K。在模場直徑不匹配的情況下，應選擇一定的溫度使石英液體的粘度符合收縮要求，進而使空氣孔的收縮量一定，使其收縮后形成的模場符合使用要求。石英的粘度和溫度的關系如附圖6所示，粘度值隨溫度降低指數下降，空氣孔收縮速度也隨之加快。根據計算(由下文中空氣孔的收縮過程得到)，本發明中的光子晶體光纖在粘度數值為105(對應溫度2100K左右)時，收縮速度約為0.7um/s。在本例計算中，根據溫度與石英液體粘度的關系，選擇二氧化碳激光器加熱功率為2.2W。在二氧化碳激光器功率為2.2W下，0～0.5s時間內的溫度如附圖7所示。以二次多項式擬合圖8中的曲線，得到溫度與時間的關系為：由此可建立粘度與時間的關系，即μ＝μ(T(t))。根據步驟4的理論分析，計算在0～0.5s空氣孔的收縮情況。所得收縮量如圖8所示，從收縮量的數值可得，光子晶體光纖空氣孔收縮后的形狀近似為圓形，空氣孔排列的形式仍為三角形，全部空氣孔仍構成近似正六邊形。收縮之后的光子晶體光纖結構與原光子晶體光纖結構的比較如表7所示：表7光子晶體光纖收縮前后參數比較序號名稱收縮前(um)收縮后(um)1光纖包層外徑8076.622孔間距5.755.003大孔直徑7.215.184小孔直徑3.92.65根據上表進行光子晶體光纖端面的建模，以進行有效模式的計算。收縮前后模型的對比如圖9所示。在收縮后的模型下，根據步驟1的理論，可求得光在光子晶體光纖中的傳播模式如附圖10所示。同時，熊貓光纖的模式電場分布可以如下公式表示：其中，ω＝3.2um，去A＝1。，由公式(5)可計算得到耦合效率為η＝0.9493。故本算例中，光子晶體光纖與普通實心光纖的熔接損耗為：當前第1頁1 2 3