一種立銑刀磨削過程二維圖形仿真方法，用于仿真刀槽的二維截形，屬于二維仿真技術領域。

背景技術：

磨削加工仿真的主要目的是對磨削工藝的可行性及其磨削加工精度進行檢驗。但立銑刀的特征表面多由螺旋曲面、圓弧面等復雜曲線組成，難以對基于3D加工仿真得到的三維刀具模型進行測量，且三維仿真受實體布爾運算算法精度和圖形顯示效率的制約，3D仿真得到的刀具模型并不精確，對其的精度檢測并無實際意義。

目前，國內外大多刀具磨削軟件的功能主要側重于刀具的加工仿真，及與數控機床的聯機進行刀具的直接生產，主要利用三維模擬功能對加工過程中的碰撞、干涉進行監視，以調整砂輪姿態。然而，三維磨削仿真中通過砂輪包絡形成的刀具模型實質上是三維面片模型，難以在仿真得到的三維模型上找到法截面、端截面等設計基準，從而難以對仿真得到的三維模型進行精確測量。

通用的切削加工仿真軟件如VERICUT、MASTERCAM等提供了三維加工仿真功能，其也提供了三維測量功能，能對加工所得的三維模型進行距離、角度的測量，但其缺點也較顯著，缺點如下：

一、三維仿真得到的曲線擬合模型受圖形擬合精度的影響，其本身尺寸精度較底，測量數據有較大誤差，測量的意義不大；

二、針對立銑刀這類螺旋刀具，在仿真模型中難以得到其法剖面、端剖面，因此無法測量其法向前角、法后角、端面前角和端面后角等參數，從而難以對立銑刀具進行精確測量的問題。

技術實現要素：

本發明針對上述不足之處提供了一種立銑刀磨削過程二維圖形仿真方法，解決現有技術中三維仿真得到的曲線擬合模型受圖形擬合精度，因本身尺寸精度較底，測量數據有較大誤差；螺旋類立銑刀具，在仿真模型中難以得到法剖面、端剖面，因此無法測量立銑刀具法向前角、法后角、端面前角和端面后角等參數，從而難以對立銑刀具進行精確測量的問題。

為了實現上述目的，本發明采用的技術方案如下：

一種立銑刀磨削過程二維圖形仿真方法，其特征在于，如下步驟：

(1)首先讀取砂輪的刀位軌跡數據，獲取砂輪參數，并指定立銑刀具的剖切面位置， 得到立銑刀具的剖切面；

(2)分析砂輪與剖切面之間的相對位置關系，判斷刀位點對應的砂輪與剖切面是否相交，如果相交，轉到步驟(3)，反之，轉到步驟(1)；

(3)依次求解每一個刀位點對應的砂輪與剖切面的相交輪廓曲線，得到所有砂輪的剖切面輪廓，即得到砂輪截面曲線；

(4)將得到的所有砂輪剖切面輪廓疊加，得到立銑刀具刀槽的二維截形；

(5)最終對立銑刀具刀槽的二維截形進行測量，判斷仿真的刀槽的二維截形是否滿足加工精度，如果不滿足，則對磨削工藝進行修正。

進一步，所述步驟(1)中，具體步驟如下：

(11)首先砂輪的每個加工刀位的軌跡數據是由磨削工藝算法計算得到，即得到刀位點；

(12)采用通用的砂輪模型，通過磨削工藝算法計算得到工件坐標系O_w-X_wY_wZ_w中砂輪大端圓中心O_gmax的坐標值和砂輪軸矢量F_g的值，具體表示如下：

P_Ogmax＝{x_Ogmax，y_Ogmax，z_Ogmax}，

F_g＝[f_gx f_gy f_gz]^T，

其中，x_Ogmax、y_Ogmax、z_Ogmax和f_gx、f_gy、f_gz分別代表O_gmax的坐標值和F_g的矢量值在工件坐標系O_w-X_wY_wZ_w中的X、Y、Z方向的三個分量的值，T表示矩陣的轉置；

(13)在工件坐標系O_w-X_wY_wZ_w中，獲得剖切面M_c所在位置點P_c的坐標值為：

P_c＝{x_c，y_c，z_c}，

其中，x_c、y_c、z_c代表P_c的坐標值在工件坐標系O_w-X_wY_wZ_w中的X、Y、Z方向的三個分量的值；

(14)根據位置點P_c，給定剖切面M_c坐標系的三個矢量方向，分別為：

F_Xc、F_Yc、F_Zc分別表示剖切面坐標系的三個軸在工件坐標系下的矢量方向，其中，f_Xcx、f_Xcy、f_Xcz表示剖面坐標系的X軸在工件坐標系下矢量在X、Y、Z三個方向的矢量分量，f_Ycx、f_Ycy、f_Ycz表示剖面坐標系的Y軸在工件坐標系下矢量在X、Y、Z三個方向的矢量分量，f_Zcx、f_Zcy、f_Zcz表示剖面坐標系的Z軸在工件坐標系下矢量在X、Y、Z三個方向 的矢量分量；

(15)根據步驟(14)，得到剖切面法矢量F_c即為F_Zc，具體表示為：

F_c＝[f_cx f_cy f_cz]^T，

其中，f_cx、f_cy、f_cz代表F_c的法矢量在工件坐標系O_w-X_wY_wZ_w中的X、Y、Z三個方向的矢量分量；

(16)根據步驟(13)至步驟(15)可得，剖切面M_c的方程：

f_cx(x-x_c)+f_cy(y-y_c)+f_cz(z-z_c)＝0，

其中，x、y、z表示平面上的點的坐標值在X、Y、Z坐標方向上的分量，f_cx、f_cy、f_cz為剖切面M_c法矢量的三個分量。

進一步，所述步驟(2)的具體步驟如下：

(1)計算剖切面M_c與砂輪大端和小端邊線的交點P_c0、P_c1坐標值，其中，點P_c0、P_c1坐標值表達式分別為：

其中，和表示剖切面M_c所經過的點在砂輪坐標系O_g-X_gY_gZ_g下坐標值的X分量和Z分量，和表示剖切面M_c法矢量在砂輪坐標系O_g-X_gY_gZ_g下矢量值的X分量和Z分量；

(2)通過P_c0、P_c1兩點的X坐標值與判定條件進行比較，判定剖切面是否與砂輪相交及相交姿態，其中判定條件為：

|x_pc0|>R_gmax且|x_pc1|>R_gmin且x_pc0x_pc1>0，剖切面與砂輪不相交；

|x_pc0|>R_gmax且|x_pc1|>R_gmin且x_pc0x_pc1<0，剖切面與砂輪相交；

|x_pc0|≤R_gmax且|x_pc1|≤R_gmin，剖切面與砂輪相交；

|x_pc0|<R_gmax且|x_pc1|>R_gmin，剖切面與砂輪相交；

|x_pc0|>R_gmax且|x_pc1|<R_gmin，剖切面與砂輪相交；

其中，R_gmax和R_gmin分別為砂輪大端和小端的半徑。

進一步，所述步驟(3)的具體步驟如下：

(31)找到砂輪上與剖切面M_c垂直并過砂輪軸線的中心剖切面；

(32)定義砂輪坐標系O_g-X_gY_gZ_g，使得剖切面M_c與坐標平面X_gO_gZ_g垂直；

(33)根據砂輪坐標系、工件坐標系、砂輪坐標系到工件坐標的旋轉變換矩陣和平移變換式，得到砂輪坐標系與工件坐標系之間點坐標和矢量方向的變換關系；

(34)根據工件坐標系、剖切面坐標系、剖切面坐標系到工件坐標系的變換矩陣和工件坐標系到剖切面坐標系的變換矩陣，得到剖切面坐標系與工件坐標系之間點坐標和矢量方向的變換關系；

(35)根據砂輪坐標系、剖切面坐標系、砂輪坐標系到剖切面坐標系的變換矩陣，得到砂輪坐標系與剖切面坐標系之間的變換關系；

(36)根據步驟(33)至步驟(35)的坐標變換、得到在砂輪坐標系下剖切面所經過的點坐標和法矢量方向，得到求解每一個刀位點對應的砂輪與剖切面的相交輪廓曲線，以及所有砂輪的剖切面輪廓。

進一步，所述步驟(31)中，具體如下：

指定的剖切面與砂輪軸矢量不垂直，砂輪的中心剖切面M_p過砂輪軸線且與剖切面M_c相垂直，則法矢量F_p可F_p＝F_g×F_c，具體如下：

f_px、f_py、f_pz分別為砂輪的中心剖切面M_p的法矢量的三個分量，式中的f_gx、f_gy、f_gz為砂輪軸矢量的三個分量，f_cx、f_cy、f_cz為剖切面M_c法矢量的三個分量；

得到砂輪的中心剖切面M_p的方程為：

f_px(x-x_Ogmax)+f_py(y-y_Ogmax)+f_pz(z-z_Ogmax)＝0。

進一步，所述步驟(32)中，定義砂輪坐標系O_g-X_gY_gZ_g的具體步驟如下：

(321)將坐標原點定在砂輪大端圓圓心點O_gmax；

(322)Z_g軸方向為砂輪軸矢量方向，即F_Zg＝F_g；

(323)Y_g軸方向為平面M_p的法矢量方向，即F_Yg＝F_p；

(324)X_g軸位于砂輪的中心剖切面M_p內，即F_Xg＝F_Yg×F_Zg；

進一步，所述步驟(33)中，具體步驟如下：

(331)設P_g＝[P_gxP_gyP_gz]^T、P_w＝[P_wxP_wyP_wz]^T分別為砂輪坐標系和工件坐標系下的點坐標；

(332)設N_g＝[N_gxN_gyN_gz]^T、N_w＝[N_wxN_wyN_wz]^T分別為砂輪坐標系和工件坐標系下的矢量值；

(333)根據步驟(331)至步驟(332)，得到砂輪坐標系O_g-X_gY_gZ_g中的點坐標和矢量方向到工件坐標系O_w-X_wY_wZ_w中的點坐標和矢量方向的變換關系：

P_w＝T_g-w+M_g-wP_g，

N_w＝M_g-wN_g，

T_g-w＝[x_Ogmax y_Ogmax z_Ogmax]^T，

式中，M_g-w為砂輪坐標系到工件坐標系的旋轉變換矩陣，T_g-w為砂輪坐標系到工件坐標系平移變換式；

(334)根據步驟(331)至步驟(332)，得到工件坐標系O_w-X_wY_wZ_w中的點坐標和矢量方向到砂輪坐標系O_g-X_gY_gZ_g中的點坐標和矢量方向的變換關系：

P_g＝M_w-g(P_w+T_w-g)；

N_g＝M_w-gN_w；

T_w-g＝[-x_Ogmax -y_Ogmax -z_Ogmax]^T。

式中，M_w-g為工件坐標系到砂輪坐標系的旋轉變換矩陣，T_w-g為工件坐標系到砂輪坐標系平移變換式。

進一步，所述步驟(34)中，具體步驟如下：

(341)剖切面坐標系到工件坐標系的變換矩陣為：

(342)工件坐標系到剖切面坐標系的變換矩陣為：

式中，

(343)設P_c＝[P_cxP_cyP_cz]^T為剖切面坐標系下的點坐標；N_c＝[N_cxN_cyN_cz]^T為剖切面坐標系下的矢量值，則工件坐標系O_w-X_wY_wZ_w中的點坐標和矢量方向到剖切面坐標系O_c-X_cY_cZ_c中的點坐標和矢量方向的變換關系為：

P_c＝M_w-c(P_w+T_w-c)，

N_c＝M_c-wN_w，

T_w-c＝[-P_cx-P_cy-P_cz]^T。

進一步，所述步驟(35)中，具體如下：

砂輪坐標系到剖切面坐標系的變換矩陣為：

式中，

則砂輪坐標系O_g-X_gY_gZ_g中的點坐標和矢量方向到剖切面坐標系O_c-X_cY_cZ_c中的點坐標和矢量方向的變換關系為:

P_c＝M_g-c(P_g+T_g-c)，

N_c＝M_g-cN_g，

則T_g-c＝[x_Ogmax-P_cxy_Ogmax-P_cyz_Ogmax-P_cz]^T。

進一步，所述步驟(36)中，具體步驟如下：

(361)根據坐標變換即可得到在砂輪坐標系O_g-X_gY_gZ_g下剖切面M_c所經過的點坐標為：

(362)根據坐標變換即可得到在砂輪坐標系O_g-X_gY_gZ_g下剖切面M_c的法矢量方向為：

(363)根據步驟(361)至步驟(362)在砂輪的中心剖切面M_p在砂輪坐標系O_g-X_gY_gZ_g中的方程為：

(364)在砂輪坐標系O_g-X_gY_gZ_g下，在任意位置z處砂輪回轉半徑為：

R_z＝R_gmax-ztanκ_g，

則砂輪輪廓曲面方程為：x²+y²＝(R_gmax-ztanκ_g)²；

(365)砂輪為回轉體，剖切面與砂輪相交所得的截形曲線相對坐標平面X_gO_gZ_g呈對稱分布，在得到剖切面與砂輪的相交范圍H_c0≤z≤H_c1之后，H_c0和H_c1分別為砂輪坐標系中相交范圍內的點z坐標的最小、最大值，在相交范圍內的任意位置z＝H_c處，得到截形曲線上對稱兩點P_c0、P_c1的坐標值，由此得到對稱分布的兩條截形曲線方程為：

綜上所述，由于采用了上述技術方案，本發明的有益效果是：

一、本發明中二維仿真能將復雜的三維形體以二維圖形的方式呈現，更便于對加工精度的測量，以便于在加工結果不滿足精度要求時，快速修正加工工藝；

二、通過建立特殊位置的砂輪坐標系O_g-X_gY_gZ_g，將空間中的曲面與平面的三維位置關系轉化為砂輪坐標系下的砂輪二維輪廓線與剖切面M_c之間的位置關系，以降低求交計算難 度；

三、建立特殊的砂輪坐標系O_g-X_gY_gZ_g，使得剖切面M_c與坐標平面X_gO_gZ_g垂直；

四、利用刀具磨削過程中砂輪與刀體之間的運動關系，在刀具剖切面位置處的砂輪二維截面進行輪廓計算，通過砂輪包絡運動中多個砂輪截面輪廓在刀具剖切面位置處的動態疊加，得到刀具任意二維剖切面的磨削形狀，實現了刀具前角、后角、槽深等結構參數磨削精度的驗證，解決了刀具設計缺陷在設計期間難以得到加工驗證問題。

附圖說明

圖1為本發明中工件坐標系中砂輪與剖切面的結構示意圖；

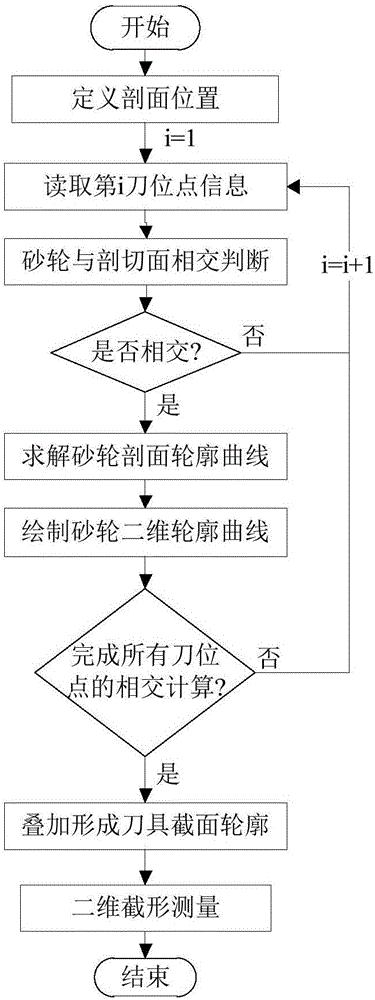
圖2為本發明中刀槽的二維截形的流程示意圖；

圖3為本發明中砂輪結構示意圖；

圖4為本發明中砂輪與剖切面的位置關系結構示意圖；

圖5為本發明中在砂輪坐標系下的砂輪曲面輪廓結構示意圖；

圖6為本發明中砂輪截形曲線計算的結構示意圖；

圖7為本發明中立銑刀二維加工仿真結構示意圖；

圖8為本發明中砂輪與剖切面相交判斷的5種相交形式，a為不相交、b為相交狀態1、c為相交狀態2、d為相交狀態3、e為相交狀態4；

圖中標記：1-剖切面、2-砂輪、3-中心剖切面、4-砂輪截面曲線、5-立銑刀具截面曲線。

具體實施方式

為了使本發明的目的、技術方案及優點更加清楚明白，以下結合附圖及實施例，對本發明進行進一步詳細說明。應當理解，此處所描述的具體實施例僅用以解釋本發明，并不用于限定本發明。

磨削加工仿真的主要目的是對磨削工藝的可行性及其磨削加工精度進行檢驗。但立銑刀的特征表面多由螺旋曲面、圓弧面等復雜曲線組成，難以對基于3D加工仿真得到的三維刀具模型進行測量，且三維仿真受實體布爾運算算法精度和圖形顯示效率的制約，3D仿真得到的刀具模型并不精確，對3D仿真得到的刀具模型的精度檢測并無實際意義。而二維仿真能將復雜的三維形體以二維圖形的方式呈現，更便于對加工精度的測量，以便于在加工結果不滿足精度要求時，快速修正加工工藝。

本發明通過將砂輪沿其軸線方向呈片狀離散成多個平面并與給定的剖切面求交得到離散的砂輪包絡體剖切面曲線，將三維求交問題簡化；并將離散的砂輪包絡體剖切面輪廓曲線(即砂輪截面曲線)疊加得到完整的立銑刀具剖切輪廓曲線。

二維截形仿真的實現原理：

如圖1所示，基于砂輪刀軌的二維截形仿真即是假設工件(立銑刀具)不動，研究刀具(砂輪)在工件固定坐標系O_w-X_wY_wZ_w中作加工運動時砂輪與立銑刀具剖切面M_c之間的位置關系，進行兩者之間的求交計算得到多個砂輪在剖切面處的截形疊加，形成剖切面處的刀槽二維廓形。

二維截形仿真的具體實現流程可歸結為：首先讀取砂輪的刀位軌跡數據，獲取砂輪參數，并指定立銑刀具的剖切面M_c位置；分析砂輪與剖切面之間的相對位置關系，并依次求解每一個刀位點對應的砂輪與指定剖切面M_c的相交輪廓曲線；將所得砂輪的剖切面輪廓(即砂輪截面曲線)疊加即得到完整的立銑刀具刀槽截形(刀槽的二維截形)，最終對仿真得到的刀槽的二維截形進行測量以判斷加工精度是否滿足要求。具體實現流程如圖2所示。

刀槽的二維截形的關鍵點是進行砂輪與剖切面M_c兩者之間的求交得到砂輪截面曲線。而在砂輪坐標系中，砂輪與剖切面兩者分別為圖1所示的三維曲面與空間平面，若直接進行兩者之間的求交計算，難以確定兩者之間的相對位置關系，計算過程復雜。本發明利用砂輪的回轉體特性，通過建立特殊位置的砂輪坐標系O_g-X_gY_gZ_g，將空間中的曲面與平面的三維位置關系轉化為砂輪坐標系下的砂輪二維輪廓線與剖切面M_c之間的位置關系，以降低求交計算難度。

判定剖切面是否與砂輪相交及相交姿態：

首先計算指剖切面M_c與砂輪大端和小端邊線的交點P_c0、P_c1坐標值，其中點P_c0、P_c1坐標值表達式分別為：

通過P_c0、P_c1兩點的X坐標值與判定條件進行比較，判定剖切面是否與砂輪相交及相交姿態，其中判定條件為如圖8和下述表1所示：

相交狀態判定表：

表1

工件坐標系中砂輪與剖切面位置的定義：

如圖1所示為工件坐標系O_w-X_wY_wZ_w中的砂輪和剖切面M_c。砂輪的每個加工刀位的軌跡是由磨削工藝算法計算得到的，并可得到砂輪大端圓中心O_gmax的坐標值和砂輪軸矢量F_g的值，分別表示為：

P_Ogmax＝{x_Ogmax，y_Ogmax，z_Ogmax}；

F_g＝[f_gx f_gy f_gz]^T；

此外，常用砂輪形狀有盤形、碟形、碗形等，本發明統一采用砂輪通用幾何模型進行描述，主要參數包括大端半徑R_gmax、厚度H_g、錐角κ_g。

在二維截形仿真中，剖切面M_c是由人為指定的需要查看的立銑刀具截面曲線。在立銑刀具的設計中，立銑刀具主要設計參數均基于端截面、法截面等典型截面定義，故加工得到的端截面、法截面上的刀槽截形是關注的重點，而為使仿真方法具有通用性，本發明使剖切面可位于空間中任意位置，并統一定義為剖切面M_c。

設在工件坐標系O_w-X_wY_wZ_w中剖切面M_c所在位置點P_c的坐標值為：

P_c＝{x_c，y_c，z_c}；

給定剖切面坐標系的三個矢量方向分別為：

剖切面法矢量F_c即為F_Zc，表示為：

F_c＝[f_cx f_cy f_cz]^T；

則剖切面M_c的方程可寫為：

f_cx(x-x_c)+f_cy(y-y_c)+f_cz(z-z_c)＝0；

砂輪坐標系的定義及其與工件坐標系之間的位置關系：

確定了工件坐標系O_w-X_wY_wZ_w下的砂輪位置及剖切面位置，而更為重要的是要確定砂輪 與剖切面之間的位置關系，且最終得到剖切面與砂輪輪廓曲面的相交曲線。但是已經給定的砂輪大端圓中心O_gmax的坐標值及軸矢量F_g僅僅是確定了砂輪的位置及姿態，尚不能直接建立砂輪輪廓曲面方程。故需要建立一個特殊的砂輪坐標系O_g-X_gY_gZ_g以便于確定其與工件坐標系O_w-X_wY_wZ_w之間的相對位置關系。

①砂輪坐標系的定義

根據解析幾何原理，由于砂輪為回轉體，當剖切面與砂輪軸矢量不垂直時，在空間中總可以找到砂輪的一個中心剖切面M_p，中心剖切面過砂輪中心軸線且與剖切面M_c垂直。砂輪與剖切面的位置關系可表示為如圖4所示。

由于砂輪中心面M_p過砂輪軸線且與剖切面M_c垂直，則中心剖切面法矢量F_p可由F_p＝F_g×F_c求得：

砂輪中心剖切面M_p的方程為：

f_px(x-x_Ogmax)+f_py(y-y_Ogmax)+f_pz(z-z_Ogmax)＝0；

確定砂輪中心剖切面M_p后，則按如下規則建立砂輪坐標系O_g-X_gY_gZ_g：其坐標原點位于砂輪大端圓圓心點O_gmax處，Z_g軸方向為砂輪軸矢量方向，Y_g軸方向為平面M_p的法矢量方向，X_g軸則根據右手定則確定，實際上X_g軸位于砂輪中心面M_p內。

則在工件坐標系O_w-X_wY_wZ_w中，砂輪坐標系O_g-X_gY_gZ_g的坐標軸Z_g矢量方向F_Zg＝F_g，即為：

砂輪坐標系O_g-X_gY_gZ_g的坐標軸Y_g矢量方向F_Yg＝F_p，即為：

砂輪坐標系O_g-X_gY_gZ_g的坐標軸X_g矢量方向則根據F_Xg＝F_Yg×F_Zg求得：

建立特殊的砂輪坐標系O_g-X_gY_gZ_g的優點在于，使得剖切面M_c與坐標平面X_gO_gZ_g垂直。

②砂輪坐標系與工件坐標系之間的變換關系

因為式f_cx(x-x_c)+f_cy(y-y_c)+f_cz(z-z_c)＝0是基于工件坐標系所定義的剖切面方程，若要得到砂輪坐標系O_g-X_gY_gZ_g下的剖切面方程，則需先確定砂輪坐標系與工件坐標系之間的關系。

設P_g＝[P_gxP_gyP_gz]^T、P_w＝[P_wxP_wyP_wz]^T分別為砂輪坐標系和工件坐標系下的點坐標；N_g＝[N_gxN_gyN_gz]^T、N_w＝[N_wxN_wyN_wz]^T分別為砂輪坐標系和工件坐標系下的矢量值，則砂輪坐標系O_g-X_gY_gZ_g中的點坐標和矢量方向到工件坐標系O_w-X_wY_wZ_w中的點坐標和矢量方向的變換關系為：

P_w＝T_g-w+M_g-wP_g；

N_w＝M_g-wN_g；

式中，M_g-w為砂輪坐標系到工件坐標系的旋轉變換矩陣，T_g-w砂輪坐標系到工件坐標系平移變換式，其表達式分別為：

T_g-w＝[x_Ogmax y_Ogmax z_Ogmax]^T；

首先設

上述中已經得到了砂輪坐標系的三個軸的方向矢量值在工件坐標系下的值，即F_Xg、F_Yg、F_Zg，而在砂輪坐標系下，其三個軸的方向矢量值分別為：

根據轉換公式有：

于是可求得矩陣M_g-w中的各元素值；

設T_w-g＝[t_wgx t_wgy t_wgz]^T，上述中已經給出了砂輪坐標原點在工件坐標系中的位置值，即

P_Ogmax＝{x_Ogmax，y_Ogmax，z_Ogmax}；

而在砂輪坐標系中，其原點坐標值為

根據變換關系：

即可求解得到T_g-w中各元素值。

而工件坐標系O_w-X_wY_wZ_w的點坐標和矢量方向到砂輪坐標系O_g-X_gY_gZ_g中的點坐標和矢量方向的變換關系分別表示為：

P_g＝M_w-g(P_w+T_w-g)；

N_g＝M_w-gN_w；

式中，

T_w-g＝[-x_Ogmax -y_Ogmax -z_Ogmax]^T；

根據M_g-w求逆得到M_w-g；根據T_g-w求逆得到T_w-g。

③剖切面坐標系與工件坐標系之間的變換關系

剖切面坐標系到工件坐標系的變換矩陣為：

工件坐標系到剖切面坐標系的變換矩陣為：

首先設

上述已經給出了剖切面坐標系的三個軸的方向矢量在工件坐標系中的值，即：

而剖切面坐標系中，其三個軸的方向矢量分別為：

根據轉換方程：

即求解得到M_c-w和各元素值，由M_c-w求逆得到M_w-c。

式中，

設P_c＝[P_cxP_cyP_cz]^T為剖切面坐標系下的點坐標；N_c＝[N_cxN_cyN_cz]^T為剖切面坐標系下的矢量值，則工件坐標系O_w-X_wY_wZ_w中的點坐標和矢量方向到剖切面坐標系O_c-X_cY_cZ_c中的點坐標和矢量方向的變換關系為：

P_c＝M_w-c(P_w+T_w-c)；

N_c＝M_c-wN_w；

式中，T_w-c＝[-P_cx-P_cy-P_cz]^T。

④砂輪坐標系與剖切面坐標系之間的變換關系

砂輪坐標系到剖切面坐標系的變換矩陣為：

則砂輪坐標系O_g-X_gY_gZ_g中的點坐標和矢量方向到剖切面坐標系O_c-X_cY_cZ_c中的點坐標和矢量方向的變換關系為：

P_c＝M_g-c(P_g+T_g-c)；

N_c＝M_g-cN_g；

式中，T_g-c＝[x_Ogmax-P_cxy_Ogmax-P_cyz_Ogmax-P_cz]^T。

(4)砂輪與剖切面求交計算

根據坐標變換即可得到在砂輪坐標系O_g-X_gY_gZ_g下剖切面M_c所經過的點坐標為：

在砂輪坐標系O_g-X_gY_gZ_g下剖切面M_c的法矢量方向為：

則剖切面M_p在砂輪坐標系O_g-X_gY_gZ_g中的方程為：

如圖5所示，在砂輪坐標系O_g-X_gY_gZ_g下在任意位置z處砂輪回轉半徑為：

R_z＝R_gmax-ztanκ_g；

則砂輪輪廓曲面方程為：

x²+y²＝(R_gmax-ztanκ_g)²；

由于砂輪為回轉體，剖切面與砂輪相交所得的截形曲線相對坐標平面X_gO_gZ_g呈對稱分布，在得到剖切面與砂輪的相交范圍(H_c0≤z≤H_c1)之后，在相交范圍內的任意位置z＝H_c處，根據砂輪坐標系O_g-X_gY_gZ_g中的點坐標和矢量方向到剖切面坐標系O_c-X_cY_cZ_c中的點坐標和矢量方向的變換關系和砂輪坐標系O_g-X_gY_gZ_g下剖切面M_c所經過的點坐標即可得到截形曲線上對稱兩點P_c0、P_c1的坐標值。

而對稱分布的兩條截形曲線方程為：

得到砂輪坐標系下的砂輪截形曲線之后，通過砂輪坐標系O_g-X_gY_gZ_g中的點坐標和矢量方向到工件坐標系O_w-X_wY_wZ_w中的點坐標和矢量方向的變換關系、砂輪坐標系O_g-X_gY_gZ_g中的點坐標和矢量方向到剖切面坐標系O_c-X_cY_cZ_c中的點坐標和矢量方向的變換關系即可得到工件坐標系或剖切面坐標系下的砂輪截形曲線，最終所有經過剖切面的多個砂輪截形疊加即可得到立銑刀具截面曲線。

本發明提出基于砂輪截形動態投影的加工仿真方法，利用刀具磨削過程中砂輪與刀體之間的運動關系，在立銑刀具剖切面位置處的砂輪二維截面進行輪廓計算，通過砂輪包絡運動中多個砂輪截面輪廓在立銑刀具剖切面位置處的動態疊加，得到刀具任意二維剖切面的磨削形狀，實現了刀具前角、后角、槽深等結構參數磨削精度的驗證，解決了刀具設計缺陷在設計期間難以得到加工驗證問題。

以上所述僅為本發明的較佳實施例而已，并不用以限制本發明，凡在本發明的精神和原則之內所作的任何修改、等同替換和改進等，均應包含在本發明的保護范圍之內。