本發明涉及一種油氣田開發領域，特別是關于一種基于蒙特卡洛算法的聚合物驅生產優化方法和系統。

背景技術：

國內外油田經過多年水驅開發，已進入高含水階段，水驅驅油效率明顯下降，嚴重影響了開發效果。因此，為了對老油田進行再次開發，三次采油逐步推廣，其中聚合物驅是最為重要的一種改善波及效率進而提高開發效果的三次采油技術。盡管聚合物驅成本較高，但因其能夠實現明顯降水增油或者控水增油的效果，也廣被工程師們所接受。正是由于該技術具有成本較高的缺點，因此，需要通過油藏開發實時生產優化技術，節約成本，改善聚合物驅開發，最大化開發收益和效果。

油藏開發生產實時優化是近年來新興的一種開發方案預測方法，其目前主要應用于水驅開發油藏，與聚合物驅應用結合研究目前較少。該方法與聚合物驅結合是基于對當前油藏地質和生產條件的認識，并從油藏長期開發效益出發，利用油藏數值模擬和最優控制理論自動優化計算油水井不同階段的注采參數(如注入聚合物濃度、注入聚合物時機、井底流壓、油水井流量等)，確定最優的生產開發方案，使油藏開發盡可能處于最佳狀態，從而節約聚合物驅生產成本，改善開發效果。油藏生產優化屬于大系統最優化控制問題，涉及到的變量多，維數高，實現求解十分困難。目前主要使用的伴隨梯度方法進行優化計算，該方法需要了解油藏模擬器代碼層面實現，通過編寫伴隨矩陣嵌入油藏數值模擬計算來獲取伴隨梯度，求解過程異常復雜，僅限于一些概念油藏模型進行理論研究與應用，難以推廣應用于成熟的商業模擬器。因此，無梯度類方法成為生產優化算法的熱點，enopt算法、newuoa算法、qim-ag算法等被應用水驅生產優化，還未涉及聚合物驅生產優化。現有技術中利用隨機擾動逼近算法(spsa)結合有限差分算法(fdsa)對聚合物用量進行了優化實現了優化后的調控方案在使用了同樣的聚合物用量的情況下，降水增油效果更加明顯，改善了聚合物驅的效果。但作為隨機擾動類逼近算法所生成的生產調控方案在時間上變化十分劇烈不夠平滑，難以在現場實際應用。

技術實現要素：

針對上述問題，本發明的目的是提供一種基于蒙特卡洛算法的聚合物驅生產優化方法和系統，其容易實現，而且優化效率高，收斂速度快，易于和任意油藏數值模擬器相結合進行聚合物驅生產優化的計算，能夠同時優化注采井生產參數和注入聚合物濃度。

為實現上述目的，本發明采取以下技術方案：一種基于蒙特卡洛算法的聚合物驅生產優化方法，其特征在于包括以下步驟：1)根據油藏數值模擬器生成油藏優化的最優控制函數；2)由球形模型生成協方差矩陣，利用蒙特卡洛逼近算法在最優控制變量附近生成初始擾動向量，并采用協方差矩陣對初始擾動向量進行處理，生成目標擾動向量；3)采用包括目標擾動向量的蒙特卡洛算法對最優控制函數進行求解，生成最優開發效益對應的最優注采參數。

進一步，所述步驟1)中，以開發期內經濟凈現值npv來評價聚合物驅開發效益，得到最優控制函數：

第一約束條件為：ei(u)＝0,i∈ii，

第二約束條件為：ej(u)≤0,j∈ij，

第三約束條件為：u^low≤u≤u^up；

其中，j(u)表示聚合物驅的開發效益,u為注采參數對應的控制向量；l為控制時間；np為生產井數；ni為注水井數，npi為注聚井數；分別為產油、產水、注水速度及注聚量；ro、rw、rwi、rp、b分別表示原油價格、產水成本、注水成本、聚合物價格和年利率,δtⁿ為n時刻模擬計算時間步，tⁿ為n時刻累積計算時間；ei(u)表示等式約束方程；ii表示等式約束個數；ej(u)表示不等式約束方程；ij表示不等式約束個數；u^low表示控制變量下邊界值；u^up表示控制變量上邊界值。

進一步，所述步驟2)中，采用協方差矩陣對所述初始擾動向量進行光滑處理和搜索方向篩選，生成目標擾動向量。

進一步，所述步驟3)中，對最優控制函數進行求解具體過程如下：3.1)生成優化參數以及迭代步l等于0對應的第一控制變量u^l；3.2)采用對數變換方法將第一控制變量u^l轉換為第三約束條件對應的無約束優化條件下的第二控制變量s^l；3.3)將第二控制變量s^l帶入到最優控制函數中，生成對應的第一函數值j(s^l)；3.4)利用包括目標擾動向量和優化參數的蒙特卡洛算法求取最優控制函數在第二控制變量s^l處的蒙特卡洛梯度；3.5)根據投影梯度優化方法，采用優化參數和步驟3.4)計算出的蒙特卡洛梯度，將第二控制變量s^l轉換為滿足第一約束條件和第二約束條件的第三控制變量s^l+1；3.6)計算第三控制變量s^l+1對應的第二函數值，并比較第二函數值和第一函數值，若第二函數值大于第一函數值，則將第三控制變量s^l+1設定為目標控制變量；否則，將迭代步長減半，并返回至步驟3.5)；3.7)判斷第二函數值是否滿足預設的收斂條件，若滿足，則輸出第二函數值為最優開發效益,輸出目標控制變量為最優注采參數對應的控制向量；若不滿足，則令迭代步加1，并返回至步驟3.2)；或者判斷迭代次數是否達到預設的最大迭代次數，若是，則輸出第二函數值為最優開發效益,輸出目標控制變量為最優注采參數對應的控制向量，若否，則令迭代步加1，并返回至步驟3.2)。

進一步，所述步驟3.2)中，采用第一公式將第一控制變量u^l轉換為第三約束條件對應的無約束優化條件下的第二控制變量s^l，第一公式為：

其中，表示變換后的第i個控制變量；表示變量u在第l^th迭代步下的第i^th個控制分量，表示上界，表示下界。

進一步，所述步驟3.4)中，蒙特卡洛梯度求解過程為：3.4.1)在第l個迭代步，生成了nr個用于計算近似梯度的目標函數值設δj^j為第j個擾動向量s^l,j生成的目標函數值與當前最優控制變量s^l所對應的目標函數值之差；3.4.2)在第l個迭代步，令第j個擾動向量的第i個元素為則蒙特卡洛梯度為：

進一步，所述步驟3.5)中，采用第二公式將第二控制變量s^l轉換為滿足第一約束條件和第二約束條件的第三控制變量s^l+1。

進一步，所述第二公式包括無需歸位移動時對應的第二公式：以及需要歸位移動時對應的第二公式：

一種基于蒙特卡洛算法的聚合物驅生產優化系統，其特征在于：該系統包括模型建立模塊、擾動向量生成模塊和優化模塊；所述模型建立模塊用于根據油藏數值模擬器生成油藏優化的最優控制函數；所述擾動向量生成模塊用于生成協方差矩陣和初始擾動向量，并采用協方差矩陣對初始擾動向量進行處理，生成目標擾動向量；所述優化模塊用于采用包括目標擾動向量的蒙特卡洛算法對最優控制函數進行求解，生成最優開發效益對應的最優注采參數。

進一步，所述優化模塊包括第一生成單元、第一變換單元、第一計算單元、第二計算單元、第二變換單元、比較單元和收斂判斷單元；所述第一生成單元，用于生成優化參數以及迭代步l等于0對應的第一控制變量u^l，優化參數包括迭代步長和擾動常數；所述第一變換單元，用于采用對數變換方法將第一控制變量u^l轉換為第一約束條件對應的無約束優化條件下的第二控制變量s^l；所述第一計算單元，用于將第二控制變量s^l帶入到最優控制函數中，生成對應的第一函數值；所述第二計算單元，用于利用包括目標擾動向量和優化參數的蒙特卡洛算法求取最優控制函數在第二控制變量s^l處的蒙特卡洛梯度；所述第二變換單元，用于根據投影梯度優化方法，采用優化參數和所述蒙特卡洛梯度，將第二控制變量s^l轉換為滿足第二約束條件和第三約束條件的第三控制變量s^l+1；所述比較單元，用于將第三控制變量s^l+1帶入到最優控制函數中，生成對應的第二函數值；并比較第二函數值和第一函數值，若第二函數值大于第一函數值，則將第三控制變量s^l+1設定為目標控制變量，否則，將迭代步長減半，并驅動第二變換單元生成新的第三控制變量s^l+1；所述收斂判斷單元，用于判斷第二函數值是否滿足預設的收斂條件，若是，則輸出第二函數值為最優開發效益，輸出目標控制變量為最優注采參數對應的控制向量，若否，則令迭代步加1，并驅動第一變換單元；或者收斂單元用于判斷迭代次數是否達到預設的最大迭代次數，若是，則輸出第二函數值為最優開發效益，輸出目標控制變量為最優注采參數對應的控制向量，若否，則令迭代步加1，并驅動第一變換單元開始下一次迭代過程。

本發明由于采取以上技術方案，其具有以下優點：1、本發明對現有的油藏開發方法進行了優化，不僅計算過程簡單，容易實現，而且優化效率高，收斂速度快，易于和任意油藏數值模擬器相結合進行聚合物驅生產優化的計算，能夠同時優化注采井生產參數和注入聚合物濃度，并且本發明的生產優化調控方案考慮了在時間上的相關性，更為平滑易于現場實施并能顯著改善油藏開發效果，為科學合理的進行油田高效開發提供了重要的決策依據。2、由于不同的最優控制函數可以得到不同的優化結果，針對油田開發的實際情況，本發明以開發期內經濟凈現值(npv)來評價聚合物驅開發效益，同時采用了新的最優控制函數，可以同時對注采量、注聚量和段塞大小進行優化，具有較高的優化效率且優化結果準確直觀。3、本發明引入協方差矩陣對現有的蒙特卡洛算法進行改進，具有使梯度光滑、對梯度方向進行篩選的作用，進而使得近似梯度與真實梯度夾角更小、更接近于真實梯度，從而達到加快收斂速度、提高算法的收斂速度的目的。4、本發明將相應的約束優化問題轉換為無約束優化問題，簡化了優化過程，提高了優化速度和效率。同時，采用投影梯度優化方法，即采用投影移動和歸位移動兩個過程，使得到的第三控制變量滿足預設的優化條件，提高了優化結果的準確性。本發明可以廣泛在油氣田開發領域中應用。

附圖說明

圖1是本發明基于蒙特卡洛算法的聚合物驅生產優化方法的流程示意圖；

圖2a是本發明實施例中采用現有技術聚合物驅生產優化方法的歸一化梯度圖；

圖2b是本發明實施例中采用聚合物驅生產優化方法優化后的歸一化梯度圖；

圖3是本發明實施例中采用聚合物驅生產優化方法優化后的滲透率場分布圖；

圖4是本發明實施例中采用本發明方法和采用現有技術聚合物驅生產優化方法的凈現值優化結果對比圖；

圖5是本發明實施例中采用聚合物驅生產優化方法和采用現有技術聚合物驅生產優化方法的區塊含水率優化結果對比圖；

圖6a是本發明實施例中優化前飽和度場圖；

圖6b是本發明實施例中采用現有技術聚合物驅生產優化方法的飽和度場圖；

圖6c是本發明實施例中采用聚合物驅生產優化方法優化后的飽和度場圖；

圖7是本發明實施例中采用聚合物驅生產優化方法和采用現有技術聚合物驅生產優化方法的聚合物濃度優化結果對比圖；

圖8是本發明實施例中采用聚合物驅生產優化方法和采用現有技術聚合物驅生產優化方法的聚合物段塞優化結果對比圖；

圖9是本發明實施例中采用聚合物驅生產優化方法和采用現有技術聚合物驅生產優化方法的注水量優化結果對比圖；

圖10a是本發明實施例中采用現有技術聚合物驅生產優化方法的產液量優化結果圖；

圖10b是本發明實施例中采用聚合物驅生產優化方法優化后的產液量優化結果圖；

圖11是本發明基于蒙特卡洛算法的聚合物驅生產優化系統的結構示意圖。

具體實施方式

本發明的基本思想是首先把對油藏生產體系的控制描述成一個最優化問題，借助油藏數值模擬技術建立了油藏生產最優控制模型；在考慮油藏實際注采參數特點的基礎上，通過引入控制參數協方差矩陣，并采用蒙特卡洛梯度逼近算法對所建控制模型進行求解，獲得最優油藏注采參數及注入聚合物濃度。所得最優調控方案考慮了油水井注采參數間的相關性，便于實際操作并能顯著改善油藏開發效果，為科學合理的進行油田高效開發提供了重要的決策依據。下面結合附圖和實施例對本發明進行詳細的描述。

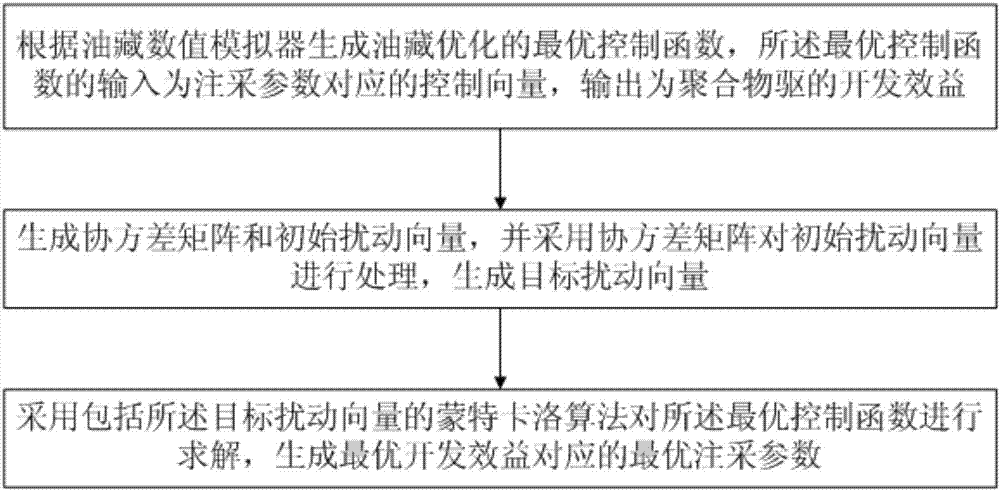
如圖1所示，本發明提供一種基于蒙特卡洛算法的聚合物驅生產優化方法，其包括以下步驟：

1)根據油藏數值模擬器生成油藏優化的最優控制函數；最優控制函數的輸入為注采參數對應的控制向量，輸出為聚合物驅的開發效益；

2)由球形模型生成協方差矩陣，利用蒙特卡洛逼近算法在最優控制變量附近生成初始擾動向量，并采用協方差矩陣對初始擾動向量進行處理，生成目標擾動向量；

3)采用包括目標擾動向量的蒙特卡洛算法對最優控制函數進行求解，生成最優開發效益對應的最優注采參數。

可選地，作為本發明的一個實施例，步驟1)中基于油藏數值模擬器來描述油藏開發生產系統，建立了油藏生產優化的最優控制模型，即最優控制函數，不同的最優控制模型會得到不同的優化結果。針對當前油田開發的實際情況，該實施例以開發期內經濟凈現值(npv)來評價聚合物驅開發效益，以npv為性能指標函數結合約束條件得出如下最優控制函數：

約束條件為：

第一約束條件為：ei(u)＝0,i∈ii(2)

第二約束條件為：ej(u)≤0,j∈ij(3)

第三約束條件為：u^low≤u≤u^up(4)

其中，j(u)表示聚合物驅的開發效益,u為注采參數對應的控制向量；l為控制時間；np為生產井數；ni為注水井數，npi為注聚井數；分別為產油、產水、注水速度及注聚量；ro、rw、rwi、rp、b分別表示原油價格、產水成本、注水成本、聚合物價格和年利率,δtⁿ為n時刻模擬計算時間步，tⁿ為n時刻累積計算時間；ei(u)表示等式約束方程；ii表示等式約束個數；ej(u)表示不等式約束方程；ij表示不等式約束個數；u^low表示控制變量下邊界值；u^up表示控制變量上邊界值。

油藏生產優化問題就是控制變量在滿足約束條件下，求取性能指標的最大值及其對應的最優控制。對于最優控制模型的求解，由于j計算公式中不顯含u，無法獲得解析梯度，而伴隨法計算又過于復雜，而蒙特卡洛梯度逼近算法(mcga)是一種簡單的有限差分梯度近似算法，每個迭代步最少僅需進行兩次數值計算即可獲得優化方向，因此，本發明實施例結合實際油藏注采參數特點，采用計算更為高效的蒙特卡洛梯度逼近算法對上述最優控制模型求解。

可選地，作為本發明的一個實施例，步驟2)中，采用協方差矩陣對所述初始擾動向量進行光滑處理和搜索方向篩選，生成目標擾動向量。

步驟2)中的蒙特卡洛梯度逼近算法的基本思想是：

首先，利用蒙特卡洛法在當前控制變量周圍生成若干個隨機變量的實現；

然后，分別求取各隨即變量實現所對應的目標函數值；

最后，利用各實現及其目標函數值來估計目標函數的梯度。

在利用蒙特卡洛逼近算法時，首先會在第l迭代步的控制變量附近生成擾動向量，現有技術的蒙特卡洛逼近算法通常直接采用這個擾動向量進行求解，而本實施例則采用協方差矩陣對所述擾動向量進行光滑處理和搜索方向篩選后，采用生成的目標擾動向量進行求解，從而使近似梯度與真實梯度夾角更小、更接近于真實梯度，達到加快收斂速度、提高算法的收斂速度的目的。

具體的，協方差矩陣由球形模型進行定義，表達式為：

其中，σ是擾動向量的標準方差，表示時間關聯程度；m和n分別表示時間和步數；t表示時間步數預設閾值。協方差矩陣是一個方塊對角矩陣，其特殊的形式是由于考慮了單井的時間關聯性，其表達式為：

接下來對協方差矩陣進行喬里斯基分解，分解后滿足等式：

式中，為下三角矩陣，表示的轉置；進而定義目標擾動向量δ為:

其中，z為服從標準正態分布的nu維初始擾動向量。

可選地，作為本發明的一個實施例，步驟3)中對最優控制函數進行求解具體過程如下：

3.1)生成優化參數以及迭代步l等于0對應的第一控制變量u^l；其中，優化參數包括迭代步長和擾動常數。

3.2)采用對數變換方法將第一控制變量u^l轉換為第三約束條件對應的無約束優化條件下的第二控制變量s^l。

其中，具體轉換過程為：

主要是對于邊界約束公式(4)，采用對數變換方法，將邊界約束轉換為無約束優化問題，具體公式如下。

以上公式即為第一公式，其中，表示變換后的第i個控制變量；；表示變量u在第l^th迭代步下的第i^th個控制分量，表示上界，表示下界。利用對數變換方法，值域從正無窮變為負無窮，相應的約束優化問題被轉換成了無約束優化問題，接下來的優化以為對象，且變換回公式如下：

3.3)將第二控制變量s^l帶入到最優控制函數中，生成對應的第一函數值j(s^l)；

3.4)利用包括目標擾動向量和優化參數的蒙特卡洛算法求取最優控制函數在第二控制變量s^l處的蒙特卡洛梯度，具體的求解過程為：

3.4.1)在蒙特卡洛梯度逼近算法的計算過程中，在第l個迭代步，生成了nr個目標函數值，即用于計算近似梯度。設δj^j為第j個擾動向量s^l,j生成的目標函數值與當前最優控制變量s^l所對應的目標函數值之差，則δj^j的表達式為：

δj^j＝j(s^l,j)-j(s^l)＝j(s^l,j+ε·δ^l,j)-j(s^l)j＝1,2...,nr(11)

3.4.2)在第l個迭代步，令第j個擾動向量的第i(i＝1,2,...,nu)個元素為則蒙特卡洛梯度為：

3.5)根據投影梯度優化方法，采用優化參數和步驟3.4)計算出的蒙特卡洛梯度，將第二控制變量s^l轉換為滿足第一約束條件和第二約束條件的第三控制變量s^l+1。該步驟具體的計算過程如下：

針對油藏開發實際情況而言，現場的注水量、采出量變化不宜過大，因此對控制變量進一步采用了等式和不等式約束的約束條件進行約束，即公式(2)～(3)。對于等式約束和不等式約束，采用了投影梯度優化方法進行處理。投影梯度優化方法是：當迭代點在可行域的內部時，以該點的負梯度方向為下降可行方向；而當迭代點位于可行域的邊界上且其梯度方向指向可行域外部時，則取它的負梯度方向在邊界上的投影為下降可行方向，若這個投影為零向量，則停止迭代，得到問題的極小點。

投影梯度優化方法的優化過程包括投影移動和歸位移動兩個過程。設在第l個迭代步，對于s^l有ns個激活的約束條件，其所組成的激活約束向量為ea，設其元素ea,i(i＝1,2,…,ns)為優化控制模型中的第s個約束條件，即

ea,i＝es(u^l)≥0，s∈ii∪ij(13)

其中，u^l為s^l對應的真實控制變量。那么，對于s^l進行更新的投影移動計算公式為：

式中，α為迭代步長；p為nu維投影矩陣：

式中，i為nu維單位陣；為由激活約束對s^l的梯度所組成矩陣，其第i列向量表達式為：

對于非線性約束問題，進行投影移動后變量s^l+1通常會越過邊界，因此需要進行歸位移動計算。但是在s^l處進行歸位計算的方法在實際應用中進行一次歸位計算可能難以滿足全部約束，為此這里采用迭代歸位移動的求解方法。

設在s^l+1處有ns'個激活的約束，其組成的激活約束向量為ea′，將向量在s^l+1處進行線性展開可得，

令求取β為

從而s^l+1進行歸位可得，

其中，為ea′對s^l+1的梯度所組成的矩陣，β為ns'維向量。根據公式(19)，對s^l+1進行迭代歸位移動計算的表達式為：

式中，n是歸位移動中迭代的步數。以上公式(14)即為無需歸位移動時對應的第二公式，公式(20)為需要歸位移動時對應的第二公式。

3.6)計算第三控制變量s^l+1對應的第二函數值，并比較第二函數值和第一函數值，若第二函數值大于第一函數值，則將第三控制變量s^l+1設定為目標控制變量，然后執行步驟3.7)；否則，將迭代步長減半，并返回至步驟3.5)。

3.7)判斷第二函數值是否滿足預設的收斂條件，若滿足，則輸出第二函數值為最優開發效益,輸出目標控制變量為最優注采參數對應的控制向量；若不滿足，則令迭代步加1，并返回至步驟3.2)；或者判斷迭代次數是否達到預設的最大迭代次數，若是，則輸出第二函數值為最優開發效益,輸出目標控制變量為最優注采參數對應的控制向量，若否，則令迭代步加1，并返回至步驟3.2)。其中，收斂條件為：

公式(21)和(22)中，ξ為預設極小常數。

實施例：

本實施例的模型區塊是一個典型的含高滲帶地層，網格數為21×21×1，網格長度均為50m，厚度為20m。平均孔隙度和滲透率分別為949md和0.25，初始含油飽和度為0.67，初始油藏壓力為10.426mpa。如圖2a所示，為采用現有技術聚合物驅生產優化方法，即采用標準蒙特卡洛逼近方法優化后的歸一化梯度圖，而圖2b為本發明采用改進后的蒙特卡洛逼近方法優化后的歸一化梯度圖，結合圖2a和圖2b可以看到，采用本發明的優化方法得到的梯度更接近真實梯度，因此優化效率更高，收斂速度更快。如圖3所示，展示了該模型區塊的滲透率場，可見該模型為一注四采5點法井網，其中分別有兩口井分布在高滲帶和低滲區。原生產方案在高產井含水率約91％時開始注入聚合物，注聚時間為900天，總模擬時間為4200天。對原生產方案進行生產優化時，其中設置的邊界約束條件為：高產井為0到200m³/天，低產井為0到70m³/天，注水井為0到600m³/天，聚合物濃度為0到4kg/m³。

圖4為npv的優化結果，橫坐標表示迭代次數。如圖4所示，在約20次迭代后，本發明改進后的蒙特卡洛梯度逼近算法優化結果收斂，而現有技術的標準蒙特卡洛梯度逼近算法的npv仍然在緩慢增加，需要約30次迭代，且其優化后的值始終低于本發明算法。經過優化，npv值在原始生產制度的基礎上增加了約21％。由此可見本發明的蒙特卡洛梯度逼近算法具有較高的計算效率。

圖5為優化前后的區塊含水率對比結果，由圖5可見，本發明改進后的蒙特卡洛梯度逼近算法的區塊含水率下降至77％，比優化前下降了約5％；而現有技術的標準蒙特卡洛梯度逼近算法的區塊含水率只下降到了80％，由此可見本發明的算法具有更好的優化表現。

圖6a～6c為優化前后的飽和度場對比結果圖，可以看到經過本發明蒙特卡洛梯度逼近算法的優化，在注水井周圍的網格的注入水流動到了更廣的區域，同時從注水井到低產井方向上也有更多的網格含油飽和度降低，高產井周邊的網格含油飽和度也進一步下降。與現有技術的標準蒙特卡洛梯度逼近算法相比，現有技術在注水井附近網格含水飽和度更高，說明本發明算法的波及效果更好。因此說明了本發明的蒙特卡洛梯度逼近算法具有較好的優化效果。

圖7為注聚濃度的優化結果，圖8為段塞大小的優化結果，從圖7和圖8中可以看到，本發明改進后蒙特卡洛梯度逼近算法的優化結果比現有算法的優化結果具有更強的波動性，也得到了更好的優化結果。

圖9為注水量的優化結果，圖10a、圖10b為產液量的優化結果，如圖9、圖10a、圖10b所示，與注聚濃度和段塞大小的優化結果類似，本發明蒙特卡洛梯度逼近算法的優化結果具有更強的規律性，而現有算法，特別是從圖10b可以看出，其值均在某個值附近隨機增減，導致最終的優化效果不佳，由此也說明了本發明的蒙特卡洛梯度逼近算法具有更好的優化效果。

如圖11所示，本發明還提供一種基于蒙特卡洛算法的聚合物驅生產優化系統，其包括模型建立模塊、擾動向量生成模塊和優化模塊。其中：

模型建立模塊用于根據油藏數值模擬器生成油藏優化的最優控制函數，最優控制函數的輸入為注采參數對應的控制向量，輸出為聚合物驅的開發效益；

擾動向量生成模塊用于生成協方差矩陣和初始擾動向量，并采用協方差矩陣對初始擾動向量進行處理，生成目標擾動向量；

優化模塊用于采用包括目標擾動向量的蒙特卡洛算法對最優控制函數進行求解，生成最優開發效益對應的最優注采參數。

可選的，在本發明的一個優選實施例中，采用開發期內經濟凈現值npv表示聚合物驅的開發效益，最優控制函數具體為：

第一約束條件為：ei(u)＝0,i∈ii；

第二約束條件為：ej(u)≤0,j∈ij；

第三約束條件為：u^low≤u≤u^up；

其中，j(u)表示聚合物驅的開發效益,u為注采參數對應的控制向量；l為控制時間；np為生產井數；ni為注水井數，npi為注聚井數；分別為產油、產水、注水速度及注聚量；ro、rw、rwi、rp、b分別表示原油價格、產水成本、注水成本、聚合物價格和年利率,δtⁿ為n時刻模擬計算時間步,tⁿ為n時刻累積計算時間。

在另一優選實施例中，擾動向量生成模塊中采用協方差矩陣對初始擾動向量進行光滑處理和搜索方向篩選，生成目標擾動向量。

可選的，在本發明的一個優選實施例中，優化模塊包括第一生成單元、第一變換單元、第一計算單元、第二計算單元、第二變換單元、比較單元和收斂判斷單元。其中：

第一生成單元，用于生成優化參數以及迭代步l等于0對應的第一控制變量u^l，優化參數包括迭代步長和擾動常數；

第一變換單元，用于采用對數變換方法將第一控制變量u^l轉換為第一約束條件對應的無約束優化條件下的第二控制變量s^l；

第一計算單元，用于將第二控制變量s^l帶入到最優控制函數中，生成對應的第一函數值；

第二計算單元，用于利用包括目標擾動向量和優化參數的蒙特卡洛算法求取最優控制函數在第二控制變量s^l處的蒙特卡洛梯度；

第二變換單元，用于根據投影梯度優化方法，采用優化參數和所述蒙特卡洛梯度，將第二控制變量s^l轉換為滿足第二約束條件和第三約束條件的第三控制變量s^l+1；

比較單元，用于將第三控制變量s^l+1帶入到最優控制函數中，生成對應的第二函數值；并比較第二函數值和第一函數值，若第二函數值大于第一函數值，則將第三控制變量s^l+1設定為目標控制變量，否則，將迭代步長減半，并驅動第二變換單元生成新的第三控制變量s^l+1；

收斂判斷單元，用于判斷第二函數值是否滿足預設的收斂條件，若是，則輸出第二函數值為最優開發效益，輸出目標控制變量為最優注采參數對應的控制向量，若否，則令迭代步加1，并驅動第一變換單元；或者收斂單元用于判斷迭代次數是否達到預設的最大迭代次數，若是，則輸出第二函數值為最優開發效益，輸出目標控制變量為最優注采參數對應的控制向量，若否，則令迭代步加1，并驅動第一變換單元開始下一次迭代過程。

在本實施例中，第一變換單元具體用于利用第一預設公式將第一控制變量u^l轉換為所述第一約束條件對應的無約束優化條件下的第二控制變量s^l；

第二變換單元具體用于利用第二預設公式將第二控制變量s^l轉換為滿足第二約束條件和第三約束條件的第三控制變量s^l+1。

綜上所述，本發明建立了一種考慮注采量相關性的基于蒙特卡洛梯度逼近算法的油藏生產優化方法。現階段，各大油田均進入開發的中后期，含水率不斷上升，單純的使用水驅已經不能進一步提高采收率；同時作為三次采油的一種重要方法，聚合物驅在制定方案時多利用正交設計等方法，方案往往不是最優。本發明針對以上的一些問題，提出了一套新的可應用于聚合物驅的生產優化方法。本發明首先基于聚合物驅方法建立了新的優化模型，同時引入了協方差矩陣對蒙特卡洛梯度逼近算法進行了改進。蒙特卡洛梯度逼近算法是一種無梯度類算法，具有算法步驟簡單，容易實現，同時具有易于與商業油藏模擬器結合的特點。最后在實施例中，使用了一含高滲條帶的一注四采模型對本方法進行了驗證，其結果顯示改進后的蒙特卡洛梯度逼近算法比其標準算法效率更高，因而證明了本發明的方法具有更高的計算效率與實用價值。由于水驅可以視為聚合物驅的一種特殊情況，即注入聚合物濃度為0的情況，因此本發明依然可用于解決水驅優化問題，具有較廣泛的適用性，對本發明進行適當改進，可以進一步推廣到其他的三次采油方法中。

在本發明的描述中，需要理解的是，術語“第一”、“第二”僅用于描述目的，而不能理解為指示或暗示相對重要性或者隱含指明所指示的技術特征的數量。由此，限定有“第一”、“第二”的特征可以明示或者隱含地包括至少一個該特征。在本發明的描述中，“多個”的含義是至少兩個，例如兩個，三個等，除非另有明確具體的限定。

在本說明書的描述中，參考術語“一個實施例”、“一些實施例”、“示例”、“具體示例”、或“一些示例”等的描述意指結合該實施例或示例描述的具體特征、結構、材料或者特點包含于本發明的至少一個實施例或示例中。在本說明書中，對上述術語的示意性表述不必須針對的是相同的實施例或示例。而且，描述的具體特征、結構、材料或者特點可以在任一個或多個實施例或示例中以合適的方式結合。

此外，在不相互矛盾的情況下，本領域的技術人員可以將本說明書中描述的不同實施例或示例以及不同實施例或示例的特征進行結合和組合。凡根據本發明原理進行的改進和等同變換，均不應排除在本發明的保護范圍之外。