本發(fā)明涉及一種基于加權(quán)修正參數(shù)的P范數(shù)高分辨率高精度噪聲源定位識別方法，屬于噪聲源定位技術(shù)領(lǐng)域。

背景技術(shù)：

常規(guī)波束形成(conventional beamforming，CBF)作為最主要的噪聲源陣列信號處理技術(shù)因其優(yōu)良的寬容性和易操作性被廣泛的應(yīng)用到對飛機，汽車輻射噪聲的探測與定位中。然而常規(guī)波束形成其空間分辨率受到陣列物理孔徑的限制，即存在“瑞利限(Rayleigh)”，在多聲源探測中，空間“混淆”問題嚴重。

為了突破“瑞利限”，眾多高分辨率譜估計法應(yīng)運而生，其中以子空間多重信號分類(MUSIC)算法為代表，該算法通過對基陣接收數(shù)據(jù)協(xié)方差矩陣進行特征分解，從而得到同信號分量相對應(yīng)的信號子空間與噪聲子空間,利用其正交特性構(gòu)造出“針狀”空間譜峰，相較于以往的各種方法大大的提高了定位精度及空間分辨率。然而該方法僅能得到聲源方位的估計結(jié)果，無法真實反映聲源貢獻的相對大小，不能達到聲源識別的目的。

技術(shù)實現(xiàn)要素：

針對上述問題，本發(fā)明要解決的技術(shù)問題是提供一種基于加權(quán)修正參數(shù)的P范數(shù)高分辨率高精度噪聲源定位識別方法。

本發(fā)明的基于加權(quán)修正參數(shù)的P范數(shù)噪聲源定位識別方法，它的定位識別方法為：

步驟一、特征值分解聲源定位識別方法：

由M元全向聲學麥克風陣列接收數(shù)據(jù)構(gòu)造的譜矩陣為：

其中：P(ω)＝[P₁(ω) P₂(ω)L P_M(ω)]^T為陣列接收信號進行離散傅里葉變換后的頻域快拍矢量,上標H表示共軛轉(zhuǎn)置；由于為Hermite矩陣,其特征值分解可表示成：

其中Λ是一個對角矩陣，由排序的特征值組成：

Λ＝diag[λ₁,λ₂,L,λ_M] (3)

U為M×M維矩陣,由正交特征矢量組成：

U＝[φ₁ Mφ₂ ML Mφ_M] (4)

每個正交特征矢量定義了一個特征子空間，表示陣列對信號在該子空間內(nèi)響應(yīng)的方向向量，其特征值為子空間響應(yīng)強度；由此通過特征值及特征失量來定義陣列對聲源在該子空間內(nèi)的響應(yīng)函數(shù)為：

將u_i帶入式(2)得到由子空間響應(yīng)函數(shù)表征的譜矩陣為：

由于特征子空間與特征矢量具有相同的正交特性,上式可寫成：

比較式(1)和式(7)發(fā)現(xiàn)陣列對空間聲源的響應(yīng)可表示成各階特征子空間響應(yīng)函數(shù)的疊加；若S_i為第i階特征子空間對應(yīng)的i階聲源向量，H為聲源向量與接收陣元間的傳遞函數(shù)矩陣，那么每階特征子空間均可看成是一個網(wǎng)絡(luò)系統(tǒng)，其輸出為子空間響應(yīng)函數(shù)u_i：

HS_i＝u_i (8)

由于聲波是微振幅波,滿足疊加原理，當輸入為時疊加原理確認網(wǎng)絡(luò)的輸出為即陣列對空間聲源的響應(yīng)，那么由網(wǎng)絡(luò)系統(tǒng)傳遞特性可知，此時輸入信號就表示掃描空間中待識別的目標聲源；

步驟二、P范數(shù)噪聲源信號重構(gòu)法：

首先將掃描域離散化為N個格點區(qū)域，節(jié)點處為波束掃描點，各掃描點均存在一預設(shè)聲源，除目標聲源外，其余為假想聲源，所有預設(shè)聲源幅值構(gòu)成了子空間內(nèi)(T·N)×1維聲源向量S_i，T表示預設(shè)聲源類型數(shù)；

認為該子空間響應(yīng)函數(shù)u_i是由這些預設(shè)源輻射的聲場疊加產(chǎn)生,不同預設(shè)聲源類型聯(lián)合構(gòu)成了掃描點與陣元間的M×(T·N)維傳遞函數(shù)矩陣H，通過求解式(8)可計算出聲源向量S_i,即該子空間內(nèi)波束掃描輸出；考慮式(8)為聲學逆問題,通常采用正則化技術(shù)獲得問題的近似解；

其中α稱為正則化參數(shù)；其取值與輸入的信噪比有關(guān)，通常為矩陣HH^-1(或H^-1H)最大特征值的0.1％～10％；

由于假想聲源并不真實存在，其幅值在向量S_i表現(xiàn)為零或近似為零，采用基于加權(quán)修正參數(shù)的P范數(shù)迭代算法，將式(8)轉(zhuǎn)化為如下線性約束優(yōu)化問題；

其中p的取值范圍為0到1之間，分別代表不同的范數(shù)約束；E_(p)(S_i)越小說明S_i中的信息越局部化，越稀疏；采用Lagrange乘子的方法求解上式，要最小化的代價函數(shù)為：

其中λ為Lagrange乘子向量，對S_i和λ分別求復梯度并求解，得到：

由(12)式可得：

進而可解出關(guān)于聲源向量S_i和Lagrange乘子λ的形式解如下：

其中W＝diag(|S_i(n)|^P-2)；由于式(14)是一個非線性方程，因此需要采用迭代方法求解S_i；將W作為迭代加權(quán)矩陣，其取值為前一次迭代結(jié)果構(gòu)成的對角陣，代入公式(14)獲得新一代的S_i，由其構(gòu)成的W作為下一代加權(quán)矩陣，如此反復直至達到最優(yōu)解為止；考慮到矩陣HW^-1H^H通常為病態(tài)的，需要在每次迭代過程中引入正則化參數(shù)降低重構(gòu)誤差；綜上得到求解聲源向量S_i的迭代公式如下：

其中(k)表示迭代次數(shù)，同理可獲得每次迭代的代價函數(shù)為：

由于聲源向量S_i信息局部化的特點，在每次的迭代過程中都會有部分元素值為零，將這些元素代入加權(quán)矩陣W中時所對應(yīng)的加權(quán)值同樣為零，這樣使得在中為零的元素在中依然為零；并將加權(quán)矩陣W加以修正：

W＝diag(|S_i(n)|^P-2+ε) (17)

步驟三、加權(quán)修正參數(shù)ε對算法的選取：

在掃描空間中隨機分布25個單極子聲源，滿足N/κ＝100/25＝4>3的稀疏條件，發(fā)射頻率f＝2kHz，分別討論了聲源強度均值為0.1、1、10時參數(shù)ε對聲源向量重建精度的影響，ε的變化范圍0.001～5，共進行25次迭代，50次Monte-carlo仿真試驗；

最后加權(quán)修正參數(shù)的大小與聲場信息有關(guān)：

其中表示加權(quán)迭代前由(9)式直接計算的結(jié)果。

與現(xiàn)有技術(shù)相比，本發(fā)明的有益效果為：通過特征分解獲得各階特征子空間及子空間響應(yīng)函數(shù)，對各階特征子空間采用預設(shè)聲源的方法建立子空間聲源向量重構(gòu)模型，利用加權(quán)修正參數(shù)的P范數(shù)稀疏性約束求解該重構(gòu)模型，迫使子空間聲源向量能更快，更有效的向真實稀疏源位置收斂，獲得能量更加集中的稀疏解；分析了信噪比、測量距離、基陣孔徑及分析頻率對算法定位性能的影響，仿真結(jié)果顯示該方法可實現(xiàn)對不同類型聲源位置及幅度的準確估計，穩(wěn)定性較好。

附圖說明

為了易于說明，本發(fā)明由下述的具體實施及附圖作以詳細描述。

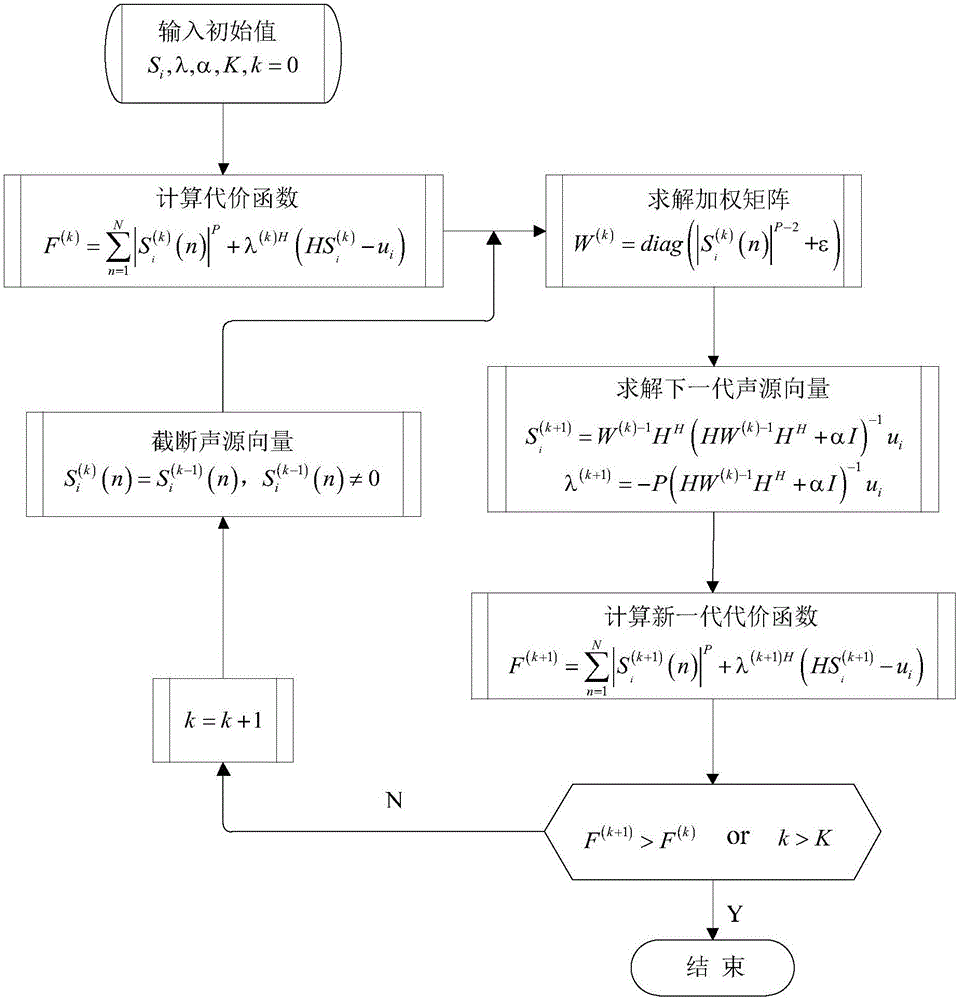
圖1為本發(fā)明的流程圖；

圖2為本發(fā)明中P-EVD性能與ε及信號均值關(guān)系曲線圖；

圖3為本發(fā)明中新的ε對P-EVD性能的影響示意圖；其中a為ε與聲源強度關(guān)系曲線圖；b為聲源強度均值與重建精度關(guān)系曲線圖；

圖4為實施例中非相干單極子聲源定位示意圖，其中a為CBF；b為MUSIC；c為P-EVD；

圖5為實施例中相干單極子聲源定位示意圖；其中a為CBF；b為MUSIC；c為P-EVD；

圖6為實施例中分布式聲源定位示意圖；其中a為CBF；b為MUSIC；c為P-EVD；

圖7為實施例中混合類型聲源定位示意圖；其中a為CBF單極子；b為CBF偶極子；c為MUSIC單極子；d為MUSIC-偶極子；e為P-EVD單極子；f為P-EVD偶極子；

圖8為實施例中頻率對聲源定位性能的影響示意圖；其中a為幅度估計誤差；b為方位估計誤差；

圖9為實施例中測距孔徑比對聲源定位性能的影響示意圖；其中a為幅度估計誤差；b為方位估計誤差；

圖10為實施例中噪聲對聲源定位性能的影響示意圖；其中a為幅度估計誤差；b為方位估計誤差。

具體實施方式

為使本發(fā)明的目的、技術(shù)方案和優(yōu)點更加清楚明了，下面通過附圖中示出的具體實施例來描述本發(fā)明。但是應(yīng)該理解，這些描述只是示例性的，而并非要限制本發(fā)明的范圍。此外，在以下說明中，省略了對公知結(jié)構(gòu)和技術(shù)的描述，以避免不必要地混淆本發(fā)明的概念。

如圖1所示，本具體實施方式采用以下技術(shù)方案：它的定位識別方法為：

一、特征值分解聲源定位識別方法：

考慮由M元全向聲學麥克風陣列接收數(shù)據(jù)構(gòu)造的譜矩陣為：

其中：P(ω)＝[P₁(ω) P₂(ω)L P_M(ω)]^T為陣列接收信號進行離散傅里葉變換后的頻域快拍矢量,上標H表示共軛轉(zhuǎn)置。由于為Hermite矩陣,其特征值分解(EVD)可表示成：

其中Λ是一個對角矩陣，由排序的特征值組成：

Λ＝diag[λ₁,λ₂,L,λ_M] (3)

U為M×M維矩陣,由正交特征矢量組成：

U＝[φ₁ Mφ₂ ML Mφ_M] (4)

每個正交特征矢量定義了一個特征子空間，表示陣列對信號在該子空間內(nèi)響應(yīng)的方向向量，其特征值為子空間響應(yīng)強度；由此可以通過特征值及特征失量來定義陣列對聲源在該子空間內(nèi)的響應(yīng)函數(shù)為：

將u_i帶入式(2)得到由子空間響應(yīng)函數(shù)表征的譜矩陣為：

由于特征子空間與特征矢量具有相同的正交特性,上式可寫成：

比較式(1)和式(7)發(fā)現(xiàn)陣列對空間聲源的響應(yīng)可表示成各階特征子空間響應(yīng)函數(shù)的疊加。若S_i為第i階特征子空間對應(yīng)的i階聲源向量，H為聲源向量與接收陣元間的傳遞函數(shù)矩陣，那么每階特征子空間均可看成是一個網(wǎng)絡(luò)系統(tǒng)，其輸出為子空間響應(yīng)函數(shù)u_i：

HS_i＝u_i (8)

由于聲波是微振幅波,滿足疊加原理，當輸入為時疊加原理確認網(wǎng)絡(luò)的輸出為即陣列對空間聲源的響應(yīng)，那么由網(wǎng)絡(luò)系統(tǒng)傳遞特性可知，此時輸入信號就表示掃描空間中待識別的目標聲源。至此，對空間目標聲源的探測定位被轉(zhuǎn)化為求解各階特征子空間內(nèi)的聲源向量問題。

二、P范數(shù)噪聲源信號重構(gòu)法(P-EVD)：

與常規(guī)波束形成聲源定位識別方法相同,對于任意階特征子空間,首先將掃描域離散化為N個格點區(qū)域，節(jié)點處為波束掃描點，各掃描點均存在一預設(shè)聲源,該預設(shè)聲源可以是點聲源，偶極子聲源，多極子聲源等,也可為不同類型聲源的組合形式。除目標聲源外，其余為假想聲源，所有預設(shè)聲源幅值構(gòu)成了子空間內(nèi)(T·N)×1維聲源向量S_i，T表示預設(shè)聲源類型數(shù)。認為該子空間響應(yīng)函數(shù)u_i是由這些預設(shè)源輻射的聲場疊加產(chǎn)生,不同預設(shè)聲源類型聯(lián)合構(gòu)成了掃描點與陣元間的M×(T·N)維傳遞函數(shù)矩陣H，通過求解式(8)可計算出聲源向量S_i,即該子空間內(nèi)波束掃描輸出；考慮式(8)為聲學逆問題,通常采用正則化技術(shù)獲得問題的近似解。

其中α稱為正則化參數(shù)；其取值與輸入的信噪比有關(guān),通常為矩陣HH^-1(或H^-1H)最大特征值的0.1％～10％。

由于假想聲源并不真實存在，其幅值在向量S_i表現(xiàn)為零或近似為零，而目標聲源通常具有較大的幅值，這說明S_i具有信息局部化的特點，可將其看成是一組稀疏信號。正則化技術(shù)雖然解決了逆問題的不適定性，但并不能獲得最優(yōu)的稀疏解。為了得到能量集中的稀疏解,采用基于加權(quán)修正參數(shù)的P范數(shù)迭代算法，將式(8)轉(zhuǎn)化為如下線性約束優(yōu)化問題。

其中p的取值范圍為0到1之間，分別代表不同的范數(shù)約束。E_(p)(S_i)越小說明S_i中的信息越局部化，越稀疏。采用Lagrange乘子的方法求解上式，要最小化的代價函數(shù)為：

其中λ為Lagrange乘子向量，對S_i和λ分別求復梯度并求解，得到：

由(12)式可得：

進而可解出關(guān)于聲源向量S_i和Lagrange乘子λ的形式解如下：

其中W＝diag(|S_i(n)|^P-2)。由于式(14)是一個非線性方程，因此需要采用迭代方法求解S_i。將W作為迭代加權(quán)矩陣，其取值為前一次迭代結(jié)果構(gòu)成的對角陣，代入公式(14)獲得新一代的S_i，由其構(gòu)成的W作為下一代加權(quán)矩陣，如此反復直至達到最優(yōu)解為止。考慮到矩陣HW^-1H^H通常為病態(tài)的，需要在每次迭代過程中引入正則化參數(shù)降低重構(gòu)誤差。綜上得到求解聲源向量S_i的迭代公式如下：

其中(k)表示迭代次數(shù)，同理可獲得每次迭代的代價函數(shù)為：

由于聲源向量S_i信息局部化的特點，在每次的迭代過程中都會有部分元素值為零，可以注意到，將這些元素代入加權(quán)矩陣W中時所對應(yīng)的加權(quán)值同樣為零，這樣使得在中為零的元素在中依然為零。這樣會導致聲源向量S_i部分信息缺失，鑒于此，將加權(quán)矩陣W加以修正：

W＝diag(|S_i(n)|^P-2+ε) (17)

三、加權(quán)修正參數(shù)ε對算法的選取：

由前面的分析可知，加權(quán)修正參數(shù)的引入是為了避免聲源向量中的信息丟失，確保迭代過程的穩(wěn)健性。因此計算過程中參數(shù)ε的參與勢必會影響算法的性能。加權(quán)修正參數(shù)的選取對聲源向量重建精度的影響很大，選擇適當?shù)男拚齾?shù)不僅可以提高重建精度還可以增加空間中可識別的聲源數(shù)目。下面討論參數(shù)ε對算法的影響。

在掃描空間中隨機分布25個單極子聲源，滿足N/κ＝100/25＝4>3的稀疏條件，發(fā)射頻率f＝2kHz，分別討論了聲源強度均值為0.1、1、10時參數(shù)ε對聲源向量重建精度的影響，ε的變化范圍0.001～5，共進行25次迭代，50次Monte-carlo仿真試驗。

圖2中顯示了聲源強度均值不同時，加權(quán)修正參數(shù)ε對P-EVD性能的影響，可以發(fā)現(xiàn)修正參數(shù)ε對聲源向量重建精度的影響與聲源強度均值有關(guān)，對于相同的修正參數(shù)，信號強度均值越小，重建精度越高；當信號強度均值一定時，隨著參數(shù)ε的增加重建精度降低，P-EVD算法的性能下降。為了使參數(shù)的選擇更具有通用性，滿足強信號對應(yīng)小參數(shù)的條件，將加權(quán)修正參數(shù)做如下更改，不再是按經(jīng)驗選取的固定值，其大小與聲場信息有關(guān)：

其中表示加權(quán)迭代前由(9)式直接計算的結(jié)果。為了驗證上式參數(shù)的有效性，采用同圖1相同的仿真條件，分析在新的加權(quán)修正參數(shù)下，聲源強度均值與重建精度的關(guān)系及不同聲源強度均值對應(yīng)的ε值。

圖3顯示了式(18)中新的加權(quán)修正參數(shù)ε對P-EVD定位性能的影響。由圖3(a)可見，隨著聲源強度的增加，參數(shù)ε值越來越小，這與圖2中顯示的結(jié)果相同，再次證明了聲源信號越強，所需的加權(quán)修正參數(shù)值越小。圖3(b)顯示的是采用圖(a)中的參數(shù)ε進行加權(quán)疊加計算聲源強度與聲源向量重建精度的關(guān)系。將圖中曲線與圖3中的結(jié)果進行比較，可見在新的加權(quán)修正參數(shù)ε下，無論聲源強度為何值，聲源向量重建成功率均達到99％以上，說明如式(18)顯示的加權(quán)修正參數(shù)ε具有自適應(yīng)性。在實際測量中，可以采用該參數(shù)ε進行加權(quán)疊加計算來提高算法的性能。

實施例：

仿真分析：

為了基于加權(quán)修正參數(shù)的P范數(shù)噪聲源定位算法(P-EVD)的有效性,將其對不同類型聲源的定位識別結(jié)果與經(jīng)典的常規(guī)波束形成技術(shù)(CBF)和子空間MUSIC算法進行比較分析；采用由聲學麥克風構(gòu)成的7×7均勻網(wǎng)格陣，陣元間距0.3m；目標聲源位于x-y平面上,掃描域8m×8m；掃描間隔0.25m；基陣面與掃描面相距z＝5m；背景噪聲為高斯白噪聲,除特別說明，信噪比snr＝20dB；Monte-Carlo實驗數(shù)為50；取P＝1；正則化參數(shù)α取最大特征值的1％。

考慮到噪聲源大多可看成是由單極子或偶極子構(gòu)成的分布式聲源,故預設(shè)聲源采用單極子聲源及任意方向的偶極子聲源,其頻域表達式如下：

其中,表示聲源與陣元間的方向矢量，θ為偶極子方向即偶極子軸與x軸的夾角，由于x-y平面上任意方向的偶極子可由位于θ＝0°和θ＝90°的偶極子表示，因此預設(shè)聲源類型可設(shè)定為x方向θ＝0°的偶極子聲源,y方向θ＝90°的偶極子聲源及單極子點聲源，下面分別對不同形式的聲源進行仿真分析。

算例一：兩個非相干單極子聲源A和B分別位于(-1,0,0)和(1,0,0)，發(fā)射頻率為1.5kHz幅值為a_A＝a_B＝2的單頻信號。

圖4所示是三種算法對非相干單極子聲源的定位結(jié)果，由于常規(guī)波束形成算法的空間分辨率低,并且旁瓣起伏較大(圖4(a)),從掃描圖中不能分辨出兩個聲源的空間位置；圖4(b)中的MUSIC算法是一種高分辨率空間譜估計算法,其空間分辨率明顯高于CBF,具有尖銳的聚焦峰和低旁瓣級,圖中兩聲源空間位置清晰可見,該方法可實現(xiàn)對非相干聲源的準確定位；但對聲源幅值的估計不盡理想(圖中兩聲源幅值為a_A＝a_B＝0.055),這是由于MUSIC空間譜估計算法是利用信號子空間與噪聲子空間的正交性估計目標聲源方位；并不能獲得目標聲源的幅值；由上闡述可知P-EVD算法是以P范數(shù)為約束獲得信號能量高度集中的稀疏解,因此在完成對聲源精確定位的基礎(chǔ)上還可實現(xiàn)對聲源幅值的估計,使這一問題得以解決；圖4(c)顯示的是采用P-EVD算法輸出的空間譜,圖中無旁瓣,具有更尖銳的聚焦峰尺度,聲源位置清晰可見,可獲取高精度高分辨率聲源定位結(jié)果.圖中顯示兩聲源幅值為a_A＝a_B＝2.08,估計誤差為4％,估計精度良好；在誤差允許范圍內(nèi),該方法可獲得對聲源方位及幅值滿意的估計結(jié)果。

算例二：考慮兩相干單級子聲源A和B,其聲源參數(shù)同算例一。

從圖5顯示的結(jié)果可以看出：(1)與算例一的仿真結(jié)果相似，CBF的低分辨率使其依然無法分辨出聲源的個數(shù)及空間位置,定位失效。(2)雖然MUSIC算法在非相干聲源定位中展現(xiàn)出高分辨率的優(yōu)越性，但對于相干聲源,由于無法準確估計聲源個數(shù)，因此很難實現(xiàn)對相干聲源的檢測(圖5(b))，其定位結(jié)果同樣失效。(3)P-EVD算法依然具有優(yōu)異的空間分辨率和精確的幅度估計能力,a_A＝a_B＝1.99，其幅度估計誤差為1％,克服了其他方法不能處理相干聲源的不足。算例一同算例二說明P-EVD方法可實現(xiàn)對聲源位置及幅度的精確估計而無需考慮其相干性。

算例三：目標聲源為兩條聲源中心分別位于(-1,1.5,0)和(1,-0.8,0)的非相干有限長線源A和B，與x軸夾角分別為45°和90°,其長度均為1.4m,發(fā)射頻率為1.5kHz聲源幅度a_A＝a_B＝1的單頻信號,將其看成是由多個單極子聲源構(gòu)成的分布式聲源。掃描結(jié)果如圖6所示,分布式聲源由圖中＊標注。

結(jié)果顯示：(1)CBF與MUSIC對分布式聲源的掃描輸出看起來更像是兩個集中聲源，MUSIC算法僅僅是消除了CBF中大部分的旁瓣干擾，提高了空間分辨率，依然不能獲得精準的定位結(jié)果及幅度估計。(2)P-EVD的掃描結(jié)果與圖中標定的分布式聲源吻合的很好，輸出聲源幅度為a_A＝a_B＝0.99,估計誤差1％。通過該仿真可知，該方法可實現(xiàn)對分布式聲源形態(tài)，方向，位置的有效識別及其幅度的準確估計。

算例四：偶極子聲源A位于(1,1,0),其偶極子軸與x方向夾角為45°±180°,在(-2,-1,0)處同時存在與聲源A相干的單極子聲源B,兩聲源均發(fā)射頻率為1.5kHz,幅度a_A＝a_B＝1的單頻信號。

當空間同時存在單極子和偶極子聲源時，根據(jù)預設(shè)的聲源類型,陣列掃描結(jié)束后可同時獲得單極子聲源模型與偶極子聲源模型的輸出結(jié)果,如圖7所示，圖中箭頭標記顯示為聲場梯度,用以判斷偶極子方向。圖7(a)中CBF對單極子模型及偶極子模型的掃描輸出相似，掃描結(jié)果均顯示存在兩個峰值，雖然在偶極子掃描結(jié)果中聲場梯度與聲源A的方向相同,但僅從這兩張掃描圖無法判斷聲源個數(shù)及類型,進而無法實現(xiàn)聲源識別。盡管MUSIC算法有較好的偶極子掃描結(jié)果,但目標源的相干性造成MUSIC算法對單極子模型的掃描結(jié)果在偶極子聲源A處出現(xiàn)峰值(圖5(b)),定位最終失效.P-EVD算法的輸出結(jié)果顯示其單極子模型與偶極子模型的輸出結(jié)果均僅存在唯一的掃描尖峰,與仿真設(shè)定的聲源類型及方位相同,輸出幅度分別為a_B＝0.97、a_A＝1.048,估計誤差3％和4.8％；從圖中偶極子的掃描結(jié)果還能觀測到輸出偶極子方向為θ＝43.982,與聲源A之間存在2.2％估計誤差.以上說明P-EVD算法可通過掃描結(jié)果判斷聲源類型,實現(xiàn)對聲源空間位置，幅度及方向(偶極子聲源)的滿意估計。

加權(quán)修正參數(shù)的P范數(shù)噪聲源定位性能分析：

仿真結(jié)果顯示出P-EVD算法在不同類型聲源定位識別中的優(yōu)越性，為了進一步討論該算法的穩(wěn)健性，從分析頻率，測量距離與陣列孔徑比及信噪比三方面分析這些參數(shù)對聲源定位誤差及幅度估計誤差的影響。

圖8-10給出了P-EVD聲源定位性能受分析頻率，測距空間比及背景干擾對聲源影響的曲線；通過對比分析可以得到如下結(jié)論：(1)P-EVD算法克服了常規(guī)波束形成低頻受限的缺點，可實現(xiàn)在低，中，高全頻段內(nèi)聲源定位,并不受測量距離及陣列孔徑的約束,定位準確有效；(2)相對于P-EVD算法對聲源方位估計的寬容性，其聲源幅度估計僅在中高頻段內(nèi)有效,且測距孔徑比需小于15方可獲得滿意的幅度估計結(jié)果；(3)P-EVD與CBF的抗干擾能力相當，當背景干擾過強時，兩種方法對聲源方位及幅度的估計都存在巨大的偏差，結(jié)果完全失效，信噪比到0dB以上時才可獲得理想的定位識別結(jié)果。

通過以上仿真結(jié)果來看，P-EVD算法相對與常規(guī)方法對測量參數(shù)的適用性更強，在大部分測量情況下均可獲得滿意的聲源定位識別效果。

以上顯示和描述了本發(fā)明的基本原理和主要特征和本發(fā)明的優(yōu)點。本行業(yè)的技術(shù)人員應(yīng)該了解，本發(fā)明不受上述實施例的限制，上述實施例和說明書中描述的只是說明本發(fā)明的原理，在不脫離本發(fā)明精神和范圍的前提下，本發(fā)明還會有各種變化和改進，這些變化和改進都落入要求保護的本發(fā)明范圍內(nèi)。本發(fā)明要求保護范圍由所附的權(quán)利要求書及其等效物界定。