本發明屬于非線性時間序列分析技術領域，并具體涉及一種高階項電離層延遲對GPS坐標時間序列影響的量化方法。

背景技術：

除了由測站所處板塊構造運動引起的線性趨勢外，GPS坐標時間序列中還呈現顯著的非線性變化，主要表現為季節性的上下波動。這些非線性變化主要包括三種類型：(1)GPS數據處理過程中部分因素未模型化引起的虛假非線性變化，包括高階電離層延遲、未模型化的海洋潮汐分量、S1-S2大氣潮汐等；(2)由地球物理效應引起的測站參考點的真實非線性運動，包括大氣負載、非潮汐海洋負載、水文負載、熱膨脹效應等；(3)觀測噪聲。完善GPS精密數據處理模型、定量確定GPS技術類誤差引起的虛假非線性變化，可以得到更為真實的測站運動趨勢，為監測研究地球系統的長期變化提供真實、可靠的基礎數據。

電離層延遲是GPS定位誤差的主要來源之一，電離層延遲一階項可以通過LC組合觀測值消除。已有的研究成果表明，未考慮二、三階等高階項電離層延遲會造成GPS坐標時間序列中呈現虛假非線性信號，同時也會造成厘米級的衛星位置和地球自轉參數解算偏差(Fritsche等，Geophysical Research Letters，Impact of higher-order ionospheric terms on GPS estimates，2005)。Petrie等學者(Journal of Geophysical Research，Higher-order ionospheric effects on the GPS reference frame and velocities，2010)討論了高階項電離層延遲對于GPS參考框架、速度場的影響，認為忽略高階項會造成約10mm的平移參數變化、0.05ppb的尺度變化以及參考ITRF2005高程方向高達0.34mm/yr的偏移量。上述研究表明，電離層高階項延遲對GPS基準站的影響可達厘米級，所引起的測站位置變化具有區域性的偏移規律和季節性特征，影響量級的大小與衛星軌道的精度、總電子含量、所使用的地磁場模型存在相關性。然而基于長時間跨度的坐標時間序列，高階電離層延遲對測站坐標、季節性信號以及噪聲特性的定量影響還有待研究。

技術實現要素：

針對長時間跨度GPS坐標時間序列，難以定量確定高階項電離層延遲對測站坐標、序列周期性信號、噪聲特性以及坐標參考框架實現的影響，本發明提出了高階項電離層延遲對GPS坐標時間序列影響的量化方法，從而可獲得更為真實的測站非線性運動信號。

為解決上述技術問題，本發明采用如下技術方案：

高階項電離層延遲對GPS坐標時間序列影響的量化方法，包括：

S1收集GPS基準站的原始觀測數據；

S2基于歷史觀測數據進行基線解算，僅考慮電離層延遲一階項，經網平差后將基準統一到ITRF框架下，獲得僅考慮電離層延遲一階項的GPS坐標時間序列，記為序列A；

S3基于歷史觀測數據進行基線解算，考慮電離層延遲的二階項與三階項，計算經電離層高階項改正后的GPS坐標時間序列，記為序列B；

S4將序列A和序列B在時間域對齊后相減，獲得GPS基準站的高階項電離層延遲影響時間序列，記為序列C；

S5對序列A、序列B、序列C分別進行噪聲分析，獲得各序列對應的測站速度、噪聲特性和季節性信息，根據各序列的測站速度、噪聲特性、季節性信息的變化來量化高階項電離層延遲的影響。

步驟S1中所述的GPS基準站具備條件：(1)全球均勻分布；(2)連續觀測時間超過3年；(3)遠離地質活動活躍區域；(4)測站速度精度優于3mm/yr。

步驟S2和S3中，基線解算的數據處理策略均采用如下：

(1)同時解算衛星軌道、地球定向參數、測站坐標、對流層延遲及水平梯度參數；

(2)衛星截止高度角設置為10°；

(3)根據驗后相位殘差對觀測值重新定權；

(4)計算固體潮、海潮、極潮改正，其中海潮負載模型采用FES2004；

(5)使用VMF1投影函數模型和絕對天線相位中心模型。

步驟S3中進行基線解算采用顧及電離層延遲高階項的消電離層組合觀測方程，如下：

式(5)～(6)中，P_c、L_c分別表示組合后的測碼偽距和載波相位的觀測值，n_c、λ_c分別為組合后的整周模糊度和載波波長，ρ為測距碼從衛星至接收機的幾何距離，s、r均為電離層延遲項；f₁和f₂分別表示兩個觀測方程對應的載波頻率。

步驟S5中，采用頻譜分析法或極大似然估計法進行噪聲分析。

步驟S5中，所述的季節性信息包括季節變化引起的周年振幅、周年相位、半周年振幅和半周年相位。

步驟S5中，基于參數模型進行噪聲分析，所述的參數模型如下：

其中，t_p表示坐標序列日解歷元，以年為單位；a為測站位置，b為線性速度；c和d為年周期項系數，分別用來表示周年振幅和相位；e和f為半年周期項系數，分別用來表示半周年振幅和相位；g_j為由于各種原因引起的階躍式坐標突變；T_hj為發生突變的歷元；H為海維西特階梯函數；為觀測噪聲。

與現有技術相比，本發明具有如下特點：

(1)顧及二、三階電離層延遲，得到高階項電離層延遲引起的GPS基準站虛假非線性位移坐標時間序列。

(2)可定量確定高階電離層延遲對測站坐標時間序列、最優噪聲模型以及坐標參考框架實現的具體影響。

(3)削弱由GPS技術類誤差或數據處理模型不完善引起的測站虛假非線性變化，最終得到更為真實的測站非線性位移時間序列，有助于進一步揭示GPS坐標時間序列季節性信號的物理機制，為建立估計基準站非線性變化的地球參考框架提供支持與借鑒。

附圖說明

圖1為本發明的具體流程圖；

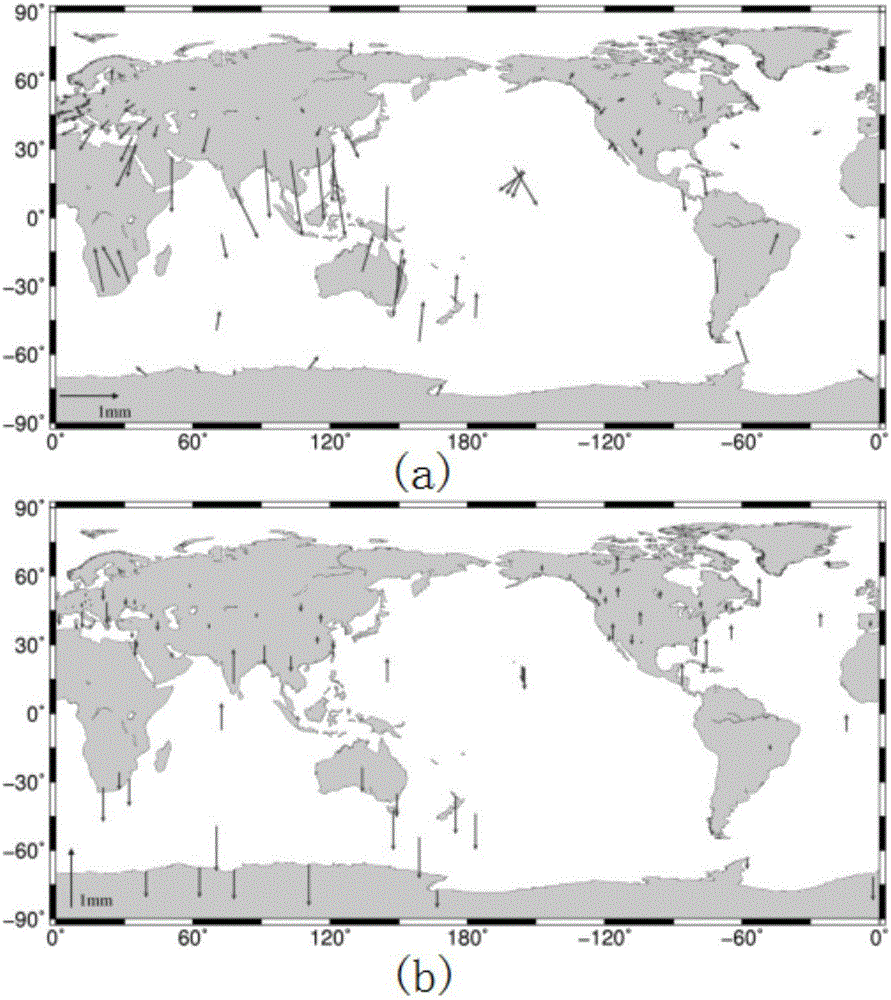
圖2為實施例中計算得到的全球GNSS基準站由高階項電離層延遲引起的坐標變化圖，其中，圖(a)為水平方向坐標變化，圖(b)為垂直方向坐標變化；

圖3為實施例中高階項電離層延遲改正前后的全球GNSS基準站堆積頻譜變化圖，其中，圖(a)為N方向的堆積頻譜變化圖，圖(b)為E方向的堆積頻譜變化圖，圖(c)為U方向的堆積頻譜變化圖；

圖4為實施例中高階項電離層延遲改正前后的周年、半周年振幅變化圖，其中，(a)～(c)分別是N方向、E方向、U方向的周年幅度變化圖；(d)～(f)分別是N方向、E方向、U方向的半周年幅度變化圖；

圖5為實施例中高階項電離層延遲改正前后的噪聲振幅變化圖，其中，(a)～(c)分別是N方向、E方向、U方向的噪聲幅度變化圖；(d)～(f)分別是N方向、E方向、U方向的噪聲幅度變化圖；

圖6為實施例中計算得到的由高階項電離層延遲引起的基準轉換參數變化圖，其中，圖(a)～(d)分別為原點平移參數T_X、T_Y、T_Z、尺度隨時間的變化圖，T_X、T_Y、T_Z分別表示原點在X、Y、Z坐標軸下的平移參數。

具體實施方式

下面結合附圖和具體實施方式對本發明技術方案做進一步說明。

本實施例是計算104個全球分布的IGS(International GNSS Service)基準站的高階電離層延遲影響，具體步驟參見圖1，包括：

步驟1，根據研究目的，選取待研究的GPS基準站，并收集GPS基準站的原始觀測數據。

本實施例中，選取全球均勻分布的104個IGS基準站，采集了該104個IGS基準站從1999年到2003年太陽活動高峰期的5年觀測數據。

步驟2，基于原始觀測數據進行基線解算，僅考慮電離層延遲一階項，獲得GPS基準站的坐標時間序列(即GPS坐標時間序列)，記為序列A。

基線解算采用GAMIT軟件，選取每周三作為周解的平均值，數據處理策略按照步驟2的過程進行，同時解算衛星軌道、地球定向參數、測站坐標、對流層延遲及水平梯度參數，衛星截止高度角設置為10°，使用VMF1投影函數模型和絕對天線相位中心模型，并計算固體潮、海潮、極潮改正，其中海潮負載模型采用FES2004。

步驟3，基于原始觀測數據進行基線解算，考慮電離層延遲的二階項與三階項，計算經電離層高階項改正后的GPS坐標時間序列，記為序列B。

經電離層高階項改正后的GPS基準站坐標時間序列采用如下方法獲得：

考慮載波相位測量原理及GPS信號的雙頻特征，顧及電離層延遲高階項的觀測方程為：

式(1)～(2)中，i表示第i個觀測方程；P_i、L_i分別表示第i個觀測方程的測碼偽距和載波相位的觀測值，f_i表示第i個觀測方程的載波頻率，ρ為測距碼從衛星至接收機的幾何距離；n_i表示第i個觀測方程的整周模糊度，λ_i表示第i個觀測方程的相位載波波長。

電離層延遲項q、s、r分別為：

式(3)中，c代表真空光速；θ_B代表地磁偏角；s表示傳播路徑；為地磁場強度；Ne為電子密度；為GPS信號傳播路徑上的單位向量；形態系數η為常數0.66，N_max表示信號傳播路徑上的最大電子密度，計算公式為：

式(4)中，TEC為電離層電子密度。

由公式(1)～(3)得到顧及電離層延遲高階項的消電離層組合觀測方程：

式(5)～(6)中，P_c、L_c分別表示組合后的測碼偽距和載波相位的觀測值，n_c、λ_c分別為組合后的整周模糊度和載波波長。

采用顧及電離層延遲高階項的消電離層組合觀測方程計算經電離層高階項改正后的GPS坐標時間序列。

步驟4，將序列A和序列B在時間域對齊后相減，獲得對應GPS基準站的高階項電離層延遲影響時間序列，記為序列C。

步驟5，對序列A、序列B、序列C分別進行噪聲分析，獲得各序列對應的測站速度、噪聲特性和季節性信息，根據序列的測站速度、噪聲特性、季節性信息的變化量化高階項電離層延遲的影響。

噪聲分析可采用頻譜分析法或極大似然估計法(Maximum Likelyhood Estimation，MLE)等分析噪聲特性。MLE可以同時估計噪聲類型、周期性振幅、測站速度及不確定度，并且可避開頻譜分析的局限性，因此被認為是目前最準確的噪聲分析方法。

下面將以極大似然估計法為例，詳細說明本步驟的噪聲分析過程：

對日解坐標分量時間序列建立下列參數模型：

式(7)中，t_p表示坐標序列中第p個歷元對應的時間，以年為單位；y(t_p)表示歷元t_p下的測站坐標；a為測站位置，b為線性速度，c和d為年周期項系數，e和f為半年周期項系數；n_j代表突變發生次數，g_j為由于各種原因引起的第j次階躍式坐標突變；T_hj為發生突變的歷元；H為海維西特階梯函數(Heaviside step function)，發生突變前H值為0，發生突變后H值為1；為觀測噪聲，假設由振幅分別為a_w和b_κ的白噪聲及冪律譜噪聲組成，則有：

式(8)中，α(t_p)和β(t_p)分別為白噪聲和冪律譜噪聲的分量。

觀測值協方差陣C可表示為：

式(9)中，I為單位陣；J_κ對應譜指數為κ的冪律譜噪聲協方差陣：

J_κ＝TT^T (10)

轉換矩陣T的表達式為：

式(11)中，N為轉換矩陣T的維度；n＞0；當n＝0時，

協方差矩陣C可以表示不同形式的隨機噪聲過程，例如白噪聲、閃爍噪聲、隨機游走噪聲、一階高斯-馬爾科夫噪聲及其相應的組合等。

上述，a、b、c、d、e、f、g_j及噪聲分量振幅a_w、b_κ為待求參數。由于隨機模型未知，無法采用最小二乘求解模型參數，于是按照極大似然估計準則同時確定上述待求參數，即選擇不同的噪聲模型，確定各噪聲分量的大小，使得坐標時間序列的殘差與其觀測值協方差陣C的聯合概率密度值達到最大：

等價于聯合概率函數值的對數達到最大：

不同的模型組合將得到不同的極大似然估值，選擇聯合概率密度值最大的模型(即公式(7))作為最優噪聲模型。蒙特卡羅模擬實驗表明：95％的顯著水平下，當兩種噪聲模型的MLE之差大于3.0時，兩種模型具有可區分性。

本步驟即通過噪聲分析確定最優的參數模型(見公式(7))，根據參數模型中可獲得噪聲特征，根據參數模型中c、d、e、f可獲得季節信息，c和d分別表示周年振幅和相位，e和f分別表示半周年振幅和相位。

本實施例中，采用MLE分析噪聲特性，利用上述步驟估計最優噪聲模型組合及相應噪聲的振幅。不同的噪聲類型包括白噪聲、有色噪聲(包括冪律噪聲、隨機游走噪聲、高斯馬爾科夫噪聲等)以及他們之間的任意組合。

本步驟中，季節性變化分析基于估計坐標時間序列得到的周年振幅、周年相位、半周年振幅、半周年相位等信息，分別比較基于序列A、B得到的不同參數的變化來分析高階電離層效應對季節性變化的影響。

實施例

采用本發明方法定量確定104個全球分布的IGS基準站高階電離層延遲的影響時間序列，并分析了加入高階電離層改正前后GPS坐標時間序列周期特性、噪聲特性的差異，最后量化了其對坐標參考框架實現的影響。

首先，定量給出了電離層延遲高階項對IGS基準站坐標的影響，見圖2。分析結果表明，平面方向來說，高緯度測站有著向北偏的趨勢，而赤道區域測站則向南移，且赤道附近的偏移值大于其他緯度地區；從高程前后變化角度分析，北半球大多數測站高程增加，而南半球大多數測站高程則減小；我國境內中緯度IGS站均有向南偏移現象，且向南偏移變化相對穩定在正南方向，東西方向則變化較小。

其次，對高階項改正前后的基準站坐標時間序列進行了頻譜分析，見圖3。整體上，高階項延遲后N方向的功率譜值減小，表明高階項延遲后坐標時間序列的N方向的周期信號振幅降低；高階項延遲改正后E方向的功率譜特征由一連串無規律波動變為與N、E方向相一致的變化趨勢，表明高階項延遲后，E方向整體變化趨勢更為一致，由高階項誤差引起的波動顯著減小；對U方向，從整體功率譜值和主要周期來說，高階項延遲對于U方向的影響與N方向較為一致，改正后功率譜減小。圖4為定量計算的周期振幅變化，結果表明，電離層高階項延遲改正后，均有超過一半數目的測站三個坐標分量的周年和半周年振幅降低，且半周年振幅減小的測站數目多于周年振幅減小的測站數目。

然后，對高階項改正前后的基準站坐標時間進行了噪聲分析，見圖5。不論是僅考慮電離層一階項改正，還是顧及高階項延遲改正，坐標時間序列在N、E方向的噪聲水平明顯低于U方向(一般在2～3倍水平)。高階項電離層改正后，大部分測站的白噪聲和閃爍噪聲振幅均有所降低，且白噪聲較閃爍噪聲振幅的降低更為顯著。就基準站噪聲減小的測站數目而言，N方向的閃爍噪聲振幅減小最為顯著，減小的測站比例達67.5％。相較于閃爍噪聲，白噪聲在三個分量噪聲振幅減小效果更為顯著，分別有61.4％,71.6％和81.8％的測站在N、E、U三個分量白噪聲振幅減小。就減小的噪聲振幅而言，高階項延遲最大可以解釋N、E、U三個分量44.02％(NICO)、91.10％(NOT1)、49.8％(NICO)的白噪聲振幅，最多可解釋67.63％、53.59％、71.30％的閃爍噪聲振幅(均出現在ANKR站)。噪聲振幅有顯著減小的測站大多位于中低緯度區域。

此外，還分析了模型化高階項改正對于基準轉換參數的影響，見圖6。結果表明，電離層延遲高階項改正會影響參考框架的原點和尺度，尤其是原點Z方向的平移，可達30mm，X、Y方向的平移所受的影響相對較小，大部分維持在5mm以下。對于尺度參數基本維持在0.2ppb以下。此外，基準轉換參數的變化與電離層總電子含量值在此期間的變化具有很好的一致性。

本文中所描述的具體實施例僅僅是對本發明精神作舉例說明。本發明所屬領域的技術人員可以對所描述的具體實施例替換成其他區域，做各種各樣的修改或補充，或采用相似方式替代，但并不會偏離本發明的精神或者超越所附權利要求書所定義的范圍。