本發明屬于衛星導航領域，是衛星導航航海應用中一種大圓航線航路點劃分與航程計算方法。

背景技術：

隨著信息技術、衛星導航技術的發展，海用衛星導航設備的技術越來越復雜，功能越來越完善，智能化水平也在不斷提高。當前，海用衛星導航設備除了計算和顯示定位信息以外，具備導航和航路規劃功能也成為海用衛星導航接收設備的重要指標之一。精確良好的航路規劃和計算功能，能夠為遠距離航行的船舶提供最優路徑，節省航行時間、提高經濟效益。

大圓航行是指航線為一個圓，其原點在地心，大圓航線是跨洋航行時的最短航程航線，將地球當作圓球體時，地面上兩點間的距離以連接兩點的小于180°的大圓弧弧長為最短。所以理論上如果能將船舶始終保持在該圓弧之上，則沿大圓弧航行，航程為最短。但由于大圓弧與各子午線交角都不相等(沿赤道和子午線航行除外)，船舶要想沿大圓航行，駕駛員就必須不停地設法確定當時船舶應執行的大圓航向，這在實際操作中是不可能的。所以以往所謂的大圓航線航行，并不是船舶不斷變向、嚴格地沿大圓弧航行，而是對大圓航線進行分段近似，實際海上航行時為了便于操縱船只一般分段采用恒向線航線，即航向在該分段內保持不變，恒向線在墨卡托海圖上表現為直線，但實際在地球表面上一般為球面螺旋曲線。

目前，在海用衛星導航設備大圓航線航路點劃分與航程計算領域，國內對于該領域缺乏從大圓航線航路點劃分到航程計算的有效方法，所以，作為海用衛星導航接收設備關鍵技術，其對船舶海上航行導航具有重要的意義。

技術實現要素：

為了克服現有技術的不足，本發明提供一種海用衛星導航設備大圓航線計算方法，能夠快速精確的計算大圓航線等航程、等經度差劃分出的各航路點經緯度、航程、航向以及大圓航線總航程。

本發明解決其技術問題所采用的技術方案包括以下步驟：

(1)根據大圓航線的起始點經緯度和到達點經緯度計算大圓航線弧長和初始航向D_λ為起始點和到達點的經度差；

(2)在大圓航線上按照等航程δ或等經度Δλ差劃分航路點i＝1,2,3…，等航程劃分的航路點中，緯度經度λ_i＝λ₁+A_i，其中，A_i為起始點與航路點D_i的經度差；等經度劃分的航路點中，緯度經度λ_i＝λ₁+Δλ(i-1)，其中，為大圓航線頂點的緯度，λ_V為大圓航線頂點的經度；

(3)計算任意緯線到赤道的子午線弧長和任意兩條緯線的緯度漸長率差D_MP＝MP₂-MP₁，其中，a為地球橢圓體長半軸，e為地球橢圓體偏心率，緯線的緯度漸長率

(4)計算各航路點之間的航向和航程其中，和D_λ為相鄰航路點間的緯差和經差；

(5)經過累加運算得到大圓航線的總航程N為大圓航線上航路點數量。

本發明的有益效果是：能夠快速精確的計算大圓航線等航程、等經度差劃分出的各航路點的經緯度、航程、航向以及大圓航線總航程信息。

附圖說明

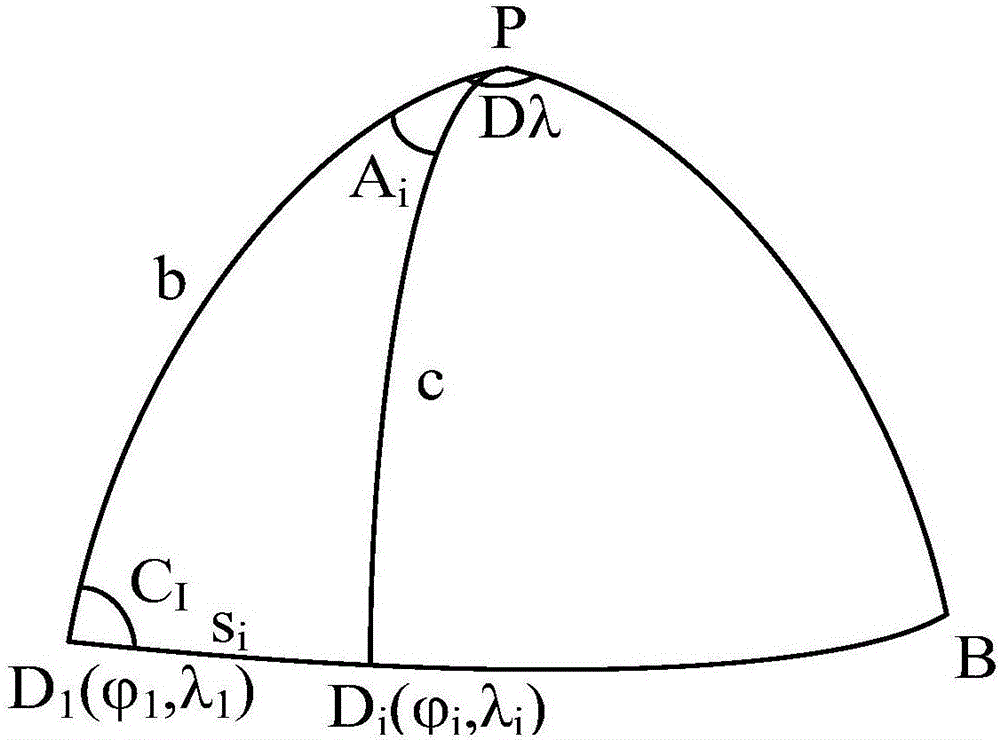
圖1是大圓航線求解示意圖；

圖2是航路點航程、航向計算示意圖；

圖3是大圓航線弧長、起始航向計算示意圖；

圖4是大圓航線和各分航路點示意圖；

圖5是子午圈示意圖；

圖6是墨卡托航法示意圖。

具體實施方式

下面結合附圖和實施例對本發明進一步說明，本發明包括但不僅限于下述實施例。

本發明在已知大圓航線起始位置和結束位置經緯度的情況下，通過設置大圓航線上各航路點，或者按照等航程、等經度差方法劃分出航路點再計算出大圓航線各個航路點的經緯度；大圓航線上航路點確定后，就可以計算出航路點之間的航向、航程，最后累加得到大圓航線的總航程。該方法基于兩個假設：1、大圓航線上各航路點已設置或者按照等航程差、等經度差生成；2、大圓航線上各個航路點之間按照恒向線航行。

本發明包括如下步驟：

步驟一：計算大圓航線的弧長和起始航向；

步驟二：計算大圓航線上等航程或等經度差劃分航路點；

步驟三：計算子午線弧長和緯度漸長率差；

步驟四：計算航路點間恒向線航程、航向；

步驟五：計算大圓航線總航程。

所述步驟一具體為：首先設置大圓航線起始點和到達點，主要包括起始點和到達點的經緯度位置；根據大圓航線的起始點和到達點計算出大圓航線的弧長和初始航向信息。

所述步驟二具體為：在大圓航線上按照等航程或者等經度差的方法劃分航路點，根據各航路點與大圓航線的關系，求解球面三角函數，解出各個航路點的經緯度位置信息。

所述步驟四具體為：依據各個航路點的經緯度位置信息，采用恒向線計算方法，計算出航路點之間的航向和航程信息。

大圓航線的航程為大圓的弧長，為兩點之間在球面上的最短距離，但是大圓航線的航向并非一個固定值，而是一個變化的值，在實際航海導航中，很難做到航向不斷的隨大圓航線而，因此大圓航線上各個航路點之間的航線航程使用恒向線方法計算，雖然不是球面上最短距離，但是可以保證兩個航點之間航向為一個固定值。

假設大圓航線如圖1所示，大圓航線起始點為到達點為兩點經緯度均已知，且設定北緯、東經為正值，南緯、西經為負值。

其中(i＝1,2,3…)為大圓航線上的某一個分段航路點，A_i為起始點與航路點D_i的經差，S_i為起始點至D_i的弧長，P為極點，假設以等航程δ或者等經度差Δλ劃分大圓航線生成各航路點，則通過求解球面三角形可以得到大圓航線的弧長、初始航向以及大圓航線上等航程、等經度差產生的各個航路點的經緯度位置，其計算表達式分別為：

大圓航線弧長計算表達式：

初始航向計算表達式為：

假設以等航程δ或者等經度差Δλ劃分大圓航線生成各航路點，則通過求解球面三角形函數可以得到大圓航線上等航程、等經度差產生的各個航路點的經緯度位置。

等航程差劃分大圓航線時，大圓航線上任一航路點(不包括起始點和到達點)(i＝1,2,3…)緯度計算表達式為：

經度計算表達式為：

λ_i＝λ₁+A_i i為整數且1＜i＜N (4)

其中λ₁為大圓航線起始航路點的經度，A_i為大圓航線起始點與某一航路點D_i的經度差。

等經度差劃分大圓航線時，大圓航線上任一航路點(不包括起始點和到達點)(i＝1,2,3…)緯度計算表達式為：

其中為大圓航線頂點的緯度，λ_V為大圓航線頂點的經度。

經度計算表達式為：

λ_i＝λ₁+Δλ(i-1) i為整數且1＜i＜N (6)

其中λ₁為大圓航線起始航路點的經度，Δλ為等經度差劃分大圓航線的劃分間隔。

航海導航實際使用中，大圓航線航程最短，但是其航向不斷發生變化，因此一般對大圓航線使用航路點進行分段近似，航路點之間的航程按照恒向線方法航行和計算，可保證航向角在該段航程中固定不變。

如圖2，β為緯度，γ為經度，A為航向角，OB和CD為兩條平行圈，OD和BC為兩條子午線。計算橢球面微分三角形OBC，求解恒向線微分方程可解出航路點間航程OC和航向角A。

計算航路點之間恒向線航程之前需要首先計算子午線弧長L和緯度漸長率差D_MP，利用L和D_MP可依次計算出各航路點之間的航向C_i和航程S_i，經過累加運算可得到大圓航線的總航程S_D。

本發明的實施例包括以下步驟：

步驟一：計算大圓航線的弧長和起始航向：

已知大圓航線起始點為到達點為如圖3，兩點經緯度均已知。

計算球面三角形P_NAB則大圓航線弧長S的計算表達式為：

其中D_λ為起始點至到達點經度差，計算表達式為：

D_λ＝|λ₁-λ₂| (8)

同時可得大圓航線起始航向C₁的計算表達式為：

由于經緯度均有名稱和符號，在利用以上公式求取航向和航程時可使用以下規律：

1、起始點緯度，無論南北一律取正值，到達點緯度與起始點緯度同名時取正值，與起始點緯度異名時取負值。

2、其中Dλ為起點和終點的經度差，經度差不論東或西一律取正值。

3、若按照上述公式計算的cos(S)為正值，則航程S為小于5400n mile(90°)的值；若cos(S)為負值，則航程S為大于5400n mile(90°)的值。

4、按照上述取值，求取始航向時，求得的航向為用半圓周法表示的值(0°～180°)，其命名的第一個字母與起始點緯度同名，第二個字母與經差同名。如果求得的函數值為負，則航向取大于90°小于180°的值，(即如果COSC_I為負值，直接球反三角函數即可；如果tanC_I為負值，則求出的C_I為負值，應加上180°換算為大于90°小于180°的值)。最后將用半圓周發表示的航向換算為用圓周法表示的即可。

步驟二：計算大圓航線上等航程或等經度差劃分航路點

1、等航程劃分航路點

大圓航線與各航路點的關系如圖4所示，假設弧AD為一條大圓航線，線段AB、BC、CD將大圓航線的弧長分段進行了內接法近似，AB、BC、CD之間按照恒向線航行航向固定。

其中A、B、C、D為大圓航線上劃分出來的航路點。航路點的劃分一般按照實際航海需要劃分，也可以按照等航程或等經度差等方法劃分，方法如下：

1、等航程劃分航路點

假定設置的等航程間距為δ，大圓航線弧長為S，則可得大圓航線航路點數量N的計算表達式為：

即為，大圓航線弧長S與等間隔航程δ相除后，向上取整得到的值N。

等航程劃分后的航路點經緯度的計算如圖1中，分別為大圓航線的起始點與到達點，其經緯度均已知，且北緯、東經取正值，南緯、西經取負值。(i為整數且1＜i＜N)為劃分出的大圓航線上的某一航路點。A_i為起始點與航路點D_i的經差，S_i為起始點至航路點Di的弧長，等航程劃分大圓航線時有S_i＝δ，P為極點，則在球面三角形PD_iD₁可得為：

所以可得分航路點的緯度的計算表達式為：

計算球面三角形可得

所以，可得大圓航線起始點與航路點D_i的經度差計算表達式為：

于是可得大圓航線分航路點的經度λ_i的計算表達式為：

λ_i＝λ₁+A_i (15)

其中λ₁為大圓航線起始航路點的經度，A_i為大圓航線起始點與某一航路點D_i的經度差。

2、等經度差劃分航路點

假設設置的劃分大圓航線的等經度差的為Δλ，則在已知大圓航線弧長S和航向CI的情況下，可得大圓航線上航路點數量N的計算表達式為：

其中D_λ為大圓航線起始點和到達點的經度差，計算方法見式(8)。

等經度差劃分后的航路點經緯度計算方法如圖2中，分別為大圓C航線的起始點與到達點，它們的經緯度均已知，且北緯、東經取正值，南緯、西經取負值。假設由步驟一已計算得到大圓航線的弧長為S，初始航向為C_I；大圓航線的起始點緯度根據南北緯取值，北緯為正，南緯為負；到達點的緯度若與同名，取正值，異名則取負值。

計算大圓航線初始航向的半圓航向，計算表達式如下：

大圓航線頂點是大圓航線上緯度達到的最高點(大圓航線上緯度值最大的點)，在該點大圓弧與子午線相交成直角，大圓航向為90°或270°。大圓航線頂點坐標可按以下公式求取：

其中，D_λV為起始點至大圓航線頂點的經差，為大圓航線頂點的緯度，λ_V為大圓航線頂點的經度。

因此，大圓航線各分航路點按照等經度劃分，各航路點的經度λ_i的計算公式為：

λ_i＝λ₁+Δλ(i-1) i為整數且1＜i＜N (19)

其中N為大圓航線上等經度差劃分出的航路點數量計算方法見公式(13),通過求解球面三角形可知：

進一步可得，各航路點緯度的計算表達式為：

步驟三：計算子午線弧長和緯度漸長率差

在較為準確的航海計算中，應將大地球體當作兩極略扁的地球橢圓體，才能得出有足夠精度的結果。地球旋轉橢圓體的旋轉橢圓，即子午圈，如圖5所示：其中，為地理緯度(橢圓子午線上某點的法線與赤道面的交角)；a為地球橢圓體長半軸；b為地球橢圓體短半軸；r為某地(A點)所在緯度的等緯圈半徑，按下式計算

A點的橢圓子午線的曲率半徑M為

式(22)和式(23)中：e為地球橢圓體偏心率。參數a和e在不同的大地坐標系中取值不同，計算時應根據所使用海圖的坐標系進行選取，如常用的WGS84坐標系中a＝6 378 137m,e＝0.081 819 190 842 621 5。從任意一條緯線到赤道的子午線弧長，用L表示，則有

對式(24)積分可得：

按照泰勒級數展開積分式中的函數再積分，并以海里為單位，便可得到任意緯線到赤道的子午線弧長L的計算表達式為：

其中：

則任意兩條緯線和之間的子午線弧長D_L計算表達式為：

D_L＝L₂-L₁ (30)

如將L投影到墨卡托海圖上，根據墨卡托等角正圓柱投影原理，可得該緯度的緯度漸長率MP的計算表達式為：

將自然對數函數改以雙曲函數表示，并以1′(1分)經度長度作為單位的長度。

因為a＝1經度分Parc1′＝180×60Pπ＝10 800Pπ，則

任意兩緯線在墨卡托海圖上的距離即緯度漸長率差D_MP計算表達式為：

D_MP＝MP₂-MP₁ (33)

步驟四：計算航路點間恒向線航程、航向

假設航路點A經緯度和航路點B經緯度在計算兩點之間的恒向線航向和航程中，首先要計算兩點間的緯差和經差D_λ，其計算公式為

計算時將北緯取為正值(+)、南緯取為負值(-)；東經取為正值(+)、西經取為負值(-)；求其代數和。緯差的范圍為-90°～+90°；經差D_λ的范圍為-180°～+180°，當(λ₂-λ₁)>180°時

D_λ＝-360°+λ₂-λ₁ (35)

當(λ₂-λ₁)<-180°時

D_λ＝360°+λ₂-λ₁ (36)

1、當緯度差時航向和航程的計算

當緯差時，表明航線位于等緯度圈上。如兩點間經差D_λ>0，則恒向線航向為正東,即C＝90°；如D_λ<0，則恒向線航向為正西，C＝270°，即

C＝[2-sgn(D_λ)]·90° (37)

其中：sgn(·)為取符號值。此時,恒向線航程S即為兩點間的等緯圈弧長，并統一到以法定海里值為單位，有

2、當經差D_λ＝0時恒向線航向和航程的計算模型

當經差D_λ＝0時，表明船舶沿子午線航行。如兩點間緯差則恒向線航向為正北，即C＝0°；如則恒向線航向為正南，C＝180°，即

此時,兩點間的恒向線航程S，在簡單的航海計算中按地球圓球體計算，在精確計算時,應按地球橢圓體計算，即

S＝|D_λ| (40)

3、當D_λ≠0時，恒向線航向和航程的計算模型

當D_λ≠0時，恒向線航線在地球橢圓體表面上表現為一條球面螺旋曲線。為了解決此時恒向線航向的計算問題,將恒向線投影到墨卡托海圖上。設船舶從起航點A航行至到達點B，投影到墨卡托海圖上，分別為A′和B′，恒向線直線A′B′與對應的經線和緯線構成一個直角三角形，如圖6所示。

ΔΑ′B′C′表示緯度漸長率DMP、經差D_λ和恒向線航向C的關系，顯然有

由于arctan(Dλ/DMP)的范圍為-90°～+90°，而圓周法航向C的范圍為0°～360°，因此，航向計算公式為

恒向線航程S表現為線段長度由等角投影可得航程S的計算表達式為：

其中D_L為子午線弧長，計算方法見式(26)。

步驟五：計算大圓航線總航程

大圓航線的總航程為航路點間分段航程的累加。假設大圓航線上航路點數量為N，航路點為(i為整數且1≤i≤N)，其中為各航路點緯度，λ_i為各航路點經度。假設利用式(38)、(40)、(44)計算得到航路點D_i和D_i+1之間的航程為S_i(1≤i≤N-1)，則大圓航線總航程S_D的計算表達式為：