本發明屬于遙感圖像處理技術領域，具體涉及一種基于幀間連續性的無人機多幀圖像目標定位校正方法。

背景技術：

隨著電子信息技術的不斷發展，無人機在軍用和民用等領域逐漸得到了廣泛的應用。其中，重要一項就是利用無人機對地進行目標定位。然而，在多數情況下，由于一些客觀方面的限值，比如安裝誤差、測量單元精度較低等原因，無人機的各個姿態信息往往含有一定的誤差，導致目標定位精度不高，加之無人機的拍攝姿態的自由性，往往使得得到的航拍圖像有一定的畸變。這不僅影響到直觀上對探測區域的認知，也對后續相關圖像處理等方面的操作造成了極大的影響。此外，無人機對地目標定位技術則是聯系圖像與實際空間位置的手段，無人機的許多飛行任務，如跟蹤、監視等都是建立在無人機對地目標定位的基礎上的。無人機對地目標定位精度直接限制了無人機的偵查、探測等一系列工作的精準度。因此，很有必要對如何提高無人機對地目標定位精準度展開研究。

現有的無人機對地目標定位方法主要都是基于成像原理的定位模型。基于成像原理的定位模型，利用針孔成像原理，通過多個旋轉矩陣建立圖像像素坐標與大地坐標之間關系，從而實現目標定位。參考文件1[何喬,趙泳,張保明,等.基于廣義點的相對定向和絕對定向[j].海洋測繪,2006,26(4)]公開了一種基本的目標定位方法，該方法據共面條件利用解析法相對定向和絕對定向兩步得到目標的空間位置信息。其中建立被攝物體的近似幾何模型的過程被稱為相對定向。將模型坐標轉換為地面坐標，該過程稱為絕對定向。然而，由于受到無人機位姿信息等輸入數據的精準度限制，目標定位精準度較低。而且，如圖1所示，對于無人機航拍過程中相鄰幀具有重疊性的特點，以上方法沒有很好的利用這一特性。

為了提高對地目標定位精準度，可以對目標定位過程中的誤差進行分析并建立誤差的預測補償模型，從而對誤差進行補償，達到提高對地目標定位準確度的目的。另一方面，可利用無人機航拍圖像高重疊率的特點，對多幀航拍圖像進行分析，通過對多幀航拍圖像公共點之間的相應關系以及系統誤差的分布特征等方面入手，達到提高定位精準度的目標。

技術實現要素：

針對滿足幀間重疊率要求的連續幀航拍圖像，本發明充分利用無人機提供的遙測參數，根據共同點在連續幀圖像中對應的兩條同名光線滿足共面條件建立約束條件，將相對—絕對定位法與無人機遙測信息進行結合，實現對姿態信息誤差的補償，從而達到提高目標定位準確度的目的。

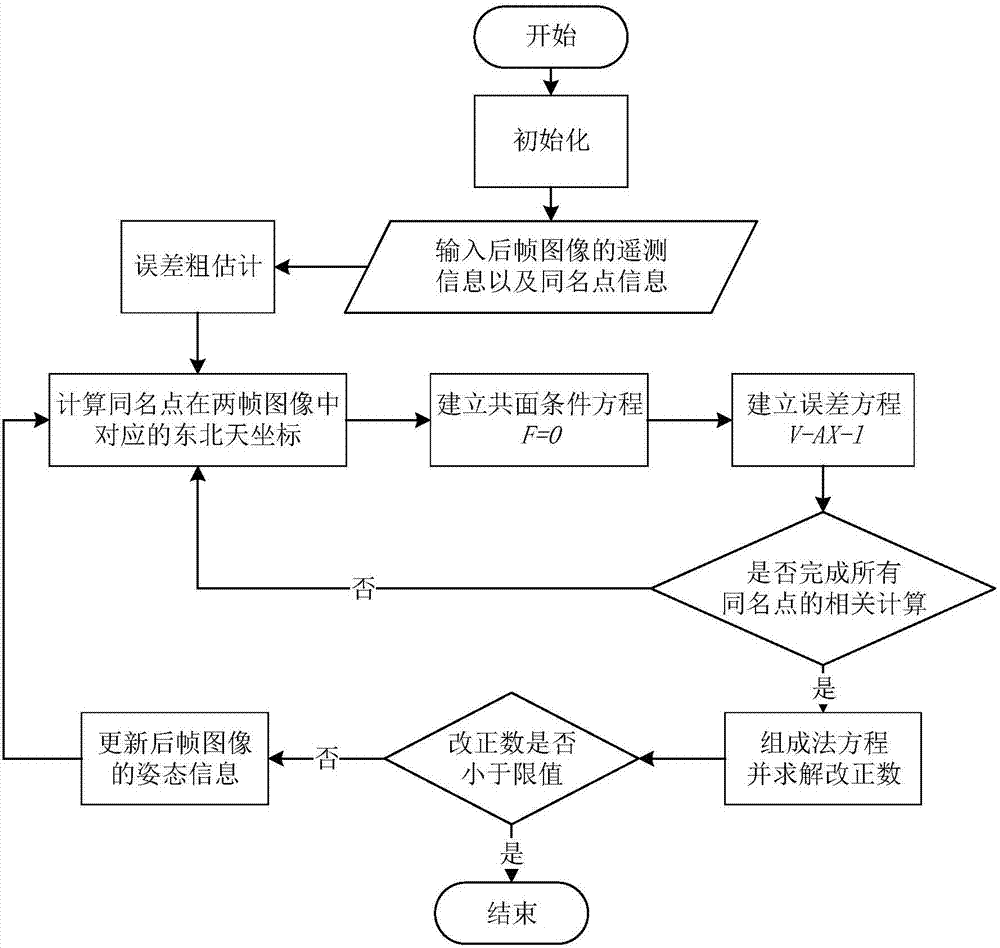
為了達到上述目的，本發明提出了一種基于幀間連續性的無人機多幀圖像目標定位校正方法，實現步驟包括：

計算相鄰幀圖像的重疊率，所述重疊率是指在兩幀圖像的重疊區域中的同名點數量；

當重疊率大于設定的最低門限值時，執行下面過程(1)～(4)：

(1)先利用上一幀圖像的姿態信息的改正數對當前幀圖像的姿態信息進行粗校正，作為當前幀圖像的姿態信息的近似值；

(2)將同名點在在當前幀圖像和上一幀圖像中的像素坐標轉換為在各自東北天坐標系下的坐標，所述的東北天坐標系以各個航拍位置為原點；根據兩個同名光線在同一平面的共面條件建立f方程；

無人機拍攝當前幀圖像時攝像機光學中心在東北天坐標系下的坐標為[xs2ys2zs2]，拍攝上一幀圖像時攝像機光學中心在東北天坐標系下的坐標為[xs1ys1zs1]，則攝像機光學中心的位移矢量[bxbybz]＝[xs2ys2zs2]-[xs1ys1zs1]；

設同名點在當前幀圖像中的像素坐標轉換為東北天坐標系下的坐標為[xn1yn1zn1]^τ，同名點在上一幀圖像中像素坐標轉換為東北天坐標系下的坐標為[xn2yn2zn2]^τ；

建立的f方程表示為：

(3)遍歷所有同名點，對各同名點執行(2)，求解各個姿態的改正數；

(4)將得到的各姿態的改正數加到各姿態的近似值上，更新當前幀圖像的姿態信息的近似值；判斷得到的改正數是否低于設定的限值，若是，停止迭代，輸出當前幀圖像的姿態信息的改正數以及近似值；否則，繼續利用新的近似值繼續執行(2)。

所述基于幀間連續性的無人機多幀圖像目標定位校正方法，選擇一幀有已知地面控制點的航拍圖像為起始圖像，通過單幀圖像的定位反向校正獲取該航拍圖像對應的姿態信息改正數，姿態信息包括：無人機的經緯高信息對應的大地坐標，平臺高低角，平臺方位角，飛機俯仰角，飛機橫滾角，飛機航向角。

所述基于幀間連續性的無人機多幀圖像目標定位校正方法，利用當前幀圖像的姿態信息的近似值來確定f的初始值f0。

所述基于幀間連續性的無人機多幀圖像目標定位校正方法，建立f的誤差方程，通過遍歷所有同名點，建立法方程求解得到各個姿態的改正數。

本發明具有如下的優點：

(1)本方法能夠充分利用連續幀間高重疊性且姿態變化連續的特點，將具有地面控制點的首幅圖像的精準度維持到具有重疊區域的后續圖像，使得后續不包含地面控制點的圖像依然能夠擁有較高的定位精準度。

(2)本方法根據各個坐標之間的變換關系和矢量的運算性質，利用無人機提供的遙測數據與共面條件相結合，將幾何模型的確定與地理位置的計算整合到一步完成。

(3)本方法中的粗校正的初始化策略減少了迭代次數，同時也避免了最終結果陷入局部最優的情況。

(4)現有的基于共面條件的兩步定位算法在計算過程中需要通過假設角元素為小值，因此該方法僅僅局限于小角度下，而本方法沒有此限制。

(5)本方法通過粗校正減少迭代次數，通過f方程整合幾何模型的確定與地理位置的計算減少計算量，從而實現數據計算的實時性，因此可應用于在線航拍過程中，實時性地修正后幀圖像參數從而提高定位結果的精準度。

附圖說明

圖1是無人機航拍圖像幀間連續性的示意圖；

圖2是本發明基于共面條件的幀間校正定位方法的流程圖；

圖3是本發明幀間校正過程中姿態誤差粗估計流程圖；

圖4是各幀圖像對應的東北天坐標系間關系示意圖；

圖5是斜視角增大時本發明提出的目標定位方法與基本目標定位的誤差比較。

具體實施方式

下面結合附圖，對本發明的具體實施方法作進一步的詳細說明。

本發明提供的基于幀間連續性的無人機多幀圖像目標定位方法，流程如圖2所示，包括以下幾個步驟：

第一步，起始圖像初始化。

選擇一幀有已知地面控制點的航拍圖像為起始圖像，通過單幀圖像的定位反向校正獲取該航拍圖像對應的姿態信息改正數，得到準確的姿態信息。

具體為：

(1)根據遙測參數計算旋轉矩陣

其中，是平臺高低角，γ是平臺方位角，ω是飛機橫滾角，φ是飛機俯仰角，κ是飛機航向角。形如ra(b)的矩陣表示b關于東北天坐標系的a軸的旋轉矩陣。計算r的目的是為了求得圖像中像素坐標與東北天坐標的轉換關系。

(2)根據共線條件方程計算地面控制點在無人機的攝像機平臺坐標系的近似值(x)(y)。

設地面控制點對應的大地坐標為(x,y,z)，無人機的經緯高信息對應的大地坐標為(xs,ys,zs)，相機焦距為f。地面控制點對應在攝像平臺坐標系下的像素坐標為(x,y)，該圖像像素坐標(x,y)在東北天坐標系對應的坐標為(u,v,w)。

根據共線方程有：其中，λ是比例因子。

則寫成矩陣形式為：

由于r為正交矩陣，則r^τ＝r^-1，從而得到關系：

進而得到中心投影的構像方程，又稱共線條件方程：

利用無人機的遙測參數作為初始值，帶入共線條件方程得到控制點像點坐標的近似值(x)、(y)。

(3)根據共線方程得到誤差方程。

由于無人機拍攝具有5個自由度，因此共線條件方程線性化需要對五個角度分別展開并取一次小值項：

其中，(xc,yc)表示目標成像元素的像素坐標。dxs,dys,dzs,dγ,dω,dφ,dκ為目標坐標和五個角度的改正數。

則每個點的誤差方程式為：

其中，vx、vy分別表示在圖像坐標系的x軸、y軸方向上的成像誤差。在計算過程中，將地面控制點的大地坐標(x,y,z)視為真值，并把相應的像素坐標(x,y)視為觀測值。

若將上式各系數用a11,...,a28表示，則可寫成：

其中中間參數

用矩陣形式表示為：

v＝ax-l(6)

式中

(4)計算各改正數的系數。

為書寫方便，將共線方程中的分子、分母表示為如下：

則可以計算出系數：

由于

所以有

(5)逐個控制點計算，得到法方程，求解得改正數dxs,dys,dzs,dγ,dω,dφ,dκ。

第二步，計算相鄰幀圖像的重疊率。

獲取下一幀圖像作為當前幀圖像，每獲取一幀圖像均與上一幀圖像計算重疊率，若在重疊區域中有足夠多的同名點，則繼續執行下面步驟，進行連續幀間校正定位。

第三步，誤差粗估計。

通過對無人機各個姿態角誤差的分析，可以得出結論，無人機的姿態角誤差具有一定的連續性。而當無人機以高重疊率進行航拍的過程中，其各個姿態角必定都在進行緩慢平滑的變化。因此連續的兩幀圖像對應的姿態角的誤差也應該成連續變化。因此，本發明提出了姿態信息誤差的粗校正方法，如圖3所示。

即對當前幀圖像進行校正前，先利用上一幀圖像的各個姿態信息的誤差，即得到的改正數dxs,dys,dzs,dγ,dω,dφ,dκ對該幀圖像的姿態信息進行一次粗校正，進行粗校正后的姿態信息為近似值，再利用近似值進行后續的計算。同時，利用當前幀圖像的姿態信息的近似值將粗校正誤差進行更新，通過第一步中單幀圖像的定位反向校正的方法，獲取新的姿態信息改正數，以進行下面步驟。

通過加入姿態信息的粗校正，可以使得迭代次數明顯減少，而且也很大程度上避免了在迭代過程中陷入局部最優的情況，從而提高了誤差計算的準確度。

第四步，根據共面條件建立方程。

傳統的基于共面條件的相對-絕對定位方法，根據共面條件建立方程需要兩步。本發明改進了傳統方法，不僅細化了姿態角，而且本發明根據各個坐標之間的變換關系和矢量的運算性質，利用無人機提供的遙測數據與共面條件相結合，將幾何模型的確定與地理位置的計算整合到一步完成，使得f表達式里面的物理意義一步到位，計算出來的結果就是坐標真實值，而不用再進行絕對定位的計算。

由于以各個航拍位置為原點的東北天坐標系之間滿足平移關系，東北天坐標系與空間直角坐標系之間滿足平移和縮放變換，而共面條件下的矢量關系不會受到平移、縮放的影響，依然成立。因此本發明提出了將各矢量轉化為航拍圖像對應的東北天坐標系下，如圖4所示，在一步中同時完成目標模型的建立和目標點在東北天坐標系下的求解。

從兩個不同拍攝位置對同一目標進行航拍時，可以建立如圖4所示的幾何關系。其中m為同一目標點(同名點)，m1、m2為共同點m分別在兩幀圖像中的對應的像素點，則s1m1m與s2m2m表示兩幀圖像各自的攝像機光學中心s1、s2與共同點m之間的連線，又稱為同名光線。此時，顯然有兩個同名光線在同一平面中，即兩同名光線(s1m1m、s2m2m)與s1s2滿足共面條件。這也意味著只要滿足共面條件，就能使得同名光線對應相交。設s2處為無人機拍攝當前幀圖像時攝像機光學中心位置，s1處為無人機拍攝上一幀圖像時的攝像機光學中心位置。

在圖4中，設

其中，[xs2ys2zs2]和[xs1ys1zs1]分別是拍攝兩幀圖像時攝像機光學中心在東北天坐標系下的坐標，[bxbybz]為攝像機光學中心的位移矢量。

[xc1yc1zc1]^τ與[xc2yc2zc2]^τ為同名點m在兩幀圖像中對應的像素坐標，其中的坐標zc1＝zc2＝-f。[xn1yn1zn1]^τ與[xn2yn2zn2]^τ為兩像素坐標經過坐標系轉換后在各自對應的東北天坐標系下的坐標。因此，可以改用坐標的形式表示共面條件：

f表示外積，兩線共面，外積等于0。

由于引入了無人機航拍圖像對應的具有較高準確度的位置信息，因此在幀間的校正定位過程中，需要校正的元素只有后幀圖像對應的5個姿態角(平臺高低角平臺方位角γ，飛機俯仰角φ，飛機橫滾角ω，飛機航向角κ)。因為式(14)為非線性函數，根據多元函數泰勒展開保留小值一次項得：

其中f0為利用近似值根據式(14)計算求得的f值。

第五步，建立f的誤差方程。

根據觀測值+觀測值改正數＝近似值+近似值改正數的原則建立誤差方程式，如下：

其中，vf為f的誤差。

寫作矩陣形式為：

v＝ax-l(17)

其中：

下面對誤差方程式中的系數進行推導。

由式子(14)可知偏導數

其中，因為

所以

帶入(19)式即可得到對應的偏導數。利用同樣的方法可以計算出其余偏導數。

第六步，求解姿態信息的改正數。

遍歷所有同名點得到法方程，求解得到改正數。

對各個同名點重復上述第四步和第五步的操作，得到法方程如下：

a^τax＝a^τl(23)

公式(23)中，a，x如(18)中定義，l是公式(18)中多個l組成的矩陣。并根據

x＝(a^τa)^-1a^τl(24)

求解可以得到當前幀圖像各個姿態的改正數。

第七步，將改正數加到當前幀圖像的姿態信息的近似值上作為新的近似值，并判斷得到的改正數是否低于設定的限值，若是，停止迭代，輸出當前幀圖像的姿態信息的近似值以及各姿態的改正數，以用于下一幀圖像的計算中。否則，繼續利用當前幀圖像的姿態信息的新的近似值進行迭代，轉第四步執行。

當光軸斜視角增大時，例如從40度到70度，本發明提出的基于幀間連續性的多幀圖像目標定位校正方法與基本目標定位校正方法的誤差比較如圖5所示，可以看出本發明提出的方法具有更高的穩定性，定位誤差更小，并提高了定位準確度。