一種不同電氣元件構成系統中元件維修率分布確定方法與流程
本發明涉及電氣安全系統工程,特別是涉及環境因素變化時的不同元件構成電氣系統中元件維修率分布確定。
背景技術:
安全系統工程中相關的可靠性概念眾多,失效率、可靠度、維修度等等,其確定方法更是多種多樣,依實際問題而定,那么在不同影響條件下,系統結構不變時,系統和元件的上述參數并不是一成不變的,因為元器件受到本身物理材料的限制在不同環境下體現出來的物理性質略有不同,這些不同將直接導致元件功能性的改變,進而改變其可靠性,系統由基本元件組成,元件可靠性改變必將導致系統可靠性的改變,可靠性的改變將進一步導致失效率、可靠度、維修度等參數改變,那么如何表示這些參數受工作環境影響發生的改變就是一個必須面對的問題,目前關于可靠性受環境影響的研究已有較多,這些研究針對了各自領域的具體問題提出了解決方法,但難以形成完整的理論體系,也難以應用到其他領域的類似問題。
空間故障樹SFT(SpaceFaultTree,SFT)理論包括:連續型空間故障樹(Continuous Space Fault Tree,CSFT)和離散型空間故障樹(Discrete Space Fault Tree,DSFT),前者以了解系統結構和基本事件的性質為前提,從系統內部出發研究整個系統的可靠性,是由里及表的研究;后者以充分的實際故障觀測數據為前提,從系統外部的系統對于工作環境的故障響應來分析系統的可靠性,是由表及里的分析,CSFT經過已有的發展,已形成了等效于經典故障樹的對應概念,SFT中心思想之一就是使用特征函數表示影響因素與故障概率之間的關系,即構成以影響因素為自變量,故障概率為因變量的函數,所以SFT理論可表示影響因素與故障概率之間的關系。
這里研究的是維修度與因素影響之間的關系,我們知道,系統的可靠性變化可用Markov狀態轉移圖和矩陣表示,Markov狀態轉移矩陣中一般包含失效率、維修率和狀態轉移概率等,其失效率可用SFT中故障概率分布表示,只要按照一定條件合理的設定狀態轉移概率,通過狀態轉移概率算式求解便得到元件維修率,SFT下的維修率改為維修率分布,基于上述思想對不同元件組成并聯和串聯系統中元件維修率分布進行推導,通過實例分析得到了元件維修率分布和狀態轉移概率。
技術實現要素:
1.一種不同電氣元件構成系統中元件維修率分布確定方法,其特征在于,計算可表示環境因素影響的電氣元件維修率分布,因素包括:使用時間t和使用溫度c;給出針對不同元件構成的串聯、并聯和混聯電氣系統中元件的維修率分布計算方法;給出串聯和并聯系統中元件維修率推導過程;對狀態轉移概率根據Markov狀態轉移圖中的狀態關系求解;使用SFT中的元件故障概率分布代替Markov鏈中的失效率,可得到電氣元件維修率分布;可用于環境因素變化時的不同元件構成電氣系統中元件維修率分布確定。
2.根據權利要求1所述一種不同電氣元件構成系統中元件維修率分布確定方法,其特征在于設電氣系統有n個不同元件組成,通過串聯形式構成電氣系統;λi和μi分別表示第i個電氣元件的失效率和維修率;當t→∞時,狀態轉移概率如式(2):
求解式(2)得
3.根據權利要求1所述一種不同電氣元件構成系統中元件維修率分布確定方法,其特征在于對狀態轉移概率根據Markov狀態轉移圖中的狀態關系求解;對于串聯系統p0與p1是一種概率轉化關系,可得進而又因為則得到這種方法即為根據Markov狀態轉移圖的狀態關系求解方法。
4.根據權利要求1所述一種不同電氣元件構成系統中元件維修率分布確定方法,其特征在于設電氣系統有n個不電氣同元件組成,通過并聯形式構成電氣系統,當t→∞時狀態轉移概率如式(4)所示:
式(4)與聯立,可解得
5.根據權利要求1所述一種不同電氣元件構成系統中元件維修率分布確定方法,其特征在于對狀態轉移概率根據Markov狀態轉移圖中的狀態關系求解;對于并聯電氣系統使用狀態關系求解,與p0直接轉化的狀態pi具有關系那么pi繼續向外延伸狀態鏈與pi+1轉化具有關系依次類推,加之便可得到p0結果。
6.根據權利要求1所述一種不同電氣元件構成系統中元件維修率分布確定方法,其特征在于點系統是由不同類型元件組成的,所以元件失效率λi、維修率μi和狀態轉移概率pi各不相同,λi可由SFT理論中的元件故障概率分布提供;當計算得到的維修率μi大于1時取1。
7.根據權利要求1所述一種不同電氣元件構成系統中元件維修率分布確定方法,其特征在于不同元件的維修率分布為式(5):
將SFT中提供的元件故障概率分布代替式(5)中的λi,則可轉化為SFT下的電氣元件維修率分布;元件故障概率分布用Pi(x1,x2,…xd)表示,即其中d為影響因素個數;Pik(xk)表示系統中第i個元件的第k個因素影響下的故障概率特征函數;即在單一因素影響下,隨影響因素的變化表現出來的發生概率變化特征的表示函數;用Pik(xk)表示,i表示第i個元件,k表示影響因素,xk表示該因素的具體數值;元件維修率在SFT下的表示定義為元件維修率分布;元件維修率分布是一個以系統工作環境因素為參數的函數。
8.根據權利要求1所述一種不同電氣元件構成系統中元件維修率分布確定方法,其特征在于電氣系統,由三個相同元件組成,為混聯系統,該系統的故障概率影響因素為使用時間t和使用溫度c,
對于該例求解p0和p1~7用狀態關系求解,與聯立,解得一般情況下維修率大于故障率取極限情況為1,則最終0.1≤p0≤0.625,引入SFT中的元件故障概率分布,元件X1、X2、X3代替,三個元件的特征函數如式(9)所示,將是(9)帶入式(8)得式(10),從而計算這些元件的維修率分布,,維修率大于1時取1,
λi=Pi(t,c)=1-(1-Pit(t))(1-Pic(c)),i=1,2,3 (9),
1利用Markov狀態轉移鏈確定不同元件維修度。
1.1串聯系統不同元件維修度。
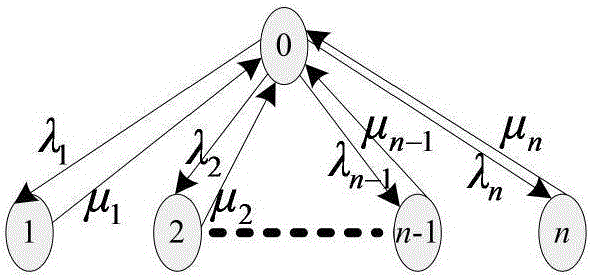
參考Markov狀態轉移鏈的表述方法,設系統有n個不同元件組成,通過串聯形式構成系統,其框圖如圖1所示,狀態的定義如式(1)所示,對應的Markov狀態轉移鏈如圖2所示,
圖2中的λi和μi分別表示第i個元件的失效率和維修率,只有在0狀態時系統功能是正常的,當t→∞時,狀態轉移概率是趨于與初始值無關的常數,得到式(2),
求解式(2)得直接解式(2)較為困難,那么從圖2來看p0與p1是一種概率轉化關系,可得進而又因為則得到與上述方程結果相同,但簡便得多,這種方法即為根據Markov狀態轉移圖的狀態關系求解。
1.2并聯系統不同元件維修度。
設系統有n個不同元件組成,通過并聯形式構成系統,其框圖如圖3所示,狀態的定義如式(3)所示,對應的Markov狀態轉移鏈如圖4所示,
當t→∞時,得到穩定時的狀態轉移概率,如式(4)所示,
式(4)與聯立,可解得
使用狀態關系求解,與p0直接轉化的狀態pi具有關系那么pi繼續向外延伸狀態鏈與pi+1轉化具有關系依次類推,加之便可得到上述p0結果。
系統是由不同類型元件組成的,所以元件失效率λi、維修率μi和狀態轉移概率pi各不相同,λi可由SFT理論中的元件故障概率分布提供,p0可根據實際要求進行合理設置,p0取值范圍依賴于實際系統結構,當計算得到的維修率μi大于1時取1。
2SFT中不同元件的維修率分布。
上節的理論推導可總結為式(5),
將SFT中提供的元件故障概率分布代替式(5)中的λi,則可轉化為SFT下的元件維修率分布,元件故障概率分布用Pi(x1,x2,…xd)表示,即其中d為影響因素個數,Pik(xk)表示系統中第i個元件的第k個因素影響下的故障概率特征函數,即在單一因素影響下,隨影響因素的變化表現出來的發生概率變化特征的表示函數,可以是初等函數,分段函數等,用Pik(xk)表示,i表示第i個元件,k表示影響因素,xk表示該因素的具體數值。
元件維修率在SFT下的表示定義為元件維修率分布,元件維修率分布是一個以系統工作環境因素為參數的函數。
附圖說明
圖1串聯系統框圖。
圖2串聯系統狀態轉移。
圖3并聯系統框圖。
圖4并聯系統狀態轉移。
圖5混聯系統框圖。
圖6混聯系統狀態轉移。
圖7元件的維修率分布p0=0.5(a)元件X1的維修率分布 (b)元件X2的維修率分布 (c)元件X3的維修率分布。
具體實施方式
實例分析對象為一簡單電氣系統,由三個相同元件組成,為混聯系統,如圖5所示,相應的狀態定義如式(6)所示,狀態轉移如圖6所示,該系統的故障概率影響因素為使用時間t和使用溫度c,
對于該例求解p0和p1~7不使用轉移狀態矩陣求解,而用狀態關系求解,與聯立,解得一般情況下維修率大于故障率,元件才能正常工作,那么取極限情況為1,則最終0.1≤p0≤0.625,該解只與系統結構有關。
引入SFT中的元件故障概率分布,設圖5中的三個元件各不相同,分別用元件X1、X2、X3代替,三個元件的特征函數如式(9)所示,式中Pit(t)和Pic(c)如表1所示,將是(9)帶入式(8)得式(10),從而計算這些元件的維修率分布,當p0=0.5時,如圖7所示,維修率大于1時取1,
λi=Pi(t,c)=1-(1-Pit(t))(1-Pic(c)),i=1,2,3 (9),
表1 Pit(t)和Pic(c)的表達式
從圖7可知,得到的元件維修率分布是考慮使用時間t和使用溫度c的元件維修率,且滿足推導過程中維修率大于故障率的假設,元件維修率分布對于不同工作環境下的元件維修率的確定提供了有效依據和方法,較傳統維修率確定方法更為精確。
實際上,通過分析發現當系統元件連接結構固定后,的值有一定關系,取決于i狀態距0狀態距離有多遠(狀態轉移次數),狀態轉移次數相同的一類狀態的是相同的;而轉移次數越多越小。
- 還沒有人留言評論。精彩留言會獲得點贊!