本發明涉及自動控制技術領域，特別是指一種針對仿生撲翼飛行機器人的控制方法。

背景技術：

近年來，隨著人們對無人機技術需求的持續增加，以及先進制造技術、新材料技術和新能源技術的飛速發展，使仿生撲翼飛行機器人的研究成為技術熱點。科學家們受到飛行昆蟲和蜂鳥的啟發，提出了仿生撲翼飛行機器人的概念，并制造出多種仿生撲翼飛行機器人。仿生撲翼飛行機器人的優點是體積小，擅長低空飛行，并具有優秀的懸停能力和盤旋能力。這些突出的優點對目標在特定環境下的搜尋，救援以及軍事偵察提供了可能。

六自由度仿生撲翼飛行機器人系統的動態模型是很復雜的。雖然對動態模型進行了簡化，但還是有很多模型參數需要獲取。然而，有些模型參數不能被測量。即使可以測得，也需要大量的傳感器，付出很高的代價，并影響控制精度。因此，需要使用可減小仿生撲翼飛行機器人對動態模型參數需求的控制方法來設計控制器。由于神經網絡能很好地近似許多種類的非線性參數，可以使用神經網絡控制方法控制仿生撲翼飛行機器人。

目前，有關仿生撲翼飛行機器人的專利寥寥無幾，基于仿生撲翼飛行機器人模型設計的控制算法更是少之又少。

技術實現要素：

本發明要解決的技術問題是提供一種針對仿生撲翼飛行機器人的控制方法，能夠填補仿生撲翼飛行機器人控制算法的空白。

為解決上述技術問題，本發明實施例提供一種針對仿生撲翼飛行機器人的控制方法，包括：

對所述仿生撲翼飛行機器人進行運動學和動力學分析，建立拉格朗日型模型；

基于所述拉格朗日型模型，設計帶有擾動觀測器的基于模型的姿態控制器；

基于設計的帶有擾動觀測器的基于模型的姿態控制器，設計帶有擾動觀測器的神經網絡全狀態反饋姿態控制器；

基于所述仿生撲翼飛行機器人的位置控制模型，設計帶有擾動觀測器的基于模型的位置控制器；

根據設計的帶有擾動觀測器的基于模型的姿態控制器、神經網絡全狀態反饋姿態控制器及基于模型的位置控制器，對所述仿生撲翼飛行機器人的姿態和位置進行軌跡跟蹤控制。

進一步地，所述拉格朗日型模型表示為：

其中，D_r(q_r)、表示矩陣，D_r(q_r)＝I_pT，I_p表示轉動慣量矩陣，T表示由身體坐標系到慣性坐標系的坐標轉換矩陣，表示T對時間t的一階導數，L(t)表示一個使等式成立的矩陣，q_r是q_r(t)的簡寫形式，q_r(t)表示系統姿態狀態矩陣，是的簡寫形式，表示q_r(t)對時間t的一階導數，表示q_r(t)對時間t的二階導數，τ_r是τ_r(t)的簡寫形式，τ_r(t)表示仿生撲翼飛行機器人姿態控制輸入。

進一步地，所述帶有擾動觀測器的基于模型的姿態控制器表示為：

e_r1＝x_r1-x_r1d

e_r2＝x_r2-α_r1

e_r3＝d_r(t)-Φ(e_r2)

其中，τ_r1表示姿態控制器，x_r1＝q_r，x_r1表示姿態狀態矩陣q_r(t)，x_r2表示表示q_r(t)對時間t的一階導數，x_r1d是x_r1d(t)的簡寫形式，x_r1d(t)＝[θ_1d(t),θ_2d(t),θ_3d(t)]^T，θ_1d(t),θ_2d(t),θ_3d(t)分別是身體坐標系中的三個歐拉角要跟蹤的期望角度，K_r2表示控制增益，e_r1、e_r2表示狀態偏差，表示系統擾動d_r(t)的估計值，表示虛擬速度跟蹤軌跡α_r1對時間t的一階導數，e_r3為輔助函數，為e_r3的估計值，Φ(e_r2)關于e_r2的函數，為關于時間t的一階導數，K(e_r2)為Φ(e_r2)關于e_r2的導數，表示D_r(x_r1)的逆矩陣。

進一步地，所述帶有擾動觀測器的神經網絡全狀態反饋姿態控制器表示為：

e_r1＝x_r1-x_r1d

e_r2＝x_r2-α_r1

e_r3＝d_r(t)-Φ(e_r2)

其中，τ_r2表示神經網絡全狀態反饋姿態控制器，x_r1＝q_r，x_r1表示姿態狀態矩陣，x_r2表示表示姿態狀態矩陣對時間t的一階導數，x_r1d是x_r1d(t)的簡寫形式，x_r1d(t)＝[θ_1d(t),θ_2d(t),θ_3d(t)]^T，θ_1d(t),θ_2d(t),θ_3d(t)分別是身體坐標系中的三個歐拉角要跟蹤的期望角度，K_r2表示控制增益，e_r1、e_r2表示狀態偏差，表示系統擾動d_r(t)的估計值，C₀(x_r1,x_r2)表示C_r(x_r1,x_r2)的虛擬部分，α_r1表示虛擬速度跟蹤軌跡，表示神經網絡的權重估計值，表示的轉置，S(Z)表示神經網絡基函數，Z表示神經網絡的輸入，e_r3為輔助函數，為e_r3的估計值，Φ(e_r2)關于e_r2的函數，為關于時間t的一階導數，K(e_r2)為Φ(e_r2)關于e_r2的導數，表示D_r(x_r1)的逆矩陣，為表示D_r(x_r1)虛擬部分的逆矩陣。

進一步地，所述位置控制模型表示為：

其中，D_t、G_t表示矩陣，R^IB(q_r(t))表示坐標系變換陣，q_r(t)表示系統姿態狀態矩陣，是的簡寫形式，表示q_r(t)對時間t的二階導數，τ_t(t)表示位置控制器，d_t(t)表示系統擾動。

進一步地，所述帶有擾動觀測器的基于模型的位置控制器表示為：

e_t1＝x_t1-x_t1d

e_t2＝x_t2-α_t1

其中，τ_t為τ_t(t)的簡寫形式，τ_t表示位置控制器，q_r是q_r(t)的簡寫形式，(R^IB(q_r))^-1表示R^IB(q_r(t))的逆矩陣，x_t1＝q_t，x_t1、q_t表示位置變換狀態矩陣，x_t2、表示位置變換狀態矩陣q_t對時間t的一階導數，x_t1d(t)＝[x_d(t),y_d(t),z_d(t)]^T，x_d(t),y_d(t),z_d(t)分別表示大地坐標系x、y、z方向上要跟蹤的期望位置軌跡，e_t1、e_t2表示位置偏差，K_d、K_t4表示控制增益，表示系統擾動d_t(t)的估計值，表示虛擬速度跟蹤軌跡α_t1對時間t的一階導數。

進一步地，所述方法還包括：

采用李雅普諾夫直接法，分析加入所述帶有擾動觀測器的基于模型的姿態控制器后閉環系統的穩定性以及系統狀態的有界性，構造的李雅普諾夫函數表示為：

其中，V₁表示構造的李雅普諾夫函數，表示與d_r(t)之間的誤差，分別表示e_r1、e_r2、的轉置。

進一步地，所述方法還包括：

若e_r1、e_r2、都有界，則加入所述帶有擾動觀測器的基于模型的姿態控制器后閉環系統的系統狀態滿足有界性。

進一步地，所述方法還包括：

采用李雅普諾夫直接法，分析加入所述帶有擾動觀測器的神經網絡全狀態反饋姿態控制器后閉環系統的穩定性以及系統狀態的有界性，構造的李雅普諾夫函數表示為：

其中，V₂表示構造的李雅普諾夫函數，D₀(x_r1)表示D_r(x_r1)的虛擬部分，表示與d_r(t)之間的誤差，表示神經網絡的權重誤差，表示的轉置，表示預設的常數矩陣的逆矩陣，i＝1,2,3，n表示矩陣中元素的數目，分別表示e_r1、e_r2、的轉置。

進一步地，所述方法還包括：

采用李雅普諾夫直接法，分析加入所述帶有擾動觀測器的基于模型的位置控制器后閉環系統的穩定性以及系統狀態的有界性，構造的李雅普諾夫函數表示為：

其中，V₃表示構造的李雅普諾夫函數，表示與d_t(t)之間的誤差，分別表示e_t1、e_t2、的轉置。

本發明的上述技術方案的有益效果如下：

上述方案中，通過對所述仿生撲翼飛行機器人進行運動學和動力學分析，得到處理具有大量未知系統參數的拉格朗日型模型；基于所述拉格朗日型模型，設計帶有擾動觀測器的基于模型的姿態控制器；基于設計的帶有擾動觀測器的基于模型的姿態控制器，設計帶有擾動觀測器的神經網絡全狀態反饋姿態控制器；基于所述仿生撲翼飛行機器人的位置控制模型，設計帶有擾動觀測器的基于模型的位置控制器；根據設計的帶有擾動觀測器的基于模型的姿態控制器、神經網絡全狀態反饋姿態控制器及基于模型的位置控制器，只需要較少的傳感器和執行器，就能有效地對仿生撲翼飛行機器人的姿態和位置進行軌跡跟蹤控制。

附圖說明

圖1為本發明實施例提供的針對仿生撲翼飛行機器人的控制方法的流程示意圖；

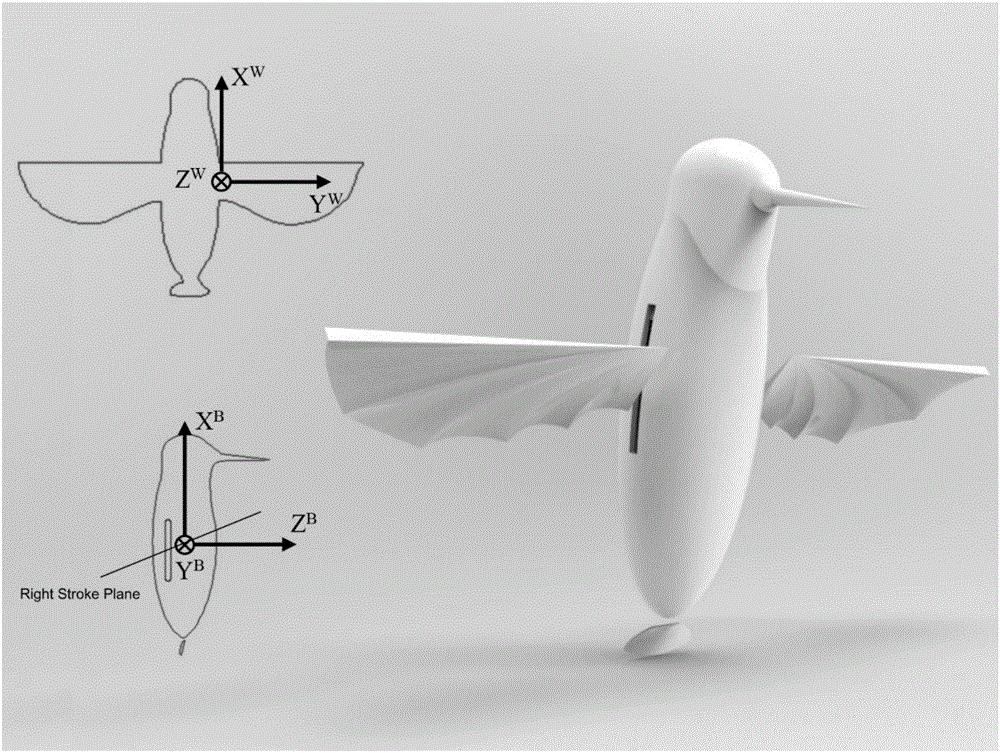
圖2為本發明實施例提供的仿生撲翼飛行機器人的結構示意圖；

圖3為本發明實施例提供的系統在帶有擾動觀測器的基于模型的姿態控制器控制下的仿真效果圖；

圖4為本發明實施例提供的帶有擾動觀測器的姿態控制輸入；

圖5為本發明實施例提供的系統在帶有擾動觀測器的基于模型的位置控制器控制下的仿真效果圖；

圖6為本發明實施例提供的帶有擾動觀測器的基于模型的位置控制輸入示意圖；

圖7為本發明實施例提供的系統在帶有擾動觀測器的神經網絡全狀態反饋姿態控制器控制下的仿真效果圖；

圖8為本發明實施例提供的帶有擾動觀測器的神經網絡全狀態反饋姿態控制輸入；

圖9為本發明實施例提供的系統在帶有擾動觀測器的基于模型的位置控制器控制下的仿真效果圖；

圖10為本發明實施例提供的帶有擾動觀測器的基于模型的位置控制輸入示意圖。

具體實施方式

為使本發明要解決的技術問題、技術方案和優點更加清楚，下面將結合附圖及具體實施例進行詳細描述。

為了更好地理解本實施例，先對本文中的一些簡寫進行舉例說明，例如，q_r是q_r(t)的簡寫形式，是的簡寫形式，是的簡寫形式，τ_r是τ_r(t)的簡寫形式，τ_t為τ_t(t)的簡寫形式，x_r1d是x_r1d(t)的簡寫形式，其他類似的簡寫不再一一說明。

本文中，形式為表示一階導數，表示二階導數，在沒有特殊說明的情況下，都是對時間t進行求導，例如，為w對時間t的一階導數。

參看圖1所示，本發明實施例提供的針對仿生撲翼飛行機器人的控制方法，包括：

S101，對所述仿生撲翼飛行機器人進行運動學和動力學分析，建立拉格朗日型模型；

S102，基于所述拉格朗日型模型，設計帶有擾動觀測器的基于模型的姿態控制器；

S103，基于設計的帶有擾動觀測器的基于模型的姿態控制器，設計帶有擾動觀測器的神經網絡全狀態反饋姿態控制器；

S104，基于所述仿生撲翼飛行機器人的位置控制模型，設計帶有擾動觀測器的基于模型的位置控制器；

S105，根據設計的帶有擾動觀測器的基于模型的姿態控制器、神經網絡全狀態反饋姿態控制器及基于模型的位置控制器，對所述仿生撲翼飛行機器人的姿態和位置進行軌跡跟蹤控制。

本發明實施例所述的針對仿生撲翼飛行機器人的控制方法，通過對所述仿生撲翼飛行機器人進行運動學和動力學分析，得到處理具有大量未知系統參數的拉格朗日型模型；基于所述拉格朗日型模型，設計帶有擾動觀測器的基于模型的姿態控制器；基于設計的帶有擾動觀測器的基于模型的姿態控制器，設計帶有擾動觀測器的神經網絡全狀態反饋姿態控制器；基于所述仿生撲翼飛行機器人的位置控制模型，設計帶有擾動觀測器的基于模型的位置控制器；根據設計的帶有擾動觀測器的基于模型的姿態控制器、神經網絡全狀態反饋姿態控制器及基于模型的位置控制器，只需要較少的傳感器和執行器，就能有效地對仿生撲翼飛行機器人的姿態和位置進行軌跡跟蹤控制。

本實施例提供的針對仿生撲翼飛行機器人的控制方法具體步驟可以包括：

步驟1，如圖2所示為仿生撲翼飛行機器人的結構示意圖，所述仿生撲翼飛行機器人可以是六自由度仿生撲翼飛行機器人，通過對所述六自由度仿生撲翼飛行機器人進行運動學和動力學分析，得到：

其中，I_p為轉動慣量矩陣，w為由身體坐標系的三個歐拉角經坐標轉換到慣性坐標系的角速，q_r(t)表示系統姿態狀態矩陣，T是由身體坐標系到慣性坐標系的坐標轉換矩陣。

令其中，L(t)是一個使等式成立的矩陣，無實際意義，得到拉格朗日型模型：

式(2)中，矩陣D_r(q_r)＝I_pT，和D_r(q_r)無實際意義，用于簡化拉格朗日型模型的表達形式；系統姿態狀態矩陣q_r(t)＝[θ₁ θ₂ θ₃]^T，θ₁、θ₂、θ₃是身體坐標系中的三個歐拉角，分別是俯仰角、扭轉角、偏航角；表示系統姿態狀態矩陣q_r(t)對時間t的二階導數，τ_r表示撲翼飛行器姿態控制輸入，由身體坐標系到慣性坐標系的坐標轉換矩陣T表示為：

令x_r1＝q_r＝[θ₁,θ₂,θ₃]^T以及于是得到：

其中，d_r(t)為系統擾動，是D_r(x_r1)的逆矩陣，是x_r1對時間t的一階導數，是x_r2對t的一階導數。

設計帶有擾動觀測器的基于模型的姿態控制器時，x_r1和x_r2是已知狀態變量，設x_r1d(t)＝[θ_1d(t),θ_2d(t),θ_3d(t)]^T，其中，θ_1d(t),θ_2d(t),θ_3d(t)分別是身體坐標系中的三個歐拉角(俯仰角，扭轉角，偏航角)要跟蹤的期望角度，則跟蹤的狀態偏差分別為：

式(4)中，e_r1、e_r2表示狀態偏差，虛擬速度跟蹤軌跡其中，A_r1＝K_r1e_r1，K_r1≥0為控制增益。

根據式(3)，對式(4)兩邊求關于時間t的導數得：

基于式(6)拉格朗日型模型，設計擾動觀測器，對控制器進行優化處理，設輔助函數為：

e_r3＝d_r(t)-Φ(e_r2) (7)

其中，Φ(e_r2)為關于e_r2的函數

對式(8)兩邊求關于時間t的導數得

其中，Φ(e_r2)關于e_r2的導數為

令的估計值為

又有擾動變量的估計值為

得到e_r3的誤差

所以可得干擾的誤差關于時間t的導數

為了證明加入姿態控制器后系統的穩定性和一直有界性，構造李雅普諾夫函數如下

對式(12)兩邊求關于時間t的導數得

K_r1≥0為控制增益，設D_r(x_r1)和C_r(x_r1,x_r2)是已知的，設計帶有擾動觀測器的基于拉格朗日型模型的姿態控制器為：

其中，τ_r1為基于拉格朗日型模型的姿態控制器，K_r2≥0為控制增益；

令其中，γ為大于零的常數，得系統是穩定的以及狀態是有界的

其中，式(16)中ε₁，C₁為大于0的常數

其中，γ為大于零的常數，為了保證ε₁>0，系統參數需滿足

λ_min(K_r1)>0

其中，I表示單位矩陣，λ_min(·)和λ_max(·)為矩陣·的最小特征值和最大特征值。

對式(18)兩邊同時乘以得

對式(20)兩邊積分得

因此，狀態偏差e_r1有界，同理可得e_r2，有界，因此，加入所述帶有擾動觀測器的基于模型的姿態控制器后閉環系統的系統狀態滿足有界性。

步驟2，基于設計的帶有擾動觀測器的基于模型的姿態控制器，設計帶有擾動觀測器的神經網絡全狀態反饋姿態控制器，采用李雅普諾夫直接法來分析加入神經網絡全狀態反饋姿態控制器后閉環系統的穩定性以及系統狀態的有界性。

針對撲翼飛行機器人設計神經網絡全狀態反饋控制器，把D_r(x_r1)和C_r(x_r1,x_r2)分成倆部分，虛擬部分設一個已知的D₀(x_r1)，則不確定的部分為ΔD_r(x_r1)＝D_r(x_r1)-D₀(x_r1)。同理，設虛擬部分為C₀(x_r1,x_r2)，C₀(x_r1,x_r2)是反對稱矩陣以及不確定部分為ΔC_r(x_r1,x_r2)＝C_r(x_r1,x_r2)-C₀(x_r1,x_r2)。

設計帶有擾動觀測器的神經網絡全狀態反饋控制器為：

其中，τ_r2為神經網絡全狀態反饋控制器，用于估計神經網絡W^*TS(Z)，其中，和W^*為神經網絡的權重誤差，估計值和真實值，S(Z)為神經網絡基函數。

其中，是神經網絡的輸入，∈(Z)是神經網絡的近似偏差。

神經網絡的自適應律為

其中，常數Γ_i,i＝1,2,3為控制增益矩陣，小的正數σ_i>0,i＝1,2,3。

根據式(21)，重新定義式(5)為

擾動觀測器輔助函數與基于拉格朗日型模型控制時一樣，同理可得

設輔助函數的估計值為

同理可得

因此

設計李雅普諾夫方程為

n表示矩陣中元素的數目，對式(28)兩邊求關于時間t的導得

代入式(20)，(21)，(282)，(297)于(30)中得

化簡得

由于S(Z)<s，其中S(Z)為RBF神經網絡基函數，s為正數。最終得

其中，C₂為常數；

為了保證常數ε₂>0，系統參數需滿足

λ_min(K_r1)>0,λ_min(K_r2-I)>0,

λ_min[K(e_r2)D₀(x_r1)^-1-(||K(e_r2)D₀(x_r1)^-1||²+1)I]>0

和設計的帶有擾動觀測器的基于模型的姿態控制器一樣，有e_r1，e_r2，有界，即：加入所述帶有擾動觀測器的神經網絡全狀態反饋姿態控制器后閉環系統的系統狀態滿足有界性。

步驟3，基于所述仿生撲翼飛行機器人的位置控制模型，設計帶有擾動觀測器的基于模型的位置控制器，采用李雅普諾夫直接法來分析加入位置控制器后閉環系統的穩定性以及系統狀態的有界性：

六自由度仿生撲翼飛行機器人的位置控制模型為

其中，以及坐標系變換陣而且R^IB(q_r(t))＝(R^BI(q_r(t)))^-1；其中，D_t、G_t均無實際意義，只是用來簡化公式，m是仿生撲翼飛行機器人總質量，g表示重力系數，mg是仿生撲翼飛行機器人的重力，τ_t為τ_t(t)的簡寫形式，τ_t(t)表示位置控制器，d_t(t)為系統擾動。

令x_t1＝q_t＝[x,y,z]^T和得

其中，q_t＝[x,y,z]^T為位置變換狀態矩陣

在設計基于模型的控制器時，認為x_t1和x_t2已知，x_t1d(t)＝[x_d(t),y_d(t),z_d(t)]^T，其中，x_d(t),y_d(t),z_d(t)分別是大地坐標系x、y、z方向上要跟蹤的期望位置軌跡，則跟蹤位置偏差為

式(37)中，e_t1、e_t2表示位置狀態偏差，虛擬速度跟蹤軌跡A_t1＝K_t3e_t1，K_t3≥0為控制增益。

把式(36)代入式(37)中得

為設計擾動觀測器，設輔助函數為

e_t3＝d_t(t)-K_de_t2 (35)

其中，K_d>0為擾動觀測器控制增益。

對輔助函數兩邊求關于時間t的導數得

令輔助函數的估計值為

因此

得

設李雅普諾夫函數為

對李雅普諾夫函數兩邊求關于時間t的導數得

設計帶有擾動觀測器基于所述仿生撲翼飛行機器人的位置控制模型的位置控制器為

其中，K_t4≥0為控制增益。

最后得到

其中，

其中，C₃為常數；

為了保證常數ε₃>0，系統參數需滿足

和設計的帶有擾動觀測器的基于模型的姿態控制器一樣，有e_t1，e_t2，有界，即：加入所述帶有擾動觀測器的基于模型的位置控制器后閉環系統的系統狀態滿足有界性。

步驟4：根據設計的帶有擾動觀測器的基于模型的姿態控制器、神經網絡全狀態反饋姿態控制器及基于模型的位置控制器，對所述仿生撲翼飛行機器人的姿態和位置進行軌跡跟蹤控制：

本實施例中，將基于MATLAB平臺進行數值仿真，驗證針對仿生撲翼飛行機器人姿態和位置控制設計的帶有擾動觀測器的基于模型的姿態控制器、神經網絡全狀態反饋姿態控制器及基于模型的位置控制器的控制效果，系統參數選取如下表1：

表1仿生撲翼飛行機器人參數表

對仿生撲翼飛行機器人的姿態和位置進行軌跡跟蹤控制，姿態追蹤軌跡選為位置追蹤軌跡為又假設姿態控制以及位置控制的干擾均為狀態變量初值：x_r1(0)＝[0.01,0.01,0.01]^T，x_r2(0)＝[0.01,0.01,0.01]^T，x_t1(0)＝[0.01,0.01,0.01]^T，x_t2(0)＝[0.01,0.01,0.01]^T。

在設計基于模型的控制器時，控制增益選為：K_r1＝500，K_r2＝500，K(e_r2)＝30，K_t3＝600，K_t4＝600，K_d＝5。

則由圖3和圖5可知，本文設計的帶有擾動觀測器的基于模型的姿態控制器和位置控制器能夠有效的對仿生撲翼飛行機器人的姿態和位置進行軌跡跟蹤控制，由圖4和圖6可知，姿態控制器和位置控制器可以實現。

再根據設計的帶有擾動觀測器的基于模型的姿態控制器，設計帶有擾動觀測器的神經網絡全狀態反饋姿態控制器時，控制增益設定為：K_r1＝300，K_r2＝300，K(e_r2)＝50，K_t3＝500，K_t4＝500，K_d＝10，σ₁＝0.02，σ₂＝0.02，σ₃＝0.02，Γ₁＝100I，Γ₂＝100I，Γ₃＝100I。

則由圖7和圖9可知，本文設計的帶有擾動觀測器的神經網絡全狀態反饋姿態控制器和帶有擾動觀測器的基于模型的位置控制器能夠有效的對仿生撲翼飛行機器人的姿態和位置進行軌跡跟蹤控制。由圖8和圖10可知，神經網絡全狀態反饋姿態控制器及基于模型的位置控制器可以實現。

以上所述是本發明的優選實施方式，應當指出，對于本技術領域的普通技術人員來說，在不脫離本發明所述原理的前提下，還可以做出若干改進和潤飾，這些改進和潤飾也應視為本發明的保護范圍。