一種含干擾觀測器的高超聲速飛行器跟蹤控制方法與流程
本發明涉及含干擾觀測器的高超聲速飛行器跟蹤控制方法。
背景技術:
高超聲速飛行器是指飛行速度大于5馬赫的飛行器,其速度快、突防能力強,有著巨大的軍事價值和經濟價值(Dydek Z T,Annaswamy A M,Lavretsky E.Adaptive control and the NASA X-15-3flight revisited[J].Control Systems,IEEE,2010,30(3):32-48)。然而,由于其采用了發動機/機體的一體化設計,導致機體結構和推進系統之間的強耦合以及動力學系統具有復雜非線性特性(Bolender M A,Doman D B.Nonlinear longitudinal dynamical model of an air-breathing hypersonic vehicle[J].Journal of Spacecraft and Rockets,2007,44(2):374-387)。另外由于飛行器巡航過程中的燃料消耗、氣動熱引起的機體形變等因素會使模型產生較大的不確定性(Sigthorsson D,Jankovsky P,Serrani A,et al.Robust linear output feedback control of an airbreathing hypersonic vehicle[J].Journal of Guidance,Control,and Dynamics,2008,31(4):1052-1066)。由上述可知,高超聲速飛行器飛行包線大、飛行環境復雜,具有氣動特性變化劇烈,模型不確定性強等特點。這些特點使得對其控制系統設計面臨著巨大的挑戰。
近年來各類非線性控制算法日漸成熟,并逐漸應用于高超聲速飛行器的控制器設計中。文獻(Watts A C.Control of a High Performance Maneuvering Reentry Vehicle Using Dynamic Inversion{C}[C]//AIAA Guidance,Navigation,and Control Conference and Exhibit.2005:1-16),(Mathavaraj S,Halbe O,Padhi R.Robust control of a reusable launch vehicle in reentry phase using model following neuro-adaptive design[C]//Proceedings of the AIAA Guidance,Navigation,and Control Conference.2010:2-5),(Parker J T,Serrani A,Yurkovich S,et al.Control-oriented modeling of an air-breathing hypersonic vehicle[J].Journal of Guidance,Control,and Dynamics,2007,30(3):856-869)利用系統的輸出線性化方法對高超聲速飛行器進行控制器設計。然而,基于動態逆或反饋線性化的方法要求高超聲速飛行器模型具備反饋線性化的條件,而這在實際情況中通常無法滿足,另外,當被控對象中有不確定性參數或者未建模動態存在時,不能保證其魯棒性,需要與其他的魯棒控制方法結合使用(Burken J J,Lu P,Wu Z L.Reconfigurable flight control designs with application to the X-33vehicle[C].AIAA Guidanee,Navigation,and Control Conference and Exhibit,AIAA1999-4134),(Bu X,Wu X,Ma Z,et al.Novel adaptive neural control of flexible air-breathing hypersonic vehicles based on sliding mode differentiator[J].Chinese Journal of Aeronautics,2015,28(4):1209-1216)。為了滿足實際工程中對系統在有限時間內穩定的需求,有限時間控制方法相比于漸近穩定和指數穩定控制方法具有實際意義和理論價值。自文獻(Zhu Z,Xia Y,Fu M.Attitude stabilization of rigid spacecraft with finite‐time convergence[J].International Journal of Robust and Nonlinear Control,2011,21(6):686-702),(Yu X,Man Z.Model reference adaptive control systems with terminal sliding modes[J].International Journal of Control,1996,64(6):1165-1176)提出了有限時間終端滑模控制理論以來,基于滑模的有限時間控制理論受到廣泛關注。對于傳統終端滑模控制中存在的控制奇異和遠離平衡點時收斂緩慢的兩個問題。為了解決終端滑模控制的奇異問題,文獻(Feng Y,Yu X,Han F.On nonsingular terminal sliding-mode control of nonlinear systems[J].Automatica,2013,49(6):1715-1722)通過引入新型飽和函數避免了終端滑模控制器奇異問題。文獻(Mu C,Sun C,Xu W.Fast sliding mode control on air-breathing hypersonic vehicles with transient response analysis[J].Proceedings of the Institution of Mechanical Engineers,Part I:Journal of Systems and Control Engineering,2016,230(1):23-34),(Feng Y,Yu X,Man Z.Non-singular terminal sliding mode control of rigid manipulators[J].Automatica,2002,38(12):2159-2167),(Yang L,Yang J.Nonsingular fast terminal sliding‐mode control for nonlinear dynamical systems[J].International Journal of Robust and Nonlinear Control,2011,21(16):1865-1879),(Xu S S D,Chen C C,Wu Z L.Study of nonsingular fast terminal sliding-mode fault-tolerant control[J].IEEE Transactions on Industrial Electronics,2015,62(6):3906-3913),(Xiaohu Z X W,Gongzhang Z J S.Disturbance compensated terminal sliding mode control for hypersonic vehicles[J].Journal of Beijing University of Aeronautics and Astronautics,2012,11:008)基于非奇異終端滑模理論,設計了非奇異終端滑模有限時間控制器。文獻(Mu C,Sun C,Xu W.Fast sliding mode control on air-breathing hypersonic vehicles with transient response analysis[J].Proceedings of the Institution of Mechanical Engineers,Part I:Journal of Systems and Control Engineering,2016,230(1):23-34)通過引入輔助誤差變量,將高超聲速飛行器反饋線性化模型轉化為多變量二階模型,設計了非奇異終端滑模面,但控制器中含有符號函數項,會引起系統抖振。為了進一步提高當系統狀態離平衡點較遠時的收斂速率,文獻(Xiaohu Z X W,Gongzhang Z J S.Disturbance compensated terminal sliding mode control for hypersonic vehicles[J].Journal of Beijing University of Aeronautics and Astronautics,2012,11:008)提出了改進型終端滑模面,在平衡點附近由非線性滑模面切換至高增益線性滑模面,不僅避免了奇異問題,且具有較高的收斂速率。
除了奇異問題,抖振現象是限制滑模控制理論在工程應用的關鍵因素。文獻(Feng Y,Yu X,Man Z.Non-singular terminal sliding mode control of rigid manipulators[J].Automatica,2002,38(12):2159-2167)、(Sun H,Li S,Sun C.Finite time integral sliding mode control of hypersonic vehicles[J].Nonlinear Dynamics,2013,73(1-2):229-244)利用邊界層技術,通過飽和函數代替符號函數來削弱系統抖振,但由于系統不確定性或外界擾動存在,在一定程度上降低了控制系統性能,會導致系統存在穩定誤差,使穩態誤差界求取具有一定保守性。在控制系統設計中加入觀測器是一種更加主動和直接的處理系統擾動的方法(Li S,Sun H,Yang J,et al.Continuous finite-time output regulation for disturbed systems under mismatching condition[J].IEEE Transactions on Automatic Control,2015,60(1):277-282),(He S,Lin D,Wang J.Continuous second-order sliding mode based impact angle guidance law[J].Aerospace Science and Technology,2015,41:199-208),(Yang J,Li S,Su J,et al.Continuous nonsingular terminal sliding mode control for systems with mismatched disturbances[J].Automatica,2013,49(7):2287-2291),(Zong Q,Wang J,Tian B,et al.Quasi-continuous high-order sliding mode controller and observer design for flexible hypersonic vehicle[J].Aerospace Science and Technology,2013,27(1):127-137),(Wang F,Zou Q,Hua C,et al.Disturbance observer–based dynamic surface control design for a hypersonic vehicle with input constraints and uncertainty[J].Proceedings of the Institution of Mechanical Engineers,Part I:Journal of Systems and Control Engineering,2016,230(6):522-536),(Wu G,Meng X.Nonlinear disturbance observer based robust backstepping control for a flexible air-breathing hypersonic vehicle[J].Aerospace Science and Technology,2016,54:174-182),(Wang J H,Liu L H,Wang P,et al.Guidance and control system design for hypersonic vehicles in dive phase[J].Aerospace Science and Technology,2016,53:47-60),(Wang J,Wu Y,Dong X.Recursive terminal sliding mode control for hypersonic flight vehicle with sliding mode disturbance observer[J].Nonlinear Dynamics,2015,81(3):1489-1510),(Peng L,Xuefeng P,Jianjun M,et al.Non-homogeneous disturbance observer-based second order sliding mode control for a tailless aircraft[C]//Chinese Automation Congress(CAC),2013.IEEE,2013:120-125)。文獻(Zong Q,Wang J,Tian B,et al.Quasi-continuous high-order sliding mode controller and observer design for flexible hypersonic vehicle[J].Aerospace Science and Technology,2013,27(1):127-137)基于高階滑模觀測器,利用終端滑模理論,設計了擬連續高階滑模控制器,并驗證了方法的有效性,由于滑模面包含積分部分,降低了系統瞬態性能。文獻(Wang F,Zou Q,Hua C,et al.Disturbance observer–based dynamic surface control design for a hypersonic vehicle with input constraints and uncertainty[J].Proceedings of the Institution of Mechanical Engineers,Part I:Journal of Systems and Control Engineering,2016,230(6):522-536),(Wu G,Meng X.Nonlinear disturbance observer based robust backstepping control for a flexible air-breathing hypersonic vehicle[J].Aerospace Science and Technology,2016,54:174-182)提出基于反步法聯合干擾觀測器的高超聲速飛行器控制器設計方法,利用干擾觀測器估計系統未知干擾,提高了系統魯棒性。文獻(Wang J H,Liu L H,Wang P,et al.Guidance and control system design for hypersonic vehicles in dive phase[J].Aerospace Science and Technology,2016,53:47-60)提出了非奇異終端滑模控制方法,采用干擾觀測器估計系統干擾,提高了系統抗擾動性能,降低了滑模控制器增益和削弱了系統抖振。文獻(Wang J,Wu Y,Dong X.Recursive terminal sliding mode control for hypersonic flight vehicle with sliding mode disturbance observer[J].Nonlinear Dynamics,2015,81(3):1489-1510)在提出積分-微分滑模面的基礎上,利用滑模干擾觀測器估計系統外界干擾,設計了遞推滑模控制器,但沒有對整個閉環系統穩定性進行證明。
技術實現要素:
本發明是為了解決現有技術沒有證明觀測器在觀測系統干擾過程中是有界的問題,而提出的一種含干擾觀測器的高超聲速飛行器跟蹤控制方法。
一種含干擾觀測器的高超聲速飛行器跟蹤控制方法以下步驟實現:
步驟一:根據高超聲速飛行器縱向輸入輸出線性化模型,建立帶有系統干擾的二階系統模型;
步驟二:根據步驟一建立的帶有系統干擾的二階系統模型,基于滑模控制理論,設計有限時間終端滑模控制器;
步驟三:對步驟二設計的有限時間終端滑模控制器進行系統穩定性證明。
發明效果:
本發明基于有限時間滑模理論和NHDO設計了快速終端滑模有限時間跟蹤控制器,使得系統滑模面是有限時間穩定的,系統狀態是漸近收斂的。與以上文獻相比,創新之處如下:
(1)本發明對整個閉環系統進行穩定性證明,可保證系統所有狀態在NHDO的收斂階段是有界的。
(2)本發明利用NHDO對系統總干擾進行估計,降低控制器增益,減弱了系統抖振,但沒有犧牲系統的動態性能。與現有技術中滑模面相比,具有更快的收斂速率。
(3)本發明給出的帶有系統干擾的二階系統模型,便于控制器的設計。
附圖說明
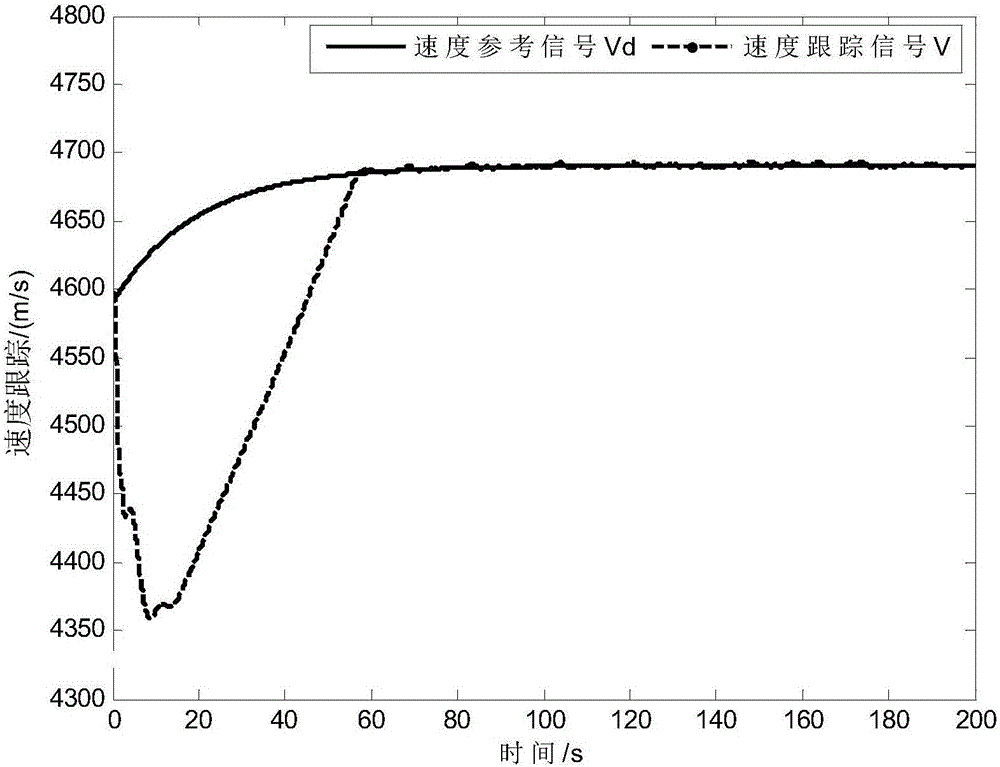
圖1為速度參考指令跟蹤曲線圖;
圖2為速度誤差跟蹤曲線圖;
圖3為高度參考指令跟蹤曲線圖;
圖4為高度誤差跟蹤曲線圖;
圖5為控制輸入φc,δe曲線圖;
圖6為攻角、俯仰角和俯仰角速率曲線圖;
圖7為自適應參數曲線圖;
圖8為系統總干擾估計曲線圖;
圖9為系統干擾估計誤差曲線圖。
具體實施方式
具體實施方式一:一種含干擾觀測器的高超聲速飛行器跟蹤控制方法包括以下步驟:
首先,給出了高超聲速飛行器縱向輸入輸出線性化模型,在此基礎上,建立了帶有系統干擾的二階系統模型。其次,在提出快速非奇異終端滑模的基礎上,基于NHDO對系統干擾進行有效估計,設計了有限時間終端滑模控制器,實現了高超聲速飛行器的快速穩定跟蹤控制。最后,利用李雅普諾夫穩定性理論對整個閉環系統穩定性給出了理論證明,保證系統狀態在NHDO收斂階段是有界的,并對高超聲速縱向非線性模型進行數字仿真,進一步驗證了所設計控制器的有效性。
步驟一:根據高超聲速飛行器縱向輸入輸出線性化模型,建立帶有系統干擾的二階系統模型;
步驟二:根據步驟一建立的帶有系統干擾的二階系統模型,基于滑模控制理論,設計有限時間終端滑模控制器;
步驟三:對步驟二設計的有限時間終端滑模控制器進行系統穩定性證明。
具體實施方式二:本實施方式與具體實施方式一不同的是:所述步驟一中建立帶有系統干擾的二階系統模型具體過程為:
選取文獻(Bolender M A,Doman D B.Nonlinear longitudinal dynamical model of an air-breathing hypersonic vehicle[J].Journal of Spacecraft and Rockets,2007,44(2):374-387)中給出的美國國家航空航天局蘭利研究中心提出的剛性高超聲速飛行器模型如下:
其中V為飛行的速度,h為飛行高度,α為飛行攻角,θ為飛行俯仰角,q為俯仰角速率,φ為發動機節流閥和為節流閥的一階導數;μ為地球引力常數,r=h+RE,RE為地球半徑,γ=θ-α為航跡角,M為控制力矩,Iyy為轉動慣量,g為重力加速度;相關力及力矩系數見文獻(Zhu Z,Xia Y,Fu M.Attitude stabilization of rigid spacecraft with finite‐time convergence[J].International Journal of Robust and Nonlinear Control,2011,21(6):686-702)。
發動機的二階動力學模型如下:
其中φ為發動機節流閥,φc為發動機節流閥設定的指令,ωn為發動機動力學的無阻尼自然頻率,ζ為其阻尼比;
控制輸入u選為[φc δe]T,φc為節流閥設定指令,δe為升降舵偏角指令,系統(1)輸出y選為[V h]T;系統(1)為公式(1)。
為了便于高超聲速飛行器控制系統的設計,采用輸入輸出線性化方法來處理模型,采用文獻(Sun H,Li S,Sun C.Finite time integral sliding mode control of hypersonic vehicles[J].Nonlinear Dynamics,2013,73(1-2):229-244)線性化系統模型。系統(1)線性化模型:
其中,Δfv,Δfh,Δb11,Δb12,Δb21,Δb22是由參數不確定性和外界干擾產生的有界項。令dV=ΔfV+Δb11δe+Δb12φc,dh=Δfh+Δb21δe+Δb22φc;
為了克服對高階系統設計控制器困難的問題,在定義跟蹤誤差變量基礎上,引入輔助誤差變量,其中,Vd(x)、hd(x)分別為期望輸出速度、高度參考指令:
聯合式(4)和式(3)整理成帶有系統干擾的多變量二階系統模型:
其中,
令則式(7)重新寫為:
本發明控制目標:實現高超聲速飛行器輸出速度V和高度h能夠快速穩定跟蹤期望的速度指令Vd和高度指令hd,并同時保證攻角α、俯仰角θ、俯仰角速率q保持在一定的變化范圍內。
相關引理及假設
定義若系統
其中f:U0→Rn是定義在ξ=0的開鄰域U0上的一個連續函數。如果系統在平衡點ξ=0的鄰域U∈U0內是李雅普諾夫穩定的,并且是有限時間穩定的,則系統(9)的平衡點是局部有限時間穩定的。如果f:U=Rn,則系統(9)的平衡點是全局有限時間穩定的。
針對系統(9),假設存在連續可微函數V,并且滿足條件:
(1)V為正定函數。
(2)存在正實數c>0和α∈(0,1),以及一個包含原點的開鄰域使得成立。
則系統是有限時間穩定的,并且收斂時間T滿足其中V0為V的初始值,若U=U0=Rn,則系統為全局有限時間穩定的。
假設1.針對系統(8)干擾d存在且可微Lipschitz常數L=[L1,L2]T,即存在已知正常數L1和L2,分別滿足和
其它步驟及參數與具體實施方式一相同。
具體實施方式三:本實施方式與具體實施方式一或二不同的是:所述步驟二中設計有限時間終端滑模控制器具體過程為:
利用NHDO對系統中的外界擾動和不確定性產生的復合干擾進行有效估計,在此基礎上,基于有限時間滑模控制理論進行控制器設計。能夠保證系統滑模面是有限時間穩定的,輸出跟蹤誤差信號為漸近穩定的。
非齊次干擾觀測器(NHDO)
考慮一階的單輸入單輸出(SISO)非線性系統
其中,x表示系統狀態,它的解是Filippov意義下的解,u∈R為連續的控制輸入,d為充分光滑的不確定函數且m-1次可微,dm-1具有已知的Lipschitz常數L。設計如下NHDO;
式(11)中hi為如下的函數形式
其中,λi>0,μi>0,i=0,1,...,m。
假設系統(10)中的x和u(t)可測量且不存在量測噪聲,所對應的參數λi,μi在逆序上充分大,則系統狀態經歷有限時間的暫態過程后,一定滿足下列方程
z0=x,z1=d,…,zi=vi-1=g(i-1),i=1,…,m (13)
證明:令
對式(14)求導可得
式(15)為Filippov意義下的微分包含,可見包含中未知擾動d和控制輸入u(t)的信息沒有“記憶”。其余證明過程同文獻(Peng L,Xuefeng P,Jianjun M,et al.Non-homogeneous disturbance observer-based second order sliding mode control for a tailless aircraft[C]//Chinese Automation Congress(CAC),2013.IEEE,2013:120-125),證畢。
文獻(Peng L,Xuefeng P,Jianjun M,et al.Non-homogeneous disturbance observer-based second order sliding mode control for a tailless aircraft[C]//Chinese Automation Congress(CAC),2013.IEEE,2013:120-125)中,對于m≤5時給出參數λi和μi的一組有效數值為:λ0=8,λ1=5,λ2=3,λ3=2,λ4=1.5,λ5=1.1,μ0=12,μ1=11,μ2=10,μ3=8,μ4=6,μ5=3。
令則式(8)第二方程重寫為
采用NHDO(17)來估計式(16)中系統干擾di的值。
由命題1可知,NHDO輸出經歷有限時間后收斂于di。
式(17)中觀測器收斂速率取決于L值的大小,L的值越大收斂速率越大,但會引起系統出現瞬態峰值,因此需要折中選取L的值。
基于NHDO的快速非奇異終端滑模控制器設計
為了進一步提高系統收斂速率和增強系統抗擾動性能,本文給出的快速非奇異終端滑模面與文獻(Zhu Z,Xia Y,Fu M.Attitude stabilization of rigid spacecraft with finite‐time convergence[J].International Journal of Robust and Nonlinear Control,2011,21(6):686-702),(Yang L,Yang J.Nonsingular fast terminal sliding‐mode control for nonlinear dynamical systems[J].International Journal of Robust and Nonlinear Control,2011,21(16):1865-1879),(Xu S S D,Chen C C,Wu Z L.Study of nonsingular fast terminal sliding-mode fault-tolerant control[J].IEEE Transactions on Industrial Electronics,2015,62(6):3906-3913)相比具有更快收斂速率。利用NHDO估計系統干擾值的大小,來提高了系統魯棒性,并基于有限時間滑模理論,設計一種新穎的非奇異快速終端滑模控制器。具體過程如下。
選取非奇異終端滑模面:
r1=(2-γ)ηγ-1 (20)
r2=(γ-1)ηγ-2 (21)
其中,i=V,h,1<p/q<2,p和q為正奇數,γ>p/q,β>0,α>0,α0>0;
由于提出的新型快速終端滑模面(18)與文獻(Yu X,Man Z.Model reference adaptive control systems with terminal sliding modes[J].International Journal of Control,1996,64(6):1165-1176)相比能夠避免奇異問題,當時,并利用泰勒公式展開可得
因此,快速非奇異終端滑模面(18)與文獻(Yang L,Yang J.Nonsingular fast terminal sliding‐mode control for nonlinear dynamical systems[J].International Journal of Robust and Nonlinear Control,2011,21(16):1865-1879),(Xu S S D,Chen C C,Wu Z L.Study of nonsingular fast terminal sliding-mode fault-tolerant control[J].IEEE Transactions on Industrial Electronics,2015,62(6):3906-3913)相比具有更快的收斂速率。
對滑模面(18)求導并結合式(8)整理得
其中,
設計終端滑模控制器如下:
其中,k1>0,k2>0、ε>2為非齊次干擾觀測器的輸出。
其它步驟及參數與具體實施方式一或二相同。
具體實施方式四:本實施方式與具體實施方式一至三之一不同的是:所述步驟三中對步驟二設計的有限時間終端滑模控制器進行系統穩定性證明的具體過程為:
對于系統(8),在滿足假設1條件下,選擇快速非奇異終端滑模面(18),在NHDO(17)和控制器(24)-(26)和作用下可得到如下結論。
(1)系統滑模面si是有限時間收斂的;
(2)變量和在有限時間內收斂到零。
證明:對于定理1的證明分為兩步,(i)證明閉環系統狀態在NHDO(17)估計系統干擾過程中是有界的。(ii)證明輔助誤差變量和在有限時間內收斂到零。
(i)下面證明閉環系統狀態在NHDO收斂過程中是有界的
將控制器(24)代入式(22)可得
當時,根據式(23)和式(25)整理得
當時,根據式(23)和式(25)整理得
由式(28)和式(29)整理得
定義輔助變量和如下:
對式(31)求導整理得
選取Lyapunov函數
對(33)沿系統軌線求導得
當時
當時
根據式(35)和式(36),式(34)可整理的
對于參數取值為1<p/q<2和ε>2,則式(34)中設計參數滿足
根據則不等式成立,因此,式(34)可表示為
根據
根據式(40),則式(39)整理得
其中,
由命題1可知,其中Δ為正常數,則式(41)可改寫為
其中,
根據式(42),Δ在有限時間內不會趨于無窮大,因此,整個閉環系統(8)中狀態在非齊次干擾觀測器的收斂階段內是有界的;
證明系統滑模面si在有限時間內收斂到零。
非齊次干擾觀測器經過時間tr滿足因此,式(27)可改寫為
定義輔助變量
對式(44)求導可得
其中,k1>0,k2>0,β>0,矩陣A為赫爾維茨的;
選擇李雅普諾夫函數
V2=ηTPη (46)
其中,P為常值矩陣,滿足黎卡提方程
ATP+PA=-Q (47)
其中,Q=QT>0
對式(46)求導
根據
由式(49)并聯合則式(48)整理得
其中,
當根據式(45)中η在限時間內收斂到零,且收斂時間ts為
其中,V2(tr)在tr時刻的值,由式(44)得到滑模面si在有限時間內收斂到零;
當時,將控制器(24)代入式(8)可得
當t>tr時,對于si>0,對于si<0,因此不是吸引子;則系統滑模面si在有限時間內收斂到零;
系統滑模面si在有限時間內收斂到零,對誤差輔助變量和穩定性分析如下:
當時,則式(18)變為
在有限時間內收斂到
當時,由式(18)可得:
和在區域內有限時間收斂到零;
利用泰勒公式展開可知,
則式(54)可整理為與文獻(Yang L,Yang J.Nonsingular fast terminal sliding‐mode control for nonlinear dynamical systems[J].International Journal of Robust and Nonlinear Control,2011,21(16):1865-1879)滑模面形式類似,因此可參考其證明方法,可得和在tf內收斂到零;
系統(8)在設計的控制器(24)-(26)作用下,誤差輔助變量σ1(x)和σ2(x)在有限時間內的收斂到零,則σV(x)、σh(x)為漸近收斂到零;系統(8)為公式(8)。
變量σ1(x)、σ2(x)在有限時間內收斂到零,則式(5)可寫為
選取李雅普諾夫函數
對式(56)求導
由式(57)可知,和則σV(x)、σh(x)為漸近收斂到零。
其它步驟及參數與具體實施方式一至三之一相同。
實施例一:
為驗證有限時間終端滑模控制器(24)-(26)的有效性。參考文獻(Sun H,Li S,Sun C.Finite time integral sliding mode control of hypersonic vehicles[J].Nonlinear Dynamics,2013,73(1-2):229-244)高超聲速飛行器參數和飛行環境參數見表1,空氣動力學系數取值見表2。
表1飛行器參數和飛行環境參數
表2空氣動力學系數取值
根據上述高超聲速飛行器模型的基本參數可求出高超聲速飛行器的一組平衡工作點。初始值x(0)=[4590.3 33528 0.0334 0.0334 0 0.1802 0]T。在仿真過程中,外界干擾取為d1(t)=0.0024sin(0.2t),d2(t)=0.012sin(0.2t),模型參數不確定性考慮如下:
m=m0(1+Δm),Iyy=I0(1+ΔIyy),
S=S0(1+ΔS),c=c0(1+Δc),
ce=ce0(1+Δce0),ρ=ρ0(1+Δρ), (58)
|Δm|≤0.05,|ΔIyy|≤0.05,|ΔS|≤0.05,
|Δc|≤0.05,|Δρ|≤0.05,|Δce|≤0.05.
其中,m0,I0,S0,c0,ce0,ρ0為對應的標稱值,模型參數不確定性取為Δm=-0.05,ΔIyy=-0.05,Δc=0.05,Δce=0.05,Δρ=0.05,ΔS=0.05。
快速終端滑模的有限時間控制器仿真分析
為了驗證所設計高超聲速飛行器控制策略(24)-(26)的有效性,針對高超聲速飛行器期望速度指令期望速度指令為Vd=4690.3m/s,即ΔV=100m/s,期望高度指令為hd=34528m,即Δh=1000m。觀測器參數取為:λ0=1.1,λ1=1.5,λ2=2,μ0=3,μ1=6,μ2=8。控制參數選取如下:ε=2.1γ=1.8、η=0.01、α0=0.006、α1=0.05、α2=25、k1=0.001、k2=35、p/q=1.2。其仿真結果如圖1-圖9所示。
圖1和圖2為速度V跟蹤曲線;圖3和圖4為高度h跟蹤曲線,從圖1-圖4的仿真結果可得高超聲速飛行器在有限時間終端滑模控制器(24)-(26)作用下能夠實現對參考指令的快速穩定跟蹤,且跟蹤性能較好,滿足跟蹤性能要求。圖5為高超聲速飛行器控制輸入曲線,從仿真曲線可看出系統快速收斂,且控制輸入曲線光滑抖振很小。圖6為高超聲速飛行器其它狀態量的變化曲線,從仿真曲線可看出,攻角α、俯仰角θ和俯仰角速率q在較短的時間內趨于其穩態值。圖7給出了控制器中自適應參數的變化曲線,可以看出,自適應參數快速趨近于穩態值。圖8和圖9給出了有限時間NHDO對擾動估計曲線,從擾動估計曲線可知,NHDO有較快的收斂速度,可以有效消除跟蹤靜差,提高系統精度。
本發明基于有限時間滑模控制理論和NHDO對含有模型參數不確定性以及外界干擾情形下的高超聲速飛行器跟蹤問題進行研究分析。主要結論如下:
(1)基于反饋線性化模型,通過引入誤差輔助變量,給出了帶有系統干擾的多變量二階系統模型,為方便其控制器設計提供了模型基礎。
(2)針對帶有系統干擾的高超聲速飛行器多變量二階系統模型,設計了帶有NHDO的有限時間終端滑模控制器,通過引入了NHDO對復合干擾進行估計,有效降低了控制器增益,避免了通過增大系統增益提高控制系統抗擾動性能。
(3)利用李雅普諾夫理論對所設計的控制器給出了嚴格的理論證明,表明系統狀態在NHDO對系統干擾估計的收斂階段是有界的,并同時能夠使得系統滑模面為有限時間穩定的,速度誤差和高度誤差為漸近穩定的。并對高超聲速飛行器縱向非線性模型進行了數字模擬,進一步驗證了表明了所設計控制器的有效性。
- 還沒有人留言評論。精彩留言會獲得點贊!