本發明涉及飛行器自適應控制技術，具體涉及一種基于LS-SVM的高超聲速飛行器自適應時變預設性能控制方法。

背景技術：

對包含未知非線性動力性的高超聲速飛行器的自適應控制，現有的控制方法基本采用如下兩個步驟進行相關控制系統設計^[1],[2]：

A.借助于神經網絡對任意非線性良好的逼近特性，首先對高超聲速飛行器未知非線性動力學模型進行估計；

B.基于辨識的非線性動力性模型，采用退步控制^[3]、滑模控制^[4]等設計相應的自適應控制方法，實現對高超聲速飛行器的自適應控制。

現有的控制方法雖然能夠實現對高超聲速飛行器的自適應魯棒控制，但是基于神經網絡的自適應控制方法存在以下兩個問題：

首先，基于神經網絡的未知非線性模型逼近算法存在訓練參數多、計算復雜度高、容易陷入局部最優等缺點，因此對于快動態高超聲速飛行器，在線實施可行性較低。因此需要低復雜度的未知非線性模型在線逼近算法。

其次，現有的控制方法只關注在設計的控制器下，高超聲速飛行器控制系統是穩定的，并不關注相應控制系統的瞬態和穩態性能，從而導致高超聲速飛行器控制系統雖然是穩定的，但是容易出現大超調、穩態誤差大等穩態。因此為了實現對高超聲速飛行器的高精度控制和保性能控制，需要新的控制技術來實現飛行器全程預設性能控制。

對于低復雜度的未知非線性模型辨識/逼近算法，基于統計學理論的最小二乘支持向量機(Least Square Support Vector Machine-LS-SVM)機器學習理論由Suykens和Vandewalle提出^[5]，該理論具有小樣本高可信度、全局最優、訓練參數少等優點^[6]，因此適于快動態高超聲速飛行器在線快速辨識未知非線性動力學模型。

對于實現對高超聲速飛行器全飛行過程的保性能控制，為了克服Bechlioulis和Rovithakis⁰提出的固定參數預設性能函數對未知初始狀態/偏差和控制精度上的保守性，需要提出一種新的預設性能函數，從而在保證高超聲速飛行器控制系統穩定性前提下，最大程度上提升系統的瞬態和穩態性能。

參考文獻如下：

[1]Xu B,Shi Z K.An overview on flight dynamics and control approaches for hypersonic vehicles[J].Science China Information Sciences,2015,58(7):1-19.

[2]Xu B.Robust adaptive neural control of flexible hypersonic flight vehicle with dead-zone input nonlinearity[J].Nonlinear Dynamics,2015,80(3):1509-1520.

[3]Chen M,Tao G,Jiang B.Dynamic surface control using neural networks for a class of uncertain nonlinear systems with input saturation[J].IEEE transactions on neural networks and learning systems,2015,26(9):2086-2097.

[4]Xu H,Mirmirani M D,Ioannou P A.Adaptive sliding mode control design for a hypersonic flight vehicle[J].Journal of guidance,control,and dynamics,2004,27(5):829-838.

[5]Suykens J A K,Vandewalle J.Least squares support vector machine classifiers[J].Neural processing letters,1999,9(3):293-300.

[6]Wang Z,Zhang Z,Mao J.Adaptive tracking control based on online LS-SVM identifier[J].International Journal of Fuzzy Systems,2012,14(2):330-336.

[7]Bechlioulis C P,Rovithakis G A.Robust adaptive control of feedback linearizable MIMO nonlinear systems with prescribed performance[J].IEEE Transactions on Automatic Control,2008,53(9):2090-2099.

技術實現要素：

本發明針對傳統高超聲速飛行器自適應控制方法中對未知非線性模型辨識/逼近算法復雜度高且非最優、無法保證全飛行過程保(瞬態/穩態)性能的缺點，提供一種基于LS-SVM的高超聲速飛行器自適應時變預設性能控制方法，本發明在不違背飛器執機構飽和約束條件下，降低對未知非線性動力性學模型在線逼近算法復雜度；同時在保證飛行器控制系統穩定前提下，對高超聲速飛行器的自適應高精度控制。

為達到上述目的，本發明采用如下技術方案：

基于LS-SVM的高超聲速飛行器自適應時變預設性能控制方法，包括如下步驟：

1)根據吸氣式高超聲速飛行器縱向模型設計LS-SVM辨識器與時變預設性能函數，得到誤差轉換模型；

2)根據誤差轉換模型設計速度子系統自適應時變預設性能控制器；

3)根據誤差轉換模型設計高度子系統自適應時變預設性能控制器；

4)根據速度子系統自適應時變預設性能控制器和高度子系統自適應時變預設性能控制器進行穩定性分析和性能分析。

進一步地，步驟1)中所述的吸氣式高超聲速飛行器縱向模型為：

其中，V,h,γ,α,q分別為高超聲速飛行器的速度、高度、航跡角、攻角、俯仰角速度；T,L,D,m,g,M_yy,I_yy為推力、升力、阻力、質量、重力加速度、俯仰力矩、轉動慣量；

將式(1)按照快慢系統分解準則分解成速度子系統A₁和高度子系統A₂：

其中，y_V,y_h分別是速度和高度子系統的輸出；x₁＝γ,x₂＝α+γ,x₃＝q，Φ,δ_e分別為飛行器燃油過量系數和舵偏角，復合非線性函數f_V,f_h1,f_h2為未知非線性函數，采用LS-SVM辨識器進行辨識得到。

進一步地，步驟1)中所述的LS-SVM辨識器輸入層為高超聲速飛行器動力學參數；內積層為高斯核函數，基于LS-SVM理論，得到的速度子系統未知非線性動力性逼近模型為：

其中，分別是辨識樣本、辨識近似函數、待辨識非線性函數、辨識函數權重和辨識基函數，ω為近似誤差，為權重參數，p為偏置誤差；最佳權重參數θ^*由式(4)給出：

其中：S_f,S_X為對應參數可行域。

進一步地，步驟1)中所述的時變預設性能函數為：

其中：e(t)為高超聲速飛行器速度/高度子系統追蹤誤差，其余參數δ₁₀＞δ_1∞＞0，δ₂₀＞δ_2∞＞0，κ₀,κ₁,κ₂＞0都是正的待設計參數；

選擇如下函數：

其中：s(t)是轉換后的誤差，式(6)中函數嚴格單調，且滿足P(0)≠0，因此可得：

式(7)建立原始追蹤誤差e(t)與s(t)之間一一對應關系，通過式(6)與(7)關系，當設計的控制器能夠使得s(t)趨近0，則等價于追蹤誤差e(t)趨近0，s(t)的導數為：

式(8)即為誤差轉換模型。

進一步地，步驟2)具體為：

基于步驟1)中設計的LS-SVM辨識器，對速度子系統A₁進行在線辨識，得到的近似非線性模型為：

其中：是未知最優權重,分別為辨識誤差、辨識誤差的上界以及權重參數二范數上界，為了減少自適應參數維數，取為自適應估計參數，且||·||為2范數；

基于步驟一中設計的時變預設性能函數，速度子系統追蹤誤差的動力學參數模型為：

其中：V_r為參考速度指令；

基于式(10)設計的自適應控制算法為：

自適應律為：

其中：k_V1,k_V2,Γ_V,為待設計正的控制器參數，s_V0為伴隨系統狀態，為了消除控制器飽和，Proj(·)為自適應映射函數。

進一步地，步驟3)具體為：

高度系統控制目的是使得h跟蹤上給定高度指令h_r，高度控制等價于使得航跡角γ跟蹤上γ_d指令，因此高度子系統控制系統設計等價于設計航跡角追蹤控制系統，設計的相應控制器和自適應律如下：

航跡角指令γ_d為：

其中：k_h1,k_h2為待設計參數；s_h為時變預設性能函數下新狀態；Λ_h,δ_h,ε_h,μ_h格式同式(10)，分別是高度系統下的定義的參數；

相應控制器為：

其中：k_γ3,為待設計參數；e_h0,e_h2,e_h3為中間誤差變量，分別是未知非線性參數辨識的最優權重估計值、辨識函數的基函數以及虛擬控制器的微分量；

自適應律為：

其中：Γ_h,為待設計參數。

進一步地，步驟4)具體為：

在步驟2)與3)的速度和高度子系統相應控制器以及自適應律下，相應速度和高度控制系統是穩定的，且對應的控制誤差不變集為：

其中，分別是誤差上界和一個與高度子系統Lyapunov函數相關的正的參數，通過選擇合適的參數即可獲得高精度的速度和高度控制系統。

與現有技術相比，本發明具有以下有益的技術效果：

本發明在不違背飛行器執行機構飽和約束條件下，既可以實現對高超聲速飛行器的全飛行過程穩定控制，又可以保證控制系統的瞬態和穩態性能。其中，借助于LS-SVM理論，對未知非線性動力學模型的辨識/逼近算法中，待設計訓練參數只有兩個，復雜度相比于神經網絡大大減少。

進一步地，本發明可以實現預先設計控制系統的瞬態和穩態性能，且設計的時變預設性能函數具有對初始追蹤誤差不敏感和提升控制系統精度的優點；對于高超聲速飛行器動力學系統存在的未知非線性動力學模型，在線辨識/逼近模型算法結構簡單，待設計訓練參數只有兩個，算法復雜度極大減少；控制器結構簡單，自適應律只有一維，有益于控制算法的在線實施。

附圖說明

圖1為LS-SVM近似未知非線性動力學模型框架圖；

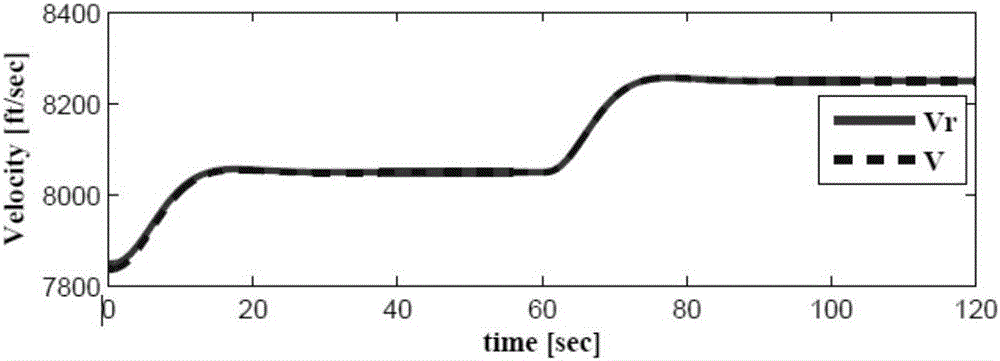
圖2為速度追蹤輸出圖；

圖3為高度追蹤輸出圖；

圖4為燃油輸入圖；

圖5為舵偏輸入圖；

圖6為航跡角追蹤圖；

圖7為攻角輸出圖；

圖8為俯仰角輸出圖；

圖9為速度通道非線性項辨識最優權重輸出圖；

圖10為高度通道非線性項辨識最優權重輸出圖；

圖11為本發明提出的時變預設性能與傳統預設性能控制下速度追蹤誤差圖；

圖12為本發明提出的時變預設性能與傳統預設性能控制下高度追蹤誤差圖。

具體實施方式

為了更好地說明本發明的目的和優點，下面結合附圖和實例對本發明內容做進一步說明：

參見圖1，本發明基于LS-SVM理論，提出高超聲速飛行器自適應時變預設性能控制方法，實現在在滿足執行機構飽和約束和控制系統穩定性前提下，對高超聲速飛行器未知非線性動力性模型進行在線快速辨識/逼近，并實現全飛行過程的保瞬態/穩態性能控制。

本發明針對的吸氣式高超聲速飛行器縱向模型為：

其中：V,h,γ,α,q分別為高超聲速飛行器的速度、高度、航跡角、攻角、俯仰角速度；T,L,D,m,g,M_yy,I_yy為推力、升力、阻力、質量、重力加速度、俯仰力矩、轉動慣量。高超聲速飛行器動力學系統(1)按照快慢系統分解準則，可以分解成速度子系統A₁和高度子系統A₂，為

其中：y_V,y_h分別是速度和高度子系統的輸出；x₁＝γ,x₂＝α+γ,x₃＝q，Φ,δ_e分別為飛行器燃油過量系數和舵偏角。復合非線性函數f_V,f_h1,f_h2為未知非線性函數，需要LS-SVM辨識器進行辨識得到。

步驟一：LS-SVM辨識器與時變預設性能函數設計

基于LS-SVM理論設計的未知非線性動力學模型辨識框架如圖1所示，圖1中輸入層為高超聲速飛行器動力學參數；內積層為高斯核函數；為權重參數，p為偏置誤差。

基于圖1非線性模型逼近圖，得到的速度子系統未知非線性動力性逼近模型為

其中：分別是辨識樣本、辨識近似函數、待辨識非線性函數、辨識函數權重和辨識基函數，ω為近似誤差，T表示向量的轉置。逼近模型(3)中，最佳權重參數θ^*由式(4)給出

其中：S_f,S_X為對應參數可行域。

設計的時變預設性能函數如式(5)所示

其中：e(t)為高超聲速飛行器速度/高度子系統追蹤誤差，其余參數δ₁₀＞δ_1∞＞0，δ₂₀＞δ_2∞＞0，κ₀,κ₁,κ₂＞0都是正的待設計參數。選擇如下函數

其中：s(t)是轉換后的誤差，式(6)中函數嚴格單調，且滿足P(0)≠0，因此可得:

注：式(7)建立原始追蹤誤差e(t)與s(t)之間一一對應關系。通過式(6)與(7)關系，當設計的控制器能夠使得新狀態s(t)趨近0，則等價于追蹤誤差e(t)趨近0。新狀態s(t)的導數為

步驟二：速度子系統自適應時變預設性能控制

基于步驟一中設計的LS-SVM辨識器，對速度子系統A₁進行在線辨識，得到的近似非線性模型為

其中：是未知最優權重,分別為辨識誤差、辨識誤差的上界以及權重參數二范數上界。為了減少自適應參數維數，取為自適應估計參數(||·||為2范數)。

基于步驟一種設計的時變預設性能函數，速度子系統追蹤誤差的動力學參數模型為

其中：V_r為參考速度指令。

基于式(10)設計的自適應控制算法為

自適應律為

其中：k_V1,k_V2,Γ_V,l_V1,為待設計正的控制器參數，s_V0為伴隨系統狀態，為了消除控制器飽和，Proj(·)為自適應映射函數。

步驟三：高度子系統自適應時變預設性能控制

高度系統控制目的是使得h跟蹤上給定高度指令h_r，從式(1)可得，高度控制等價于使得航跡角γ跟蹤上γ_d指令，因此高度子系統控制系統設計等價于設計航跡角追蹤控制系統。同步驟2，設計的相應控制器和自適應律如下：

航跡角指令γ_d為

其中：k_h1,k_h2為待設計參數；s_h為時變預設性能函數下新狀態；Λ_h,δ_h,ε_h,μ_h格式同式(10)，分別是高度系統下的定義的參數。

相應控制器為

其中：k_γ3,l_γ1,為待設計參數；e_h0,e_h2,e_h3為中間誤差變量，分別是未知非線性參數辨識的最優權重估計值、辨識函數的基函數以及虛擬控制器的微分量。

自適應律為

其中：Γ_h,l_γ1,l_γ2為待設計參數。

步驟四：穩定性分析以及性能分析

在步驟二與三的速度和高度子系統相應控制器以及自適應律下，相應速度和高度控制系統是穩定的，且對應的控制誤差不變集為

注：分別是誤差上界和一個與高度子系統Lyapunov函數相關的正的參數，通過選擇合適的參數即可獲得高精度的速度和高度控制系統。

綜合以上控制器設計與分析，可以得到，本發明在不違背飛行器執行機構飽和約束條件下，既可以實現對高超聲速飛行器的全飛行過程穩定控制，又可以保證控制系統的瞬態和穩態性能。其中，借助于LS-SVM理論，對未知非線性動力學模型的辨識/逼近算法中，待設計訓練參數只有兩個，復雜度相比于神經網絡大大減少。

針對高超聲速飛行器縱向動力學模型，仿真參數具體如表1所示：

表1.仿真參數表

初始系統狀態為：V₀＝7850ft/s,h₀＝86000ft,γ₀＝0,q＝0,α＝3.5deg。速度和高度追蹤信號分別為每60s更新且幅值提升量為200ft/s的階躍信號、周期為120s幅值為1000ft的方波信號，二者仿真信號分別由以下濾波器給出

其中，V_c,h_c,S分別是速度指令子系統、高度指令子系統的輸入以及Laplace算子。