本發明屬于多軸數控加工的技術領域，涉及到考慮機床主軸運動誤差與刀具安裝誤差的銑削刀具軸線運動建模問題的研究，具體為一種考慮刀具跳動的多軸銑削刀具軸線建模方法。

背景技術：

在數控加工中，刀具跳動會導致刀具軸線的瞬時位姿偏離理想狀態，改變刀具與工件之間的相對位置關系，引起每齒切厚不均勻，容易產生過切、欠切等現象。刀具跳動無法徹底避免，嚴重地制約了加工精度的進一步提高。在有刀具跳動的情況下，建立刀具軸線運動模型成為了當前研究的熱點問題之一。由于機床主軸、刀柄以及刀具存在制造與安裝的誤差，所以在銑削過程中不可避免地存在刀具回轉軸線與刀具軸線不重合的現象，通常使用若干個位置參數來定義刀具軸線與刀具回轉軸線的相對位置，并描述刀具軸線的運動。

在現有的研究中，并沒有將機床主軸運動誤差與刀具安裝誤差作為研究對象有效地集成。上海交通大學的研究將刀具跳動簡化為包括偏心距ρ、偏心角λ、傾斜角τ和扭轉角φ等參數的模型，并通過實驗數據進行標定。這種方式雖然便于理解和描述刀具跳動現象，但不利于進一步闡明刀具裝夾系統制造、安裝誤差對刀具跳動的耦合作用及物理意義，也不利于建立各誤差因素與刀具跳動的定量、精確關系。

為了解決因機床主軸運動誤差與刀具安裝誤差的銑削刀具軸線運動建模的難題，本發明將主軸動態誤差分析儀金屬標準球的運動軌跡作為銑削刀具軸線運動軌跡，建立了主軸運動誤差與刀具安裝誤差模型，分析了銑削刀具軸線運動的影響，從而得出了刀具軸線運動模型，并使用優化算法標定了模型中未知參數。通過實驗驗證可以看到本文所建立的模型能夠清晰地描述主軸的運動，所提出的參數標定方法具有測量過程簡便，數據處理快速的特點。

技術實現要素：

本發明給出一種主軸運動誤差建模與刀具安裝誤差建模的研究方法。在考慮主軸運動誤差與刀具安裝誤差對銑削刀具軸線運動影響的情況下，解決了刀具軸線運動模型的數學建模問題，并使用粒子群算法對模型中的未知參數進行了標定。本發明所建立的模型能夠清晰地描述主軸的運動，提出的參數標定方法具有測量過程簡便，數據處理快速的特點，并且為抑制刀具跳動和提高加工精度提供了理論基礎，從而在機械加工過程中可以根據該模型對各個零部件所引入的誤差進行分析。

本發明的技術方案為：

本發明首先給出考慮軸承內圈徑向誤差主軸運動模型和刀具安裝誤差模型，并通過建立局部坐標系表示出主軸系統各部件及其誤差，然后采用坐標變換得方法得出主軸運動誤差、刀柄與彈簧夾頭安裝誤差的刀具軸線運動模型。

所述一種考慮刀具跳動的多軸銑削刀具軸線建模方法，其特征在于：包括以下步驟：

步驟1：在多軸立式銑削加工中心前端軸承安裝位置建立坐標系CS1，其中前端軸承孔處圓心為CS1的坐標原點O₁，CS1的X₁、Y₁、Z₁軸分別與機床坐標系CS0的X₀、Y₀、Z₀軸平行；

在坐標系CS1中，建立后端軸承位置處主軸軸心A₁運動軌跡的參數方程為

建立前端軸承位置處主軸軸心A₂運動軌跡的參數方程為

其中，h為前端軸承與后端軸承安裝位置間距，ω為主軸轉速；a₁、a₂、b₁與b₂為描述主軸運動的徑向參數，θ₁、θ₂為描述主軸運動的角度參數；

建立坐標系CS2，取機床主軸底端中心為CS2的坐標原點O₂，主軸軸線方向為CS2的Z₂軸方向，主軸底端平面P₂為CS2的X₂Y₂平面，O₁A₂與A₁A₂兩直線所在平面P₁與平面P₂的交線為CS2的X₂軸，得到坐標系CS2到坐標系CS1的變換矩陣M₂₁為

其中a_2,x，b_2,x，c_2,x是CS2坐標系的X₂軸在坐標系CS1中的方向余弦，a_2,y，b_2,y，c_2,y是CS2坐標系的Y₂軸在坐標系CS1中的方向余弦，a_2,z，b_2,z，c_2,z是CS2坐標系的Z₂軸在坐標系CS1中的方向余弦，與為原點O₂在坐標系CS1中坐標：

l₁為A₁與A₂的間距，l₂為A₂與O₂的間距；

步驟2：在多軸立式銑削加工中心刀柄下端面處建立坐標系CS3，取刀柄下端面中心為CS3的坐標原點O₃，刀柄軸線作為CS3的Z₃軸，CS3的X₃軸、Y₃軸分別平行于CS2軸的X₂軸、Y₂軸，刀柄下端面中心與主軸下端面中心的距離為l₃+Δ₃，其中刀柄下端面中心與主軸下端面中心的設計距離為l₃，Δ₃為刀柄的制造誤差；得到CS3與CS2的變換矩陣M₃₂為：

步驟3：建立坐標系CS4，取多軸立式銑削加工中心彈簧夾頭下端面中心為CS4的原點O₄，彈簧夾頭的下端面為CS4的X₄Y₄平面Π₁，過點O₄且與坐標系CS3的X₃Z₃平面平行的平面為Π₂，Π₁與Π₂的交線為CS4的X₄軸，彈簧夾頭軸線為CS4的Z₄軸；得到坐標系CS4到坐標系CS3的變換矩陣為：

其中a_4,x，b_4,x，c_4,x分別是CS4坐標系的X₄軸在坐標系CS3中的方向余弦，a_4,y，b_4,y，c_4,y分別是CS4坐標系的Y₄軸在坐標系CS3中的方向余弦，a_4,z，b_4,z，c_4,z分別是CS4坐標系的Z₄軸在坐標系CS3中的方向余弦；與為原點O₄在坐標系CS3中坐標；考慮彈簧夾頭的安裝誤差，采用參數ρ₁、φ₁、ρ₂、φ₂，為參數描述原點O₄在CS3下的坐標：

點表示彈簧夾頭上端面中心，l_chuck為彈簧夾頭的長度；

步驟4：沿著彈簧夾頭下端面軸線安裝銑刀，銑刀軸線位于CS4的Z₄軸上，銑刀底部中心距離CS4原點O₄的距離為l_c；建立刀具坐標系CS5，取銑刀底部中心為CS5原點O₅，且CS5的X₅軸、Y₅軸與Z₅軸分別平行與CS4的X₄軸、Y₄軸與Z₄軸；得到CS5到CS4的變換矩陣為：

得到在坐標系CS1下，銑刀底部中心處O₅的運動軌跡為：

與為銑刀底部中心O₅在坐標系CS1中坐標；

步驟5：在多軸立式銑削加工中心上安裝主軸動態誤差分析儀；建立測量坐標系CSM，取測量坐標系CSM的原點為主軸動態誤差分析儀的測量零點，測量坐標系CSM的X_M軸、Y_M軸與Z_M軸分別平行與CS1的X₁軸、Y₁軸與Z₁軸；得到坐標系CS1與坐標系CSM的變換矩陣為：

則主軸動態誤差分析儀測得的第i個測量點m_i在測量坐標系下的坐標表示為

而為CS1的原點在測量坐標系CSM中的坐標，用主軸動態誤差分析儀的測量結果表示為：

其中N_m為主軸動態誤差分析儀的測量點個數，z_s,1為主軸動態誤差分析儀在Z₁軸的安裝位置；

步驟7：等間距選取用參數表示的刀具軸線運動模型所生成的軌跡上的若干點p₁、p₂、…、p_n；然后計算第i個測量點m_i與p₁、p₂、…、p_n的距離，將距離最小值的點選為測量點m_i在軌跡上對應點；取目標函數為

其中m_i(x,y,z)為第i個測量點在坐標系CSM下的坐標，p_k(x,y,z)為測量點m_i在軌跡上對應點坐標系CSM下的坐標；

對目標函數進行優化求解得到刀具軸線運動模型的參數值，進而根據確定的刀具軸線運動模型得到銑刀底部中心O₅和彈簧夾頭下端面中心O₄的運動軌跡，根據O₅和O₄的運動軌跡確定刀具軸線的方向向量。

有益效果

本發明在考慮主軸運動誤差與刀具安裝誤差對銑削刀具軸線運動的影響的情況下，解決了刀具軸線運動模型的數學建模問題。所建立的主軸誤差模型揭示了刀具裝夾系統制造、安裝誤差對刀具跳動的耦合作用規律，建立了各誤差元素與刀具跳動的定量、精確關系，克服了用四個參數描述刀具跳動的缺點。最后，本發明在綜合地考慮這些零部件制造標準之后，使用坐標變換的方法有效的解決了不同零部件安裝誤差模型的難題，清楚的描述了刀具跳動的原因與主軸的運動，為抑制刀具跳動提供了理論基礎和模型。

本發明的附加方面和優點將在下面的描述中部分給出，部分將從下面的描述中變得明顯，或通過本發明的實踐了解到。

附圖說明

本發明的上述和/或附加的方面和優點從結合下面附圖對實施例的描述中將變得明顯和容易理解，其中：

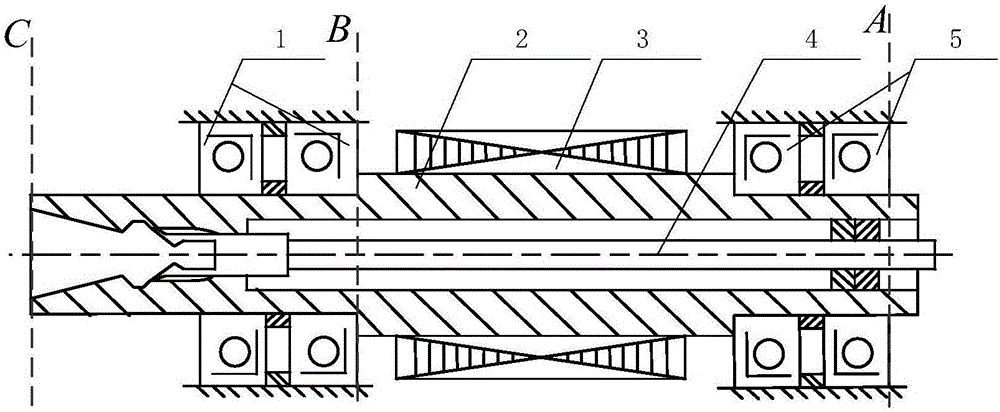
圖1：坐標系CS1與CS2定義示意圖；其中：1.前端軸承 2.軸套 3.旋轉主軸 4.拉釘 5.后端軸承；

圖2：三軸立式銑削加工中心以及坐標系CS1與CS2示意圖；

圖3：坐標系CS2定義示意圖；

圖4：主軸、刀柄、彈簧夾頭、刀具示意圖；

圖5：彈簧夾頭位置以及CS4定義示意圖：(a)彈簧夾頭示意圖(b)CS4定義示意圖；

圖6：參數ρ₁，φ₁，ρ₂，φ₂，定義示意圖；

圖7：目標函數示意圖；

圖8：基于粒子群算法的目標函數收斂示意圖；

圖9：刀具主軸軸線運動示意圖；

圖10：刀具底端中心運動仿真與實驗結果示意圖(Test No.1、Test No.2、Test No.3、Test No.4)；

圖11：刀具軸線運動仿真結果示意圖。

具體實施方式

下面詳細描述本發明的實施例，所述實施例是示例性的，旨在用于解釋本發明，而不能理解為對本發明的限制。

本實施例采用的機床為山東永華YHVT850Z，該機床使用主軸為臺灣羅羿1453448000型主軸，該主軸使用的是P4精度的角接觸軸承。根據標準GB/T 307.2-2005中角接觸軸承的徑向跳動精度，可以確定參數約束條件0≤a₁≤4，0≤b₁≤4，0≤a₂≤4，0≤b₂≤4，(單位：微米)。根據GB/T 25378-2010中彈簧夾頭的制造公差，可以確定參數約束條件0≤ρ₁≤20，0≤ρ₂≤20(單位：微米)。根據GB 10944.1-2006/ISO 7388-1:1983，可以確定-300≤Δ₃≤0(單位：微米)。除了以上約束之外，其他角度位置約束均為[0,2π]。

具體的方法步驟如下：

步驟1：如圖1和圖2所示，在三軸立式銑削加工中心前端軸承安裝位置建立坐標系CS1，其中前端軸承孔處(圖1中B處)圓心為CS1的坐標原點O₁，CS1的X₁、Y₁、Z₁軸分別與機床坐標系CS0的X₀、Y₀、Z₀軸平行；

如圖3所示，后端軸承位置處的主軸軸心為A₁，前端軸承位置處的主軸軸心為A₂，由于軸承內圈存在徑向偏心誤差，所以A₁與A₂會偏離理想位置。在坐標系CS1中，建立后端軸承位置處主軸軸心A₁運動軌跡的參數方程為

建立前端軸承位置處主軸軸心A₂運動軌跡的參數方程為

其中，h為前端軸承與后端軸承安裝位置間距，ω為主軸轉速；a₁、a₂、b₁與b₂為描述主軸運動的徑向參數，θ₁、θ₂為描述主軸運動的角度參數；

在機床主軸底端(圖1中C處)建立坐標系CS2，取機床主軸底端中心為CS2的坐標原點O₂，主軸軸線方向為CS2的Z₂軸方向，主軸底端平面P₂為CS2的X₂Y₂平面，O₁A₂與A₁A₂兩直線所在平面P₁與平面P₂的交線為CS2的X₂軸，顯然通過計算CS2的Z₂軸與X₂軸的外積可以得到CS2的Y₂軸的方向向量；得到坐標系CS2到坐標系CS1的變換矩陣M₂₁為

其中a_2,x，b_2,x，c_2,x是CS2坐標系的X₂軸在坐標系CS1中的方向余弦，a_2,y，b_2,y，c_2,y是CS2坐標系的Y₂軸在坐標系CS1中的方向余弦，a_2,z，b_2,z，c_2,z是CS2坐標系的Z₂軸在坐標系CS1中的方向余弦，與為原點O₂在坐標系CS1中坐標：

l₁為為圖3中A₁與A₂的間距，l₂為為圖3中A₂與O₂的間距；相關數據可以由機床手冊中查閱得到。

步驟2：在三軸立式銑削加工中心刀柄下端面處(圖4D處)建立坐標系CS3，取刀柄下端面中心為CS3的坐標原點O₃，刀柄軸線作為CS3的Z₃軸，CS3的X₃軸、Y₃軸分別平行于CS2軸的X₂軸、Y₂軸，刀柄下端面中心與主軸下端面中心的距離為l₃+Δ₃，其中刀柄下端面中心與主軸下端面中心的設計距離為l₃，Δ₃為刀柄的制造誤差；得到CS3與CS2的變換矩陣M₃₂為：

步驟3：建立坐標系CS4，取三軸立式銑削加工中心彈簧夾頭下端面中心為CS4的原點O₄，彈簧夾頭的下端面為CS4的X₄Y₄平面Π₁(圖4中的E處)，過點O₄且與坐標系CS3的X₃Z₃平面平行的平面為Π₂，Π₁與Π₂的交線為CS4的X₄軸，彈簧夾頭軸線為CS4的Z₄軸；得到坐標系CS4到坐標系CS3的變換矩陣為：

其中a_4,x，b_4,x，c_4,x分別是CS4坐標系的X₄軸在坐標系CS3中的方向余弦，a_4,y，b_4,y，c_4,y分別是CS4坐標系的Y₄軸在坐標系CS3中的方向余弦，a_4,z，b_4,z，c_4,z分別是CS4坐標系的Z₄軸在坐標系CS3中的方向余弦；與為原點O₄在坐標系CS3中坐標；考慮彈簧夾頭的安裝誤差，采用參數ρ₁、φ₁、ρ₂、φ₂，為參數描述原點O₄在CS3下的坐標：

點表示彈簧夾頭上端面中心，l_chuck為彈簧夾頭的長度。

步驟4：沿著彈簧夾頭下端面軸線安裝銑刀，銑刀軸線位于CS4的Z₄軸上，銑刀底部中心距離CS4原點O₄的距離為l_c；建立刀具坐標系CS5，取銑刀底部中心為CS5原點O₅，且CS5的X₅軸、Y₅軸與Z₅軸分別平行與CS4的X₄軸、Y₄軸與Z₄軸；得到CS5到CS4的變換矩陣為：

得到在坐標系CS1下，銑刀底部中心處O₅的運動軌跡為：

與為銑刀底部中心O₅在坐標系CS1中坐標。

步驟5：在三軸立式銑削加工中心上安裝主軸動態誤差分析儀；建立測量坐標系CSM，取測量坐標系CSM的原點為主軸動態誤差分析儀的測量零點，測量坐標系CSM的X_M軸、Y_M軸與Z_M軸分別平行與CS1的X₁軸、Y₁軸與Z₁軸；得到坐標系CS1與坐標系CSM的變換矩陣為：

則主軸動態誤差分析儀測得的第i個測量點m_i在測量坐標系下的坐標表示為

而為CS1的原點在測量坐標系CSM中的坐標，考慮到主軸始終在圍繞CS1的Z₁軸旋轉，最終刀具軸線運動模型所生成的軌跡也應該圍繞CS1的Z₁軸，所以用主軸動態誤差分析儀的測量結果表示為：

其中N_m為主軸動態誤差分析儀的測量點個數，z_s,1為主軸動態誤差分析儀在Z₁軸的安裝位置。

步驟7：等間距選取用參數表示的刀具軸線運動模型所生成的軌跡上的若干點p₁、p₂、…、p_n；然后計算第i個測量點m_i與p₁、p₂、…、p_n的距離，將距離最小值的點選為測量點m_i在軌跡上對應點；取目標函數為

其中m_i(x,y,z)為第i個測量點在坐標系CSM下的坐標，p_k(x,y,z)為測量點m_i在軌跡上對應點坐標系CSM下的坐標；

對目標函數進行優化求解得到刀具軸線運動模型的參數值，進而根據確定的刀具軸線運動模型得到銑刀底部中心O₅和彈簧夾頭下端面中心O₄的運動軌跡，根據O₅和O₄的運動軌跡確定刀具軸線的方向向量。

本發明認為銑削刀具軸線的運動誤差主要來源于主軸軸承、刀柄以及彈簧夾頭的制造誤差，所以可以根據不同零部件的標準給出待標定參數的約束條件。銑削刀具軸線運動建模在本質上是需要對影響其運動的主軸運動參數、刀柄安裝誤差參數、彈簧夾頭安裝誤差參數進行組合優化，最終尋求一組最優的參數，使得銑刀刀具軸線運動軌跡盡可能地逼近測量數據。這里將粒子群算法(PSO)引入到銑削刀具軸線運動模型的參數求解問題中。

本實施例粒子群算法成功地在可行域中尋找到了目標函數最小的參數，從而使得擬合結果逼近測量數據。在本實施例中初始粒子的數目為500，粒子的維數為12。任意粒子x_i所具有的運動速度為每個粒子根據公式

來更新自己的速度和在空間的位置；其中t_step為當前進化的迭代數；r₁與r₂為均勻分布在[0,1]之間的隨機數；c₁與c₂為加速常數，通常設置為2；w為慣性權重，v_i,d為第i個粒子速度向量中的第d個分量，P_best,d為第i個粒子的最有位置向量中第d個分量，G_best,d為群體最優位置向量中的第d個分量，x_i,d為第i個粒子位置向量的第d個分量。在本文中，當連續兩次迭代中對應的目標函數最優值小于10^-15時，算法終止。綜上所述，本發明應用粒子群優化算法后得到的目標函數收斂結果如圖8所示，其中粒子群算法中取初始粒子數為500，最大迭代次數為1000，最大速度為0.4，慣性權重為0.4。

刀具軸線運動模型：刀具軸線的運動實際上能夠形成直紋面，如圖9所示。該直紋面的準線就是O₅與O₄的運動軌跡，母線為直線O₄O₅，令則刀具軸線運動軌跡上任意一點的位置矢量m(s,t)可以表達為下式所示：

m(s,t)＝a(t)+sb(t)

其中0≤t≤2π，0≤s≤1。

根據彈簧夾頭裝夾刀具的誤差不同，本實施例進行了四組主軸動態誤差實驗，將SPN 300型主軸動態誤差分析儀金屬探測球的運動軌跡作為銑削刀具軸線運動軌跡。Test No.1、Test No.2、Test No.3與Test No.4，發明所進行的四個實驗所涉及的機床主軸結構參數、彈簧夾頭制造誤差參數以及刀柄制造誤差參數如表1所示，本文中涉及參數單位的均為微米(um)。

表1機床主軸、彈簧夾頭以及刀柄結構參數表

表2主軸運動誤差與彈簧夾頭的安裝誤差參數的標定結果

盡管上面已經示出和描述了本發明的實施例，可以理解的是，上述實施例是示例性的，不能理解為對本發明的限制，本領域的普通技術人員在不脫離本發明的原理和宗旨的情況下在本發明的范圍內可以對上述實施例進行變化、修改、替換和變型。