本發明涉及一種檢測無線傳感網絡中高維信號重建質量的方法，特別涉及一種在應用迫零估計(ZF)與線性最小均方誤差估計(LMMSE)方法后檢測被重建信號的均方誤差指標的計算方法，屬于無線傳感網絡中信號重建的技術領域。

背景技術：

在無線傳感網絡中的信號重建過程中，隨機范德蒙矩陣扮演著重要的角色。無線傳感器所采集到的信號可以用傅里葉級數展開的形式表示。考慮到每個傳感器所處的地理位置不同，采集到的信號可以表示為一個范德蒙矩陣與一個表示該信號頻譜的向量之間的乘積。考慮到采集信號中的噪聲影響，需要利用估計器對含噪信號進行重建。

經典的算法有迫零估計與最小均方誤差估計，在利用這兩種估計器重建原始信號后，需要對重建的信號計算其均方誤差，從而確定信號重建的準確度。均方誤差的計算需要求解之前提到的范德蒙矩陣的特征值的概率密度函數。

當采集信號的維數、傳感器的個數、以及采集到的信號的帶寬較低時，范德蒙矩陣的特征值的概率密度函數可以通過蒙特卡洛數值計算的方法予以估計。然而，當上述參數值較大時，蒙特卡洛數值計算所需的計算量呈指數增長，因此需要一種能夠簡便又準確地獲得此矩陣特征值的概率密度函數的方法。

技術實現要素：

針對上述問題，本發明所要解決的技術問題是提供一種檢測無線傳感網絡中高維信號重建質量的方法，本發明提供一種能夠簡便又準確地獲得范德蒙矩陣特征值的概率密度函數的方法，從而準確便捷地可以計算出系統的檢測性能指標。

本發明為解決上述技術問題采用以下技術方案：

本發明提供一種檢測無線傳感網絡中高維信號重建質量的方法，所述無線傳感網絡中由m個無線傳感器構成，每個無線傳感器分別采集一個d維的信號，該信號的帶寬表示為n，被采集的信號表示為y＝V^Ha+n_w，其中，y表示信號的測量值，a表示需要被重建的信號，n_w表示白噪聲信號，V表示一個維度為n^d×m的范德蒙矩陣。

當采用迫零估計或最小均方誤差估計方法重建信號時，重建結果的均方誤差分別為和其中，為白噪聲信號的方差，β＝n^d/m，E_λ{·}表示求解關于λ的期望值，λ為矩陣βVV^H的特征值。

通過以下方法求解λ的概率密度函數f_λ(d,β,λ)，具體為：

1)構造優化方程：且滿足條件方程：其中，μ^p為λ的p階矩；

2)通過高斯求積規則把優化方程和條件方程中的積分運算用固定點位置f_λ(d,β,λ)取值的加權和表示出來，即：

其中，λ_j為高斯求積規則中所定義的第j個采樣點的坐標，N為采樣點個數，w_j為對應λ_j的權值；

3)求解優化方程和條件方程，得到對應于λ_j的f_λ(d,β,λ_j)最優值，從而擬合出f_λ(d,β,λ)。

根據得到的f_λ(d,β,λ)即能夠計算重建結果的均方誤差，從而依據均方誤差來衡量采用迫零估計或最小均方誤差估計方法進行信號重建的質量。

作為本發明的進一步技術方案，采用迫零估計方法重建的信號為：

作為本發明的進一步技術方案，采用最小均方誤差估計方法重建的信號為：其中，I表示單位矩陣。

作為本發明的進一步技術方案，范德蒙矩陣V的元素為：其中，V_s,t表示V的第s行第t列元素，x_t表示第t個無線傳感器的地理位置。

作為本發明的進一步技術方案，a是一個n^d維向量。

作為本發明的進一步技術方案，y是一個m維向量。

本發明采用以上技術方案與現有技術相比，具有以下技術效果：當采集信號的維數、傳感器的個數以及采集到的信號的帶寬值較大時，采用本發明的技術方案能夠簡便又準確地獲得范德蒙矩陣特征值的概率密度函數。

附圖說明

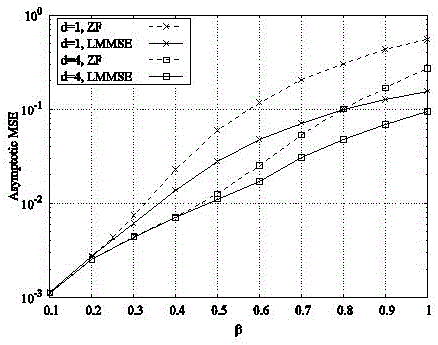
圖1是本發明具體實施例中計算得出的系統均方誤差的數值圖。

具體實施方式

下面結合附圖以及具體實施例對本發明的技術方案做進一步的詳細說明：

在一個由m個無線傳感器構成的無線傳感網絡中，每個傳感器負責采集一個d維的信號，該信號的帶寬表示為n。被采集的信號可以用需要被重建的信號表示為：y＝V^Ha+n_w，其中，y表示信號的測量值，是一個m維向量；a表示需要被重建的信號，是一個n^d維向量；n_w表示白噪聲信號；V表示一個維度為n^d×m的范德蒙矩陣，此矩陣的第s行第t列元素可以表示為：其中，x_t表示第t個無線傳感器的地理位置。

當應用迫零估計(ZF)時，重建的信號表示為：該重建結果的均方誤差因此可以寫為：

當應用最小均方誤差估計(LMMSE)時，重建的信號表示為：該重建結果的均方誤差因此可以寫為：其中，I表示單位矩陣。

當m、n、d的值較大時，假設n^d與m的比值表示為β＝n^d/m，則應用迫零估計或最小均方誤差估計重建信號的均方誤差可以進一步被準確估計為：

其中，λ為矩陣βVV^H的特征值。因此，λ的概率密度函數(PDF)f_λ(d,β,λ)需要一種方法予以給出，其中，d與β為其兩個參數。

在計算λ的概率密度函數(PDF)之前，λ的p階矩已知，記為μ^p。λ的p階矩在A.Nordio,C.-F.Chiasserini,E.Viterbo,“Performance of linear field reconstruction techniques with noise and uncertain sensor locations,”IEEE Trans.on Signal Processing,Vol.56,No.8,pp.3535–3547,Aug.2008.中有詳細介紹。

構造優化方程：且滿足條件方程：

通過高斯求積規則把優化方程和條件方程中的積分運算用固定點位置f_λ(d,β,λ)取值的加權和表示出來，即：其中，λ_j為高斯求積規則中所定義的第j個采樣點的坐標，N為采樣點個數，w_j為對應λ_j的權值，也通過高斯求積規則獲得。因此，通過求解優化方程和條件方程，對應于每個λ_j采樣點的f_λ(d,β,λ_j)最優值可以被求出，從而擬合得到f_λ(d,β,λ)。

在仿真測試環境中，我們測試當d＝1或4、且m＝n^d/β的參數設置，對應于特征值λ的前12階矩均已知。假設系統分別采用迫零估計與最小均方誤差估計方法重建信號，我們分別比較由蒙特卡洛方法得出的系統均方誤差與由本發明所提出的方法所計算出的系統均方誤差。

如圖1所示的系統均方誤差的數值圖，通過觀察圖1可以看出，最小均方誤差估計方法的表現強于迫零估計方法，因為最小均方誤差的目標即是最小化均方誤差。更重要的是，隨著β值得增大，由本發明計算出的均方誤差與蒙特卡洛方法得出的均方誤差結果非常相近。但是本發明使得均方誤差的計算量大大縮小，圖1中，“□”和“×”的點表示蒙特卡洛方法得出的仿真結果，虛線和實線的線條表示的是本發明方法的仿真結果。

以上所述，僅為本發明中的具體實施方式，但本發明的保護范圍并不局限于此，任何熟悉該技術的人在本發明所揭露的技術范圍內，可理解想到的變換或替換，都應涵蓋在本發明的包含范圍之內，因此，本發明的保護范圍應該以權利要求書的保護范圍為準。