本發明涉及計算機技術領域，尤其涉及一種高爐風口回旋區深度計算方法及系統。

背景技術：

高爐是一個復雜的逆流式反應器，從高爐下部吹進的高溫高壓的熱風，在風口回旋區與焦炭發生燃燒反應，產生煤氣流。煤氣流在上升過程中，與高爐上部加入的礦石之間進行能量交換，發生還原反應，生成鐵水和爐渣。風口回旋區是高爐穩定操作不可缺少的重要反應區，高爐風口回旋區的深度和反應情況，直接影響著高爐煤氣分布、爐料下降以及整個高爐的傳熱傳質過程。

現有技術中，一般是采用歐拉模型建立風口回旋區的機理模型，然后利用機理模型，計算不同條件下的風口回旋區深度。

然而，采用現有的采用機理模型來計算回旋區深度的方法中，模型需要的參數和條件較多，比如爐壁的近壁區域使用標準壁面函數、噴煤參數、死料柱表面使用壁面條件等，使得計算復雜，并且該方法的計算時間較長，導致效率低下。

可見，現有技術中的高爐風口回旋區深度的計算方法，存在實現復雜、效率低的技術問題。

技術實現要素：

本發明提供一種高爐風口回旋區深度的計算方法及系統，用以解決現有技術中高爐風口回旋區深度計算方法的實現復雜、效率低的技術問題。

第一方面，本發明實施例提供了一種高爐風口回旋區深度計算方法，包括：獲取利用歐拉模型得到的回旋區深度的計算結果；根據所述計算結果，獲得所述回旋區深度的變化規律；根據所述變化規律，獲取與所述回旋區深度相關的參數，所述參數包括爐腹煤氣密度、焦炭密度、風口前焦炭粒度、煤氣體積流率、風口總面積、回旋區煤氣溫度和熱風壓力；根據所述參數，構建所述回旋區深度的計算模型，所述計算模型為：其中，D_R為回旋區深度，ρ_o為爐腹煤氣密度，ρ_s為焦炭密度，D_P為風口前焦炭粒度，V_g為煤氣體積流率，S_T為風口總面積，T_r回旋區煤氣溫度，P_b熱風壓力。

可選的，所述獲取利用歐拉模型得到的回旋區深度的計算結果，包括：根據歐拉模型，構建所述回旋區深度的機理模型，所述機理模型具體為：

其中，k為湍動能，ε為湍動能耗散率，G_k表示由層流速度梯度而產生的湍流動能，G_b為浮力產生的湍流動能，Y_M為在可壓縮湍流中，過渡的擴散產生的波動，σ_k和σ_ε是k方程和ε方程的湍流Prandtl數，式中C_1ε＝1.44，C_2ε＝1.92，C_3ε＝0.09，C_μ＝0.09，σ_k＝1.0，σ_ε＝1.3，S_k和S_ε為常數；確定所述機理模型的邊界條件，所述邊界條件包括爐壁的近壁區域使用標準壁面函數、風口處設置速度入口邊界、模型上部出口處設定壓力出口條件、模型對稱的兩側面使用周期循環邊界和死料柱表面使用壁面條件；根據所述機理模型和所述邊界條件，獲得回旋區深度的計算結果。

可選的，根據所述參數，構建所述回旋區深度的計算模型，包括：獲取回旋區的受力情況；獲得所述參數；根據所述受力情況和所述參數，計算所述回旋區的穿透系數，所述穿透系數為根據所述穿透系數，擬合得到所述回旋區深度的計算模型。

可選的，所述回旋區煤氣溫度為一固定值。

可選的，所述爐腹煤氣密度為煤氣中各組分的分子量所占的百分比。

第二方面，本發明實施例提供了一種高爐風口回旋區深度計算系統，包括：第一獲取模塊，用于獲取利用歐拉模型得到的回旋區深度的計算結果；獲得模塊，用于根據所述計算結果，獲得所述回旋區深度的變化規律；第二獲取模塊，用于根據所述變化規律，獲取與所述回旋區深度相關的參數，所述參數包括爐腹煤氣密度、焦炭密度、風口前焦炭粒度、煤氣體積流率、風口總面積、回旋區煤氣溫度和熱風壓力；構建模塊，用于根據所述參數，構建所述回旋區深度的計算模型，所述計算模型為：其中，式(1)中，D_R為回旋區深度，單位為m，ρ_o為爐腹煤氣密度，單位為kg/m³，ρ_s為焦炭密度，單位為kg/m³，D_P為風口前焦炭粒度，單位為m，V_g為煤氣體積流率，單位為m³/s，S_T為風口總面積，單位為m²，T_r回旋區煤氣溫度，單位為℃，P_b熱風壓力，單位為MPa。

可選的，所述第一獲取模塊包括：構建單元，用于根據歐拉模型，構建所述回旋區深度的機理模型，所述機理模型具體為：

其中，k為湍動能，ε為湍動能耗散率，G_k表示由層流速度梯度而產生的湍流動能，G_b為浮力產生的湍流動能，Y_M為在可壓縮湍流中，過渡的擴散產生的波動，σ_k和σ_ε是k方程和ε方程的湍流Prandtl數，式中C_1ε＝1.44，C_2ε＝1.92，C_3ε＝0.09，C_μ＝0.09，σ_k＝1.0，σ_ε＝1.3，S_k和S_ε為常數；確定單元，用于確定所述機理模型的邊界條件，所述邊界條件包括爐壁的近壁區域使用標準壁面函數、風口處設置速度入口邊界、模型上部出口處設定壓力出口條件、模型對稱的兩側面使用周期循環邊界和死料柱表面使用壁面條件；第一處理單元，用于根據所述機理模型和所述邊界條件，得出回旋區深度的計算結果。

可選的，所述構建模塊包括：第一獲取單元，用于獲取回旋區的受力情況；獲得單元，用于獲得所述參數；第二處理單元，用于根據所述受力情況和所述參數，計算所述回旋區的穿透系數，所述穿透系數為第三處理單元，用于根據所述穿透系數，擬合得到所述回旋區深度的計算模型。

可選的，所述回旋區煤氣溫度為一固定值。

可選的，所述爐腹煤氣密度為煤氣中各組分的分子量所占的百分比。

本發明實施例中提供的一個或多個技術方案，至少具有如下技術效果或優點：

1、本申請實施例提供的方法，利用歐拉模型得到的回旋結果獲得所述回旋區深度的變化規律，并根據所述變化規律，獲取與所述回旋區深度相關的參數，再根據所述參數，構建所述回旋區深度的計算模型，從而計算出回旋區深度，利用較少的參數可以計算得到回旋區深度，解決了現有的利用歐拉模型計算方法的實現復雜和效率低的問題，大大簡化了回旋區深度計算的復雜性，并減少了計算時間，提高了計算效率。

2、本申請實施例提供的系統，構建模塊可利用第二獲取模塊根據變化規律獲取的參數，構建所述回旋區深度的計算模型，從而計算出回旋區深度，利用較少的參數可以計算得到回旋區深度，解決了現有的利用歐拉模型計算方法的實現復雜和效率低的問題，大大簡化了回旋區深度計算的復雜性，并減少了計算時間，提高了計算效率。

上述說明僅是本發明技術方案的概述，為了能夠更清楚了解本發明的技術手段，而可依照說明書的內容予以實施，并且為了讓本發明的上述和其它目的、特征和優點能夠更明顯易懂，以下特舉本發明的具體實施方式。

附圖說明

為了更清楚地說明本發明實施例或現有技術中的技術方案，下面將對實施例或現有技術描述中所需要使用的附圖作一簡單地介紹，顯而易見地，下面描述中的附圖是本發明的一些實施例，對于本領域普通技術人員來講，在不付出創造性勞動的前提下，還可以根據這些附圖獲得其他的附圖。

圖1為本發明實施例中深度計算方法的流程圖；

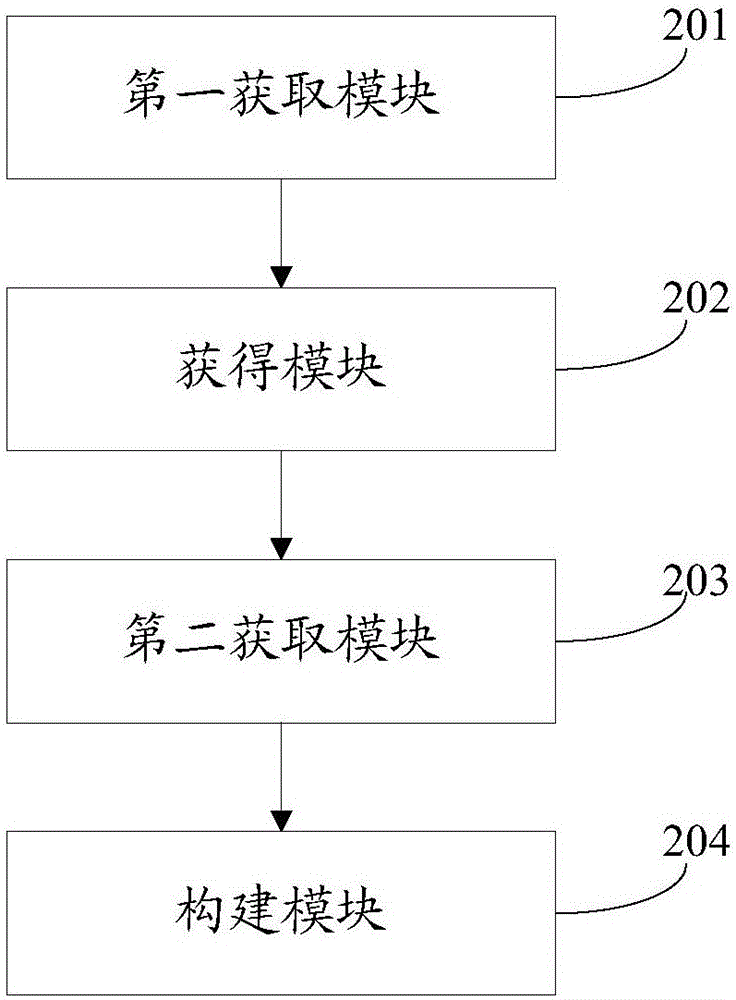
圖2為本發明實施例中深度計算系統的邏輯結構示意圖。

具體實施方式

本發明提供一種高爐風口回旋區深度的計算方法及系統，解決了現有技術中高爐風口回旋區深度計算方法的實現復雜、效率低的技術問題。降低了回旋區深度計算的復雜性、并提高了回旋區深度計算的效率。

本申請實施例中的技術方案，總體思路如下：

一種高爐風口回旋區深度計算方法，包括：獲取利用歐拉模型得到的回旋區深度的計算結果；根據所述計算結果，獲得所述回旋區深度的變化規律；根據所述變化規律，獲取與所述回旋區深度相關的參數，所述參數包括爐腹煤氣密度、焦炭密度、風口前焦炭粒度、煤氣體積流率、風口總面積、回旋區煤氣溫度和熱風壓力；根據所述參數，構建所述回旋區深度的計算模型，所述計算模型為：其中，D_R為回旋區深度，ρ_o為爐腹煤氣密度，ρ_s為焦炭密度，D_P為風口前焦炭粒度，V_g為煤氣體積流率，S_T為風口總面積，T_r回旋區煤氣溫度，P_b熱風壓力。

上述方法通過利用歐拉模型得到的回旋區深度的計算結果找出所述回旋區深度的變化規律，并根據該變化規律，獲取與所述回旋區深度相關的參數，并以上述參數構建回旋區深度的計算模型，從而計算出回旋區深度，利用較少的參數可以計算得到回旋區深度，解決了現有的利用歐拉模型計算方法的實現復雜和效率低的問題，大大簡化了回旋區深度計算的復雜性，并減少了計算時間，提高了計算效率。

為使本發明實施例的目的、技術方案和優點更加清楚，下面將結合本發明實施例中的附圖，對本發明實施例中的技術方案進行清楚、完整地描述，顯然，所描述的實施例是本發明一部分實施例，而不是全部的實施例。基于本發明中的實施例，本領域普通技術人員在沒有作出創造性勞動前提下所獲得的所有其他實施例，都屬于本發明保護的范圍。

實施例一

本實施例提供一種高爐風口回旋區深度計算方法，請參考圖1，所述方法包括：

步驟S101，獲取利用歐拉模型得到的回旋區深度的計算結果；

步驟S102，根據所述計算結果，獲得所述回旋區深度的變化規律；

步驟S103，根據所述變化規律，獲取與所述回旋區深度相關的參數，所述參數包括爐腹煤氣密度、焦炭密度、風口前焦炭粒度、煤氣體積流率、風口總面積、回旋區煤氣溫度和熱風壓力；

步驟S104，根據所述參數，構建所述回旋區深度的計算模型，所述計算模型為：其中，D_R為回旋區深度，ρ_o為爐腹煤氣密度，ρ_s為焦炭密度，D_P為風口前焦炭粒度，V_g為煤氣體積流率，S_T為風口總面積，T_r回旋區煤氣溫度，P_b熱風壓力。

下面，結合圖1對本申請提供的回旋區深度計算方法進行詳細介紹：

首先，執行步驟S101，獲取利用歐拉模型得到的回旋區深度的計算結果。

在本申請實施例中，歐拉模型是Fluent中最復雜的多相流模型，它建立了一套包含有n個的動量方程和連續方程來求解每一相，可以利用歐拉模型來求解回旋區深度，具體地，可以通過構建歐拉模型，然后通過計算機計算，然而利用歐拉模型來計算回旋區深度的方法中，由于該模型中包含了大量的參數和方程，求解相當復雜，一般求解過程需要20多個小時或者更長，因此計算效率很低，不能適用于實際生產中，因此，本申請基于此，在歐拉模型求解的基礎上，進行一進步優化。

再下來，執行步驟S102，根據所述計算結果，獲得所述回旋區深度的變化規律。

在具體實施過程中，可以在計算機中根據得出的計算結果，人工分析上述計算結果，并可以利用相關軟件進行分析，例如MATLAB，從而獲得回旋區深度的變化規律。

接下來，執行步驟S103，根據所述變化規律，獲取與所述回旋區深度相關的參數，所述參數包括爐腹煤氣密度、焦炭密度、風口前焦炭粒度、煤氣體積流率、風口總面積、回旋區煤氣溫度和熱風壓力。

在具體實施過程中，根據回旋區深度的變化規律，找出與回旋區深度相關的主要參數。

最后，執行步驟S104，根據所述參數，構建所述回旋區深度的計算模型，所述計算模型為：其中，D_R為回旋區深度，ρ_o為爐腹煤氣密度，ρ_s為焦炭密度，D_P為風口前焦炭粒度，V_g為煤氣體積流率，S_T為風口總面積，T_r回旋區煤氣溫度，P_b熱風壓力。

在具體實施過程中，可以利用MATLAB在計算機中進行擬合，從而確定各項系數。并將得出的計算模型的結果與理論值進行比較，得出風口回旋區形貌。

從上述技術方案中，可以看出本實施例中提供的方法通過利用歐拉模型得到的回旋區深度的計算結果找出所述回旋區深度的變化規律，并根據該變化規律，獲取與所述回旋區深度相關的參數，并以上述參數構建回旋區深度的計算模型，從而計算出回旋區深度，利用較少的參數可以計算得到回旋區深度，解決了現有的利用歐拉模型計算方法的實現復雜和效率低的問題，大大簡化了回旋區深度計算的復雜性，并減少了計算時間，提高了計算效率。

可選的，所述獲取利用歐拉模型得到的回旋區深度的計算結果，包括：

根據歐拉模型，構建所述回旋區深度的機理模型，所述機理模型具體為：

其中，k為湍動能，ε為湍動能耗散率，G_k表示由層流速度梯度而產生的湍流動能，G_b為浮力產生的湍流動能，Y_M為在可壓縮湍流中，過渡的擴散產生的波動，σ_k和σ_ε是k方程和ε方程的湍流Prandtl數，式中C_1ε＝1.44，C_2ε＝1.92，C_3ε＝0.09，C_μ＝0.09，σ_k＝1.0，σ_ε＝1.3，S_k和S_ε為常數，用戶可以根據實際情況設置；

確定所述機理模型的邊界條件，所述邊界條件包括爐壁的近壁區域使用標準壁面函數、風口處設置速度入口邊界、模型上部出口處設定壓力出口條件、模型對稱的兩側面使用周期循環邊界和死料柱表面使用壁面條件；

根據所述機理模型和所述邊界條件，獲得回旋區深度的計算結果。

具體來說，假設風口回旋區內的流動是不存在燃燒的等溫流過程。所以計算過程中只有連續方程和動量守恒方程而不再考慮能量守恒方程。

質量守恒方程方程形式為：

氣相：

固相：

該方程是質量守恒的一般式，它適用于可壓縮和不可壓縮流體。其中，ρ是密度，t是時間，υ是速度矢量，Sm是加入到連續相的質量。也可以是其他自定義的源項。動量守恒其本質是牛頓第二定律。該定律可以表述為：微元體中流體的動量對時間的變化率等于外界作用在該微元體上的各種力之和。按照這一定律，可以得出在慣性坐標系中的動量守恒方程。

氣相：

固相：

式中p是流體微元體上的壓力(靜壓)，g代表作用在微元體上的重力體積力。并由此得到標準k-ε湍流模型，需要說明的是，最簡單完整的湍流模型具有兩個基本方程，有兩個變量(速度和長度尺度)需要求解。標準k-ε模型是基于湍流動能和擴散率，k方程為精確方程，ε方程式通過經驗公式推導而來的。在求解上述標準k-ε模型時，把氣相與顆粒相都看成共同存在于計算域內的擬均相連續介質，各相使用體積分數區分。每一相的質量和動量守恒方程在歐拉框架下求解。空間離散格式使用一階迎風格式，離散方程組使用壓力速度耦合的SIMPLE(Semi-Implicit Method for Pressure-Linked Equations)方法求解,湍流流動使用k-ε雙方程模型計算。

可選的，根據所述參數，構建所述回旋區深度的計算模型，包括：

獲取回旋區的受力情況；

獲得所述參數；

根據所述受力情況和所述參數，計算所述回旋區的穿透系數，所述穿透系數為

根據所述穿透系數，擬合得到所述回旋區深度的計算模型。

具體來說，假設回旋區邊界上一點只受到熱風沖力和焦炭對熱風氣流的阻力，對其受力進行分析，并以理論燃燒溫度代替送風溫度、回旋區邊界前焦炭粒徑作為有效直徑，回旋區受力情況主要包括熱風穿透力、焦炭重力和回旋區壁(即死料柱焦炭層)的反力，然后根據該受力情況和前述獲得的相關參數，計算所述回旋區的穿透系數最后，通過擬合確定系數，得到最終的回旋區深度的計算模型。

關于計算模型中的相關參數，所述爐腹煤氣密度為煤氣中各組分的分子量所占的百分比，所述回旋區煤氣溫度為一固定值。ρ_s為焦炭密度，為一常數；V_g為煤氣體積流率，根據高爐熱風量得到，隨送風制度變化可以做相應的調整；S_T為風口總面積，根據送風制度而確定；將各參數帶入計算模型中計算可以得到風口回旋區深度，

基于同一發明構思，本發明實施例還提供了實施例一中方法對應的系統，見實施例二。

實施例二

本實施例提供了一種高爐風口回旋區深度計算系統，請參考圖2，所述系統包括：

第一獲取模塊201，用于獲取利用歐拉模型得到的回旋區深度的計算結果；

獲得模塊202，用于根據所述計算結果，獲得所述回旋區深度的變化規律；

第二獲取模塊203，用于根據所述變化規律，獲取與所述回旋區深度相關的參數，所述參數包括爐腹煤氣密度、焦炭密度、風口前焦炭粒度、煤氣體積流率、風口總面積、回旋區煤氣溫度和熱風壓力；

構建模塊204，用于根據所述參數，構建所述回旋區深度的計算模型，所述計算模型為：

其中，式(1)中，D_R為回旋區深度，單位為m，ρ_o為爐腹煤氣密度，單位為kg/m³，ρ_s為焦炭密度，單位為kg/m³，D_P為風口前焦炭粒度，單位為m，V_g為煤氣體積流率，單位為m³/s，S_T為風口總面積，單位為m²，T_r回旋區煤氣溫度，單位為℃，P_b熱風壓力，單位為MPa。

本實施例提供的一種高爐風口回旋區深度計算系統中，所述第一獲取模塊包括：

構建單元，用于根據歐拉模型，構建所述回旋區深度的機理模型，所述機理模型具體為：

其中，k為湍動能，ε為湍動能耗散率，G_k表示由層流速度梯度而產生的湍流動能，G_b為浮力產生的湍流動能，Y_M為在可壓縮湍流中，過渡的擴散產生的波動，σ_k和σ_ε是k方程和ε方程的湍流Prandtl數，式中C_1ε＝1.44，C_2ε＝1.92，C_3ε＝0.09，C_μ＝0.09，σ_k＝1.0，σ_ε＝1.3，S_k和S_ε為常數；

確定單元，用于確定所述機理模型的邊界條件，所述邊界條件包括爐壁的近壁區域使用標準壁面函數、風口處設置速度入口邊界、模型上部出口處設定壓力出口條件、模型對稱的兩側面使用周期循環邊界和死料柱表面使用壁面條件；

第一處理單元，用于根據所述機理模型和所述邊界條件，得出回旋區深度的計算結果。

本實施例提供的一種高爐風口回旋區深度計算系統中，所述構建模塊包括：

第一獲取單元，用于獲取回旋區的受力情況；

獲得單元，用于獲得所述參數；

第二處理單元，用于根據所述受力情況和所述參數，計算所述回旋區的穿透系數，所述穿透系數為

第三處理單元，用于根據所述穿透系數，擬合得到所述回旋區深度的計算模型。

本實施例提供的一種高爐風口回旋區深度計算系統中，所述回旋區煤氣溫度為一固定值。

本實施例提供的一種高爐風口回旋區深度計算系統中，所述爐腹煤氣密度為煤氣中各組分的分子量所占的百分比。

由于本發明實施例二所介紹的系統，為實施本發明實施例一的高爐風口回旋區深度計算方法所采用的系統，故而基于本發明實施例一所介紹的方法，本領域所屬人員能夠了解該系統的具體結構及變形，故而在此不再贅述。凡是本發明實施例一的方法所采用的系統都屬于本發明所欲保護的范圍。

本申請實施例中提供的技術方案，至少具有如下技術效果或優點：

本發明實施例中提供的一個或多個技術方案，至少具有如下技術效果或優點：

1、本申請實施例提供的方法，利用歐拉模型得到的回旋結果獲得所述回旋區深度的變化規律，并根據所述變化規律，獲取與所述回旋區深度相關的參數，再根據所述參數，構建所述回旋區深度的計算模型，從而計算出回旋區深度，利用較少的參數可以計算得到回旋區深度，解決了現有的利用歐拉模型計算方法的實現復雜和效率低的問題，大大簡化了回旋區深度計算的復雜性，并減少了計算時間，提高了計算效率。

2、本申請實施例提供的系統，構建模塊可利用第二獲取模塊根據變化規律獲取的參數，構建所述回旋區深度的計算模型，從而計算出回旋區深度，利用較少的參數可以計算得到回旋區深度，解決了現有的利用歐拉模型計算方法的實現復雜和效率低的問題，大大簡化了回旋區深度計算的復雜性，并減少了計算時間，提高了計算效率。

盡管已描述了本發明的優選實施例，但本領域內的技術人員一旦得知了基本創造性概念，則可對這些實施例作出另外的變更和修改。所以，所附權利要求意欲解釋為包括優選實施例以及落入本發明范圍的所有變更和修改。

顯然，本領域的技術人員可以對本發明實施例進行各種改動和變型而不脫離本發明實施例的精神和范圍。這樣，倘若本發明實施例的這些修改和變型屬于本發明權利要求及其等同技術的范圍之內，則本發明也意圖包含這些改動和變型在內。