本發明涉及刑偵與警務研判、警情數據挖掘、公共安全、犯罪地理學技術領域，尤其涉及一種系列犯罪案件地理目標預測方法。

背景技術：

犯罪都是在一定的時空和一定的受害人與犯罪人之間完成的，羅斯莫博士(rossmo)通過將犯罪現場的犯罪活動和空間行為的地理知覺聯系起來，在距離遞減模式原理的基礎上，提出了犯罪地理目標模型，并編成計算機程序，同時用多起案件加以驗證，獲得了很大的成功。1994年ecri(environmentalcriminologyresearchinc，環境犯罪研究有限公司)正式成立，成功設計了參宿七(rigel)軟件，使其服務于犯罪偵查。目前，北美和歐洲信息化較高的警察機構都在使用參宿七軟件。2005年以來，國內學者和專家陸續對犯罪地理畫像理論及國外應用案例進行了研究，同時伴隨著我國警務部門對警務地理信息系統的全面建設，使其在我國具有極大應用前景。

隨著地理畫像技術的發展，警務部門越來越重視其在偵破案件方面的作用。地理畫像中的犯罪地理目標模型(criminalgeographicprofiling，cgt)已在國內外警務部門進行了實際應用，如系列殺人、系列入室盜竊、系列街頭盜竊、系列搶劫、系列強奸、系列縱火等系列案件，均獲得了較好的預測效果。目前，雖然在地理畫像領域取得了一些研究與應用成果，但是也存在著少許不足，如：原有的cgt模型僅基于案件點空間信息(作案地點之間的相互距離)進行預測，忽略了交通環境(只包括道路的條數，選擇逃跑路線用)、警務監督等多種因素對嫌疑人選擇落腳點的影響，缺乏對嫌疑人落腳點選擇機理研究，導致模型預測精度不高、或預測失敗等問題。雖然已有文獻對犯罪地理目標模型進行了改進，但其僅考慮了地理因素(作案地點之間的相互距離)而沒有考慮其它因素，導致預測不準確。

技術實現要素：

1.發明要解決的技術問題

針對現有技術的犯罪地理目標模型存在預測不準確的問題，本發明提供了一種系列犯罪案件地理目標預測方法。它可以取得比較好的預測效果，預測命中百分率至少高于原始cgt模型6％以上。

2.技術方案

為解決上述問題，本發明提供的技術方案為：

一種系列犯罪案件地理目標預測方法：

a、模型計算區域的確定

對連環案件進行區域劃分后，依據犯罪分子有效案件點的分布確定模型計算區域；構建xy坐標系，確定每個案件發生的地點坐標(x，y)；

b、曼哈頓距離的計算

將地模型計算區域劃分為有限的柵格，并確定模型計算區域內每個小柵格點與所有犯罪點或案件相關點間的曼哈頓距離；

c、構建距離遞減函數f(d)

構建模型計算區域上的每一點對于每個犯罪地點的距離遞減函數f(d)；

d、相關性因子的模糊化

將高相關性的因子通過模糊化提取出來作為模型修正參數加入到cgt的計算模型中從而得到改進cgt模型；

e、計算犯罪分子居住地概率

通過將模型計算區域每一點的所有距離遞減函數值加權后相加，作為該點為犯罪分子居住地可能性的最后值。

優選地，所述的有效案件是指犯罪手法相似，作案對象相似，案件類型相似或作案地點相似，警察能夠判斷出屬于連環案件的案件。

優選地，步驟c中的距離遞減函數為：

當d<b時有：

當d≥b時有：

其中，φ是權重因數；b是緩沖區半徑(現有有效案件的距離統計數據的正態分布構建中的期望值，即現有有效案件曼哈頓距離d的平均值)；h、g是經驗指數。

優選地，步驟d高相關性的因子包括交通環境g、警務安保p和犯罪地點概率因子u，交通環境由道路條數來確定，設某一小網格區域內道路條數在0～10之間；小網格區域內的警務安保由警察和其他安保人員人數確定，設某一小網格區域內警察和其他安保人員人數在0～10之間；

選用三角形隸屬函數實現交通環境的模糊化，具體公式如下所示：

上式中x是小網格區域內的道路條數；

選用三角形隸屬函數實現警務安保的模糊化，具體公式如下所示：

上式中x是小網格區域內的警務安保人員的個數；

作案交通環境分為三個模糊集，作案交通環境g、警務安保p及犯罪地點概率因子u的模糊語言變量子集分別如下：

g：{sg(交通環境不便),mg(交通環境適中),lg(交通環境便利)}

p：{sp(警務安保差),mp(警務安保適中),lp(警務安保好)}

u：{vb(可能性很大),b(可能性大),m(可能性適中),s(可能性小),vs(可能性很小)}根據以上兩個隸數函數，得到以下模糊規。

優選地，犯罪地點概率因子選用三角形隸屬函數實現概率因子的模糊化，具體公式如下所示：

將所有格網點(i,j)通過模糊化后，可以得到格網點模糊系數hij＝uij。

優選地，通過模糊控制后，得到改進后的地理目標模型，如下所示：

式中，p'ij是嫌疑人居住在網格點(i,j)的概率值，k是一個常數，用來放大整體的概率數值；hij是格網點模糊系數；f和g均為經驗值常數；xi、yj分別是第i行，第j列對應格網點的坐標值；xn、yn是第n個案件點的坐標值。

3.有益效果

采用本發明提供的技術方案，與現有技術相比，具有如下有益效果：

(1)本發明的一種系列犯罪案件地理目標預測方法，通過研究交通環境因素、警察因素、人口因素、被害人職業因素等因素與嫌疑人落腳點的相關性，發現地理警察因素、環境因素與嫌疑人落腳點具有較高的相關性，提高了犯罪地點預測的準確率；

(2)本發明的一種系列犯罪案件地理目標預測方法，將高相關性的因素通過模糊化提取出來作為模型修正參數加入到cgt的計算模型中，從而得到改進cgt模型，并取得了比較好的預測效果，預測命中百分率至少高于原始cgt模型6％以上；

(3)本發明的一種系列犯罪案件地理目標預測方法，通過確定模型計算區域不僅可以估測犯罪分子的活動范圍使偵查范圍大大減小，還能提高偵查人員預測犯罪嫌疑人居住的精度。

附圖說明

圖1為地理畫像犯罪區域圖；

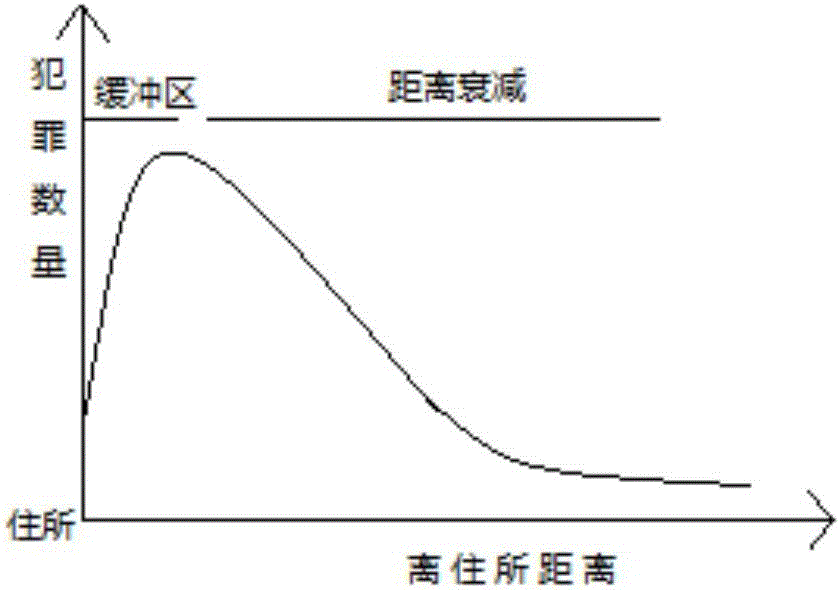
圖2為距離衰減模式曲線；

圖3為本發明的搜索區域面積效用曲線；

圖4為本發明的命中百分率效用曲線。

具體實施方式

為進一步了解本發明的內容，結合附圖及實施例對本發明作詳細描述。

對比例1

目前，國內外對犯罪分子最有可能的下次作案地點和居住地點預測主要有兩種方法。一種是以形態學為基礎的地理畫像預測方法，主要是“圓圈假設”理論，如圖1所示。地理畫像犯罪區域圖中幾乎包含了系列案件發生的地點以及與案件相關地點。另一種是鄰近度方法，即犯罪嫌疑人活動距離，通過模擬距離衰減曲線預測犯罪嫌疑人位置。大多數地理畫像的研究和預測是以距離衰減曲線為基礎的。世界上出現最早并且已經應用最成熟的是rossmo的犯罪地理目標模型。該模型采用一個分段函數對犯罪嫌疑人活動距離的距離衰減曲線如圖2所示進行模擬，將嫌疑人鎖定在一個很小的區域范圍內，從而大大減小了警務人員對犯罪嫌疑人搜尋排查的時間。通過在地圖上進行描點定位，將犯罪嫌疑人作案地點進行標記并且排除異常點，求一點d(x0,y0)使得它到各個有效案發地點距離之和的平均值最小從而求出最小半徑，公式如下：

其中，i＝1,2,3,……,n。

假設，a＝sxx(x0，y0)；b＝sxy(x0，y0)；c＝syy(x0，y0)。

因為故函數s有極小值。

令且求出極小值點(x^*,y^*)并計算出半徑r的值，

其中，(x0,y0)為犯罪分子可能居住或逗留地點坐標，(xi，yi)為排除異常點之后的案發地點坐標。

以這個極小值點為圓心，r為半徑作出案發區域的圓環，從而運用地理畫像方法從宏觀上對犯罪分子下一次作案地點進行刻畫。

對比例2

基于cgt模型的犯罪嫌疑人居住地預測方法具體如下：

(1)模型計算區域的確定

依據犯罪分子有效案件(有效案件是指犯罪手法相似，作案對象相似，案件類型相似或作案地點相似等，警察能夠判斷出屬于連環案件的)點的分布確定模型計算區域(地圖)。計算區域范圍的確定對犯罪嫌疑人居住地的預測具有重要意義。通過確定模型計算區域不僅可以估測犯罪分子的活動范圍使偵查范圍大大減小，還能提高偵查人員預測犯罪嫌疑人居住的精度。犯罪嫌疑人有效案件點可能是罪犯與被害人相遇的地點、作案實施地點(搶劫地點、偷竊地點、殺人現場、拋尸地點等)、犯罪嫌疑人臨時逗留地點等。從有效案件點中獲取x最大值xmax，x最小值xmin，y最大值ymax，y最小值ymin分別為：

xhigh、xmin、yhigh、ymin分別代表地圖計算區域的最東部的x值、最西部的x值、最北部的y值、最南部的y值，m是犯罪地點的總數。

(2)曼哈頓距離的計算

將地圖上的計算區域劃分為有限的柵格，構建xy坐標系，確定網格原點對應為xy軸的原點，優選模型計算區域的中心作為原點，便于計算，處理速度快，節省運算處理時間，并確定模型計算區域中每個小柵格的中心點與所有犯罪點或案件相關點間的曼哈頓距離d。地圖上任意一小柵格的中心點(xi，yj)與任意第n個犯罪點(xn，yn，n代表案件的編號)的曼哈頓距離d為：

d＝|xi-xn|+|yi-yn|

(3)構建距離遞減函數f(d)

設計距離遞減函數f(d)，其中曼哈頓距離d為獨立變量。模型計算區域上的每一點對于每個犯罪地點或者犯罪相關地點都有一個這樣的函數值，如果存在m個犯罪地點或者犯罪相關地點，則模型計算區域上每一點均有對應的m個數值(對應m個d，m個f(d))。

當d<b時有：

當d≥b時有：

其中，φ是權重因數；b是緩沖區半徑(現有有效案件的距離統計數據的正態分布構建中的期望值，即現有有效案件曼哈頓距離d的平均值)；h、g是經驗指數。

(4)通過將模型計算區域中每一點(任意一小柵格的中心點)的所有距離遞減函數值加權后相加，作為該點為犯罪分子居住地可能性的最后值。，某一點的值越大表明該點包含犯罪分子居住地或逗留地的可能性越大。其中概率值最高點即為嫌疑人最可能的落腳地點具體函數如下：

其中，pij表示了小柵格中心點(xi，yj)是犯罪歸屬點的可能性；k是經驗常數。某一個網格區域內，計算得到的概率pij最大，就是預測到的下一次犯罪發生(嫌疑人最可能的落腳地點)的地點。

實施例1

地理畫像領域取得了一些研究與應用成果，但是也存在著少許不足：cgt模型僅基于案件點時空信息進行預測，忽略了交通環境、警務監督等對嫌疑人選擇落腳點的影響，缺乏對嫌疑人落腳點選擇機理研究，導致模型在預測中存在預測精度不理想、或預測失敗的問題。

通過研究交通環境因子與嫌疑人落腳點的相關性，發現交通環境因素、警察因素與嫌疑人落腳點具有較高的相關性。因此，本專利將高相關性的因子通過模糊化提取出來作為模型修正參數加入到cgt的計算模型中從而得到改進cgt模型，以期獲得更好的預測效果，具體如下。

交通環境可以由道路條數來確定，可設某一局部地區(小網格區域內)道路條數在0～10之間；警務安保可由警察和其他安保人員人數確定(小網格區域內)，可設某一局部地區(小網格區域內)警察和其他安保人員人數在0～10之間；

選用三角形隸屬函數實現交通環境的模糊化，具體公式如下所示：

上式中x是小網格區域內的道路條數；

選用三角形隸屬函數實現警務安保的模糊化，具體公式如下所示：

上式中x是小網格區域內的警務安保人員的個數；

作案交通環境分為三個模糊集，作案交通環境g、警務安保p及犯罪地點概率因子u的模糊語言變量子集分別如下：

g：{sg(交通環境不便),mg(交通環境適中),lg(交通環境便利)}

p：{sp(警務安保差),mp(警務安保適中),lp(警務安保好)}

u：{vb(可能性很大),b(可能性大),m(可能性適中),s(可能性小),vs(可能性很小)}

根據以上兩個隸數函數，得到以下模糊規則表：

表1模糊規則表

犯罪地點概率因子，是指嫌疑人最可能的落腳地點的概率因子。

犯罪地點概率因子，選用三角形隸屬函數實現概率因子的模糊化，具體公式如下所示：

將所有格網點(i,j)通過模糊化后，可以得到格網點模糊系數hij＝uij(可變的概率因子)。

通過模糊控制后，由以上公式可以得到改進后的地理目標模型，如下所示：

式中，p'ij是嫌疑人居住在網格點(i,j)的概率值，k是一個常數，用來放大整體的概率數值；hij是格網點模糊系數；f和g均為經驗值常數；xi、yj分別是第i行，第j列對應格網點的坐標值；xn、yn是第n個案件點的坐標值。

實施例2

以某連環案件為例，從以往發生的有效案件中提取出那些作案手法相似，作案對象相似，案件類型相似或作案地點相似，警察能夠判斷出屬于連環案件的案件。為判定下一次犯罪發生地，對犯罪分子所在地區進行預估，在警用綜合平臺上應用本實施例的系列犯罪案件地理目標預測方法，從警用綜合平臺上調取出一個犯罪分子尚未歸案的連環案件，對以往的作案地點進行統計(此處，共計8個)，在這8各作案地點，劃定模型計算區域，并在警用平臺上調取出該區域內的警用安保和交通環境，本實施例中將交通環境簡化未道路數量，在該區域內構建xy坐標系，并以區域中心作為原點，將模型計算區域劃分成10個小格柵，計算每個格柵的曼哈頓距離，運用實施例1的計算方法，對每個格柵的犯罪發生概率進行預測，對比找出嫌疑人最可能的落腳地點對應的小格柵。

cgt模型與改進cgt模型預測范圍內嫌疑人的面積誤差效用曲線，圖3為搜索區域面積效用曲線，圖4為命中百分率效用曲線。

圖3中，可以看出改進的cgt模型比原始cgt模型預測效果要好。改進后模型曲線在原始模型曲線之上，以6km²時的搜索區域為例，原始cgt模型中有73％左右的樣本在6km²搜索區域內，而改進的cgt模型有88％左右的樣本在6km²搜索區域內，從而說明改進后的模型比原始模型效果好。

圖4中，可以看出改進的cgt模型比原始cgt模型預測效果要好。改進后模型曲線在原始模型曲線之下，以50％的命中百分率為例，原始cgt模型中命中百分率低于50％的樣本有72％左右，而改進的cgt模型中命中百分率低于50％的樣本有60％左右，從而說明改進后的模型比原始模型效果好。

將交通環境因素、警務監督因素通過模糊化提取出來作為模型修正參數加入到cgt的計算模型中從而得到改進cgt模型。通過實例應用表明，改進cgt模型比原始cgt模型取得了較好的預測效果，命中百分率至少高于原始cgt模型6％以上，對公安機關提高破案效率具有重要意義。

以上示意性的對本發明及其實施方式進行了描述，該描述沒有限制性，附圖中所示的也只是本發明的實施方式之一，實際的結構并不局限于此。所以，如果本領域的普通技術人員受其啟示，在不脫離本發明創造宗旨的情況下，不經創造性的設計出與該技術方案相似的結構方式及實施例，均應屬于本發明的保護范圍。