本發明涉及應用磨損比耗指數預測滾刀磨損量的分層求和法，屬于地下隧道工程的施工技術領域。

背景技術：

盾構掘進高強度復合地層，工程面臨的最大風險是掘進速率緩慢或掘進困難，且刀具磨損嚴重。刀具磨損已經成為一個影響工程進度及成本的關鍵問題。刀具的完善性及刀具的磨損狀態判斷是盾構掘進中的關鍵因素，如何準確地定量預測滾刀的磨損量并判斷磨損狀態，對盾構高效掘進至關重要。準確預測盤形滾刀磨損量，對提高盾構施工效益有重要意義。目前國內外滾刀磨損預測方法可歸為兩大技術路徑：力學分析法及經驗預測法。力學模型中的關鍵系數受試驗條件及巖體性質影響顯著，在復合地層滾刀磨損預測應用中存在局限。經驗預測法，對地層分布在滾刀軌跡、掘進方向上的區分不足，影響其在巖層分布多變的復合地層中的適用性。

技術實現要素：

本發明針對現有技術的不足，提出了應用磨損比耗指數預測滾刀磨損量的分層求和法。

本發明是應用磨損比耗指數預測滾刀磨損量的分層求和法，它包括以下步驟：

步驟一：統計由盾構機自動記錄的盾構掘進每環的掘進參數平均值；

步驟二：進行滾刀刀圈的磨損量量測，分別記錄在每次開倉檢查或換刀時的各滾刀磨損增加量δ^ωi-l-j，滾刀破巖地層為復合地層時記為δ^δi-l-j；

步驟三：計算并記錄下掘進過程中不同滾刀掘進每一環中各地層的破巖體積；

步驟四：計算磨損比耗指數swi(specificwearindex)；

步驟五：將位置各異的滾刀的磨損增加量δ^ωi-l-j按掘進地層重新分類統計，作為回歸分析樣本，將同種地層中的swi所對應的掘進參數集合、swi所對應的掘進參數的若干次冪作為元素集，進行元素集間笛卡爾乘積運算，得到屬于同種地層swi的單項變量及二元復合變量集合，作為多元回歸分析的自變量集；

步驟六：對滾刀掘進各種均質地層的swi樣本及相應自變量集元素進行多元逐步線性回歸運算，得到分別獨立屬于各種均質地層的swi與掘進參數間的高階多項式函數關系，按照共性提升原則，將屬于不同均質地層的swi與掘進參數間的高階多項式函數關系中相同的自變量抽出來，將它們線性組合，作為預測均質地層滾刀swi的通式，即swi預測方程；

步驟七：計算屬于不同地層的swi預測方程諸系數的離均差率mdra、mdrb、mdrc、mdrk；

步驟八：根據勘察報告，了解掘進地層的分布情況；如果掘進地層是復合地層，也就是說掌子面由若干個地層組合而成，就根據地層參數，從而確定了掌子面里面每一個地層的bq值或[bq]值；

步驟九：確定屬于掌子面里面各地層swi方程系數；即根據勘察報告計算得出地層bq值或[bq]值，在橫坐標上找到該地層bq值或[bq]值，對應的點并過該點作一條垂線，垂線分別和mdra與bq值或[bq]值的關系曲線、mdrb與bq值或[bq]值的關系曲線、mdrc與bq值或[bq]值的關系曲線、mdrk與bq值或[bq]值的關系曲線的4個交點的縱坐標，就是屬于該地層的swi預測方程諸系數的離均差率mdra、mdrb、mdrc、mdrk，并在此基礎上確定屬于掌子面里面某一個地層swi方程系數a、b、c、k的具體值；

步驟十：提出一組掘進速率v和刀盤轉速n的試算值，代入到a、b、c、k為具體數值的swi預測方程中，就得到了屬于這一地層的、這一組v和n對應的磨損比耗指數預測值swi^ω*；

步驟十一：提出與掘進速率v的試算值和刀盤轉速n的試算值相對應的開倉環號預選值，再從勘察報告和地層剖面圖中計算出每一環里各地層的體積把它們和與地層對應的swi預測值相乘，就得到了任意一環中各地層對應的磨損增量，如下式：

步驟十二：

把一環中各地層對應的磨損增量求和，就得到了滾刀在任意一環的磨損增量w為一環中地層種類數量，如下式：

步驟十三：計算兩次開倉之間掘進了q環(從第p+1環到第p+q環)的磨損增量，如下式：

步驟十四：滾刀壽命內，即從換上新刀到更換下來，中間開了t次倉，根據下式計算滾刀壽命內的磨損量，用△表示，和磨損增量δ相區別：

步驟十五：盾構機在一定刀盤扭矩和掘進速率之下掘進時，可以根據刀盤扭矩和掘進速率實時預測滾刀達到預警值所要掘進的長度或環數；當選定開倉位置時，即在確定的掘進長度條件下，通過計算掘進速率試算值和刀盤扭矩試算值所對應的滾刀壽命內的刀盤磨損量將滾刀壽命內的磨損量與預警值(如：20mm±1mm)做比較，如果預測的磨損量低于20mm，則滾刀利用效率太低；如果磨損量預測值大于20mm，則滾刀與圍巖間作用過于劇烈；這些情況需要重新選取v和n，直到得到滿足要求的v和n，并將滿足要求的v和n設定為施工參考值。

原理和優勢：

針對復合地層在滾刀軌跡及掘進方向上的地層分布變化，通過逐刀統計軌跡各異的滾刀的“磨損比耗指數”，作為磨損量回歸分析目標值。最大的好處是消除了滾刀安裝半徑對滾刀間磨損增加量差異的影響，將各滾刀的“磨損比耗指數”按滾刀掘進地層分類統計及回歸分析，得到分別屬于各種均質地層的磨損比耗指數經驗公式。提出適用于復合地層的應用磨損比耗指數預測滾刀磨損量的分層求和法，在考慮滾刀軌跡差異對滾刀磨損量影響的同時提高了經驗預測法的地層適用性。

首次提出基于磨損比耗指數回歸分析與滾刀破巖體積分層統計的應用磨損比耗指數預測滾刀磨損量的分層求和法，實現了對刀盤上任意位置的正面滾刀及中心滾刀的磨損量及壽命的定量預測，有效地解決了復雜地層滾刀磨損量及壽命的定量預測的難題。應用磨損比耗指數預測滾刀磨損量的分層求和法對滾刀磨損量與壽命具有良好的預測精度，豐富了滾刀磨損預測研究成果，有利于科學編制預算、合理安排施工進度、提高盾構掘進效率，具有重要的理論意義與實用價值。

附圖說明

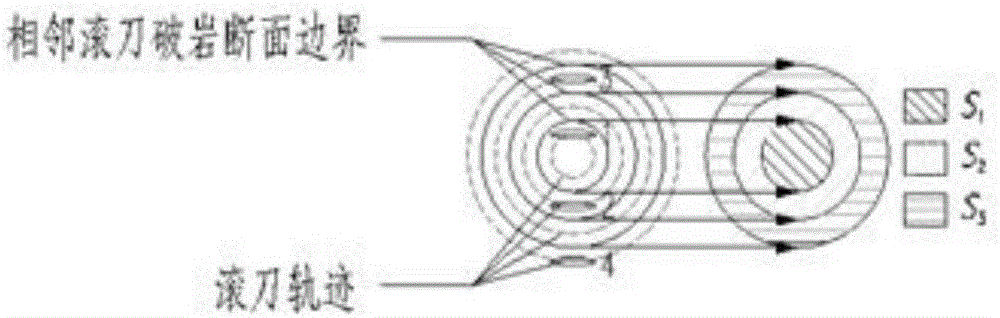
圖1滾刀破巖區域劃分截面示意圖；

圖2滾刀破巖空間立體示意圖；

圖3滾刀swi及破巖體積分層統計示意圖；

圖4j31-2地層swi實測值與回歸曲面圖；

圖5j31-3r地層swi實測值與回歸曲面圖；

圖6j31-3p地層swi實測值與回歸曲面圖；

圖7j31-3地層swi實測值與回歸曲面圖；

圖8不同地層swi預測方程諸系數的離均差率與地層bq值或[bq]值的關系示意圖；

圖9確定屬于掌子面里面某一個地層的swi方程系數a、b、c、k的具體值的方法；

圖10應用磨損比耗指數預測滾刀磨損量的分層求和法流程圖；

具體實施方法

本發明應用磨損比耗指數預測滾刀磨損量的分層求和法，包括以下步驟：

步驟一：

統計由盾構機自動記錄的盾構掘進每環的掘進參數平均值(vi-l-j-m,ni-l-j-m,fi-l-j-m,ti-l-j-m,pi-l-j-m)，其中，v為推進速率、n為刀盤轉速、f為有效推力、t為扭矩、p為土倉壓力，i為滾刀編號，l為滾刀更換次序，j為滾刀壽命內的開倉量測次序，m為環號；

步驟二：

進行滾刀刀圈的磨損量量測，分別記錄在每次開倉檢查或換刀時的各滾刀磨損增加量δ^ωi-l-j，滾刀破巖地層為復合地層時記為δ^δi-l-j，ω為滾刀破巖地層序號；

步驟三：

計算并記錄下掘進過程中不同滾刀掘進每一環的破巖體積；

以圖1至圖3為例具體說明。

如圖1所示，圖中標號1、2、3、4，分別代表四把不同的滾刀，在各自的軌跡上進行掘進。統計時：取相鄰滾刀外緣間距中點為相鄰滾刀破巖斷面邊界。

如圖2中，ω1、ω2、ω3分別為滾刀掘進三種不同地層。

如圖3中，ω1、ω2、ω3、ω4分別為滾刀掘進四種不同地層。

以滾刀為研究對象，滾刀在環形軌跡上掘進時，可能遇到不同的地層，滾刀在地層中掘進的空心柱體空間的體積是空心柱體中各地層體積之和。如圖3表格中所示，將滾刀在地層中掘進的空心柱體空間中的各地層體積分層統計。其中，如果某次開倉量測滾刀磨損量與上一次開倉量測滾刀磨損量之間，滾刀掘進破巖空心柱體空間中的地層種類多于一種，即滾刀掘進的是復合地層，由于滾刀磨損增加量δ^△i-l-j與該階段滾刀在復合地層中的破巖體積之和相對應，無法確定滾刀磨損增加量δ^△i-l-j與該階段滾刀在復合地層中各地層相應的破巖體積之間的對應關系，無法計算得到swi實測值；如果某次開倉量測滾刀磨損量與上一次開倉量測滾刀磨損量之間，滾刀掘進的是均質地層，這時滾刀磨損增加量δ^ωi-l-j與該階段滾刀掘進地層的類型和體積均明確對應，可以計算得到swi實測值。

具體來說，如式(1)，以單把滾刀為研究對象，取軌跡相鄰的滾刀外緣間距中點為相鄰滾刀破巖斷面邊界，滾刀在環形軌跡上掘進一環，滾刀破巖產生的空心柱體空間的體積，即滾刀掘進每環的空心柱體的總體積vi-l-j-m為：

vi-l-j-m＝l×si-l-j-m(1)

按所遇到的不同的地層，計算并統計各滾刀掘進每環產生的空心柱體中各地層體積，記為v^ωi-l-j-m，且vi-l-j-m＝σv^ωi-l-j-m；其中：l為盾構管片環寬，si-l-j-m為該滾刀破巖環形區域的面積；

步驟四：

進行滾刀的swi統計。各滾刀與刀盤旋轉中心之間的距離(滾刀安裝半徑)均不相同，導致掘進相同里程時各滾刀破巖體積不同。定義磨損比耗指數(specificwearindex，swi)，即單位破巖體積對應的滾刀磨損增加量，如式(2)。

swi的意義在于：磨損增加量和半徑正相關，破巖體積和半徑正相關，兩者相除，得到swi，實現了對半徑的降次處理。所以，swi受半徑的影響大大小于磨損增加量，可以認為“消除了滾刀安裝半徑對滾刀間磨損增加量差異的影響”。

滾刀是螺線前進的，但掘進速率變化太大，無法準確計算出某一段里滾刀運動的螺線長度。所以，我們把破巖體積這個確定的量作為分母，方便分析與應用。

步驟五：

最后，將位置各異的滾刀的磨損增加量按掘進地層重新分類統計，作為回歸分析樣本。將同種地層swi相應的掘進參數集合及掘進參數若干次冪作為元素集，進行元素集間笛卡爾乘積運算，得到屬于同種地層swi的單項變量及二元復合變量集合，作為多元回歸分析的自變量集。

步驟六：

對滾刀掘進各種均質地層的swi樣本及相應自變量集元素進行多元逐步線性回歸運算，得到分別獨立屬于各種均質地層的swi與掘進參數間的高階多項式函數關系。按照共性提升原則，將屬于各種均質地層的swi與掘進參數間的高階多項式函數關系中相同的自變量抽出來，將它們線性組合成式(3)，作為預測均質地層滾刀磨損速率的通式。

swi^ω*＝kv^an^b+c(3)

式中，v為掘進速率；n為刀盤轉速；a、b、c及k均為回歸方程系數，swi^ω*為swi^ω的預測值。該通式應用于南京市寧高城際軌跡交通二期工程盾構隧道項目，如圖4～7為不同地層swi預測方程計算結果，其中v/mm·min^-1表示掘進速率v的單位為mm·min^-1；n/r·min^-1表示刀盤轉速n的單位為r·min^-1。

如表1及表2，通過對比預測值和實測值，得到回歸方程系數及方差分析結果：因為自變量顯著性在各地層中均小于0.05且相關系數較大，所以式(3)具有統計意義，對于滾刀磨損比耗指數具有較好的預測效果。

表1均質地層swi回歸計算系數

表2預測均質地層滾刀磨損速率的通式的預測實例

步驟七：

如圖8，利用式(4)、式(5)、式(6)和式(7)，計算屬于不同地層swi預測方程諸系數的離均差率(mdra、mdrb、mdrc、mdrk)。

步驟八：

根據工程勘察報告，可以了解到掘進地層的分布情況。如果掘進地層是復合地層，也就是說掌子面由若干個地層組合而成，我們就根據地層參數如巖體完整性指數和巖石飽和單軸抗壓強度，從而確定了掌子面里面每一個地層的bq值(或[bq]值)。

步驟九：

確定屬于掌子面里面各地層swi方程系數。如圖9，根據勘察報告計算得出地層bq值(或[bq]值)，在橫坐標上找到該地層bq值(或[bq]值)對應的點并過該點作一條垂線，垂線分別和mdra與bq值(或[bq]值)的關系曲線、mdrb與bq值(或[bq]值)的關系曲線、mdrc與bq值(或[bq]值)的關系曲線、mdrk與bq值(或[bq]值)的關系曲線的4個交點的縱坐標，就是屬于該地層的swi預測方程諸系數的離均差率(mdra、mdrb、mdrc、mdrk)。根據式(4)、式(5)、式(6)和式(7)，確定屬于掌子面里面某一個地層swi方程系數a、b、c、k的具體值。

對掌子面內各地層均進行步驟九內的運算，得到屬于掌子面里面各地層swi方程系數。

步驟十：

如圖10，提出一組掘進速率v和刀盤轉速n的試算值，代入到a、b、c、k為具體數值的swi預測方程中，就得到了屬于這一地層的、這一組v和n對應的磨損比耗指數預測值swi^ω*。

步驟十一：

當步驟一所述的掘進參數改變時，滾刀和圍巖間的相互作用發生改變，滾刀的磨損狀態隨之變化，即在滾刀換刀磨損量一定的前提下，掘進環數隨掘進參數的變化而變化。然而，更換刀具時掘進停止，在圍巖條件較差的地段可能存在塌方等隱患，換刀時盾構機所處的環號不能隨意設置；為了盡可能提高滾刀利用效率，應該在滾刀換刀前盡可能掘進更長的距離，且掘進速率要滿足工期要求。所以，可以通過預測并控制掘進參數，實現滾刀掘進環數的定量預測和控制。

如圖10，提出與掘進速率v的試算值和刀盤轉速n的試算值相對應的開倉環號預選值，再從勘察報告和地層剖面圖中計算出每一環里各地層的體積把它們和與地層對應的swi預測值相乘，就得到了任意一環中各地層對應的磨損增量，如式(8)

步驟十二：

如式(9)，把一環中各地層對應的磨損增量求和，就得到了滾刀在任意一環的磨損增量w為一環中地層種類數量。

步驟十三：

如圖4，兩次開倉之間掘進了q環(從第p+1環到第p+q環)的磨損增量根據式(10)計算。

具體來說，公式(10)表示：當p環時開倉，測量磨損量一次；當從第p+1環開始掘進到第p+q環時，再開倉測量磨損量一次；兩次開倉間的磨損增量，是與第p+1環到第p+q環之間滾刀的破巖量相對應的；

步驟十四：

如圖10，若在滾刀壽命內，即從換上新刀到更換下來，中間開了t次倉，那這就是滾刀壽命內的磨損量，用大寫的△表示，和磨損增量小寫的δ相區別。

步驟十五：

盾構掘進施工中，掘進參數的選取和開倉環號的安排不是隨意性的。掘進速率過大或刀盤扭矩過大，表明滾刀與圍巖之間作用劇烈，有損壞滾刀、刀座、刀盤、刀盤驅動設備的隱患。在圍巖完整程度較低、地下水豐富的地層，盾構停工開倉會導致地層異常沉降和掌子面坍塌，嚴重威脅盾構機和操作人員的安全。所以，需要根據勘察報告，選定地層完整程度較高、地下水較少的區間安排開倉換刀作業。為了實現盾構機掘進至預定開倉位置之前的磨損量不超過滾刀磨損量預警值，需要根據擬定的掘進距離來選擇合適的掘進參數。當盾構機在一定刀盤扭矩和掘進速率之下開展掘進時，可以根據刀盤扭矩和掘進速率實時預測滾刀達到預警值所要掘進的長度或環數。

具體應用方法如下：

如圖10，滾刀壽命內的磨損量達到預警值，應該更換滾刀。如果預測的滾刀壽命內的磨損量低于20mm±1mm，則滾刀利用效率太低；如果磨損量預測值大于20mm±1mm，則滾刀與圍巖間作用過于劇烈。

當選定開倉位置時，即在某確定的掘進長度條件下，通過計算掘進速率試算值和刀盤扭矩試算值所對應的刀盤磨損量將滾刀壽命內的磨損量與預警值20mm做比較，如果預測的磨損量低于20mm，則滾刀利用效率太低；如果磨損量預測值大于20mm，則滾刀與圍巖間作用過于劇烈。這些情況需要重新選取v和n，直到得到滿足要求的v和n，并將滿足要求的v和n設定為施工參考值。

當實際掘進時需要判定一定掘進速率和刀盤扭矩條件下的滾刀磨損狀態時，應根據掘進速率和刀盤扭矩實測值，結合地層分布及地層參數，可以預測一定掘進速率和刀盤扭矩條件下滾刀掘進任意距離時的磨損量。當接近20mm時，應提前安排開倉換刀準備工作，防止滾刀損壞后更換不及時導致的刀座或刀盤損壞，提高掘進效率。

本專利方法已應用于南京市寧高城際軌跡交通二期工程盾構隧道項目，如表3，相對于實測值，8具中心滾刀及24具正面滾刀的磨損量預測值平均相對偏差多在20％～30％內，而滾刀壽命預測值平均相對偏差均低于20％且多在7％～16％內，表明swi回歸分析與復合地層滾刀磨損量分層求和法對磨損量及滾刀壽命均具有較高的預測精度，且其對滾刀壽命的預測更為準確。

表3滾刀磨損量及壽命預測值相對偏差

表3中，dcw為磨損量預測值與實測值間相對偏差，根據式(12)計算；dcl為20mm滾刀更換磨損水平的滾刀壽命預測值與實測值，間相對偏差根據式(13)計算。