本發明屬于機械制造技術領域，涉及到五軸數控機床銑削切削過程中顫振穩定域建模方法，尤其是球頭銑刀在五軸數控機床銑削切削過程中顫振穩定域葉瓣圖建模方法。

背景技術：

機械制造業作為國家經濟增長支柱，已經發展了上百年，建立了比較系統的理論體系，積累了豐富的實踐經驗，但隨著科學技術水平的提高，迫切的需要其向高速、高效和高精度方向發展。

高速銑削加工是先進制造技術中最重要的基礎技術之一，是目前最重要、應用最普遍的加工方式，然而在高速銑削過程中不合適的切削參數導致的切削顫振嚴重地影響到了加工效率、精度、質量以及穩定性，是制約高速銑削技術快速發展的關鍵因素。

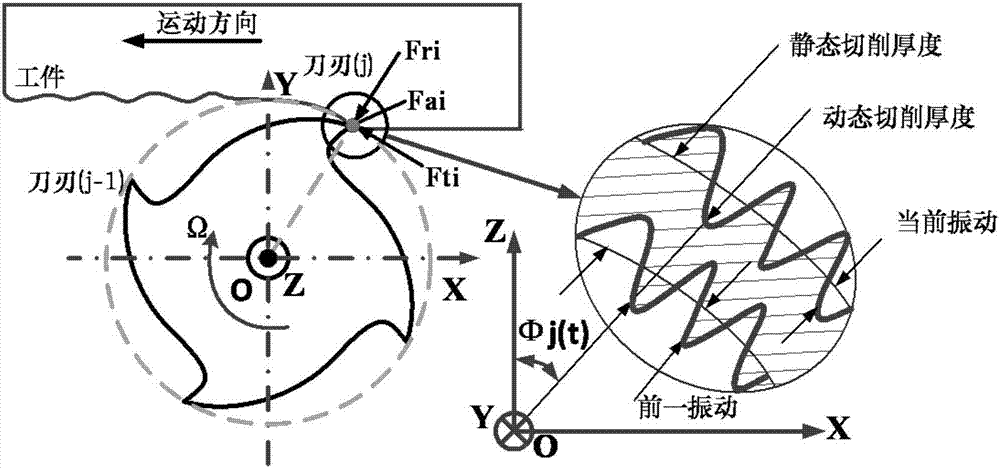
國內外學者對切削顫振進行了大量探索，研究了多種顫振形成的機理，其中再生型顫振是人們認為產生切削過程中產生顫振最直接、最根本的原因。如圖1所示，再生型顫振理論指出，由于機床結構振動，當刀具進行切削時，工件的已加工表面會留下表面振紋，當刀具再一次切削到這些遺留有振紋的工件表面時，瞬時切削厚度由名義切削厚度和動態切削厚度疊加組成，這種切削厚度的變化引起切削力的波動，反過來又引起切削刀具和工件之間的相對振動，使刀具和工件在切削過程中產生振動位移，從而再次在工件已加工表面留下振紋，根據前后兩次振紋之間的相位差，在靠近但不等于加工系統主結構模態的顫振頻率處，隨著加工系統的切削厚度不斷增長，造成切削力和振動位移的不斷上升現象，形成強烈的自激振動，這種自激振動就是再生顫振，圖2為再生顫振機理模型。

避免切削顫振最有效辦法是在加工前構建銑削顫振穩定域葉瓣圖，即在給定切削條件下，繪制出軸向臨界切削深度隨主軸轉速變化的函數關系。葉瓣圖的構建能夠為加工前切削參數的選擇提供指導，可以有效防止加工中顫振的發生。而球頭銑刀是典型的點接觸加工，具有很好的法矢自適應性，是高速銑削加工中應用最廣的刀具之一，因此構造出針對球頭銑刀加工過程中的穩定性葉瓣圖意義重大。

目前，國內外還沒有針對球頭銑刀在五軸數控機床加工過程中的顫振穩定域葉瓣圖建模方法。有部分學者對三軸數控機床上球頭銑刀顫振穩定域葉瓣圖建模方法進行了研究，其中具有代表性的有：李忠群等人提出的基于龍格庫塔的時域求解法；dingh等人提出的全離散時域求解法；limingzhen等人提出的完全離散時域數值求解法。但是不論是龍格庫塔法，全離散法，還是改進的完全離散法本質上都屬于差分類方法，它們的優點是易于實現，但差分引起的誤差很難從根本上消除。同時，五軸數控機床和三軸數控機床的加工方式不同，刀具姿態不同，故球頭銑刀在三軸數控機床的建模方法并不能適用于其在五軸數控機床上；因此如何在更先進的五軸數控機床上對球頭銑刀進行高精度的顫振穩定域葉瓣圖構建將是一個亟待解決的問題。

技術實現要素：

為了解決現有技術存在的問題，本發明提供一種五軸數控機床加工中基于精細積分的球頭銑刀顫振穩定域葉瓣圖建模方法。

本發明的技術方案為：

一種五軸數控機床加工中基于精細積分的球頭銑刀顫振穩定域葉瓣圖建模方法，包括以下步驟：

步驟一，建立球頭銑刀刀具-工件動力學方程；

步驟二，求解球頭銑刀刀齒上的動態切削力ftx(t)和fty(t)；

步驟三，五軸數控機床平面加工中球頭銑刀與工件的接觸區域半解析建模；

步驟四，精細積分法對刀具-工件動力學方程時域數值求解；

步驟五，葉瓣圖構建。

本發明的有益效果為：運用精細積分法對銑削系統二階動力學方程進行高精度時域數值求解，克服了傳統數值求解法不能同時兼顧計算精度、計算效率和穩定性的弊端；精準識別出球頭銑刀存在前傾角和側傾角時與工件接觸區域邊界的投影方程，在單齒切削周期內球頭銑刀視為圓弧切削的基礎上，通過球頭銑刀與工件的接觸區域投影邊界方程和切削刃不同時刻的投影方程的關系，確定出時域數值方程中所需要的瞬時參與切削的刀刃數目和參與切削刀刃的實際切削部位，利用floquet定理獲得了不同轉速下臨界切削深度，構建出了球頭銑刀存在前傾角和側傾角時的顫振穩定域葉瓣圖。

附圖說明

圖1是球頭銑刀銑削過程中再生顫振發生機理示意圖。

圖2是球頭銑刀銑削過程中再生顫振機理模型。

圖3是球頭銑刀銑削動力學模型。

圖4是球頭銑刀螺旋切削刃幾何模型。

圖5是球頭銑刀-工件接觸區域示意圖。

圖6是球頭銑刀-工件接觸區域邊界組成示意圖。

圖7是球頭銑刀三維坐標x0-y0-z0建立示意圖。

圖8是推導出刀具前傾角為α，側傾角為零時的刀位點和刀觸點示意圖。

圖9是球頭銑刀三維坐標x1-y1-z1和x-y-z建立過程示意圖。

圖10是球頭銑刀三維坐標xp-yp-zp建立過程示意圖。

圖11是球頭銑刀三維坐標xf-yf-zf建立過程示意圖。

圖12是球頭銑刀三維坐標xm-ym-zm建立過程示意圖。

圖13是三維坐標xm-ym-zm示意圖。

圖14是b號投影線求解示意圖。

圖15是m點示意圖。

圖16是n點示意圖。

圖17是d號線投影求解中沿y1軸等間距取值示意圖。

圖18是d號線投影方程求解過程示意圖。

圖19是接觸區域在xm-ym坐標系投影示意圖。

圖20是第一條切削刃投影0-t5時刻位置。

圖21是tp＝0時刻，切削刃參與切削情況。

圖22是tp＜t1時刻，切削刃參與切削情況。

圖23是t1＜tp＜t2時刻，切削刃參與切削情況。

圖24是t2＜tp＜t3時刻，切削刃參與切削情況。

圖25是t3＜tp＜t4時刻，切削刃參與切削情況。

圖26是t4＜tp＜t5時刻，切削刃參與切削情況。

圖27是t5＜tp＜t6時刻，切削刃參與切削情況。

圖28是t6＜tp＜t7時刻，切削刃參與切削情況。

圖29是軸向切削深度小于l_jg時的接觸區域在xm-ym坐標系下投影的邊界組成。

圖30是葉瓣圖構建流程圖。

具體實施方式

以下結合技術方案和附圖詳細敘述本發明的具體實施方式。

五軸數控機床上加工中基于精細積分的球頭銑刀顫振穩定域葉瓣圖建模方法，包括以下步驟：

步驟一，建立球頭銑刀刀具-工件動力學方程

將球頭銑刀刀具-工件系統簡化為如圖3所示的二自由度系統，僅考慮進給方向x和法向y方向的刀具振動因素，建立如下所示的動力學方程：

其中，mtx，ξx，ωnx分別是為刀具系統x方向的模態質量，阻尼系數，固有頻率；mty，ξy，ωny分別是為刀具系統y方向的模態質量，阻尼系數，固有頻率；ftx(t)和fty(t)分別為在x，y方向上作用在銑刀上的動態切削力。

步驟二，求解球頭銑刀刀齒上的動態切削力ftx(t)和fty(t)

2.1建立球頭銑刀刀刃幾何模型

如圖4所示，建立球頭銑刀切削刃曲線幾何模型，由于每個切削微元與其所對應的軸向角存在一一映射關系，故切削微元坐標值可以表示為關于軸向角的函數，式(2)為第j刀刃上第i個切削微元坐標表達式。

其中，r為球頭銑刀半徑；μ切削刃螺旋角；t為切削過程中的時間(s)；k為第j刀刃上第i個切削微元的軸向接觸角，在一個切削刃上所能取值范圍為[0，π/2]；ψji(k)為第j刀刃上第i個切削微元徑向滯后角；φ10(t)為第一個切削刃端點處轉動的角度，n為刀具轉速(r/min)；φji(t)為第j刃上的第i個微元處瞬時徑向接觸角；nf為切削刃數目；xji(t)，yji(t)，zji(t)表示球頭銑刀第j刀刃上第i個切削微元在所建立的坐標系下的坐標值。

2.2球頭銑刀瞬時動態切削力計算

球頭銑刀第j刀刃上第i個切削微元(軸向角為k)所受的切向力dft,ji(φji(t),k)、徑向力dfr,ji(φji(t),k)、軸向力dfa,ji(φji(t),k)表示為：

其中，h(φji(t),kji)為第j刀刃上第i個切削微元瞬時切削厚度，ktc為切向力系數，krc為徑向力系數，kac為軸向力系數；db＝r·dk，r為球頭銑刀半徑。

2.3瞬時動態切削厚度計算

刀具瞬時銑削厚度由兩部分組成，一部分是瞬時靜態切削厚度，另一部分是瞬時動態切削厚度，瞬時靜態切削厚度與顫振無關，故將其忽略。

僅考慮刀具x和y方向的振動，球頭銑刀第j刀刃上第i個切削微元(軸向角為k)的瞬時動態銑削厚度為：

其中，x(t)-x(t-t)，y(t)-y(t-t)表示當前時刻t和前一個刀齒切削(t-t)時刻在x和y方向的動態振動矢量；t為時滯周期，在高速切削條件下，時滯周期等于單齒切削周期，即時滯周期nf為銑刀刀齒數；n為刀具轉速(r/min)。

2.4刀具瞬時動態切削力計算

通過坐標變換，獲得第j刀刃上第i個切削微元x，y方向動態切削力：

由式(3)，式(4)和式(5)得到如下結果：

其中，axx,ji(t)、axy,ji(t)、ayx,ji(t)、ayy,ji(t)如下所示。

確定每個切削刃在t時刻的參與切削片段的數目和每個參與切削的片段所對應的最大軸向角和最小軸向角，通過公式(6)就得到球頭銑刀上的動態切削力。

其中，

步驟三、五軸數控機床平面加工過程中球頭銑刀與工件接觸區域的半解析建模

球頭銑刀和工件的接觸區域是指在加工過程中刀具切入工件的區域。高速銑削條件下，在單齒切削周期內，球頭銑刀可視為圓弧切削，因此銑刀-工件接觸區域蘊含著式(6)中所需要的單齒切削周期內銑刀瞬時參與切削的刀刃數目和參與切削刀刃的實際切削部位等信息。

3.1進行刀具路徑規劃，設置加工參數

球頭銑刀在五軸數控機床上進行平面銑削，球頭銑刀球頭半徑為r，前傾角為α度，側傾角為β度，相鄰切削刀軌間距為l_xl，軸向切削深度為l_jg。

3.2確定前傾角為α度，側傾角為β度時球頭銑刀與工件接觸區域邊界組成，將接觸區域邊界方程的求解問題轉化為這些邊界在垂直于刀具軸線平面的投影方程的求解問題；

如圖5所示，前傾角為α，側傾角為β度時球頭銑刀與工件的接觸區域主要由圖6中所示的a，b，c，d四條線組成，其中，a號線為銑刀球頭與工件加工表面的交線，b號線為銑刀球頭與工件過渡表面的交線，c號線為本次走刀與上一次走刀在已加工表面留下的加工殘余而形成的線，d號線為銑刀球頭與上一次走刀留下的加工痕跡的交線。另外e號線為上一次走刀在工件加工表面留下的加工痕跡。

在切削靜力學和切削動力學模型中，確定刀刃某一時刻參加切削的上下邊界時都是在二維平面上進行的，因此根據球頭銑刀球頭部分沿垂直刀軸的方向具有單調分布的特點，將a，b，c，d四條線求解問題轉化為它們在垂直于刀具軸線平面的投影方程的求解問題。

3.3由刀具前傾角和側傾角為零度時的三維直角坐標系x0-y0-z0推導出刀具前傾角為α，側傾角為零度時的三維直角坐標系x-y-z

如圖7所示，建立刀具前傾角和側傾角都為零度時的三維直角坐標系x0-y0-z0，其中刀具頂點為原點o0，刀軸線為z0軸，x0軸與刀具進給方向相同。下面將由x0-y0-z0推導出刀具前傾角為α，側傾角為零度時的三維直角坐標系x-y-z，由于側傾角都為零度，故只需要在x0-z0平面討論即可。

如圖8所示，在x0-z0平面內，將z0軸以o0為原點，順時針傾斜α度(從y0負方向向原點看，α值為正數，順時針；α值為負數，逆時針，此處以α為正進行闡述)，傾斜之后的軸線就是刀具前傾角為α度，側傾角為零度時的刀具軸線，該直線方程z0＝tan(90-α)×x0與直線z0＝r的交點cir_0，即為刀具前傾角為α度，側傾角為零度時的球心，經計算cir_0的坐標為xcir_o＝r/tan(90-α)，zcir_0＝r。

以cir_0為原點，r為半徑建立圓的方程(x0-xcir_0)²+(z0-ycir_0)²＝r²，此圓方程與x0軸的切點即為前傾角為α度，側傾角為零度時的球頭銑刀的刀觸點dc_0，經計算dc_0的坐標xdc_0＝r/tan(90-α)，zdc_0＝0。

(x0-xcir_0)²+(z0-ycir_0)²＝r²方程與z0＝tan(90-α)×x0方程兩個交點中y0值較小的點即為前傾角為α度，側傾角為0度時的球頭銑刀的刀位點dw_0。經計算xdw_0＝r/tan(90-α)-r×sinα，zdw_0＝r-r×cosα。

如圖9所示，以dc_0為原點，建立三維直角坐標系x1-y1-z1，其中，x1-z1平面與x0-z0平面相重合，x1與x0相互重合且方向相同，y1與y0平行且方向相同。

如圖9所示，以dw_0為原點，方程z0＝tan(90-α)×x0為z軸建立三維直角坐標系x-y-z，其中x-z平面與x0-z0平面相重合，y與y0平行且方向相同，z軸正方向為遠離工件。x-y-z坐標系下，銑刀球頭輪廓方程x²+y²+(z-r)²＝r²。

3.4通過x-y-z三維坐標系，建立刀具前傾角為α，側傾角為β度時的xm-ym-zm坐標系，獲取x-y平面上點與xm-ym平面上點的關系

如圖10所示，將x-y-z坐標系中的x-y平面沿著z軸正方向平移r距離，使坐標系的原點o與銑刀球心重合，獲得新的坐標系xp-yp-zp。其中xp-yp-zp坐標系中的xp軸與x軸相互平行，且方向相同；yp軸與y軸相互平行，且方向相同；zp軸與z軸相互重合，且方向相同。

由xp-yp-zp坐標系獲得方式可知，xp-yp平面中的點(xp,yp)與x-y平面中的點(x,y)的關系為:

xp＝x，yp＝y(7)

如圖11所示，以xp軸為軸線，將yp-zp平面逆時針旋轉β度(xp軸正半軸向原點看，β值為正數，順時針；β值為負數，逆時針，以下以β為負值進行闡述)，旋轉之后，yp軸變為yf軸，zp軸變為zf軸，形成一個新的坐標系xf-yf-zf，其中xf與xp軸重合且方向相同。

由xf-yf-zf坐標系獲得方式可知，xp-yp-zp坐標系中點(xp,yp,zp)與xf-yf-zf坐標系中的點(xf,yf,zf)關系為：

令zf＝zp＝0，則可得：

xf＝xp，yf＝ypcosβ(8)

如圖12所示，將坐標系xf-yf-zf中的xf-yf平面沿著zf負方向平移r距離，得到xm-ym-zm坐標系，其中，xm軸與xf軸相互平行，且方向相同；ym軸與yf軸相互平行，且方向相同；zm軸與zf軸相互重合，且方向相同。如圖13所示，xm-ym-zm坐標系的原點就是前傾角為α度，側傾角為β度時球頭銑刀的頂點，zm軸就是前傾角為α度，側傾角為β度時球頭銑刀的軸線，a，b，c，d四條邊界的求解問題轉化為它們在xm-ym平面的投影方程的求解問題。

由xm-ym-zm坐標系獲得方式，可知xm-ym平面中的點(xm,ym)與xf-yf平面中的點(xf,yf)的關系為：

xm＝xf，ym＝yf(9)

由公式(7)，(8)和(9)可得x-y平面上點與xm-ym平面上點的關系：

xm＝x，ym＝ycosβ(10)

經過以上推導可知，前傾角為α度，側傾角為零度時和前傾角為α度，側傾角為β度時，銑刀球頭的位置并沒有變化，刀觸點沒有變化，只是刀軸線變化了，刀位點發生了變化，也即目標坐標系由x-y-z變成了xm-ym-zm，這主要是由銑刀球頭的幾何特性所形成的。

由式(10)可知xm-ym平面上點與x-y平面上點的關系，因此，a，b，c，d四條線邊界曲線在xm-ym坐標系下的投影方程的求解問題可以轉化為這四條線邊界線在x-y坐標系下的投影方程的求解問題。

3.5確定a，b，c，d，e四條線在x-y坐標系下的投影方程

3.5.1a號線在x-y坐標系下投影方程求解過程

a號線為銑刀球頭與工件加工表面的交線。如圖8所示，工件加工表面在x-y-z坐標系下的方程需要通過x0-y0-z0坐標系與x-y-z坐標系關系的獲得。

如圖9所示，在x0-z0坐標系下，在工件加工表面任取a(xa0,za0)、b(xb0,zb0)兩點，由于工件加工面為平面，故za0＝zb0＝l_jg。通過x–z坐標系與x0-z0坐標系的關系，可獲得a、b兩點在x–z坐標系的值(xa,za)，(xb,zb)，具體獲取方式如下：

獲取a、b在x–z坐標系下坐標之后，計算出經過a、b兩點在x–z坐標系下的直線方程z＝kx+b，其中此方程在x–z坐標系下為直線方程，在x-y-z下可表示為工件加工表面方程。

在x-y-z下，將工件加工表面方程z＝kx+b與銑刀球頭方程x²+y²+(z-r)²＝r²方程聯立，即可得到a號線在x-y二維坐標系下投影方程x²+y²+(kx+b-r)²＝r²。

3.5.2b號線投影方程求解過程

b號線為球頭銑刀垂直于進給方向的輪廓圓截面與工件過渡表面的交線，如圖14所示，此圓投影到x-y二維坐標系下為一橢圓，橢圓方程為

3.5.3c號線投影方程求解過程

c號線為本次走刀與上一次走刀在工件已加工表面留下的加工殘余而形成的線，如圖15所示，在y1-z1坐標系下，獲得銑刀球頭投影方程y1²+(z1-r)²＝r²，將其沿著y1負方向平移l_xl，得到方程(y1+l_xl)²+(z1-r)²＝r²，即為與本次刀觸點相對應的上一次加工時的銑刀球頭輪廓方程。兩圓交點m所對的y1值為-l_xl/2，即為c號線在x1-y1二維坐標系下的投影，由于x-y-z坐標系與x1-y1-z1坐標系的x-z平面與x1-z1平面相重合，y軸與y1軸相互投影方程平行，故c號線在x-y二維坐標系下的投影方程為y＝-l_xl/2。

3.5.4d號線求解過程

d號線投影方程求解過程同a號和e號線投影方程有關，在求解d號線投影方程之前，先確定e號線投影方程。

1)e號線投影方程求解過程

e號線為上一次走刀在工件加工表面留下的加工痕跡。如圖15所示，在y1-z1坐標系下，將z1＝l_jg帶入到與本次刀位點相對應的上一次加工時的銑刀球頭輪廓方程(y1+l_xl)²+(z1-r)²＝r²中，得到的最大的y1即為e號線在x1-y1坐標系下的投影，經計算該值為由于x-y-z坐標系與x1-y1-z1坐標系中的x-z平面與x1-z1平面相重合，y軸與y1軸相互平行，因此，e號線在x-y二維坐標系下的投影方程為

2)d號線投影方程求解過程

圖16中的d號線上的n點在x-y坐標系下的投影可由a號線和e號線在x-y坐標系下投影方程聯立得到，經計算n點x值滿足方程y值為

利用分層思想可知，d號線上的其它點可以認為是不同軸向切削深度所對應的a號線與e號的交點，因此將n點坐標中的l_jg用變量k_v替換，可得單純從數學角度觀察n點坐標，可知：在其它值一定的情況下，n點的坐標值只與變量k_v值有關，改變k_v值，就能得到d號線上其它點的投影坐標。

如圖17示，k_v最大取值為l_jg，最小取值為e號線在y1-z1坐標系投影所對應的z1坐標，即m點所對用的z1值為了精準表示d號線投影方程，決定在x-y平面上沿y軸等間距在d號線投影上取7個點的坐標值，具體如下所示：

如圖17所示，d號線在x1-y1平面投影所對應的最大y1值為最小y1值為從y1的最大值和最小值中等間距取7值，通過方程(x大于零的解)和獲取7組所對應的x，y值，即可得到d號線在x-y平面上沿y軸等間距分布的7個點，對這7個坐標值進行牛頓插值即獲取如圖18所示的在x-y坐標系下的六次多項式方程。

3.6確定a，b，c，d在xm-ym坐標系下的投影方程

利用式(10)x＝xm，y＝ym/cosβ分別替換掉a，b，c，d在x-y坐標系下投影方程中的x，y，獲得的新的方程就是a，b，c，d在xm-ym坐標系下的投影方程，如圖19示，它們共同圍成的區域即為前傾角為α，側傾角為β時球頭銑刀與工件接觸區域在xm-ym坐標系下的投影。

步驟四、精細積分法對刀具-工件動力學方程時域數值求解

4.1精細積分法對刀具-工件動力學方程時域數值分解

由式(6)可將式(1)表示為如下形式：

將式(11)表示為如下所示的哈密頓系統：

其中，

將式(12)中a(t)v(t)-a(t)v(t-t)用f(t)來表示，則對于非齊次方程(12)，由常微分理論可知，一般解為：

將時滯周期t均分為m份，即t＝m·τ，在[tp,tp+1]中，將f(t)表示為如下形式：

f(t)＝r0+r1(t-tp)(14)

其中，r0＝f(tp)＝a(tp)v(tp)-a(tp)v(tp-m·τ)

由式(13)和式(14)可將v(tp+1)表示

v(tp+1)＝t·[v(tp)+a0^-1(r0+a0^-1r1)]-a0^-1(r0+a0^-1r1+r1·τ)(15)

其中，將ε均分為λ＝2²⁰份，則

由于足夠小，故用taylor展開式去近似表示為

由式(16)和式(17)可知，

因此，用n次矩陣相稱就能得到t中的非單位矩陣部分，即

將r0和r1進一步分別表示為

r0＝apvp-apvp-m(20)

將(20)和(21)帶入到式(15)中，可得：

其中，mm＝ta0^-1-a0^-1，nn＝ta0^-2-a0^-2-a0^-1τ

若(i-nn/τ·ap+1)可逆，則式(22)可表示為

其中，

4.2axx,p，axy,p，ayx,p，ayy,p和axx,p+1，axy,p+1，ayx,p+1，ayy,p+1確定方法

下面以nf＝2為例，來闡述axx,p，axy,p，ayx,p，ayy,p方法。在tp時刻，按照公式(2)將球頭銑刀全部切削刃投影到第三部分所建立的xm-ym坐標系下，其中n為刀具轉速，j從1到nf，k從0到π/2。

由銑刀刀齒數和構建出的刀具-工件的接觸區域可知在時滯周期內的任意時刻，只有一條切削刃參與切削，設此切削刃為第一條切削刃。如圖20所示，該切削刃在單齒切削周期內到達與b號線相切位置；b投影線與a投影線交點位置；與d號線相切位置；a投影線與d投影線交點位置；d投影線與c投影線交點位置；c投影線與b投影線交點位置；時滯周期切削結束的時刻分別記為t1，t2，t3，t4，t5，t6，t7。

當tp＝0時，如圖21所示，第一條切削刃沒有參與切削，當tp在0-t1時間內，如圖22所示，第一條切削刃沒有參與切削，此時kmax,1和kmin,1值都為零；當tp在t1-t2時間內，如圖23所示，第一條切削刃與b號線投影線相交，兩個交點所對應的軸向角的最大值即為tp時刻該切削刃在式(24)中所對應的kmax，1，最小值為tp時刻該切削刃在式(24)中所對應的kmin,1。同理，可以確定tp分別在t2-t3，t3-t4，t4-t5，t5-t6時間段內，第一條切削刃所對應kmax,1和kmin,1值，具體如圖24-圖27所示；當tp在t6-t7時間內，如圖28所示，第一條切削刃沒有參與切削，此時kmax,1和kmin,1值都為零。

確定出各個切削刃在tp參與切削的最大軸向角和最小軸向角之后，通過式(24)可得到axx,p，axy,p，ayx,p，ayy,p值。

通過以上步驟可以得到tp+1時刻時axx,p+1，axy,p+1，ayx,p+1，ayy,p+1值。

步驟五、葉瓣圖構建

5.1切削穩定性判定方法

建立系數矩陣cp，該矩陣滿足離散映射：

vp+1＝cpvp(25)

vp是個(2m+4)維的向量：

矩陣cp為(2m+4)維矩陣：

pk為4×4矩陣等于公式(23)中的(i-nn/τ·ap+1)^-1(t+mm·ap-nn/τ·ap)，rk1為4×2矩陣，等于式公式(23)中的-(i-nn/τ·ap+1)^-1nn/τ·ap+1的前兩列，rk2為4×2矩陣，等于式(23)中的(i-nn/τ·ap+1)^-1(nn/τ·ap-mm·ap)的前兩列。

通過使用一系列離散cp(p＝0,1,2…,m-1)，構建時滯周期t內的過渡矩陣φ，亦即：

vp＝φv0(28)

式中，φ定義為：φ＝cm-1cm-2…c1c0。

由floquet理論可知，傳遞函數φ所有特征值模的最大值小于1，等于1和大于1，分別表示在該刀具轉速n和軸向切深l_jg下，切削處于穩定狀態，臨界臨界狀態和不穩定狀態。

5.2葉瓣圖構建

主軸轉速不變，在[0,l_jg]范圍內不斷改變軸向切深，通過5.1中的方法，獲得該轉速下所對應的臨界軸向切深。改變軸向切深后的接觸區域投影邊界中只有a號線投影方程變化，b號線和c號線投影方程仍與l_jg時相同，具體如圖29所示。

改變主軸轉速，獲得不同主軸轉速在[0,l_jg]范圍內所對應的臨界軸向切深。最終，構建出臨界軸向切深隨主軸轉速變化的函數關系，即為顫振穩定域葉瓣圖，整個流程如圖30所示。