本發(fā)明涉及缺少測(cè)點(diǎn)的管網(wǎng)系統(tǒng)的管網(wǎng)單相流體水力數(shù)據(jù)獲取方法，屬于流體網(wǎng)絡(luò)水力的。

背景技術(shù)：

1、在實(shí)際的生產(chǎn)生活當(dāng)中，管道運(yùn)輸是最為常用、普遍且經(jīng)濟(jì)的運(yùn)輸方式。然而，在流體運(yùn)輸?shù)南嚓P(guān)進(jìn)程中，由于管道網(wǎng)絡(luò)錯(cuò)綜復(fù)雜，有效測(cè)點(diǎn)匱乏，并且針對(duì)水力熱力變化迅速的管道內(nèi)部流體，缺乏行之有效的監(jiān)測(cè)手段。

2、在理論研究領(lǐng)域以及精密的管道系統(tǒng)里，運(yùn)用流體網(wǎng)絡(luò)計(jì)算原理能夠精確算出管道水力數(shù)據(jù)。但在實(shí)際生產(chǎn)流程中，管道的內(nèi)部阻力系數(shù)以及手動(dòng)調(diào)節(jié)閥的閥門開(kāi)度和相關(guān)數(shù)據(jù)通常都是未知的，難以運(yùn)用常規(guī)的流體網(wǎng)絡(luò)理論來(lái)進(jìn)行計(jì)算。

3、近些年來(lái)，流體網(wǎng)絡(luò)理論的應(yīng)用不斷拓展和深化，但對(duì)于水力數(shù)據(jù)測(cè)點(diǎn)稀少或者變化迅速的管道系統(tǒng)的水力計(jì)算，往往無(wú)法借助理論計(jì)算來(lái)實(shí)現(xiàn)，故而現(xiàn)亟需一種方法來(lái)獲取內(nèi)部管道系統(tǒng)無(wú)測(cè)點(diǎn)的流體網(wǎng)絡(luò)的水力數(shù)據(jù)。

技術(shù)實(shí)現(xiàn)思路

1、為了解決上述存在的問(wèn)題，本發(fā)明公開(kāi)了一種缺少測(cè)點(diǎn)的管網(wǎng)系統(tǒng)的管網(wǎng)單相流體水力數(shù)據(jù)獲取方法，其具體技術(shù)方案如下：

2、一種缺少測(cè)點(diǎn)的管網(wǎng)系統(tǒng)的管網(wǎng)單相流體水力數(shù)據(jù)獲取方法，包括以下步驟：

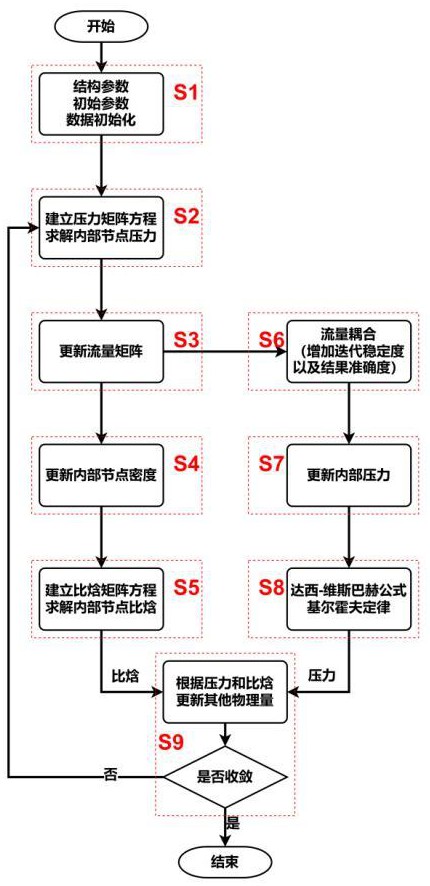
3、步驟s1，數(shù)據(jù)輸入與初始化：輸入流體網(wǎng)絡(luò)拓?fù)浣Y(jié)構(gòu)矩陣以及流體網(wǎng)絡(luò)原始邊界數(shù)據(jù)，對(duì)輸入數(shù)據(jù)進(jìn)行初始化處理；

4、步驟s2，設(shè)置迭代步長(zhǎng)并求解壓力矩陣：設(shè)置迭代步長(zhǎng)后進(jìn)入迭代循環(huán)，將步驟s1中獲得數(shù)據(jù)，根據(jù)質(zhì)量守恒公式以及動(dòng)量守恒公式聯(lián)立求解，構(gòu)造出壓力矩陣方程，運(yùn)用lu?分解法求解壓力矩陣；

5、步驟s3，求解新的內(nèi)部流量矩陣：將步驟s2得到的壓力矩陣的求解數(shù)據(jù)，與步驟s1的數(shù)據(jù)代入流線動(dòng)量方程進(jìn)行求解，得出新的內(nèi)部流量矩陣；

6、步驟s4，更新內(nèi)部節(jié)點(diǎn)密度數(shù)組：根據(jù)步驟s3得到的內(nèi)部流量矩陣，結(jié)合步驟s1中數(shù)據(jù)，代入質(zhì)量守恒公式求解，進(jìn)而得到更新后的內(nèi)部節(jié)點(diǎn)密度數(shù)組；

7、步驟s5，求解更新后的內(nèi)部節(jié)點(diǎn)比焓數(shù)組：把步驟s4中得到的內(nèi)部節(jié)點(diǎn)密度數(shù)組，與步驟s1步驟中得到的數(shù)據(jù)代入能量守恒公式，構(gòu)造比焓矩陣方程，再利用?lu?分解法求解比焓矩陣方程，獲得更新后的內(nèi)部節(jié)點(diǎn)比焓數(shù)組；

8、步驟s6，調(diào)整內(nèi)部流量矩陣：把步驟s3中迭代后得到的內(nèi)部流量矩陣與步驟s1中的初始內(nèi)部流量矩陣相加并求平均值，得到新的內(nèi)部流量矩陣；

9、步驟s7，更新節(jié)點(diǎn)壓力數(shù)組：根據(jù)基爾霍夫定律以及達(dá)西-威斯巴赫公式逐項(xiàng)更新壓力；

10、步驟s8，更新密度數(shù)組與阻力矩陣：更新得到新的內(nèi)部阻力矩陣和邊界阻力矩陣；

11、步驟s9，判斷迭代是否結(jié)束：判斷壓力是否收斂，收斂則結(jié)束，未收斂返回步驟s2。

12、進(jìn)一步的，所述步驟s1中，流體網(wǎng)絡(luò)原始邊界數(shù)據(jù)包括節(jié)點(diǎn)溫度數(shù)據(jù)、邊界節(jié)點(diǎn)流量或壓力數(shù)據(jù)、內(nèi)部節(jié)點(diǎn)管長(zhǎng)管徑數(shù)據(jù)以及入口壓力；

13、對(duì)輸入數(shù)據(jù)進(jìn)行初始化處理具體為：依據(jù)流體網(wǎng)絡(luò)拓?fù)渚仃嚕瑢⒋蠊?jié)點(diǎn)數(shù)據(jù)與整體數(shù)據(jù)進(jìn)行向量化處理，把流線數(shù)據(jù)進(jìn)行矩陣化處理；借助?iapws?水蒸汽庫(kù)，通過(guò)初始?jí)毫εc溫度對(duì)其他初始數(shù)據(jù)進(jìn)行計(jì)算求解；最終得到10組向量數(shù)據(jù)，即內(nèi)部節(jié)點(diǎn)溫度數(shù)組、邊界節(jié)點(diǎn)溫度數(shù)組、內(nèi)部節(jié)點(diǎn)壓力數(shù)組、邊界節(jié)點(diǎn)壓力數(shù)組、內(nèi)部節(jié)點(diǎn)比焓數(shù)組、邊界節(jié)點(diǎn)比焓數(shù)組、內(nèi)部節(jié)點(diǎn)管長(zhǎng)數(shù)組、內(nèi)部節(jié)點(diǎn)管徑數(shù)組、內(nèi)部節(jié)點(diǎn)密度數(shù)組、邊界節(jié)點(diǎn)密度數(shù)組；5?組矩陣數(shù)據(jù)，分別為內(nèi)部流量矩陣、邊界流量矩陣、內(nèi)部阻力矩陣、邊界阻力矩陣、流體網(wǎng)絡(luò)拓?fù)渚仃嚕灰约?1?個(gè)數(shù)值數(shù)據(jù)，即入口壓力數(shù)值。

14、進(jìn)一步的，所述步驟s1中，根據(jù)流體網(wǎng)絡(luò)理論對(duì)需要計(jì)算的管網(wǎng)進(jìn)行建模，得到流體網(wǎng)絡(luò)拓?fù)渚仃嚕痪唧w過(guò)程為：將一段管道視為一個(gè)內(nèi)部節(jié)點(diǎn)，管道系統(tǒng)邊界與系統(tǒng)外連接的位置設(shè)為邊界節(jié)點(diǎn)，邊界節(jié)點(diǎn)有溫度、壓力數(shù)據(jù)，但沒(méi)有實(shí)體，所以不存在管長(zhǎng)管徑數(shù)據(jù)，節(jié)點(diǎn)之間通過(guò)流線連接，流線代表管道之間的流體流動(dòng)關(guān)系，由此得到流體網(wǎng)絡(luò)拓?fù)渚仃嚕黧w網(wǎng)絡(luò)矩陣包括內(nèi)部拓?fù)渚仃嚭瓦吔缤負(fù)渚仃嚕瑢?shí)際使用時(shí)合并稱為流體網(wǎng)絡(luò)拓?fù)渚仃嚕粌?nèi)部拓?fù)渚仃嚧笮?n×n，n為內(nèi)部節(jié)點(diǎn)個(gè)數(shù)；邊界拓?fù)渚仃嚧笮?n×m，n為內(nèi)部節(jié)點(diǎn)個(gè)數(shù)，m為邊界節(jié)點(diǎn)個(gè)數(shù)；內(nèi)部節(jié)點(diǎn)拓?fù)潢P(guān)系矩陣的值有三種情況：0表示節(jié)點(diǎn)i與節(jié)點(diǎn)j沒(méi)有流線連接；-1表示流線方向?yàn)橛蒳流向j；1表示流線方向?yàn)橛蒵流向i；步驟s1中構(gòu)造的數(shù)組，與內(nèi)部節(jié)點(diǎn)相關(guān)的數(shù)組大小為n，與邊界節(jié)點(diǎn)相關(guān)的數(shù)組大小為m；步驟s1中構(gòu)造的矩陣，與內(nèi)部相關(guān)的矩陣大小為n×n，與邊界相關(guān)的矩陣大小為?n×m。

15、進(jìn)一步的，所述步驟s2中，將步驟s1中獲得的內(nèi)部節(jié)點(diǎn)壓力數(shù)組、邊界節(jié)點(diǎn)壓力數(shù)組、流體網(wǎng)絡(luò)拓?fù)渚仃嚒?nèi)部流量矩陣和邊界流量矩陣這?5?組數(shù)據(jù)，根據(jù)質(zhì)量守恒公式以及動(dòng)量守恒公式聯(lián)立求解，構(gòu)造出壓力矩陣方程，運(yùn)用?lu?分解法求解壓力矩陣，從而得到更新后的內(nèi)部節(jié)點(diǎn)壓力數(shù)組，具體過(guò)程為：

16、質(zhì)量守恒公式為：

17、，

18、其中，v是節(jié)點(diǎn)體積，是節(jié)點(diǎn)密度，t是時(shí)間，內(nèi)部節(jié)點(diǎn)拓?fù)潢P(guān)系矩陣，是邊界拓?fù)潢P(guān)系矩陣，是內(nèi)部流量矩陣，是邊界流量矩陣，n是內(nèi)部節(jié)點(diǎn)個(gè)數(shù)，m是外部節(jié)點(diǎn)個(gè)數(shù)，i、j、k均為節(jié)點(diǎn)編號(hào)，下標(biāo)ij代表內(nèi)部節(jié)點(diǎn)i與內(nèi)部節(jié)點(diǎn)j的關(guān)系，下標(biāo)ik代表內(nèi)部節(jié)點(diǎn)i與邊界節(jié)點(diǎn)k的關(guān)系；

19、動(dòng)量守恒公式為：

20、，

21、其中，i為結(jié)構(gòu)參數(shù)，是內(nèi)部流量矩陣，是內(nèi)部拓?fù)渚仃嚕琾代表節(jié)點(diǎn)壓力，h為動(dòng)力源項(xiàng)，f為流線阻力項(xiàng)；計(jì)算時(shí)，設(shè)定流動(dòng)過(guò)程是穩(wěn)定的，流量不會(huì)忽大忽小，即，流動(dòng)過(guò)程為穩(wěn)態(tài)，則i為0，將質(zhì)量守恒公式和動(dòng)量守恒公式聯(lián)立展開(kāi)得到壓力矩陣方程：

22、，

23、其中，r代表內(nèi)部節(jié)點(diǎn)達(dá)西阻力系數(shù)，re代表邊界節(jié)點(diǎn)達(dá)西阻力系數(shù)，g為內(nèi)部流量矩陣，ge為邊界流量矩陣，p為內(nèi)部節(jié)點(diǎn)壓力，pe為邊界節(jié)點(diǎn)壓力，t+1為t的下一迭代時(shí)間。

24、進(jìn)一步的，所述步驟s3中，將步驟s2得到的內(nèi)部節(jié)點(diǎn)壓力數(shù)組，與步驟s1中的內(nèi)部阻力矩陣、邊界阻力矩陣以及流體網(wǎng)絡(luò)拓?fù)渚仃囘@4組數(shù)據(jù)，代入流線動(dòng)量方程進(jìn)行求解，得出新的內(nèi)部流量矩陣；

25、所述步驟s4中，根據(jù)步驟s3得到的內(nèi)部流量矩陣，結(jié)合步驟s1中獲取的內(nèi)部節(jié)點(diǎn)管長(zhǎng)數(shù)組、內(nèi)部節(jié)點(diǎn)管徑數(shù)組、內(nèi)部節(jié)點(diǎn)密度數(shù)組以及邊界流量矩陣，代入質(zhì)量守恒公式求解，進(jìn)而得到更新后的內(nèi)部節(jié)點(diǎn)密度數(shù)組。

26、進(jìn)一步的，所述步驟s5中，把步驟s4中得到的內(nèi)部節(jié)點(diǎn)密度數(shù)組，與步驟s1中得到的內(nèi)部節(jié)點(diǎn)管長(zhǎng)數(shù)組、內(nèi)部節(jié)點(diǎn)管徑數(shù)組、內(nèi)部流量矩陣、邊界流量矩陣代入能量守恒公式，能量守恒公式為：

27、，

28、其中，v是節(jié)點(diǎn)體積，是節(jié)點(diǎn)密度，是內(nèi)部拓?fù)渚仃嚕沁吔缤負(fù)渚仃嚕莾?nèi)部流量矩陣，是邊界流量矩陣，h是內(nèi)部節(jié)點(diǎn)比焓，是邊界節(jié)點(diǎn)比焓,s是源項(xiàng)。

29、進(jìn)一步的，所述步驟s7具體為：

30、依據(jù)步驟s1中的流體網(wǎng)絡(luò)拓?fù)渚仃嚧_定節(jié)點(diǎn)的流向，將步驟s1中的入口壓力數(shù)值作為管道網(wǎng)絡(luò)的起點(diǎn)，利用步驟s6得到的內(nèi)部流量矩陣，以及步驟s1中的內(nèi)部阻力矩陣、邊界阻力矩陣代入達(dá)西-威斯巴赫公式，求解出節(jié)點(diǎn)之間的壓力差，再運(yùn)用基爾霍夫定律，從流體網(wǎng)絡(luò)的起點(diǎn)開(kāi)始，按照節(jié)點(diǎn)之間流線的流向逐個(gè)更新節(jié)點(diǎn)的壓力值，最終得到新的內(nèi)部節(jié)點(diǎn)壓力數(shù)組以及邊界節(jié)點(diǎn)壓力數(shù)組；

31、達(dá)西?-?威斯巴赫公式為：

32、，

33、其中，是沿程水頭損失，f是摩擦系數(shù)，l是管道長(zhǎng)度，d是管道直徑，v是流體的平均流速，g是重力加速度。

34、進(jìn)一步的，所述步驟s8具體為：

35、根據(jù)步驟s7獲得的內(nèi)部節(jié)點(diǎn)壓力數(shù)組和邊界節(jié)點(diǎn)壓力數(shù)組、步驟s5獲得的內(nèi)部節(jié)點(diǎn)比焓數(shù)組、步驟s1獲得的內(nèi)部節(jié)點(diǎn)管長(zhǎng)數(shù)組、內(nèi)部節(jié)點(diǎn)管徑數(shù)組、流體網(wǎng)絡(luò)拓?fù)渚仃嚕柚?iapws?水蒸汽數(shù)據(jù)庫(kù)進(jìn)行數(shù)值計(jì)算，并利用流體網(wǎng)絡(luò)拓?fù)渚仃囘M(jìn)行結(jié)構(gòu)構(gòu)造，得到新的內(nèi)部節(jié)點(diǎn)密度數(shù)組，同時(shí)，根據(jù)達(dá)西-威斯巴赫公式重新計(jì)算節(jié)點(diǎn)阻力系數(shù)，進(jìn)而得到新的內(nèi)部阻力矩陣和邊界阻力矩陣。

36、進(jìn)一步的，所述步驟s9具體為：

37、通過(guò)計(jì)算進(jìn)入步驟s2的初始內(nèi)部節(jié)點(diǎn)壓力數(shù)組與步驟s7中更新后的內(nèi)部節(jié)點(diǎn)壓力數(shù)組的殘差絕對(duì)值數(shù)組，若殘差數(shù)組的每一項(xiàng)均小于設(shè)定值，則結(jié)束循環(huán)；否則，將步驟s7中的內(nèi)部節(jié)點(diǎn)壓力數(shù)組、邊界節(jié)點(diǎn)壓力數(shù)組，步驟s5獲得的內(nèi)部節(jié)點(diǎn)比焓數(shù)組，步驟s8中的內(nèi)部節(jié)點(diǎn)密度數(shù)組、內(nèi)部阻力矩陣和邊界阻力矩陣，步驟s1中內(nèi)部節(jié)點(diǎn)溫度數(shù)組、邊界節(jié)點(diǎn)溫度數(shù)組、內(nèi)部節(jié)點(diǎn)管長(zhǎng)數(shù)組、內(nèi)部節(jié)點(diǎn)管徑數(shù)組、邊界節(jié)點(diǎn)比焓數(shù)組、流體網(wǎng)絡(luò)拓?fù)渚仃嚕约叭肟趬毫?shù)值作為初始值，返回步驟s2繼續(xù)進(jìn)行計(jì)算。

38、本發(fā)明的有益效果是：

39、本發(fā)明理論基礎(chǔ)創(chuàng)新：本算法以流體網(wǎng)絡(luò)理論為基石，突破了傳統(tǒng)算法的計(jì)算局限，為復(fù)雜管道系統(tǒng)的流體水力數(shù)據(jù)處理提供了全新的思路和方法。

40、本發(fā)明數(shù)據(jù)適應(yīng)性增強(qiáng)：本算法能夠在測(cè)點(diǎn)較少、管道內(nèi)部阻力系數(shù)未知、管道閥門開(kāi)度數(shù)據(jù)以及閥門關(guān)系無(wú)法獲取的情況下，依然有效地對(duì)管道系統(tǒng)的流體水力數(shù)據(jù)進(jìn)行模擬預(yù)測(cè)，大幅拓展了算法的適用范圍。

41、本發(fā)明預(yù)測(cè)能力提升：在面對(duì)上述諸多數(shù)據(jù)缺失和不確定性的困境時(shí)，本發(fā)明展現(xiàn)出出色的模擬預(yù)測(cè)能力，顯著提高了流體水力數(shù)據(jù)預(yù)測(cè)的準(zhǔn)確性和可靠性，為相關(guān)決策提供了有力支撐。