本發明涉及橋梁工程，具體涉及一種uhpc組合梁截面應力分布計算及繪制方法、系統及存儲介質。

背景技術：

1、隨著超高性能混凝土（uhpc）的發展和應用，uhpc-鋼組合梁因其優異的力學性能在橋梁工程中得到廣泛應用。準確計算組合梁截面的應力分布對于結構設計和性能評估具有重要意義。

2、目前，已公開的技術中，申請號為cn202311748675.x的中國專利申請公開了一種采用多種pbl連接件混合連接的鋼-uhpc組合梁及其設計方法，其中提出了一種基于受彎極限狀態的組合梁設計方法，但未充分考慮uhpc的應變硬化特性；申請號為cn202411139448.1的中國專利申請公開了一種高強鋼-uhpc組合梁抗彎承載力確定方法，其中提出了考慮材料非線性的計算方法，但計算過程復雜，且無法明確uhpc-鋼組合梁全過程受力的截面應力分布情況。

3、雖然，現有技術中對于uhpc-鋼組合梁的受力分析提供了多種不同的方式，但是普遍存在以下問題：1）由于uhpc材料具有顯著的非線性特性，特別是在受拉區表現出應變硬化行為，傳統的線彈性計算方法難以準確反映其真實受力狀態；2）在求解中性軸位置時，常規迭代算法容易出現振蕩發散，收斂性差；3）無法明確uhpc-鋼組合梁全過程受力的截面應力分布情況。

4、掌握uhpc-鋼組合梁截面應力分布及計算，可以得到在受力過程中型鋼屈服、鋼筋屈服、uhpc開裂、uhpc壓潰等受力特征點，明確組合截面在受力過程中達到這些特征點的先后順序，從而指導uhpc-鋼組合梁的結構受力計算和截面布置優化。因此，急需一種uhpc組合梁截面應力分布計算及繪制方法、系統及存儲介質以解決現有技術中存在的問題。

技術實現思路

1、本發明目的在于提供一種uhpc組合梁截面應力分布計算及繪制方法，旨在解決現有技術無法明確uhpc-鋼組合梁受力過程中的截面應力分布的問題，具體技術方案如下：

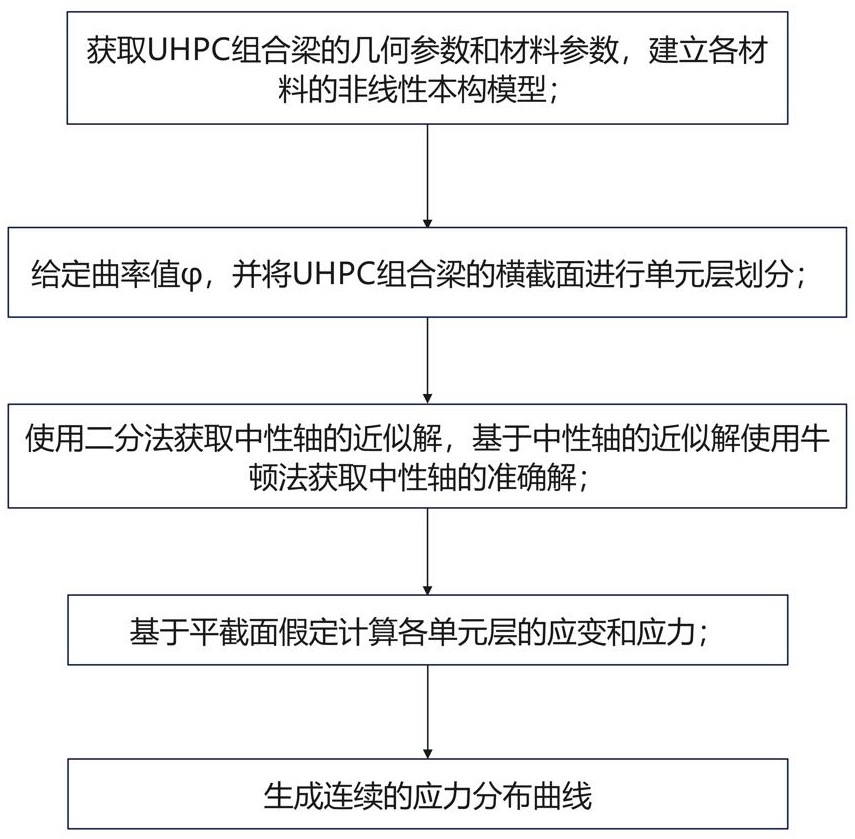
2、一種uhpc組合梁截面應力分布計算及繪制方法，包括：

3、s1、獲取uhpc組合梁的幾何參數和材料參數，建立各材料的非線性本構模型；

4、s2、給定曲率值 φ，并將uhpc組合梁的橫截面進行單元層劃分；

5、s3、使用二分法獲取中性軸的近似解，基于中性軸的近似解使用牛頓法獲取中性軸的準確解；

6、s4、基于平截面假定計算各單元層的應變和應力；

7、s5、根據各單元層的應力生成連續的應力分布曲線。

8、優選的，采用二分法獲取中性軸的近似解，具體是：

9、a1、設定初始搜索區間為[ a, b]?=?[0, h]，其中 h為uhpc組合梁的橫截面總高度；

10、a2、計算中性軸位于 a處時的截面總軸力以及位于 b處時的截面總軸力；

11、a3、若則說明當前搜索區間內沒有解，結束計算；若則進入步驟a4；

12、a4、計算當前搜索區間的中點，并計算中性軸位于 c處時的截面總軸力；

13、a5、若滿足或，則輸出當前搜索區間的中點 c為中性軸的近似解，否則進行搜索區間更新后重復步驟a2-a5；

14、其中，為二分法中設置的收斂容差，為區間長度收斂閾值；步驟a5中更新搜索區間的方式具體是：若是，則令以更新搜索區間；若是，則令以更新搜索區間。

15、優選的，采用牛頓法獲取準確解，具體步驟如下：

16、b1、取，令；

17、b2、計算中性軸在時的截面總軸力；

18、b3、若滿足，則輸出當前的為中性軸位置的準確解；若不滿足則判斷當前的是否小于 n，若小于則進入步驟b4，若不小于則結束計算；其中， n為最大迭代次數，為牛頓法中設置的收斂容差，；

19、b4、計算獲得當前截面總軸力的導數；

20、b5、更新中性軸位置為，并且令后重復步驟b2；其中，為第次迭代時的松弛因子。

21、優選的，所述松弛因子根據迭代的軸力誤差進行動態調整，表示為：

22、???????????????????（3），

23、其中，所述軸力誤差表示為：

24、?????????????（4），

25、其中：為第次迭代獲得的截面總軸力；表示第次迭代時的松弛因子；為調整系數，若相鄰兩次的軸力誤差呈減小趨勢時取大于1，若相鄰兩次軸力誤差呈增大趨勢時取小于1，若相鄰兩次軸力誤差相等則取等于1。

26、優選的，截面總軸力的計算方式具體如下：

27、根據曲率和設定的中性軸位置，基于平截面假定得到橫截面中各單元層的應變；

28、根據材料的非線性本構模型和各單元層的應變，計算獲得各單元層的應力；

29、根據各單元層的應力和面積計算uhpc組合梁橫截面內的總軸力。

30、優選的，對uhpc組合梁的橫截面進行單元層劃分具體是：

31、對uhpc組合梁的uhpc混凝土的橫截面以及t型鋼梁位于uhpc混凝土之外部分的橫截面分別進行單元層劃分，同時，將uhpc組合梁最上層的所有縱向鋼筋的橫截面以及uhpc組合梁最底層的所有縱向鋼筋的橫截面分別作為一個單元層。

32、優選的，uhpc混凝土的非線性本構模型為：

33、????（1），

34、其中，為uhpc混凝土的應變，為uhpc混凝土的應力，為uhpc混凝土的彈性模量；為uhpc混凝土的受壓極限應變；為uhpc混凝土的受拉彈性極限應變；為uhpc混凝土的受拉極限應變；為uhpc混凝土的斷裂應變；為uhpc混凝土的受拉彈性極限應力；為uhpc混凝土的受拉極限應力。

35、優選的，uhpc組合梁中t型鋼梁和鋼筋的非線性本構模型均為：

36、????（2），

37、其中，為t型鋼梁或鋼筋的應變，為t型鋼梁或鋼筋的應力，為t型鋼梁或鋼筋的彈性模量；為t型鋼梁或鋼筋的受壓極限應變；為t型鋼梁或鋼筋的抗拉屈服應變；為t型鋼梁或鋼筋的應變硬化起始應變；為t型鋼梁或鋼筋的極限拉應變；若無屈服平臺，則；為t型鋼梁或鋼筋的屈服應力；為t型鋼梁或鋼筋的極限拉應力。

38、本發明還提供了一種uhpc組合梁截面應力分布計算及繪制系統，該系統采用上述的uhpc組合梁截面應力分布計算及繪制方法，該系統包括：

39、參數輸入模塊，用于輸入幾何參數、材料參數和計算控制參數；其中計算控制參數包括收斂容差和、區間長度收斂閾值、最大迭代次數 n、初始的松弛因子和初始的調整系數；

40、網格剖分模塊，用于將uhpc組合梁的橫截面進行單元層劃分；

41、迭代計算模塊，使用二分法獲取中性軸的近似解，基于中性軸的近似解使用牛頓法獲取中性軸的準確解；

42、應力計算模塊，用于計算各單元層的應變和應力；

43、結果處理模塊，用于生成連續的應力分布曲線。

44、本發明還提供了一種存儲介質，所述存儲介質中存儲有計算機程序，所述計算機程序運行時執行所述的uhpc組合梁截面應力分布計算及繪制方法。

45、應用本發明的技術方案，具有以下有益效果：

46、本發明的方法采用uhpc混凝土非線性本構模型，考慮了uhpc的應變硬化特性，可以準確反映其真實受力狀態，為后續的計算提供準確的分析基礎；通過本發明的方法可以獲得uhpc組合梁在不同曲率下（通過給定不同的曲率值）的應力分布曲線，即通過本發明的方法可以獲取uhpc組合梁在各典型受力情況下的應力分布情況，得到在受力過程中型鋼屈服、鋼筋屈服、uhpc開裂、uhpc壓潰等受力特征點，明確組合截面在受力過程中達到這些特征點的先后順序，從而指導uhpc組合梁的結構受力計算和截面布置優化，保證uhpc組合梁的安全設計。

47、本發明的方法通過二分法初次獲取中性軸位置的近似解，然后通過牛頓法獲取中性軸位置的準確解，可以快速計算獲得準確的中性軸位置，為后續的應力和應變計算提供準確的數據基礎，解決了常規迭代算法容易出現振蕩發散，收斂性差的問題。

48、除了上面所描述的目的、特征和優點之外，本發明還有其它的目的、特征和優點。下面將參照圖，對本發明作進一步詳細的說明。