本發明屬于高速鐵路牽引供電電能質量分析領域，具體涉及一種分析低頻調制信號在HXD型機車整流器傳播規律的方法。

背景技術：

HXD、EMUs是典型的非線性負荷，在采用“交-直-交”方式后較好地克服了功率因數較低的缺點。然而大量電力機車升弓取流整備時，使得牽引網網壓較大波動，導致機車繼保裝置動作，IGBT出現自鎖，甚至引發運輸癱瘓。現場通過電力列車漸進式升弓方式來抑制該問題，但無法從根本上解決問題。

針對該現象，研究均從低頻振蕩角度研究牽引網電氣量不穩定問題。電力系統中低頻振蕩問題主要表征為擾動下發電機轉子間的相互搖擺，在缺乏阻尼時引起的持續振蕩。目前，針對低頻振蕩產生機理主要有：負阻尼機理、強迫振蕩機理和混沌理論。此外，現有技術還研究了電網鏈式分布、區域間功率不平衡等對電力系統低頻振蕩進行阻尼影響分析。考慮牽引供電系統拓撲結構的特殊性、負載的隨機性及非線性，與理論分析的對象、產生過程及數學建模均存在差異，因而不可以簡單地歸結為低頻振蕩問題，需深入挖掘牽引網實際監測數據的隱含信息。

技術實現要素：

本發明所要解決的技術問題是提供一種分析低頻調制信號在HXD型機車整流器傳播規律的方法，準確定位牽引網電壓波動的特征；對維護高速鐵路牽引供電系統的安全穩定運行具有非常重要的實際工程意義。

為解決上述技術問題，本發明采用的技術方案是：

一種分析低頻調制信號在HXD型機車整流器傳播規律的方法，包括以下步驟：

步驟1：利用DFT變換與TLS-ESPRIT結合的方法對牽引網、機車中間直流環節實際監測數據的隱含信息進行挖掘，確定網側、中間直流側引發波動的具體模態，網壓頻率信號與整流器中間直流電壓頻率成份的關系為：

式中，u_ab為機車整流器輸入端電壓；U_kr和b_kr分別表示整流器輸出調制信號電壓的幅值和諧波能量系數，k＝1，2，3…，U_dc為整流器輸出電壓中的直流電壓分量；

步驟2：構建在步驟1所示模態下的牽引網網壓波動信號的數學模型：

式中，m_i、m_hj為基波、諧波的調制系數，其取值范圍為0～1；表示基波的初始相位角；f_hj和分別表示諧波頻率和初始相位；

步驟3：再利用步驟2中所構造出的數學模型，推導其在SPWM算法下的傳播機理為：

式中，S_(t)表示整流器開關函數，N表示電壓量含有的總諧波次數。

與現有技術相比，本發明的有益效果是：

1.針對多車接入牽引供電系統引發的電氣量不穩定問題，本發明使用DFT與TLS-ESPRIT相結合的方法確定了牽引網電氣量不穩定現象并非低頻振蕩問題，而是電能質量電壓波動問題；并對其主導模態給出準確辨識結果；

2.從數學推導的角度，明確了整流器兩端的諧波傳遞的數學關系，為電壓波動的有效抑制奠定了理論基礎。

附圖說明

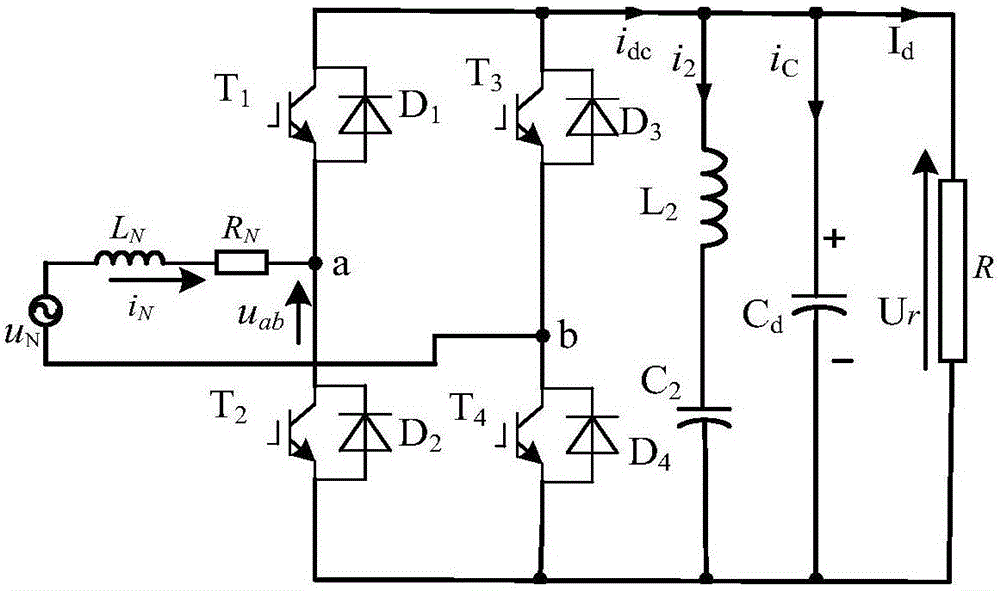
圖1是HXD型電力機車單相兩電平脈沖整流器主電路。

圖2是網側牽引變流器開關函數圖。

具體實施方式

下面結合附圖和具體實施方式對本發明作進一步詳細的說明。本發明方法的分析對象為多車接入牽引網引發牽引網電壓波動現象，主要實現步驟為：深入挖掘牽引網、機車中間直流環節實際監測數據的隱含信息，量化二者關系，并與低頻調制信號在整流器中傳播規律進行對比驗證，其主要步驟包括以下幾個方面：

1、使用DFT變換與TLS-ESPRIT結合的方法，分析的牽引網不穩定電氣量模態成份；

構造多車接入牽引供電系統時的電壓信號u(n)，Hankel矩陣X

式中，α_i、ω_i、A_i、θ_i分別為第i模式的衰減系數、角頻率、振蕩幅值和初相位；T_s為信號的采樣周期；p為信號階數，一般為實際正弦分量個數的兩倍；w(n)為白噪聲；稱為該信號的極點；N為u的數據個數，M＝N/2，L＝N-M+1。

對X進行奇異值分解X＝UΣV^T，并確定信號子空間階數p，構造矩陣[V₁V₂]，求取總體最小二乘解為

求矩陣Ψ_Tls的特征值λ_i(i＝1,2,……,p)，計算模式的頻率和阻尼比

隨后通過構造矩陣、擬合系數計算模式的幅值和初相位，進行主導模式篩選；采用頻率比對的方式，確定信號的模態成份。同理，對整流器中間直流電壓進行處理。結果網壓頻率信號與整流器中間直流電壓頻率成份存在如下關系：

式中，u_ab為機車整流器輸入端電壓；U_kr和b_kr分別表示整流器輸出調制信號電壓的幅值和諧波能量系數，k＝1,2,3…，U_dc為整流器輸出電壓中的直流電壓分量。

2、考慮該現象中高次諧波成份也出現被調制現象，構造電壓波動信號表示為

式中，m_i、m_hj為基波、諧波的調制系數，其取值范圍為0～1；表示基波的初始相位角；f_hj和分別表示諧波頻率和初始相位。

3、結合構造的數學模型，機車整流器電路如圖1所示，為便于分析，定義理想開關函數S_a和S_b并忽略牽引繞組電阻，由于上橋臂與下橋臂不允許直通，則在每相橋臂中，上橋臂的開關信號必須與下橋臂的開關信號互反。采用雙極性SPWM算法，開關函數如圖2所示，輸入端電壓u_ab的取值有U_d、0、-U_d三種電平，有效的開關組合有2²＝4種，即S_ab＝00、01、10、11四種邏輯。當調制波電壓大于載波電壓時，S_A為1，否則為0。b相與a相調制方式相同，但b相調制波與a相調制波相位相差180°。本發明分析的牽引變流器開關函數為：

式中，J_n(x)為貝塞爾函數；ω_m為調制信號角頻率；ω_c為載波信號角頻率；p為調制波與載波頻率比例系數(載波比的倒數)；ε為采樣系數，取值一般為0～1；M為調制系數，其取值范圍為0～1。

忽略諧波間的相互影響，則式(5)可簡化如下：

整理后得

式(7)為牽引供電系統側調制電壓的表達式，該表達式可以準確反映出牽引供電系統側電壓受到調制的頻譜特征。顯然，式(7)中第一項為基波和一系列特征諧波之和，其為整流開關函數對整流器輸出電壓中直流電壓分量U_dc的調制結果，特征諧波的頻率滿足2v±1的關系。其中，v＝1，2，…，∞。式(7)中第2、3、…項為一系列電壓調制波之和，其為整流開關函數對整流器輸出調制波電壓的調制結果。

此外，式(7)表明對于頻率為f_k的直流電壓波動分量，其會在基波和各特征諧波附近引起等幅成對的頻率成份，即n·f_m±f_k。伴隨特征諧波次數、幅值的變化，調制波幅值將隨之變化，考慮牽引網電壓以工頻為主，因而，對工頻作用的調制信號主導影響網壓幅值不穩定。對比式(3)、(7)可發現，兩式具有高度統一性，式(3)僅是式(7)的一個特例，驗證了本方法的實用性。

下面對本發明方法進行更詳細的闡述。

1)、使用DFT變換分析牽引網網壓各時間段主導頻率能量幅值分布，如表1所示。

表1 各時間段主導頻率能量幅值分布

2)、通過TLS-ESPRIT構造矩陣、擬合系數計算模式的幅值和初相位，并進行主導模式篩選。隨后采用頻率比對的方式，確定信號的模態成份，如表2所示。

表2 TLS-ESPRIT算法分析的牽引網電壓模態

3)、描述網壓頻率信號與整流器中間直流電壓頻率成份存在數學關系，如式(3)所示。

4)、考慮該現象中高次諧波成份也出現被調制現象，構造電壓波動信號，如式(4)所示。

5)、結合調制理論分析調制信號在HXD型電力列車整流器中傳播機理，該推導出的公式能夠反映工頻作用的調制信號主導影響網壓幅值不穩定現象。

6)、再無補償裝置的情況下，分析多車接入牽引網引發的電氣量波動規律，驗證本發明的實用性。