本發明涉及永磁同步電機相關技術領域，尤其是指一種基于曲線擬合的最大轉矩電流控制方法。

背景技術：

節能高效，對于凸極永磁同步電機而言具體表現在：節約成本、提高效率。要達到這些目標，不僅對電機的設計以及加工工藝提出了更高的標準，同時對于電機控制系統更是提出了很高的要求。目前最大轉矩/電流控制方法的實現主要有查表法和線性簡化法。查表法雖然實現了系統電流的最大利用率，但其控制精度受表中數據量大小的影響，要想得到高的精度就必須有大量的離散點，而這又會影響到整個系統的響應速度，但由于實現的方法以及控制所需存儲的查詢數據量大且離散、對于電機參數依賴性比較大、控制精度等弊端，在后續改進上存在很大空間。因此該方法的應用前景還是很客觀的。

中國專利申請公開號：CN 104167965A，申請公開日2014年11月26日，公開了一種永磁同步電機最大轉矩電流比控制方法，它是根據最大轉矩電流比控制對速度外環輸出的電流總的給定進行分配，通過對永磁同步電機的轉矩公式推算，再通過MATLAB軟件工具進行線性化，獲得d軸的電流給定和q軸的電流給定進行優化最大轉矩電流比控制，實現永磁同步電機恒轉矩區的優化控制。該發明的不足之處在于，控制精度受其表中數據大小的影響，同時控制的復雜程度高，系統的性能低，還對電機本體的參數存在依賴。

技術實現要素：

本發明是為了克服現有技術中存在上述的不足，提供了一種提高運算速度且提高系統性能的基于曲線擬合的最大轉矩電流控制方法。

為了實現上述目的，本發明采用以下技術方案：

一種基于曲線擬合的最大轉矩電流控制方法，具體包括如下步驟：

(1)根據矢量控制原理，將電機的電磁轉矩方程進行簡化，在穩態情況下，電機d軸和q軸的電流分量為常值；

(2)應用牛頓迭代法展開上述方程，從而獲得偏導矩陣，再設置一個收斂條件；

(3)在Matlab中運用數值分析方法得到電磁轉矩與電流d軸分量函數的對應曲線關系，其曲線接近為二次曲線的單支，對上述曲線進行等效三段二次曲線的合成，采用最小二乘法對其進行模擬逼近；

(4)將電磁轉矩與定子電流d軸分量建立成連續的函數關系，能夠快速輸出d軸分量。

本發明提出基于曲線擬合的最大轉矩電流控制，將迭代法用于求取最優解，并把得到的最優解通過數值分析的方法得到相應的曲線，然后對所得曲線用最高次數為2的數學函數進行擬合，用擬合后所得函數關系式替代傳統的查表法中大量的離散數據，從而簡化控制，消除了對于電機參數的依賴，對于任何給定的電磁轉矩都可以很快的計算出其對應的電流分量，節約了原系統的數據存儲量，提高了運算速度，改善系統性能，優化最大轉矩下的最小電流，提高電機控制系統效率。

作為優選，在步驟(1)中，電機的電磁轉矩方程簡化過程如下：

電機電磁轉矩方程為：

其中：P為電機極對數，為永磁體磁鏈，i_d和i_q分別為電機d軸和q軸的電流分量，L_d和L_q分別為電機d軸和q軸的電感分量，令i_s為電機總電流，則為最大轉矩電流控制的數學表達式如下：

其中，C_Tem為電機電磁轉矩值，上式表明最大轉矩電流控制在數學上就是求解一個二元函數的條件最小極值，采用拉格朗日函數法求解電流的極小值，構造拉格朗日極值函數為：

其中，λ_t為拉格朗日系數，令

可得

對上式化簡，消去拉格朗日系數λ_t有：

由此可見最大轉矩電流控制對電機參數的依賴很大，為了消除對電機參數的依賴，采用了以下整體換元對方程進行標幺化，令作為基值，對式(1)進行標幺化有：

其中：和分別為標幺化后電機d軸和q軸的電流分量，為標幺化后電機電磁轉矩值，當電機電磁轉矩C_Tem一旦確定，可由上式(2)確定相應電機d軸和q軸的電流極小值和此時標幺化后電機總電流最小，

其中：f_{min d}和f_{min q}分別為電機d軸和q軸的電流極小值函數。

由式(3)可以看出，電機d軸和q軸的電流分量i_d和i_q均為電磁轉矩Tem的函數，i_d和i_q電流值的獲得完全可以由其變量電磁轉矩Tem的取值獲得對應的函數值；從式(2)可以看出，電磁轉矩Tem與電機q軸的電流分量均為電機d軸電流分量的函數，故而若已知電機d軸的電流分量i_d便可求出對應的電機q軸的電流分量與電磁轉矩Tem，最終實現最大轉矩比電流控制的閉環控制。

作為優選，在步驟(2)中，應用牛頓迭代法展開上述方程，從而獲得偏導矩陣，具體操作步驟如下：

引入牛頓迭代法，將

展開成函數形式，則有：

從而可得式(4)的偏導矩陣為：

在式(5)中，假設在點處非奇異，則可用Newton法得到非線性方程組式(4)的解的迭代表達式：

式(6)中：

將式(4)、式(5)帶入到式(7)，可得：

作為優選，在步驟(2)中，為了提高解的精度，設定迭代的收斂條件為：

作為優選，在步驟(3)中，在Matlab中運用數值分析方法得到電磁轉矩與電流直軸分量函數的對應曲線關系，其曲線接近為二次曲線的單支，根據曲線特點，綜合考慮控制精度、運算復雜度將該曲線分成三段進行數學擬合，并且每個函數的最高次數為2，則有：

對于以上所構造的2次擬合曲線，為能求得精度盡可能高的解，可以采用最小二乘法對其進行模擬逼近。

作為優選，數據擬合的具體方法是：對給定數據點(x_i，y_i)(i＝0，1，…，m)，在取定的函數類型中求使誤差r_i＝f(x_i)-y_i(i＝0，1，…，m)的平方和最小，即

從幾何意義上說就是尋求與給定點(x_i，y_i)(i＝0，1，…，m)的距離的平方和最小的曲線f(x)，函數f(x)成為最小二乘解，求擬合函數f(x)的方法稱為擬合曲線的最小二乘法。

作為優選，在步驟(4)中，其采用最小二乘法對其進行模擬逼近后，為了將最大轉矩電流控制中電磁轉矩與電流d軸分量建立成連續的函數關系，設電流d軸分量為變量y，電磁轉矩為變量x，則有函數關系式：

y＝a₂x²+a₁x+a₀

設各數據差的平方和為：

上式中：x_i、y_i分別為對應的電磁轉矩Tem^*和電流d軸分量為使曲線擬合的精度更高，必須保證每個差的絕對值都很小，從而有：

整理后得到：

上式中可得：

從而有：

把式(6)迭代公式求出的Tem^*和數據點代入式(8)中，便可求出a₂、a₁、a₀，得到函數表達式。

作為優選，在式(8)中，的取值范圍為(-1，0)。

本發明的有益效果是：用擬合后所得函數關系式替代傳統的查表法中大量的離散數據，從而簡化控制，消除了對于電機參數的依賴，對于任何給定的電磁轉矩都可以很快的計算出其對應的電流分量，節約了原系統的數據存儲量，提高了運算速度，改善系統性能，優化最大轉矩下的最小電流，提高電機控制系統效率。

附圖說明

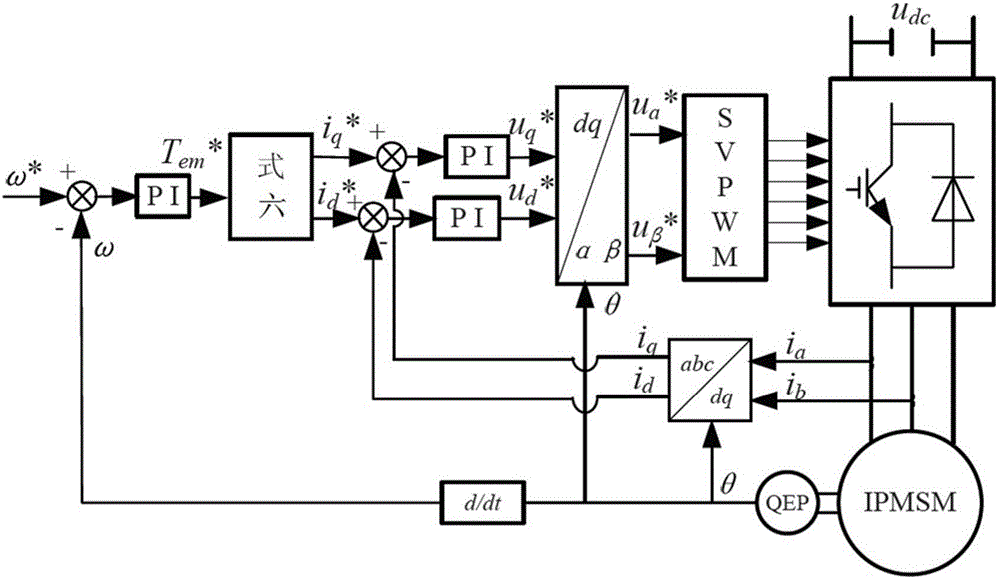
圖1是本發明的系統框圖。

具體實施方式

下面結合附圖和具體實施方式對本發明做進一步的描述。

如圖1所述的實施例中，一種基于曲線擬合的最大轉矩電流控制方法，根據矢量控制原理，將電機的電磁轉矩方程進行簡化，在穩態情況下，電機d軸和q軸的電流分量為常值，應用牛頓迭代法展開上述方程，從而獲得偏導矩陣，再設置一個收斂條件，在Matlab中運用數值分析方法得到電磁轉矩與電流d軸分量函數的對應曲線關系，其曲線接近為二次曲線的單支，對其進行等效三段二次曲線的合成，采用最小二乘法對其進行模擬逼近，經過以上步驟后，將電磁轉矩與定子電流d軸分量建立成連續的函數關系，能夠快速輸出d軸分量。

將迭代法用于求取最優解，并把得到的最優解通過數值分析的方法得到相應的關系曲線，然后對所得的關系曲線用最高次數為2的數學函數進行擬合，用擬合所得的函數關系式替代傳統的查表法中大量的離散數據，簡化了控制，提高了系統的性能。最大轉矩電流控制主要是運行在額定轉速以下即恒轉矩區域，在電機負載轉矩一定的條件下，使定子電流最小的電機控制方法，也稱作單位電流輸出最大轉矩的控制。凸極永磁同步電動機用得較多的一種電流控制策略就是最大轉矩電流控制，然而對于隱極永磁同步電動機，最大轉矩電流控制就是i_d＝0控制。

永磁同步電機的電磁轉矩方程：

其中：P為電機極對數，為永磁體磁鏈，i_d和i_q分別為電機d軸和q軸的電流分量，L_d和L_q分別為電機d軸和q軸的電感分量，令i_s為電機總電流，則為最大轉矩電流控制的數學表達式如下：

其中，C_Tem為電機電磁轉矩值，上式表明最大轉矩電流控制在數學上就是求解一個二元函數的條件最小極值，采用拉格朗日函數法求解電流的極小值，構造拉格朗日極值函數為：

其中，λ_t為拉格朗日系數，令

可得

對上式化簡，消去拉格朗日系數λ_t有：

由此可見最大轉矩電流控制對電機參數的依賴很大，為了消除對電機參數的依賴，采用了以下整體換元對方程進行標幺化，令作為基值，對式(1)進行標幺化有：

其中：和分別為標幺化后電機d軸和q軸的電流分量，為標幺化后電機電磁轉矩值，當電機電磁轉矩C_Tem一旦確定，可由上式(2)確定相應電機d軸和q軸的電流極小值和此時標幺化后電機總電流最小，

其中：f_{min d}和f_minq分別為電機d軸和q軸的電流極小值函數。

由矢量控制系統知識得知，在轉速閉環控制中轉速環的輸出為電磁轉矩給定值，然而由式(3)可以看出，雖然電機d軸和q軸的電流分量i_d和i_q均為電磁轉矩Tem的函數，故而，i_d和i_q電流值的獲得完全可以由其變量電磁轉矩Tem的取值獲得對應的函數值。然而它們之間并非線性關系，同時由于當前芯片計算能力的局限性，很難直接通過電磁轉矩的給定值而求出d軸、q軸的電流分量值，這就迫使我們必須通過其它方式對電流分量與電磁轉矩Tem之間的關系式進行簡化。

從式(2)以看出，電磁轉矩Tem與電機q軸的電流分量均為電機d軸電流分量的函數，從這一角度出發，只要已知直軸電流i_d便可求出對應的電機q軸的電流分量與電磁轉矩Tem，可實現最大轉矩比電流控制的閉環控制。現在最常用的方法是：將i_d、i_q、Tem之間的數據關系列成表格，通過查詢法便可依次查出轉速環輸出電磁轉矩分別對應的定子電流各分軸電流值并將其作為電流給定值，最終實現最大轉矩比電流控制的閉環控制。

引入牛頓迭代法，將

展開成函數形式，則有：

從而可得式(4)的偏導矩陣為：

在式(5)中，假設在點處非奇異，則可用Newton法得到非線性方程組式(4)的解的迭代表達式：

式(6)中：

將式(4)、式(5)帶入到式(7)，可得：

為了提高解的精度，設定迭代的收斂條件為：

在Matlab中運用數值分析方法得到了電磁轉矩與電流d軸分量函數對應的曲線關系。

實際電磁轉矩Tem^*與電流d軸分量的曲線圖近似為一二次曲線的單支。然又并不是標準二次曲線關，為了提高曲線精度，方便實現，將等效為三段二次曲線的合成。

其實電磁轉矩與d軸電流之間的關系并不是線性的。如果只用一個高次函數對其進行描述，得到的近似曲線與原曲線的擬合度不是很高，同時也為了便于實現(例如DSP)，因此需要對關系曲線進行分段數學擬合。根據曲線特點，綜合考慮控制精度、運算復雜度將該曲線分成三段進行數學擬合，并且每個函數的最高次數為2，則有：

對于以上所構造的2次擬合曲線，為能求得精度盡可能高的解，可以采用最小二乘法對其進行模擬逼近。數據擬合的具體方法是：對給定數據點(x_i，y_i)(i＝0，1，…，m)，在取定的函數類型中求使誤差r_i＝f(x_i)-y_i(i＝0，1，…，m)的平方和最小，即

從幾何意義上說就是尋求與給定點(x_i，y_i)(i＝0，1，…，m)的距離的平方和最小的曲線f(x)，函數f(x)成為擬合函數或最小二乘解，求擬合函數f(x)的方法稱為擬合曲線的最小二乘法。

為了將最大轉矩電流控制中電磁轉矩與電流d軸分量建立成連續的函數關系，設電流d軸分量為變量y，電磁轉矩為變量x，則有函數關系式：

y＝a₂x²+a₁x+a₀

設各數據差的平方和為：

上式中：x_i、y_i分別為對應的電磁轉矩Tem^*和電流d軸分量為使曲線擬合的精度更高，必須保證每個差的絕對值都很小，從而有：

整理后得到：

上式中可得：

從而有：

把式(6)迭代公式求出的Tem^*和數據點代入式(8)中，的取值范圍為(-1，0)，便可求出a₂、a₁、a₀，得到函數表達式。

從表達式中很直觀的看出對于給定任何一個電磁轉矩Tem可以很快的計算出所對應電流分量。用這個擬合的分段函數關系式替代傳統的查表運算，不但節約了系統的儲存量，還提高了系統的運算速度。