本發明涉及一種有源電力濾波器rbf雙神經網絡自適應滑模控制方法。

背景技術：

隨著社會的進步和發展，人們的生活水平日益提高，大量的用電設備投入到日常的生產生活中，隨之而來的就是，電網中出現大量的諧波和無功功率的污染，這嚴重影響著電能的質量。電網中存在諧波電壓或諧波電流會增加電力系統設備的附加損耗，導致測量和自動控制儀器失靈等問題，影響了設備的使用效率，嚴重時可能會因線路過熱引起火災。

目前主要采用外部諧波補償裝置來補償諧波，濾波器分為無源濾波器和有源濾波器兩種。無源濾波器對諧波的控制效果受系統的阻抗特性影響很大，極易受到溫度、諧波和非線性負載變化的影響，其濾波性能不穩定。除此之外，無源濾波器只能濾除特定階次的諧波，因此并不適用于諧波情況復雜的場所。存在只能補償特定諧波等缺陷，所以現在對電能問題的治理主要集中在有源濾波器。相比于無源濾波器，有源濾波器實現了動態補償，響應速度快；所需儲能元件容量不大；受電網阻抗的影響不大，不會和電網阻抗發生諧振等。

目前，國內外尚未形成系統的有源電力濾波器的先進控制理論體系，有源濾波器的建模方法因人而異，采用的控制方法也多種多樣，導致系統的穩定性和可靠性較低。

技術實現要素：

為解決現有技術的不足，本發明的目的在于提供一種有源電力濾波器rbf雙神經網絡自適應滑模控制方法，能夠對指令電流實時跟蹤補償、可靠性高、對參數變化魯棒性高、穩定性高。

為了實現上述目標，本發明采用如下的技術方案：

一種有源電力濾波器rbf雙神經網絡自適應滑模控制方法，其特征是，包括如下步驟：

步驟1)建立有源電力濾波器的數學模型；

步驟2)基于分數階滑模面設計自適應rbf雙神經網絡，利用兩個rbf神經

網絡分別逼近系統的非線性函數和干擾上界；

步驟3)根據分數階rbf雙神經網絡滑模控制器控制有源電力濾波器。

進一步地，所述步驟1)中數學模型的建立針對三相三線制系統有源電力濾波器。

進一步地，所述步驟1)中數學模型為其中，v1、v2、v3分別為電網與apf連接處的電壓，i1、i2、i3分別為apf注入電網的補償電流，lc為電感，rc為電阻，v1m、v2m、v3m、vmn分別為m點到a、b、c、n點的電壓。

進一步地，為了標識igbt的開關狀況，對步驟1)的模型進行形勢變換：

假設v1+v2+v3＝0,i1+i2+i3＝0，進而可以得到引入函數其中，k＝1,2,3；

由vkm＝ckvdc，將模型變換為：

進一步地，所述步驟2)中分數階滑模面為s＝-λ1e-λ2∫e-λ3d^α-1e，λ1,λ2,λ3為正常數，e表示跟蹤誤差；

基于分數階滑模面得到lyapunov函數v1、v2，式中s是切換函數，s^t為s的轉置，和分別是rbf雙神經網絡權值誤差，為的轉置，為的轉置，ω1^*和ω2^*分別為rbf雙神經網絡的理想權值，和分別為rbf雙神經網絡的實時估計權值，η1和η2分別為正常數；tr(·)表示對矩陣的主對角線上的元素求和；

根據lyapunov穩定性定理設計雙神經網絡的自適應律。

進一步地，所述步驟2)中rbf雙神經網絡的自適應律為：其中，φ(x)＝[φ1(x),φ2(x)…φn(x)]^t為高斯基函數。

本發明所達到的有益效果：在基于分數階滑模的有源電力濾波器自適應rbf雙神經網絡控制法中，分數階滑模面能夠不依賴于系統函數本身，快速的實現跟蹤；自適應rbf雙神經網絡控制器分別用來逼近有源電力濾波器中的非線性部分和干擾值的上界。設計的控制器能夠確保對指令電流的實時跟蹤并加強系統的魯棒性；可對有源電力濾波器進行有效、可靠的控制，在對系統參數未知的情況下，可以有效估計出系統的各項參數，并且保證系統全局的穩定性；在基于分數階滑模的有源電力濾波器自適應rbf雙神經網絡控制器的設計的基礎上，可逐步得到動態控制律和自適應律；在滑模控制的設計中主要是利用常規的滑模變結構控制，其能夠克服系統的不確定性，對干擾具有很強的魯棒性，尤其對非線性系統的控制具有很強的控制效果。

附圖說明

圖1是本發明具體實施例中有源電力濾波器的模型示意圖；

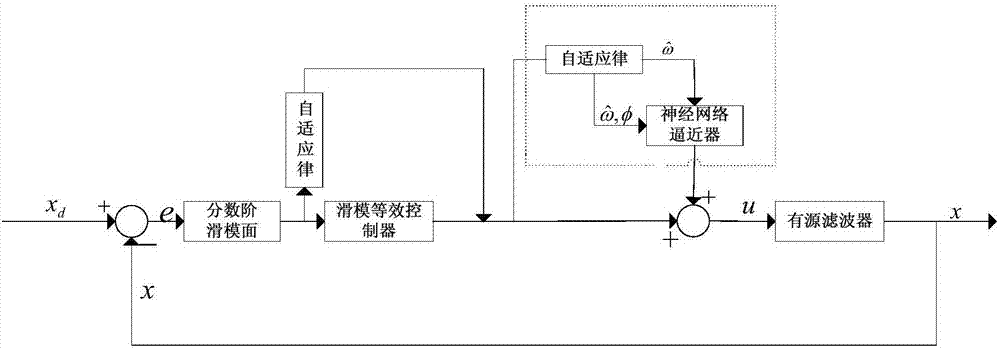
圖2是本發明的原理示意圖；

圖3是本發明的具體實施例中對電網電流進行補償之后的時域響應曲線圖；

圖4是本發明的具體實施例中對進行補償之后的電流頻譜圖。

具體實施方式

下面結合附圖對本發明作進一步描述。以下實施例僅用于更加清楚地說明本發明的技術方案，而不能以此來限制本發明的保護范圍。

本專利中一階導數的表示均采用的是字母上加點的形式。

本發明涉及一種有源電力濾波器rbf雙神經網絡自適應滑模控制方法，其特征是，包括如下步驟：

步驟1)建立有源電力濾波器的數學模型，本實施例中數學模型的建立針對三相三線制系統有源電力濾波器，其原因在于在生活中，三相交流電的應用占多數，所以主要研究用于三相三線制系統的情況。

主電路結構如圖1所示。有源電力濾波器的基本工作原理是，通過對電網電流進行實時采集，快速獲取相關的補償分量，經過對高性能變流器的控制，產生pwm波并且注入至有源電力濾波器中，產生相應的補償電流，進而消除諧波電流。

根據電路理論和基爾霍夫定理可以得到模型為其中，v1、v2、v3分別為電網與apf連接處的電壓，i1、i2、i3分別為apf注入電網的補償電流，lc為電感，rc為電阻，v1m、v2m、v3m、vmn分別為m點到a、b、c、n點的電壓。

假設v1+v2+v3＝0,i1+i2+i3＝0，進而可以得到

為了標識igbt的開關狀況，引入函數其中，k＝1,2,3；

由vkm＝ckvdc，將模型變換為：

由于在濾波器的主電路中，三相電路之間不存在耦合，因此，上述數學模型，可以視作三個相同結構的單相電路的物理組合，表示如下：其中x為apf注入電網的補償電流，x＝[i1i2i3]，是x的一階導數，非線性函數vdc是直流側電容電壓，d是未知干擾，滿足ρ-|d|＞σ1，σ1是一小正數，ρ是一正數，v1,v2,v3分別為apf主電路的電壓，rc為電阻，lc為電感。

步驟2)基于分數階滑模面設計自適應rbf雙神經網絡，利用兩個rbf神經網絡分別逼近系統的非線性函數和干擾上界。

具體地，利用分數階微積分設計滑模面，將滑模面中誤差的微分和積分階次從整數變化成分數；利用rbf神經網絡來逼近有源電力濾波器的非線性部和干擾值的上界，從而保證系統的穩定性。控制系統結構框圖如圖2所示。

本實施例中分數階滑模面定義為s＝-λ1e-λ2∫e-λ3d^α-1e，其中，λ1,λ2,λ3為正常數。基于分數階滑模面得到lyapunov函數v1、v2，式中s是切換函數，s^t為s的轉置，和分別是rbf雙神經網絡權值誤差，為的轉置，為的轉置，ω1^*和ω2^*分別為rbf雙神經網絡的理想權值，和分別為rbf雙神經網絡的實時估計權值，η1和η2分別為正常數。

根據lyapunov穩定性定理設計雙神經網絡的自適應律，rbf雙神經網絡的自適應律為：其中，φ(x)＝[φ1(x),φ2(x)…φn(x)]^t為高斯基函數，，其中，φi(x)是高斯函數，且現有技術中有如下形式根據三相數學模型可知，這里n＝3。

為了便于凸顯步驟2)中相關函數的設計原理，并且對于本發明可行性的證明，下面結合實施例就步驟2)的函數的選用以及設計進行說明：

考慮簡化后的apf系統：

假設1.系統干擾存在上界，并假設上界為ρ，ρ為正數。

系統干擾d和干擾上界ρ滿足不等式ρ-|d|≥σ1，σ1為小正數。

假設2.系統的非線性函數存在上界，并假設上界為fn(x)，fn(x)為正數。

系統非線性函數f(x)和上界fn(x)滿足不等式fn(x)-|f(x)|≥σ2，σ2為小正數。

定義跟蹤誤差為e＝xd-x(2-2)

跟蹤誤差的導數為

將系統模型(2-1)帶入(2-3)得

對于跟蹤控制問題，一般通過對跟蹤誤差進行線性組合設計滑模面，這里運用分數階微積分，定義滑模面s＝-λ1e-λ2∫e-λ3d^α-1e(2-5)

對分數階滑模面進行求導，得其中，λ1,λ2,λ3為正常數。

令滑模面的導數得

可求得等效滑模控制器：

根據以上求得的結論，可設計apf控制系統中，等效滑模控制律為：

表示符號函數，其表達式為：

在被控系統2-6中存在外界干擾的情況下，如果干擾有界，那么被控系統在等效控制律2-14的作用下能夠保持穩定，系統的跟蹤誤差都會收斂至0.

穩定性證明：

設計lyapunov函數為

對其進行求導，得

將等效控制律(2-9)帶入(2-12)，整理可得：

由假設1和2可知

因此，可以發現，在(2-9)的等效控制律的控制下，系統是全局漸進穩定。

在實際情況中，系統的非線性函數和未知干擾的上界很難得到，即非線性函數和干擾上界為一未知量。通常較為保守的做法為，取fn(x)和ρ為一個較大的值，然而較大值會引起控制力中很嚴重的抖振現象，可以采用兩個神經網絡來分別對上界值進行估計，與傳統取較大上界值的做法相比，可以大大減輕抖振現象。

根據假設1可知，

假設上界估計值設為利用第一個神經網絡對干擾上界估計值進行逼近可以表示為：

其中，是rbf神經網絡實時權值，是高斯函數，

同時，另設非線性函數上界估計為利用第二個神經網絡對其上界進行逼近，可以表示為：其中，是rbf神經網絡實時權值，是高斯函數。

假設3.假設在使用第一個神經網絡逼近干擾上界ρ時，存在最優權值ω^*1，滿足ω1^*tφ1-ρ＝σ3，σ3為干擾上界的逼近誤差，并且逼近誤差是有界的，即滿足|σ3|＜σ*，σ*為一正數。

假設4.假設在使用第二個神經網絡逼近非線性函數上界fn(x)時，存在最有權值ω^*2，滿足ω1^*tφ1-ρ＝σ4,σ4為非線性函數上界的逼近誤差，并且逼近誤差是有界的，即滿足|σ4|＜σ*′，σ*′為一小正數。

假設5.假設ρ，|d|，σ3，σ*滿足ρ-|d|≥σ3＞σ*；并且，fn(x)，|f(x)|，σ4，σ*′滿足fn(x)-|f(x)|＞σ4＞σ*′。

定義第一個神經網絡權值誤差為

定義第二個神經網絡權值誤差為

因此，可以利用雙神經網絡對非線性函數上界和干擾上界進行估計，將上界估計值(2-18)和(2-19)代入到控制力(2-9)中，可以得到改進的控制律為

切換項增益為使用神經網絡估計的干擾上界值和

在被控系統(2-1)中存在外界干擾的情況下，如果干擾有界，那么被控系統在控制力(2-22)的作用下能夠保持穩定，系統的跟蹤誤差都會收斂至0。控制力中魯棒項增益能夠通過自適應規律，根據系統跟蹤誤差自動調整。

穩定性證明：

設計lyapunov函數為

其中η為正數。

對(2-21)求導，并將(2-20)代入，可得

由于權值誤差為而最優權值ω1^*為固定值，因此

設計雙神經網絡權值自適應律為

代入(2-21),由假設3和假設4可得

因此，所設計的控制器能夠保證lyapunov函數的導數是半負定的；根據lyapunov穩定性第二方法，可以判定系統的穩定性。

步驟3)根據分數階rbf雙神經網絡滑模控制器控制有源電力濾波器。

實施例：

結合有源電力濾波器的動態模型和分數階滑模控制的自適應rbf雙神經網絡控制器的設計方法，通過matlab/simulink軟件設計出主程序。

設計的分數階滑模控制器參數λ1＝50,λ2＝10,λ1＝1，自適應參數取η1＝100,η2＝100，分數階α＝0.85，rbf神經網絡隱藏節點數為6。電源電壓vs1＝vs2＝vs3＝220v,f＝50hz。非線性負載的電阻40ω，電感5mh。補償電路電感10mh，電容100μf。

0.04s(s代表秒)時補償電路接入開關閉合，有源濾波器開始工作，并在0.1s和0.2s時接入一個相同的額外的非線性負載。

實驗的結果如圖3、圖4所示。圖3是電網電流進行補償之后的時域響應曲線圖，我們可以看到當有源電力濾波器開始工作以后，電流在0.05s就迅速接近正弦波,0.1s和0.2s增加負載以后,電流也能達到很好的響應速度,最后穩定在正弦波。從圖4，可以看出0.12s時,電流諧波的畸變率從0s的27.14％變為1.38％。

因此采用自適應分數階滑模rbf雙神經網絡控制的補償電流控制方法的有源電力濾波器不僅能很好的消除由非線性負載產生的諧波，并且穩定性也滿足了較高的要求。

本發明應用于有源電力濾波器的基于模糊滑模控制的自適應rbf神經網絡控制方法，該方法對有源電力濾波器進行有效、可靠的控制，在對系統參數未知的情況下，可以有效估計出系統的各項參數，并且保證系統全局的穩定性；在基于模糊滑模的有源電力濾波器自適應rbf神經網絡控制器的設計的基礎上，可逐步得到動態控制律和自適應律；在滑模控制的設計中主要是利用常規的滑模變結構控制，其能夠克服系統的不確定性，對干擾具有很強的魯棒性，對非線性系統具有很強的控制效果；自適應rbf神經網絡控制器用來逼近有源電力濾波器中的非線性部分。自適應模糊控制器能夠確保對指令電流的實時跟蹤并加強系統的魯棒性。本發明能夠確保對指令電流的實時跟蹤，并且加強系統的動態性能，提高系統魯棒性以及對參數變化不敏感。

以上所述僅是本發明的優選實施方式，應當指出，對于本技術領域的普通技術人員來說，在不脫離本發明技術原理的前提下，還可以做出若干改進和變形，這些改進和變形也應視為本發明的保護范圍。