本發明涉及微電網領域，尤其是一種微電網線性化潮流計算方法。

背景技術：

微電網是有多種分布式電源(distributedgeneration,dg)、配電線路以及負荷構成的中低壓電力系統，它的穩態模型是潮流方程。而潮流方程的計算是微電網的系統規劃、經濟調度、狀態估計、電壓控制等應用技術的基礎。因此，對微電網潮流方程的建模、分析與計算，是微電網最重要的科研工作之一。

為大量消納可再生能源，同時提高用戶電能質量，大量微電網控制策略被提出，如今形成了以分層控制為標準，多控制器之間相互協調的體系。微電網內部的控制系統分為兩層，一次控制是微電源控制器采用本地信息來迅速調節dg出力，保持系統電壓和頻率穩定，一般采用各種下垂控制策略；二次控制用來調節一次控制所產生的靜差，根據通訊條件不同分為集中式、分散式和分布式三大類。現有的方法根據控制策略的不同將微電網潮流計算進行分類，并將控制策略的具體模型帶入非線性潮流方程中考慮。然而，這一做法導致：

1)當逆變器數量較多時，將大幅增加方程的維數，而且需要對不同的控制策略進行單獨建模，增加了問題的復雜程度。

2)非線性交流潮流方程的各狀態變量高度耦合，需要依賴數值迭代方法求解。然而，迭代方法計算效率較低，而且收斂性難以保證，無法微電網的在線應用，如實時調度、靜態安全分析等對計算時間的要求。

由于線性方程組具有成熟的求解方法，不存在收斂性問題，且可以求得未知量的解析表達式。因此，將非線性潮流方程線性化是一種常用方法，典型的是廣泛應用于輸電系統的直流潮流。然而，直流潮流假設了所有母線電壓為常數、各相鄰節點間的相位差很小、忽略線路電阻以及無功功率。這些假設嚴重不符合較高的中低壓微電網工況，會導致較差。另外一個常用的潮流方程線性近似是配電網線性化支路潮流方程，即“lindistflow”，它假設系統中網絡為輻射狀拓撲，消去了電壓相角，且忽略了系統線路損耗。因此，該方法對微電網的拓撲結構做出了限制，求解各節點電壓相角，且在線路重載的情況下會產生較大的誤差。

綜上所述，現有的微電網非線性潮流計算方法難以保證計算的高效性和收斂的穩定性；而現有的線性化潮流計算方法無法保證結果的高精確性。

技術實現要素：

本發明提供一種微電網線性化潮流計算方法，對微電網控制系統所要達到的平衡點進行建模，大幅降低方程維度，并將非線性潮流方程線性化，提升計算結果的精確度。

一種微電網線性化潮流計算方法，包括如下步驟：

獲取微電網的網絡參數；

為各分布式電源dg成比例分配負荷功率，計算dg節點注入功率，具體為

其中，分別為dg注入節點i的不包含線損的有功功率估計值和無功功率估計值，plj、qlj分別為節點j的負荷功率，mi和ni分別為由dg的控制參數所決定的功率分配因子，ng、nl分別是微電網節點集合n＝{0,1，…，n}的電源節點和負荷節點子集合；

依據微電網在不同控制策略下所要達到的平衡點，建立如下微電網線性化潮流方程：

其中，δv為節點電壓偏移相量所組成的矢量，s為各節點注入復功率矢量，vn為微電網無負荷接入時的各節點電壓矢量；

依據所述線性化潮流方程計算接入負荷后節點電壓的偏移量、節點電壓幅值、節點電壓相角以及包含線損的dg輸出功率。

優選的，所述節點電壓的偏移量的計算過程具體為：

解析所述線性化潮流方程，依據下列計算式計算負荷接入后的節點電壓偏移相量：

其中，δe和δf分別為δv的實部和虛部矢量，en和fn分別為vn的實部和虛部矢量，i為n維單位矩陣，h、n、j和k為子矩陣。

優選的，所述子矩陣h、n、j和k的計算過程具體為：

建立如下矩陣：

dv＝diag(en)²-diag(fn)²

其中，為無負荷節點電壓幅值；

子矩陣h、n、j和k依據如下計算式獲得：

其中，*表示矩陣的hadamard積。

優選的，所述節點電壓幅值和節點電壓相角的計算過程具體為：

計算直角坐標系下的節點電壓相量：v＝vn+δv，式中，為各節點電壓相量所組成的矢量；

依據節點電壓相量計算節點電壓幅值：e＝en+δe，式中，為節點電壓幅值矢量，en＝[|vn1|,...,|vnn|]^t為無負荷電壓幅值矢量；

計算節點電壓相角：θ＝θn+δf，式中，θ節點電壓相角矢量，θn＝[θn1,...,θnn]^t為無負荷電壓相角矢量，其中各節點無負荷電壓相角的計算公式為：

優選的，所述獲取微電網的網絡參數的步驟具體包括：

讀取微電網的各網絡參數，生成節點導納矩陣y，將節點導納矩陣分解為

定義節點阻抗矩陣為

優選的，所述dg輸出功率的計算過程如下：

取出矩陣ym中所有dg節點所在的行，并按照dg節點在前，負荷節點在后的排列順序生成矩陣yg＝[ygg,ygl]，其中

dg輸出功率的計算式為：sg＝diag(vg)yggvg+diag(vg)yglvl；

其中，vg為dg節點電壓矢量，vl為負荷節點電壓矢量，sg為包含線損的dg輸出功率矢量。

優選的，所述無負荷接入時各節點電壓的計算式為：

vn＝zy0v0，式中，v0為pcc節點的電壓值。

本發明的有益效果是，本發明根據微電網不同控制策略所要達到的共同目的，依據控制系統的穩態平衡點進行建模，無需考慮微電源控制器的內部動態，大幅降低方程維數，簡化了建模。同時，將非線性潮流方程線性化，從而得到各未知量的解析表達式，僅需要求解線性方程組，即可得到，計算結果的精確度更高。

附圖說明

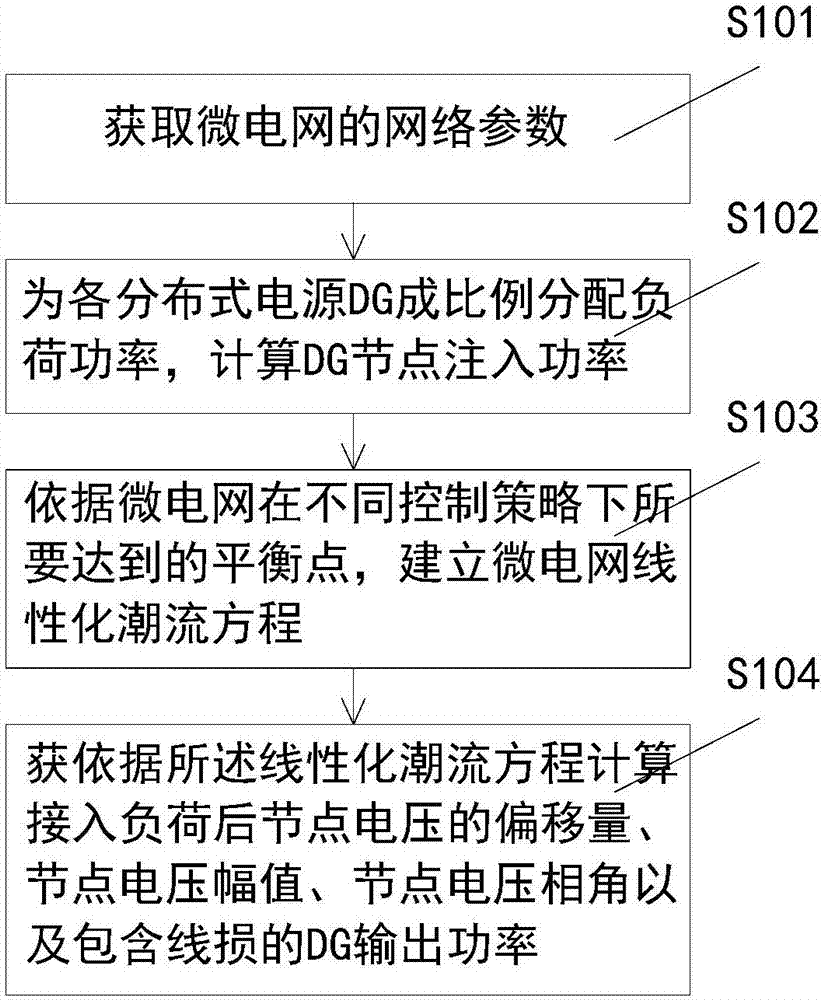
圖1為本發明一種實施例的微電網線性化潮流計算方法的流程圖；

圖2為本發明一種實施例的微電網的結構示意圖；

圖3為基礎負荷下的電壓幅值結果比較圖；

圖4為基礎負荷下的電壓相角結果比較圖；

圖5為2.5倍負荷下的電壓幅值結果比較圖；

圖6為2.5倍負荷下的電壓幅值結果比較圖。

具體實施方式

下面通過具體實施方式結合附圖對本發明作進一步詳細說明。

本發明實施例提供一種微電網線性化潮流計算方法，包括如下步驟：

s101：獲取微電網的網絡參數；

微電網的網絡參數是指為建立微電網線性化潮流方程所需的網絡參數，包括微電網的節點數量、節點電壓等，具體可以通過微電網內設置的各種傳感器獲得。

在獲取到各網絡參數后，可依據微電網的各網絡參數，生成節點導納矩陣y，將節點導納矩陣分解為

定義節點阻抗矩陣為

s102：為各分布式電源dg成比例分配負荷功率，計算dg節點注入功率；

將微電網不同控制策略所要達到的平衡點，即各dg成比例分配負荷功率，進行建模。微電網的一次、二次控制的目標在于將有功負荷、無功負荷在各dg之間成比例分配，有：

當不計線路損耗時，可以得出dg節點注入功率的估計值，具體為：

其中，分別為dg注入節點i的不包含線損的有功功率估計值和無功功率估計值，plj、qlj分別為節點j的負荷功率，mi和ni分別為由dg的控制參數所決定的功率分配因子，ng、nl分別是微電網節點集合n＝{0,1，…，n}的電源節點和負荷節點子集合。

s103：依據微電網在不同控制策略下所要達到的平衡點，建立微電網線性化潮流方程；

在傳統的高斯-賽德爾潮流計算方法中，非線性潮流方程可以寫成如下隱式z-bus形式：v＝zdiag(v)^-1s+zy0v0，此時，負荷接入后的節點電壓偏移相量為δv＝v-vn＝zdiag(vn+δv)^-1s，式中，δv為節點電壓偏移相量所組成的矢量；s為各節點注入復功率矢量。

當|δvi|＜1時，該式可以展開為如下諾依曼級數形式：

忽略式中高階項，得到如下形式的微電網線性化潮流方程：

其中，δv為節點電壓偏移相量所組成的矢量，s為各節點注入復功率矢量，vn為微電網無負荷接入時的各節點電壓矢量。

s104：依據所述線性化潮流方程計算接入負荷后節點電壓的偏移量、節點電壓幅值、節點電壓相角以及包含線損的dg輸出功率。

利用上述待求解參數與網絡參數間的線性關系，可通過解析表達式方式求解，所述節點電壓的偏移量的計算過程具體為：

解析所述線性化潮流方程，依據下列計算式計算負荷接入后的節點電壓偏移相量：

其中，δe和δf分別為δv的實部和虛部矢量，en和fn分別為vn的實部和虛部矢量，i為n維單位矩陣，h、n、j和k為子矩陣。

具體的，所述子矩陣h、n、j和k的計算過程具體為：

建立如下矩陣：

dv＝diag(en)²-diag(fn)²

其中，為無負荷節點電壓幅值；

子矩陣h、n、j和k依據如下計算式獲得：

其中，*表示矩陣的hadamard積。

節點電壓幅值和節點電壓相角的計算過程具體為：

計算直角坐標系下的節點電壓相量：v＝vn+δv，式中，為各節點電壓相量所組成的矢量；

依據節點電壓相量計算節點電壓幅值：e＝en+δe，式中，為節點電壓幅值矢量，en＝[|vn1|,...,|vnn|]^t為無負荷電壓幅值矢量；

計算節點電壓相角：θ＝θn+δf，式中，θ節點電壓相角矢量，θn＝[θn1,...,θnn]^t為無負荷電壓相角矢量，其中各節點無負荷電壓相角的計算公式為：

dg輸出功率的計算過程如下：

取出矩陣ym中所有dg節點所在的行，并按照dg節點在前，負荷節點在后的排列順序生成矩陣yg＝[ygg,ygl]，其中

dg輸出功率的計算式為：sg＝diag(vg)yggvg+diag(vg)yglvl；

其中，vg為dg節點電壓矢量，vl為負荷節點電壓矢量，sg為包含線損的dg輸出功率矢量。

其中，上述實施例中的無負荷接入時各節點電壓的計算方式可采用現有方法，在傳統的高斯-賽德爾潮流計算方法中，非線性潮流方程可以寫成如下隱式z-bus形式

v＝zdiag(v)^-1s+zy0v0

此時，無負荷節點電壓可由如下公式計算：vn＝zy0v0，式中，v0為pcc節點的電壓值。

至此，所有潮流計算中的待求量均可以由上述解析表達式經簡單的矩陣運算得出，且無需迭代，不存在收斂性問題。

本發明實施例可采用ieee-123節點三相配電網算例，選取其中一相并加入分布式電源進行計算，如圖2所示，網絡與負荷參數來自ieee下屬配電系統分析委員會提供的標準算例系統集。

本發明提出方法得到的節點電壓、相角與交流潮流方程、傳統直流潮流方程、以及配電系統線性支路潮流方程在給定負荷以及重載條件下的對比如圖3、圖4、圖5和圖6所示。從圖中的對比可知，本發明所提出的方法的計算精度均高于現有線性化潮流計算方法，而且在重載條件下依然可以給出高精度的計算結果。相對于精確模型依賴于數值迭代方法，本方法僅需要求解線性方程組，計算效率高且不存在收斂性問題。該方法對微電網在線監測、優化規劃、狀態估計以及控制算法設計等方面都有重要意義，具有廣泛的推廣應用前景。

以上內容是結合具體的實施方式對本發明所作的進一步詳細說明，不能認定本發明的具體實施只局限于這些說明。對于本發明所屬技術領域的普通技術人員來說，在不脫離本發明構思的前提下，還可以做出若干簡單推演或替換。